面向高校大类招生质量评估的跨尺度结构拓扑优化模型

李佩,，周涵，张睿，王克勤,，杨益新

（1.西北工业大学计算机学院，西安 710072；2.西北工业大学教务处，西安 710072；3.西北工业大学机电学院，西安 710072；4.西北工业大学管理学院，西安 710072；5.西北工业大学航海学院，西安 710072）

随着机械结构优化理论的不断成熟与发展，从宏观/细观/微观尺度上同时发掘材料的应用潜力，是提升结构性能、实现轻量化设计的重要方法[1-3]。机械结构跨尺度设计是以均匀化方法、多尺度有限元理论为纽带建立宏观尺度与微观尺度之间的性能映射，可同时对宏观结构和材料微观构型进行优化从而获得更高性能的结构构型[4-6]。Rodrigues等[7]利用多层级拓扑优化实现了宏观结构和材料微观构型串行设计，首先对宏观结构进行拓扑优化设计，然后以每个单元的密度值为材料体积用量约束，进而对每个单元单独进行微结构构型设计，实现了材料/结构的多尺度协同优化。Coelho等[8]将该方法拓展到三维结构中，但该方法中结构设计和材料设计相互独立，并未实现真正的协同优化。文献[9-10]分别基于密度法和水平集法提出了具有单一微结构的材料结构协同优化方法，这种方法为减小计算规模，保证结构可制造性，过度强调微观结构的一致性，难以充分发掘材料承载潜力。文献[11]基于FE2框架提出了更加自由的设计方法，宏观结构和空间各处的材料都能得到最优构型，但因设计变量数目庞大，计算效率比较低。随后又构建了简化的数据库模型，用显示近似的方法替代了重复的材料微结构拓扑优化设计，在较低的计算成本下设计出大规模、高精度的双尺度结构，但仍无法保证相邻微结构的连接性[12]。为解决这一问题，Wang 等[13-14]提出了基于参数化点阵的宏/微观协同优化方法，通过两类设计变量同步优化宏观材料分布和点阵构型变化，大幅降低了设计变量规模，保证了相邻微结构的连接性，并通过数值仿真和实验验证了梯度点阵结构比均匀点阵具有更优异的力学性能。

机械结构跨尺度拓扑优化的核心在于把合适属性的微结构放置在合适结构的合适位置上，达到最优性能。大类招生及培养工作与机械结构跨尺度优化设计类似，只有根据大类自身的发展情况招收具有合适大类基础的本科生并制定合适的培养方案，才能充分发掘学生的学习潜力，培养优质毕业生，促进一流学科的建设。因此，本工作在机械结构的跨尺度拓扑优化理论基础上，提出了高校大类招生质量评估量化模型，对学生个体数据（如入学成绩、报考大类和大类忠诚度）构建各向异性微结构量化的等效弹性矩阵表征代理模型及人工神经网络模型，同时以宏观结构应变能对大类整体发展建立量化模型，基于多尺度有限元技术建立了多尺度优化模型对大类招生进行优化分析。通过对大类招生工作质量评估，可客观认识所录取学生质量的差异性和学习潜力，进而对学生是否达到招生目标进行全局性量化，为制定和调整招生政策提供理论参考。

1 学生个体量化模型

随着大类招生、平行志愿和完全学分制的推广，各大类招生时不再局限本大类第一志愿学生，同时也要吸纳报考其他大类、不同考分段、不同大类诉求、甚至各类调转大类意向的学生，因此构建招生质量评估模型是评价招生政策优劣、保障招生-培养联动的重要基础。

招生工作中，学生个体属性包括入学成绩、报考大类和大类忠诚度，本文提出采用具有各向异性属性的微结构来表征每个学生个体，如图1所示。该微结构单胞由一个固定外框和一根可旋转变宽度的杆（蓝色区域）组成，其中微结构体分比（相对密度）可以等效表征学生入学成绩，入学成绩越高体分比越大、对应微结构力学性能越强。约定坐标轴x 方向代表本大类方向，蓝色杆方向代表报考第一志愿大类方向，因此二者之间夹角表明了本科大类与报考大类之间的相关性，当角度为零时，该微结构在方向上的力学性能最佳，意味着该学生在所报考大类具有更多优势，相反，随着该角度增大，报考大类的相关性就会越差。

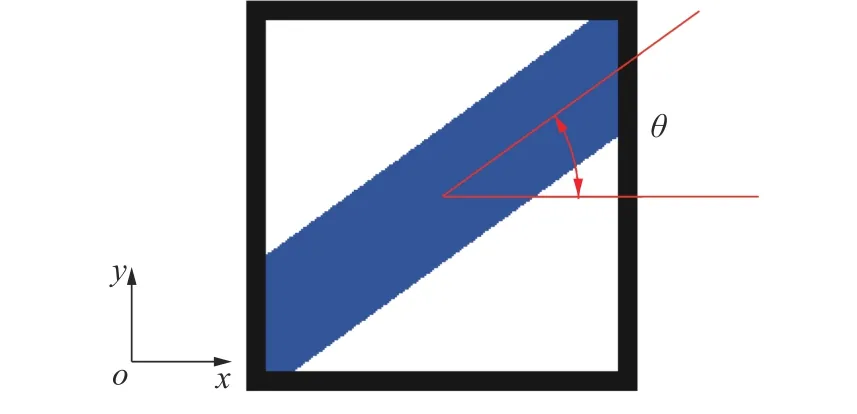
图1 学生个体量化微结构

作为学生个体，其量化微结构可通过两个参数来描述，一是微结构的体分比ρ，为学生的入学成绩，另一个是偏转角度θ，即大类相关性。通过改变两个控制参数得到一系列参数化微结构构型，如图2所示。

图2 参数化微结构构型随参数的演化规律

在微结构定义基础上，需要建立精确、合理、高效的微结构性能表征模型以关联微观结构参数与宏观结构性能。为了提高后期结构响应的计算效率，本文提出采用多尺度有限元技术将每个微结构看成一个超单元，与传统的有限元技术不同，多尺度有限元通过构造多尺度位移基函数来描述微结构内部的微观位移信息，而这种微观信息在进行宏观计算的时候不需要考虑，因此显著降低了模型复杂度。根据多尺度有限元理论，通过求解在微结构内部满足边界条件下的平衡方程来构造多尺度数值基函数：

式中：Ni为待求解的粗网格节点i 上的基函数；D为组成微结构基体材料的弹性矩阵；Ω 为微结构求解域。根据指定边界条件构造完所有节点的基函数后，微结构的等效刚度矩阵可以表达为

式中Ks为微结构的整体刚度矩阵。

在实际情况中，由于对本大类的主观认同性和兴趣方向的差异性，因此学生会有一定概率离开本大类，为描述这一情况，因此引入大类忠诚度的概念，即留在本大类不转走的概率，其具体的取值可以通过调查问卷等措施获得。对应到微结构中，该因素可以通过对刚度矩阵引入线性折减系数来衡量，因此新的微结构等效刚度矩阵可以改写为

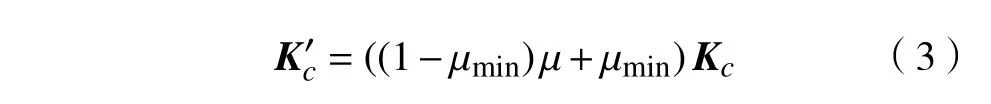
式中μmin为避免微结构刚度矩阵奇异而引入的最小折减系数，取值为0.01。

为了提高后续跨尺度优化模型的计算效率，避免重复构造多尺度数值基函数，基于人工神经网络建立微结构等效刚度的预测模型[15]。基于全试验设计方法进行均匀采样，选取N 个样本微结构并基于上述的多尺度有限元方法计算等效刚度矩阵，3种典型微结构及其等效刚度矩阵如图3所示。

图3 3种典型的微结构及其对应的等效刚度矩阵

对4节点二维单元来说，其刚度矩阵具有64个分量，将每个分量均作为神经网络的输出无疑会增加网络的规模，同时也会导致训练好的网络具有较大的误差。因此有必要对刚度矩阵进行降维处理，采用主成分分析方法提取出一组标准正交基，而微结构的等效刚度矩阵可以进一步表达为这组基矩阵的线性组合，组合系数即为等效刚度矩阵新形式，其分量个数会远远小于64。从样本规模、训练速度、拟合精度等多方面综合衡量，选择广义回归神经网络作为预测模型，该神经网络由输入层、模式层、求和层和输出层组成，其数学表达形式为

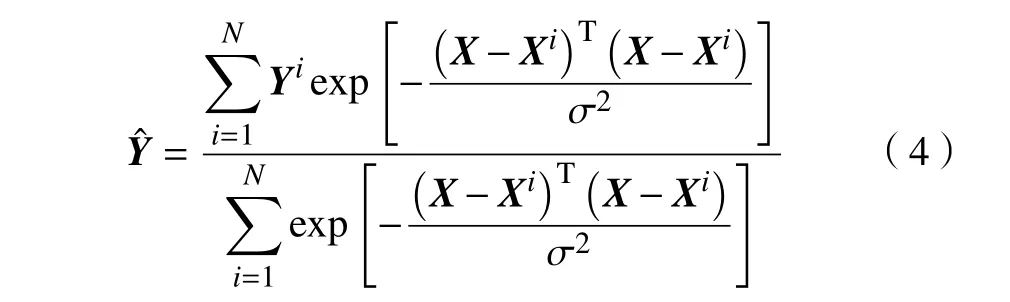
式中：X 为输入参数；Xi为模式层神经元对应的学习样本；σ 为光滑因子，其值越小拟合曲面越光滑，对应的训练误差也会增大，其值越大，虽有助于减小训练误差，但网络的泛化能力降低。为平衡训练误差和泛化能力，经过多次数值实验，将光滑因子设为1。

2 大类整体评估量化模型

基于上述建立的学生个体量化微结构模型，整体大类招生质量评估可以通过构建以不同属性微结构在宏观尺度布局为设计变量、以宏观结构整体应变能最小为目标的跨尺度结构拓扑优化设计模型来实现，该模型的数学表达形式为：

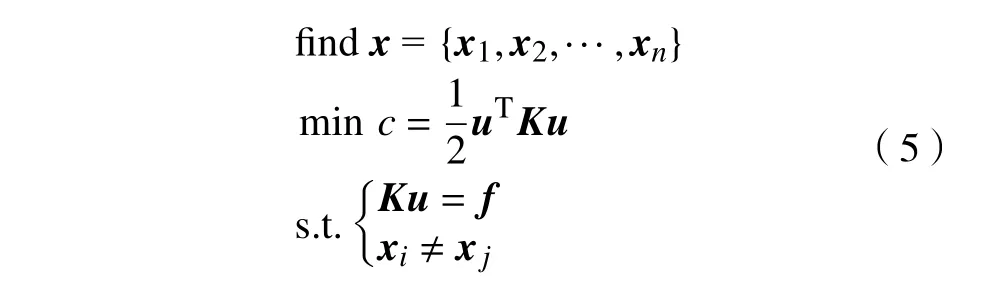
式中：x 为设计变量，包含所有微结构的位置，其中xi为第i 个微结构的坐标向量；c 为优化模型的目标函数应变能；Ku=f 为宏观结构的静力平衡方程；u和f 分别为结构位移向量和载荷向量；K 为整体结构刚度矩阵，由所有微结构刚度矩阵组装而成，而每个微结构的等效刚度矩阵可由式（3）和式（4）快速预测。

基于该模型对西北工业大学某大类的招生质量进行量化评估。近三年每年录取的285名考生情况如图4所示，按报考大类可以分为9类，其中1大类为本大类，随着大类编号的增加，报考的大类与本大类的相关性会逐渐降低。其中2019年在9个报考大类均招收了数量不等的考生，而在后两年为提升招生质量取消了大类9的招生。

图4 2019～ 2021年某大类招生情况

针对某大类招生质量评估建立的宏观设计域如图5所示，该设计域被离散为20×15个微结构单元，每个微结构单元尺寸为10 mm ×10 mm，在设计域左侧边界在x 方向固定，同时约束左侧边界下端点y 方向的自由度，在右侧边界施加线均布压力10 N/mm，便于压力载荷的施加，右侧添加10 mm 宽的非设计域。采用基于梯度信息的移动渐近线方法对微结构布局优化问题进行求解。

图5 宏观设计域

经过优化后，得到招收学生在描述大类的整体结构中分布情况，如图6所示。

图6 某大类2019年招收学生分布情况

对应的跨尺度结构和在相应载荷下位移分布如图7所示，微结构分布情况体现出良好的承载性能，招收学生分布合理，结构应变能为83.66 mJ。基于提出的模型对该大类在2020年和2021年的招生质量执行量化评估，得到相应的跨尺度结构和位移响应分布云图如图8和图9所示，同时对应的应变能分别为78.31 mJ 和77.55 m。

图7 2019年大类质量跨尺度结构模型与位移响应结果

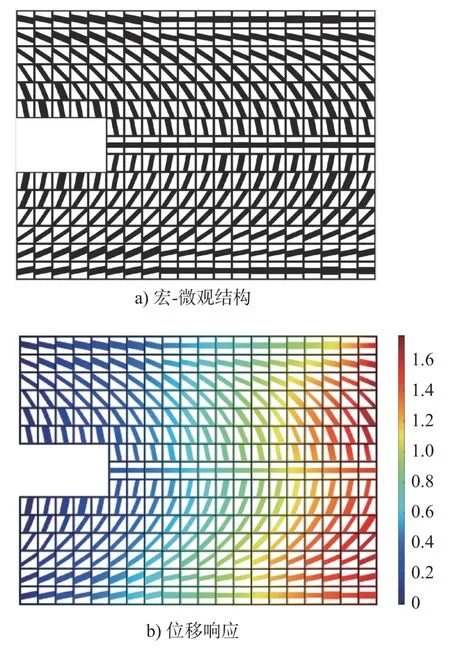
图8 2020年大类质量跨尺度结构模型与位移响应结果

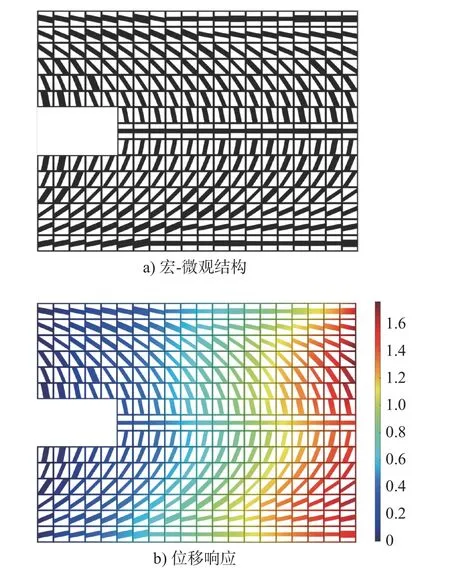
图9 2021年大类质量跨尺度结构模型与位移响应结果

由图8和图9可知，跨尺度结构具有更佳的机械性能，说明取消9大类学生招生后，招生质量显著提升，而后两年的招生质量差别不大。

3 结束语

本文基于机械结构跨尺度拓扑优化技术提出了高校大类招生评估量化模型，从学生个体和大类整体两个尺度出发，首先将个体入学成绩、入学报考大类和大类忠诚度这3个方面属性按照微结构体分比、微结构构造特征相关度、考虑构造缺陷的微结构性能折减进行建模；其次基于多尺度有限元方法和人工神经网络代理模型，对学生个体属性进行综合量化；最后构建了以不同属性微结构在宏观尺度布局为设计变量、以宏观结构整体应变能最小为目标的跨尺度结构拓扑优化设计模型，对高校大类招生质量的量化评估提供了有效的评估方法。