面向连续体结构拓扑优化的分区密度修正敏度过滤方法研究
2022-12-02张国锋徐雷王鑫李大双
张国锋,徐雷,王鑫,李大双
(四川大学 机械工程学院,成都 610065)
在现代科学、经济和工程应用中,优化显得尤 为重要。得益于计算机科学的迅猛发展,各种复杂的优化问题能够在有限元环境中通过数学模型及算法进行模拟和快速求解。连续体结构拓扑优化[1]已成为当前拓扑优化研究方向的热点问题之一,其在机械工程、土木工程、汽车轻量化等多领域具有普遍应用。目前,常用的拓扑优化方法是均匀化方法[2]、变密度法[3]、水平集方法[4]、渐进结构优化法[5]和ICM 方法[6]等。其中,变密度法因其设计变量少、程序简单及应用范围广等特点被广泛应用,其实质是单元密度为0 到1 的离散变量之间的排列组合的问题[7]。在优化过程中普遍存在如棋盘格现象、网格依赖性等数值不稳定的问题[8],制约了变密度法在结构拓扑优化领域的发展。
文献[9]提出一种考虑过滤半径的敏度过滤方法,有效解决棋盘格、网格依赖性等问题,当所设定的过滤半径较大时,拓扑优化边界会出现边界扩散等问题,使其直接制造性不强。为了获取清晰的拓扑优化边界,文献[10]在原有敏度过滤方法的基础上通过忽略密度项进行修正,但该方法存在迭代速度较慢,个别区域仍存在灰度单元的问题。诸多学者[11-12]通过引入Heaviside 函数的方法来控制边界扩散现象,但迭代次数较多,效率较低。国内学者对此也做了大量研究,罗震等[13]提出一种二重敏度过滤技术有效获得边界清晰的拓扑结构,但在过滤半径较小、单元数目较多时,优化结果会产生多余的细小结构。廉睿超等[14]提出一种考虑分区混合权重的敏度过滤方法,在网格划分数目较多时,能有效抑制细小结构的产生,但迭代速度较慢。此外,龙凯等[15]提出一种考虑密度梯度的敏度过滤方法,但个别条件下结构开孔数目发生变化,影响最终拓扑结果。张志飞等[16]提出一种双重SIMP 方法,但个别工况下仍存在灰度扩散现象。陈垂福等[17]提出一种变过滤半径的敏度过滤方法,但不能有效控制单元的最小尺寸。
针对Sigmund 敏度过滤方法中边界灰度问题,本文在现有研究的基础上提出了一种分区密度修正的敏度过滤方法,将原敏度过滤区域进行划分,采用新的复合卷积因子对不同区域处理,进一步自动判断单元敏度绝对差值大小,采用密度修正权值,有效弱化边界扩散的问题。该方法能有效获得边界清晰的拓扑优化结果,并保证了求解的稳定性,且提升迭代速度,降低柔度收敛值,提高结构刚度。本文以柔度最小化为优化目标,通过选取多个二维平面结构算例验证本文方法的可行性。
1 变密度法拓扑优化理论
拓扑优化是根据给定的负载及边界条件对特定的设计空间进行优化的一种数学梯度方法,利用最优准则算法求解拓扑优化问题,其目标是使系统柔度最小化。在连续体拓扑优化中,首先确定设计域及设计变量,将设计区域按需求划分为多个子区域,对其进行结构分析以满足预设优化条件。如图1 所示, ΩS为 实体区域, ΩV为空白区域,则设计域为Ω=ΩS+ΩV。
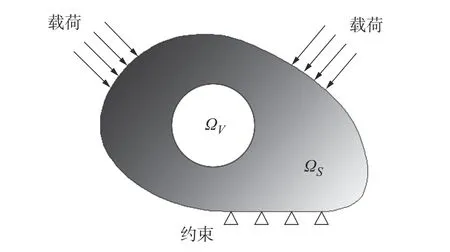
图1 设计域与单元密度
固体各向同性材料的惩罚法(Solid isotropic microstructures with penalization,SIMP)即变密度法主要用于处理中间密度,是目前主流的基于有限元的复合连续体拓扑优化方法。变密度法通常将元素相对密度作为设计变量,将0 到1 的整数优化问题转化为连续变量优化问题。
对于变密度方法,拓扑变量被映射到密度变量中。选用各向同性材料,建立变密度法插值模型的表达式定义为

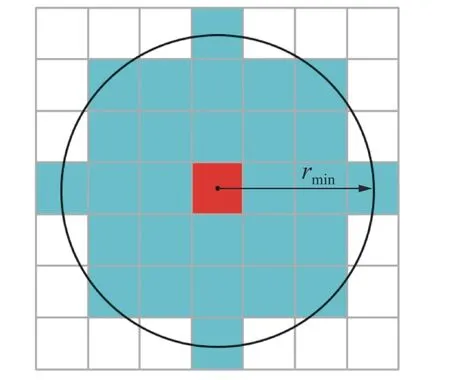
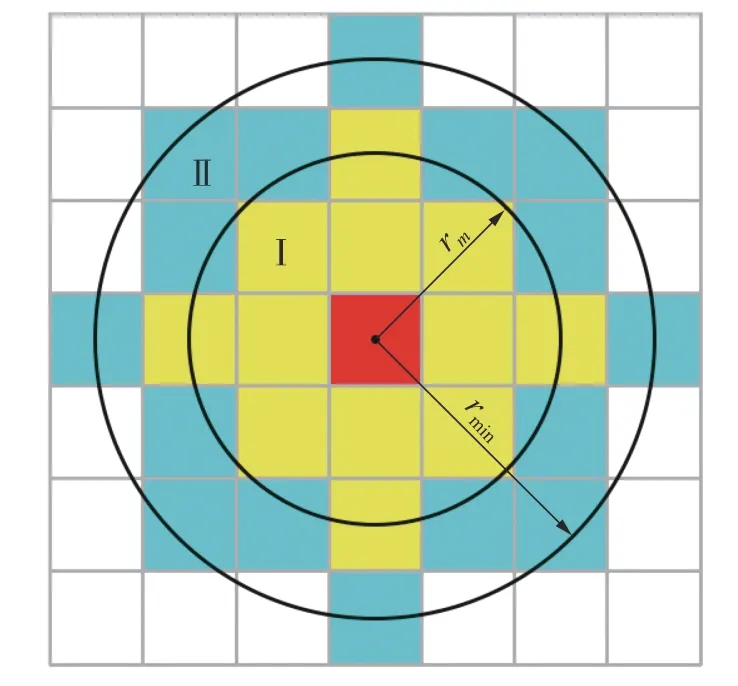
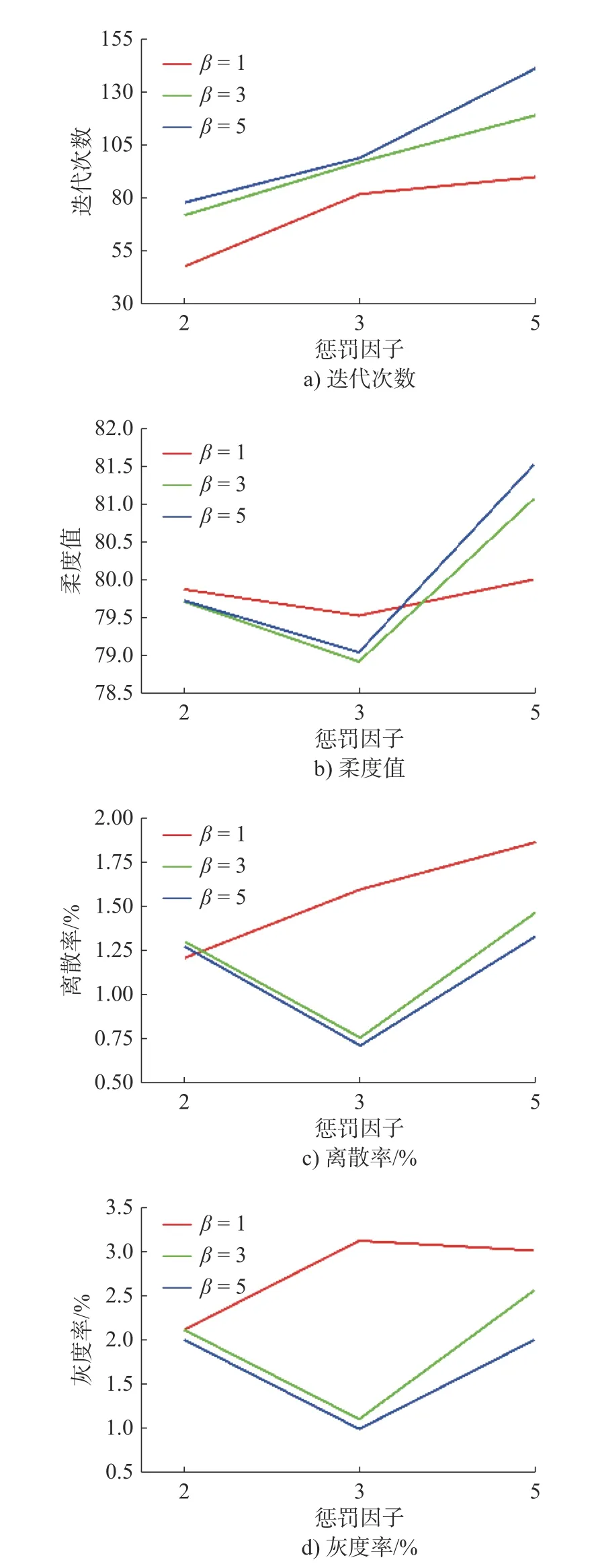
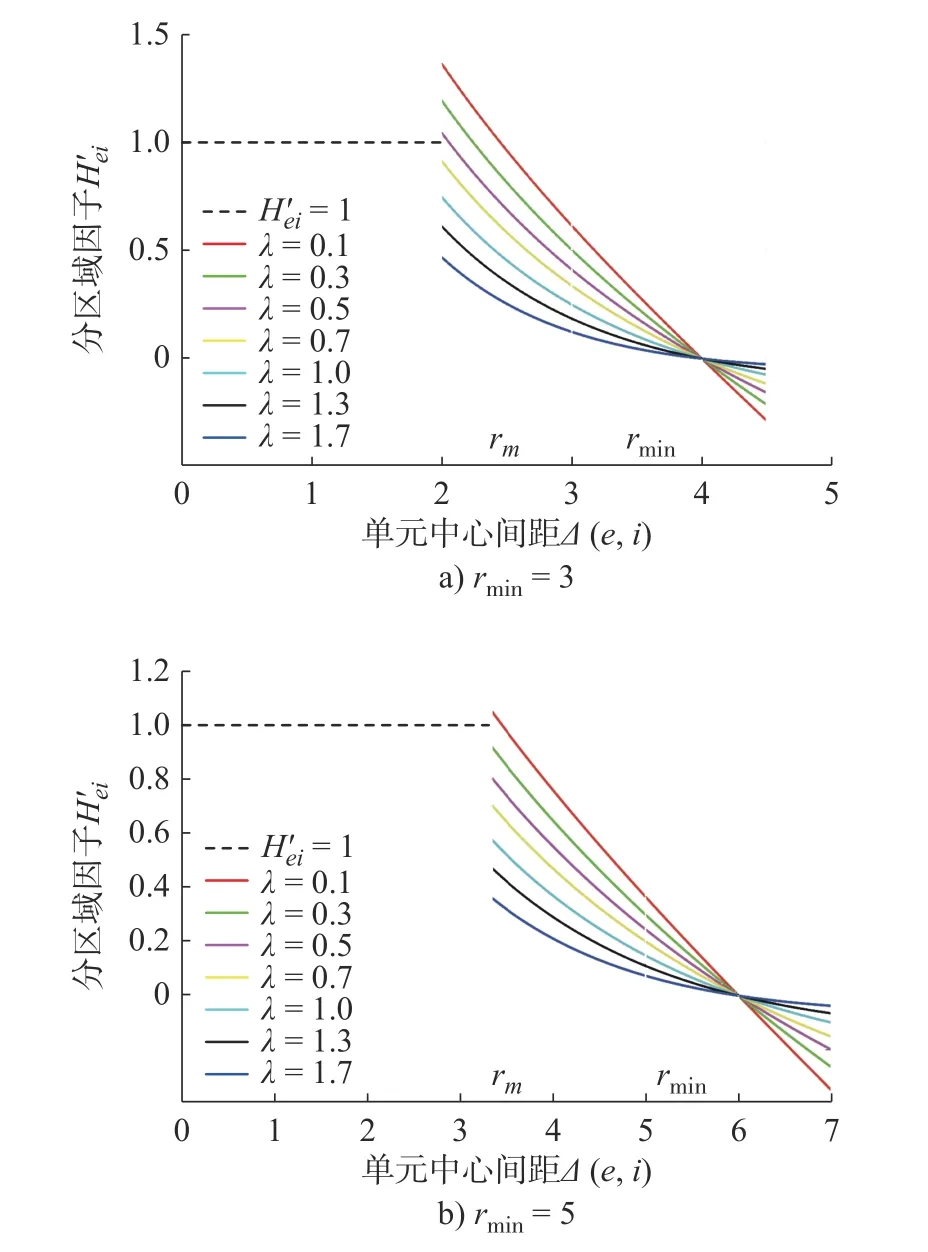
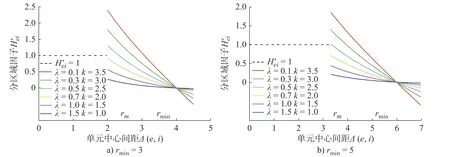
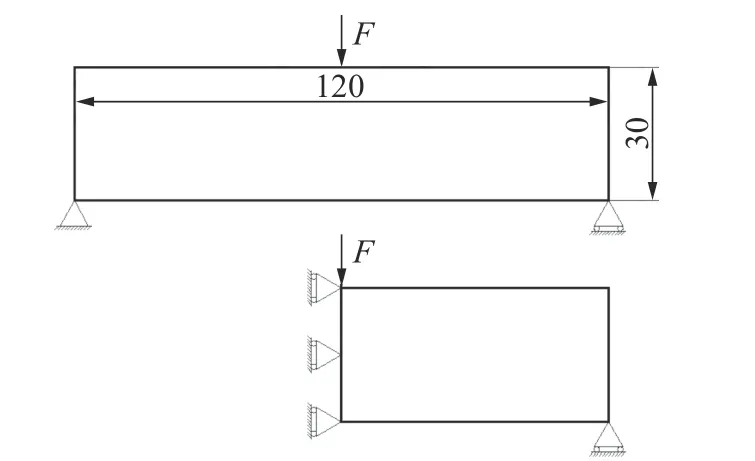
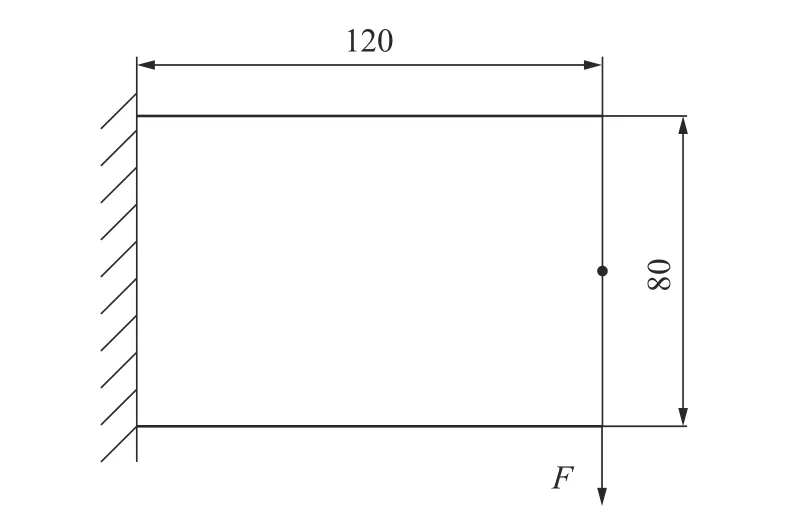
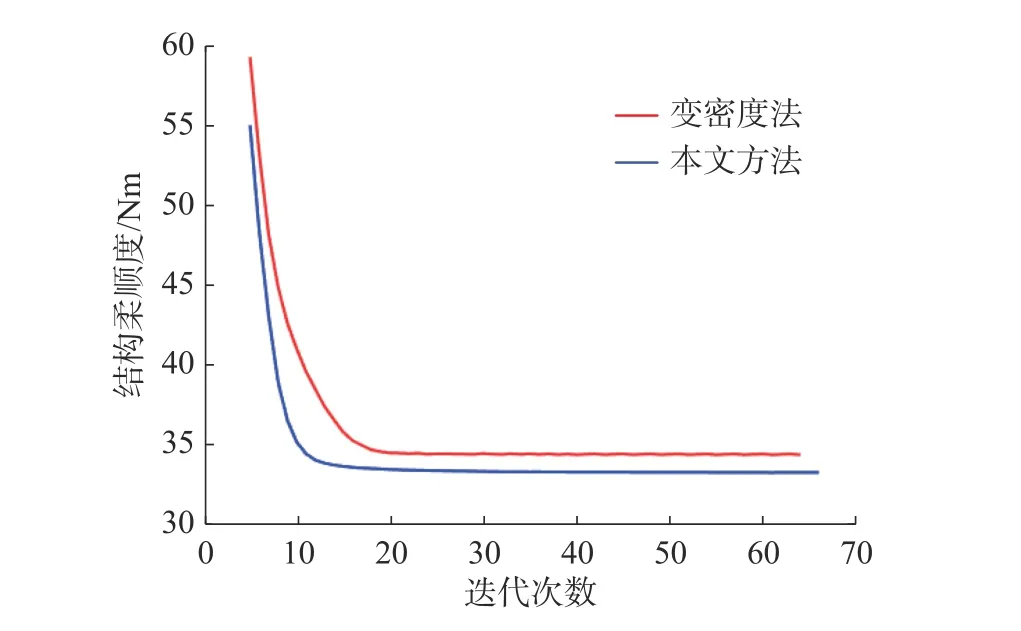
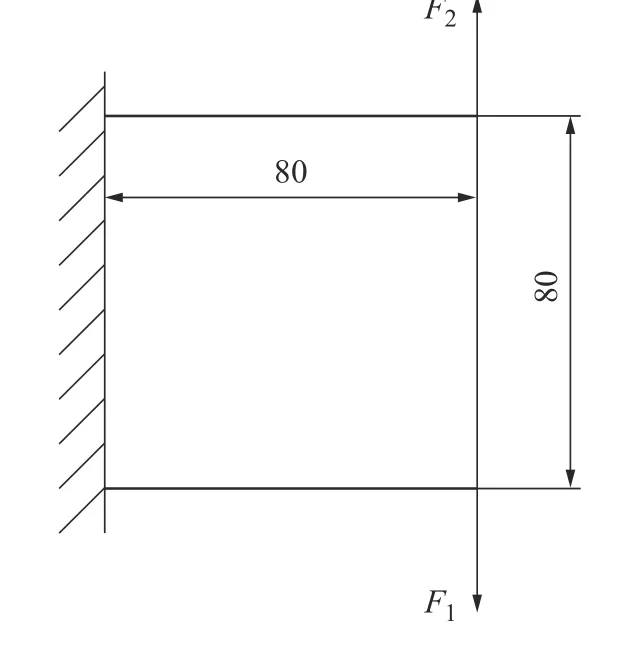
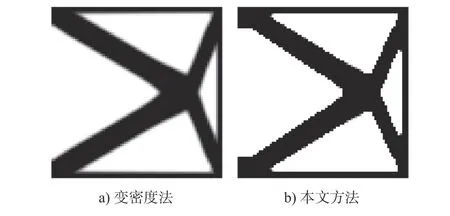
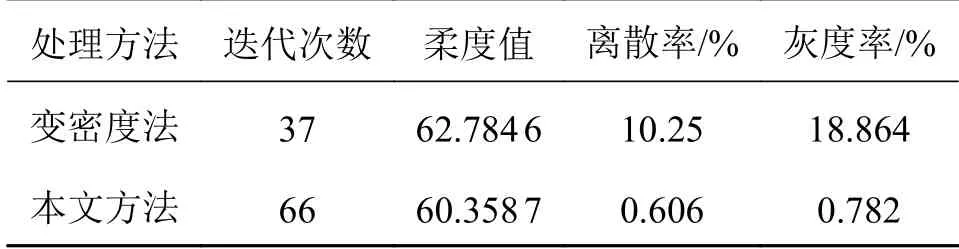
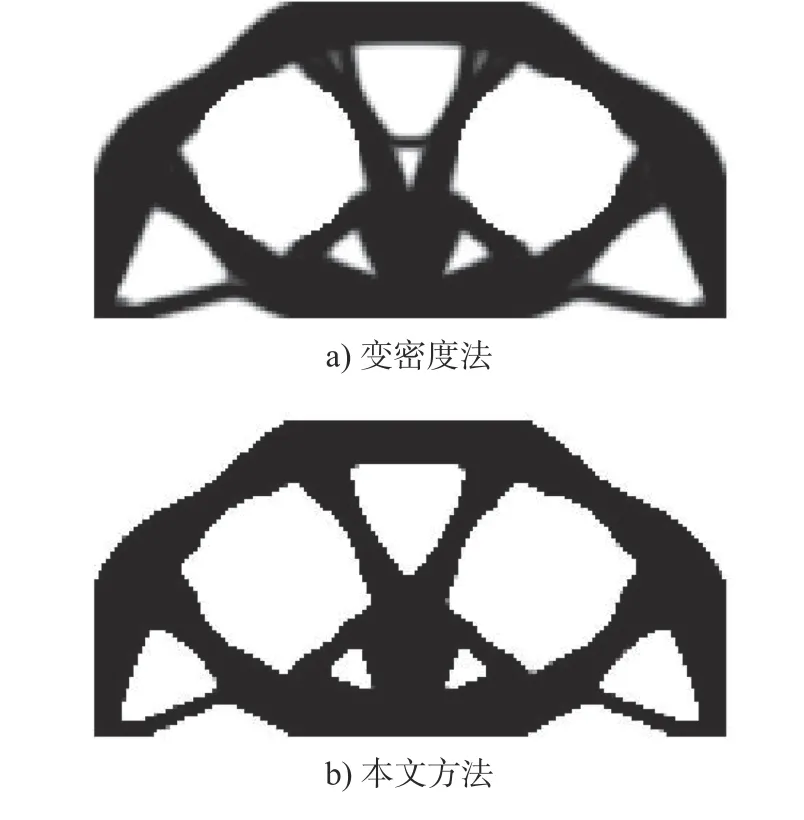
式中: ρi为单元i 的设计变量;p 为材料的惩罚因子,使设计变量 ρi趋近于0 或1; E(ρi)为第i 个单元的弹性模量; Emin为 孔洞元素的弹性模量; E0为实体元素的弹性模量;K 为插值处理后的刚度矩阵; ki为单元i 的刚度矩阵; ΔE=E0-Emin,为保证数值计算的稳定性,通常 Emin=E0/1000 , 且0 建立材料相对密度与材料弹性模量的函数关系,如图2 所示。 图2 变密度法密度插值函数模型 在给定的体积约束条件下,选取最小柔度作为目标函数,基于变密度法优化问题可表述为: 式中:ρ 为设计变量;C(ρ)为给定拓扑的柔度;U 是单元节点位移矢量;F 是元素节点负载向量;K 是全局刚度矩阵;N 为元素个数;k0是单位杨氏模量的元素刚度矩阵;V(ρ)是优化后结构体积;V0是设计域的体积;f 是预先设定的体积分数;ρmin是一个包含最低允许相对密度的向量。 优化准则法[18](Optimality criteria,OC)在拓扑优化中得到了广泛的应用,对于单约束拓扑优化而言,它是一种相当简单且易于实现的算法。其设计变量迭代公式可表示为 式中:t 为平移限度, t =0.2;ω 为阻尼系数,ω=0.5。参数t 与ω 用来控制迭代稳定及快速收敛,Be=为中间变量;ξ 为拉格朗日乘子,一般由二分法确定其值。 OC 算法的主要实现方式是利用目标函数与约束条件建立拉格朗日方程,将约束条件与目标函数结合成为无约束问题。结合式(3)所列目标函数与式(4)所列迭代设计变量,则优化准则法可表示为 通过分析计算,可确定最终设计变量的优化迭代准则可表示为 式中 ς为当柔度取极值时全设计域中元素的应变能密度。 当两次连续的目标函数迭代差值的变化率小于预设收敛率时,优化迭代终止,可表示为 目前在变密度法拓扑优化中普遍存在着棋盘格、网格依赖性现象。敏度过滤能够有效解决数值不稳定的问题,结构的灵敏度分析在进行拓扑优化时尤为重要,对模型的收敛判断具有决定性的作用。结构敏度可表示为 Sigmund 敏度过滤方法是一种局部约束方法,其本质是通过人为设定一过滤半径 rmin如图3 所示,在此范围内通过引入线性卷积因子将中心单元(红色)与其余单元之间(蓝色)的距离进行加权平均计算,进而修正目标函数的灵敏度,构建这一范围内所有元素的敏度均值,更新敏度后续的迭代处理,从而解决棋盘格问题。 图3 Sigmund 敏度过滤示意图 Sigmund 敏度过滤方法可表示为 式中: Hei为 卷积因子; rmin为 最小过滤半径; Δ (e,i)为元素i 到目标单元的中心距离,由于设计变量的取值为[0,1],取ρmin=10-3,防止造成计算上的奇异性。 由式(9)可看出,在敏度区域范围内,任一单元到中心单元的距离越远,其受到权重约束的程度越小,因对两单元距离进行加权平均计算处理,使得拓扑优化边界产生过度磨平的情况,形成灰度单元带,出现边界扩散问题。如图4 所示,当所设定的的过滤半径较大,边界含有过多低密度单元时,这种情况尤为明显。 图4 r min=5 时拓扑优化结果 本文提出分区密度修正的敏度过滤方法来克服Sigmund 敏度过滤方法中边界扩散的问题。其基本思想是将原敏度过滤区域划分为新的子区域,对不同的区域采用不同的敏度过滤因子,保证在提高中心位置近距离单元快速收敛迭代的同时,降低外围区域边界处单元的权重值,进而降低远距离单元对中心单元敏度的影响程度。同时采用一种带有预设修正权值的方法,进一步弱化边界扩散的问题。 如图5 所示,将原过滤半径为的区域进行划分为Ⅰ、Ⅱ两个子区域。其中Ⅰ区域的半径为rm,采用常数1 作为敏度过滤因子,即采用原Sigmund 敏度过滤因子,保证单元中心在Ⅰ区域中心单元(红色)的近距离单元(黄色)具有较快的收敛迭代速度。对单元中心在Ⅱ区域的远距离单元(蓝色)采用非线性函数因子处理,可以有效扩展卷积的拟合区域,以此降低该区域外围边界处单元的权重值,确保中心单元的敏度在迭代过程中不被过多的平均化,保证最终拓扑优化结果尽可能避免过度磨平的情况出现。 图5 敏度过滤区域划分示意图 分区域因子可表示为 采用一种带有预设密度修正权值的方法,自动判断单元敏度绝对差值大小,当差值大于预设阈值时,采用密度修正权值,进一步弱化边界扩散的问题。可表示为 式中:q 为预设密度修正权值, q=10-3; |ρi-ρe|为两离散单元密度差值 i ∈Ne; η为预设阈值,经数值计算验证发现 η过大则导致迭代速度过慢, η过小则容易出现细小结构,取η =0.8为宜。 综上可得分区密度修正的敏度过滤方法可表示为 为考量拓扑优化结果的收敛程度,Sigmund[10]最先提出引入离散率作为评价指标,其反映了中间单元密度值向0、1 两端收敛的程度,可表示为 式中:当全部单元密度 ρi为0 或1 时, Md=0取得最小值,表示所有单元均已离散;当全部单元密度ρi=0.5时 , Md=100取得最大值,表示所有单元均收敛。 为考量拓扑优化结果中灰度单元占比程度,引入灰度率作为评价指标,可表示为 式中: ρj表示密度值介于0、1 之间的灰度单元; v0表示预设的体积分数。 由图5 可知,半径rm的大小直接影响Ⅰ区域所含单元的个数,进而影响敏度过滤的效果。rm值过大时,因Ⅰ区域包含过多单元,并未有效弱化单元距离加权平均的效果,其趋向于文献[10]所得结果;rm值过小时,因Ⅰ区域包含较少单元,迭代过程中极易出现出现数值不稳定问题。由式(10)知rm取值与过滤半径rmin具有一定关系,因此,为研究二者关系并确定影响因子β 的值,对算例1 所示的二维应力结构进行拓扑优化,取惩罚因子p=2,假定修正参数k=2、λ=0.5,得到rm与rmin在迭代次数、柔度值、离散率及灰度率的分析结果,如图6 所示。 图6 不同β 值多指标分析示意图 由图6 可知,当β=1 时,具有较好的迭代速率,但因离散率及灰度率过高,不宜采用;当β=5 时,在4 个指标中均有良好表现,但优化结果容易出现数值不稳定的问题,不宜采用。综合多种因素考虑,取β 的值为3 附近时,具有良好的算法合理性及优化结果。 当β=3 时rm=rmin-,分别取rmin=3 与rmin=5,探究分区域因子 He′i的 修正参数k 与λ 随 Δ(e,i)的变化规律。假定k 一定,λ的变化曲线如图7 所示;假定λ 一定,k 的变化曲线如图8 所示;k 与λ 均变化的曲线如图9 所示。 图7 分区域因子修正参数k 一定λ 变化曲线 图8 分区域因子修正参数λ 一定k 变化曲线 如图7 变化曲线可知,当k、 Δ(e,i)一定时,λ 越小, He′i的值越大,曲线越陡峭;如图8 变化曲线可知,当λ、 Δ (e,i)一 定时,k 越越小, He′i的值越小,曲线越平缓。修正参数k 与λ 过大或过小均不利于获取较优的拓扑优化结果。如图9 变化曲线及式(10)可知,针对不同过滤半径rmin下,当 Δ(e,i)=1+rmin时He′i=0, 不同的修正参数得到的曲线所得到的 He′i的值在 Δ(e,i)=rmin处均大于0,有效避免了原过滤半径rmin在某种程度上缩小,保证在rmin范围内各单元均参与分析计算,使得原过滤半径rmin对优化结构的最小尺寸控制力,并保留了Sigmund 敏度过滤方法求解计算时的稳定性,确保了拓扑优化结果的可靠性,并采用一种带有预设密度权值的方法,进一步的弱化了边界扩散问题。 图9 分区域因子修正参数λ 与k 均变化曲线 为进一步研究修正参数k 与λ 对拓扑优化结果的影响,采用控制变量法仍对算例1 所示的结构进行拓扑优化来确定其值,取惩罚因子 p=3,过滤半径rmin=3, 影响因子 β=3,数值实验结果见表1 所示。 表1 不同参数计算结果 由表1 可知,不同参数组合所得结果的迭代次数、柔度值、离散率及灰度率有较大差异。综合考虑多种因素,设定参数 k=2 、 λ=0.5时,该方法具有较好的算法合理性和迭代效率。参数设定并不唯一,可根据具体研究对象略加调整。 采用多个拓扑优化典型算例来验证分区密度修正的敏度过滤方法(以下简称本文方法)在不同条件下的有效性及可行性,算例通过MTLAB-2016a 编程实现。在本文算例运行计算中,采用平面四结点双线性正四边形单元离散结构,实体材料的弹性模量 E =1, 泊松比ν =1, 惩罚因子 p=3[19]。 算例1 如图10 二维平面应力结构,该结构设计区域为120 mm×30 mm,左下角节点处采用固定约束,右下角节点处采用铰链约束,在图示结构上部中间节点处受到载荷F=1 的竖直向下载荷作用。该模型属于对称结构,为减小计算量,故采用模型一半结构进行分析。网格计算密度取60×30,过滤半径取rmin=3。 图10 算例1 模型示意图 通过对比变密度法、文献[10, 14-16]方法及本文方法的拓扑优化结果,分析及验证本文方法是否具有可行性。采用体积比为0.5 的约束条件,得到多种处理方法下的拓扑优化结果如图11 所示,不同指标对比结果如表2 所示。 表2 算例1 不同处理方法拓扑优化结果 图11 算例1 不同优化方法结果对比 对比上述实验结果可看出,除变密度法外,文献[10,14-16]方法及本文方法均能够获得边界清晰的拓扑优化结构,有效抑制边界扩散现象。然而,文献[10]方法迭代速率较为缓慢,文献[14]方法优化结果边界仍然存在个别数值不稳定现象,文献[15]方法不能保证其结构完整性,文献[16]方法优化结果仍存在部分灰度单元。对比上述方法,本文方法在有效获得清晰拓扑结构的同时,具有较快的收敛速度和较低的柔度值,对网格离散的控制较好,能有效控制结构,确保其完整性。 算例2 如图12 所示二维平面应力结构,该结构设计区域为120 mm×80 mm,结构左端采用全平面固定约束,结构右端中间节点处受到载荷F=1 的竖直向下载荷作用。 图12 算例2 模型示意图 通过选用不同参数,分析及验证本文方法在不同网格计算密度、不同体积比时是否具有可行性,采用体积比为0.5 的约束条件。拓扑优化结果如图13 所示,不同指标对比结果如表3 所示。 图13 算例2 拓扑优化优化结果 表3 算例2 优化结果 由上述实验b、c、d 在不同过滤半径条件下的优化结果对比可知,本文方法在不同指标下均具有良好的结果,在过滤半径较大时,有效抑制边界扩散问题。由实验b、e、f 在不同网格单元划分条件下的优化结果可知,本文方法在网格划分数目较多时,仍具有良好的结构性能。 为进一步验证本文方法是否具有稳定性,通过对比变密度法与本文方法,将实验a 与b 的柔度值进行数据处理。为清晰显示比较结果,从第五次迭代开始记录数据,结果如图14 所示。 图14 算例2 不同方法迭代曲线示意图 由图14 可知,本文方法较之变密度法具有更快的收敛速度,同时在结构柔度方面具有良好的稳定性。 算例3 如图15 所示二维平面应力结构,该结构设计区域为80 mm×80 mm,网格划分为80×80,结构左端采用全平面固定约束,在图示结构右上角受到载荷F=1 的竖直向上载荷作用,右下角受到载荷F=1 的竖直向下载荷作用。 图15 算例3 模型示意图 通过对比变密度法与本文方法拓扑优化结果,进一步分析及验证本文方法在多重载荷情况下是否具有可行性,采用体积比为0.4 的约束条件,过滤半径取rmin= 2。拓扑优化结果如图16 所示,不同指标对比结果如表4 所示。 图16 算例3 拓扑优化优化结果 表4 算例3 优化结果 由上述实验结果可知,本文方法在多重载荷情况下同样具有良好的可行性。其拓扑优化迭代次数稳定,优化结构的柔度收敛值较小,能有效控制离散率及灰度率指标。 算例4 图17 所示为二维平面应力结构,该结构设计区域为160 mm×80 mm,设计区域中两孔洞圆直径均为40 mm,左孔洞圆中心距左端面为45 mm,距底面为40 mm,右孔洞圆中心距右端面为45 mm,距底面为40 mm,网格划分为160×80。结构左下角节点处采用固定约束,右下角节点处采用铰链约束,在图示结构顶部中间节点处受到载荷F = 1 的竖直向下载荷作用。 图17 算例4 模型示意图 通过对比变密度法与本文方法拓扑优化结果,进一步分析及验证本文方法在含有多个孔洞结构的情况下是否具有可行性,采用体积比为0.5 的约束条件,过滤半径取rmin= 2。拓扑优化结果如图18所示,不同指标对比结果如表5 所示。 图18 算例4 拓扑优化优化结果 表5 算例4 优化结果 由上述实验结果可知,本文方法在含有多个孔洞结构的情况下同样具有良好的可行性。其拓扑优化迭代次数稳定,优化结构的柔度收敛值较小,能有效控制离散率及灰度率指标。对比图18 优化结果,较之变密度法,本文方法在一定程度上能够有效解决网格依赖性的问题。 变密度法在拓扑优化过程中常出现棋盘格现象等数值不稳定问题,使优化结果常具有灰度单元,致使优化模型提取较为困难。虽然Sigmund 敏度过滤方法能够有效减少数值不稳定问题,但该方法容易导致边界扩散,不具备良好的可制造性。为解决这一问题,本文在现有研究的基础上提出了一种分区密度修正的敏度过滤方法。实验结果表明,该方法能有效避免边界扩散等问题,迭代速度稳定,离散率及灰度率指标较低,同时能够降低柔度收敛值,提升结构刚度,保证结构完整性。当前,该方法仅适用于二维平面结构的拓扑优化,在今后的研究中,需进一步探究其在三维空间结构中的应用途径,进一步提升方法的适用性及有效性。
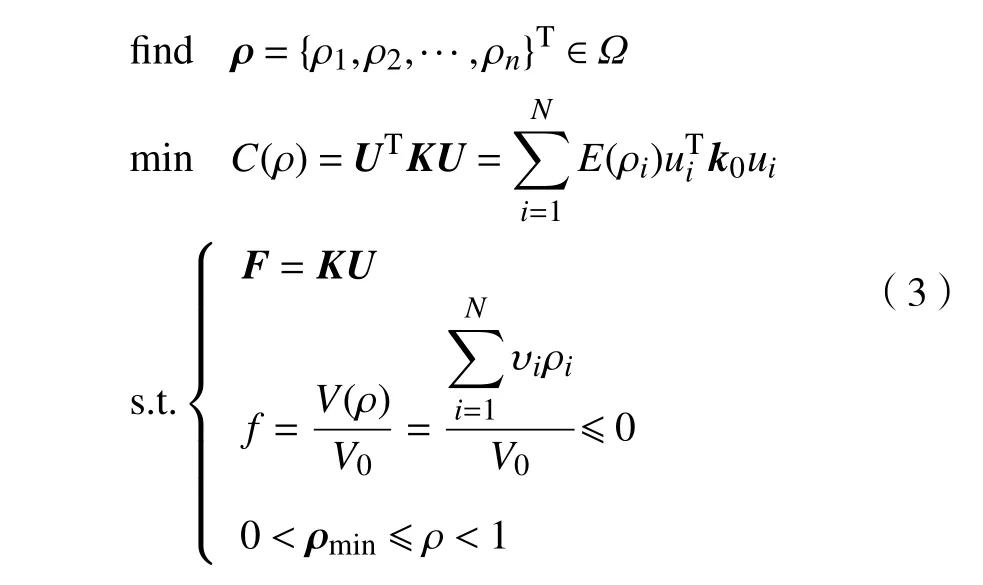
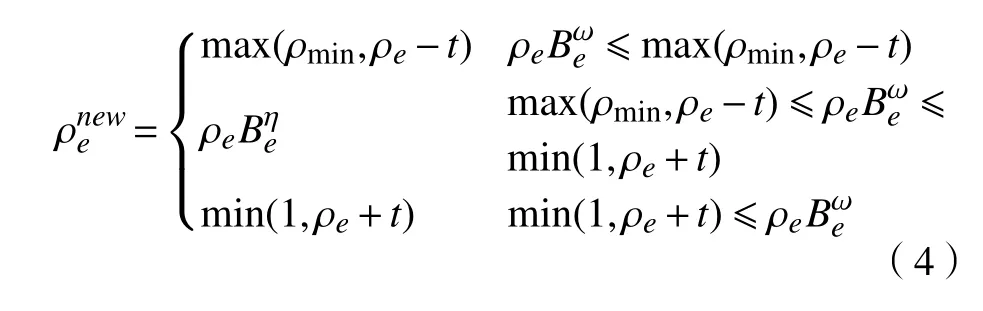

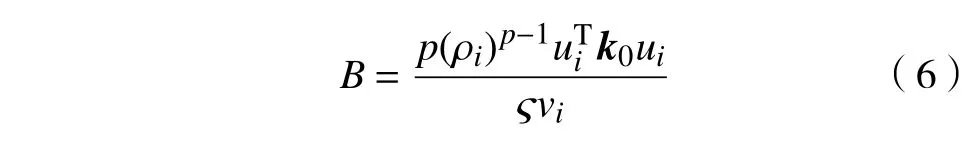
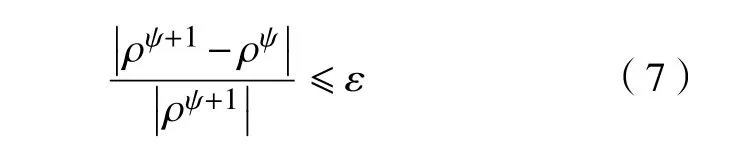
2 分区密度修正的敏度过滤方法
2.1 Sigmund 敏度过滤方法

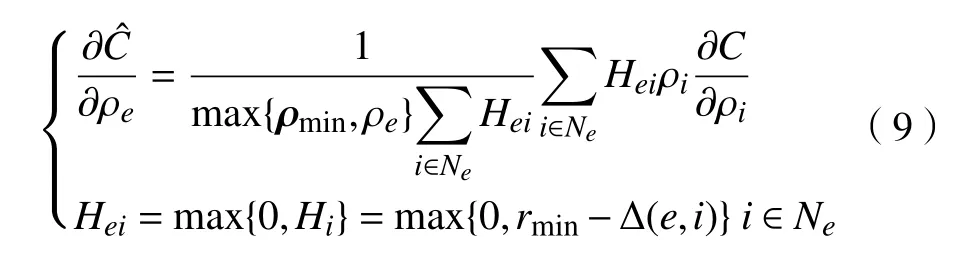

2.2 分区密度修正的敏度过滤方法

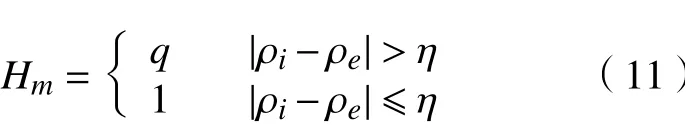
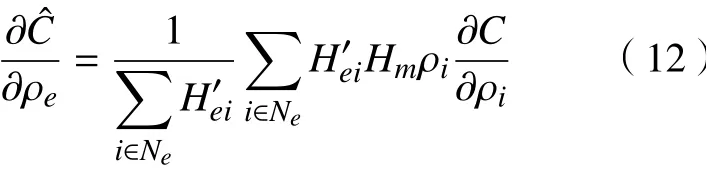


2.3 方法参数确定


3 实验验证






4 结论
