数控系统连续微线段加工方法研究

潘盛湖，胡涵，刘云强，张小军，冯一夫

（西南石油大学机电工程学院，成都 610500）

曲线高速、高精度加工是目前数控机床所面临的重大课题。发达国家如美国、日本等，由于研究起步较早，在曲线高速、高精度加工领域形成了垄断。近些年，国内在该领域加大了研究力度，取得了一些重要的研究成果。例如，焦青松等[1]提出基于离散曲率计算的连续小线段高速插补加工方法，并对前瞻技术进行了论述。许晨伟等[2]基于圆锥截线的有理Bézier 拐角过渡方法，实现不同类型圆锥截线与相邻小微线段的轨迹和速度的平滑过渡。高体红等[3]以圆弧过渡算法为基础，搭建了半硬件仿真测试系统验证了其有效性。沈斌等[4]将离散的微段数据点拟合成一条NURBS曲线并将其作为新的加工路径，然后利用NURBS曲线实时插补。李建刚等[5]将NURBS曲线进行区域分割，实现了小线段轨迹相对光顺。冷洪滨等[6]对采用三次样条曲线拟合方法对离散数据进行重构，从而进行样条插补以提高加工速度。司慧晓等[7]提出了基于圆弧的改进S型加减速算法，较常用S型加减速算法在整体上提高了一次幂从而提高了加工精度。李浩等[8]采用S型加减速方式实时地计算进给速度，实现了实时最优速度规划。游达章等[9]提出了单段的前瞻后顾算法，避免了单次连续速度规划对加工效率和平稳性的影响。

上述方法主要分为两种类型：一是不改变原轨迹，仅仅通过计算并限制拐角速度来进行直接过渡加工。该方法计算量小，但拐角点处所允许的加工速度较低，对整体加工效率提升有限；二是牺牲轮廓精度，在拐点处添加过渡曲线，增加曲线平滑度，提高拐角速度。该方法能有效提升加工效率，但会使轮廓精度降低，且加工数据计算量大大增加。

综上所述，本文提出了一种简单的、易于实现的基于曲线分段的连续微线段加工方法。该方法在满足曲线加工平稳的前提下，通过对曲线进行分段规划，实现曲线单元内速度均匀，曲线单元间加减速连续，既提高了曲线加工速度，又克服了频繁加减速对轮廓精度造成影响。

1 曲线分段加工思想

曲线加工是将理论上坐标点无穷的连续曲线通过一定的数学处理转化成数量有限、长度很短的微线段，在微小曲线加工方法上基本上采用微小直线插补逼近理论曲线[10]。与传统每一微小线段均需要按照“加速-匀速-减速”方式进行加工不同，本文采用的加工思想为：基于曲线分段插补原理，将曲线按照一定数学规律进行分段，即将一段或多段微线段组成一加工单元，如图1中曲线Pi-2Pi-1、Pi-1Pi等。每一加工单元内通过限制小线段转接处的最大允许速度进行直接过渡，单元间通过插入过渡圆弧来增加曲线分段点处的加工平滑度，兼顾高效与平稳，并保证了实时性。

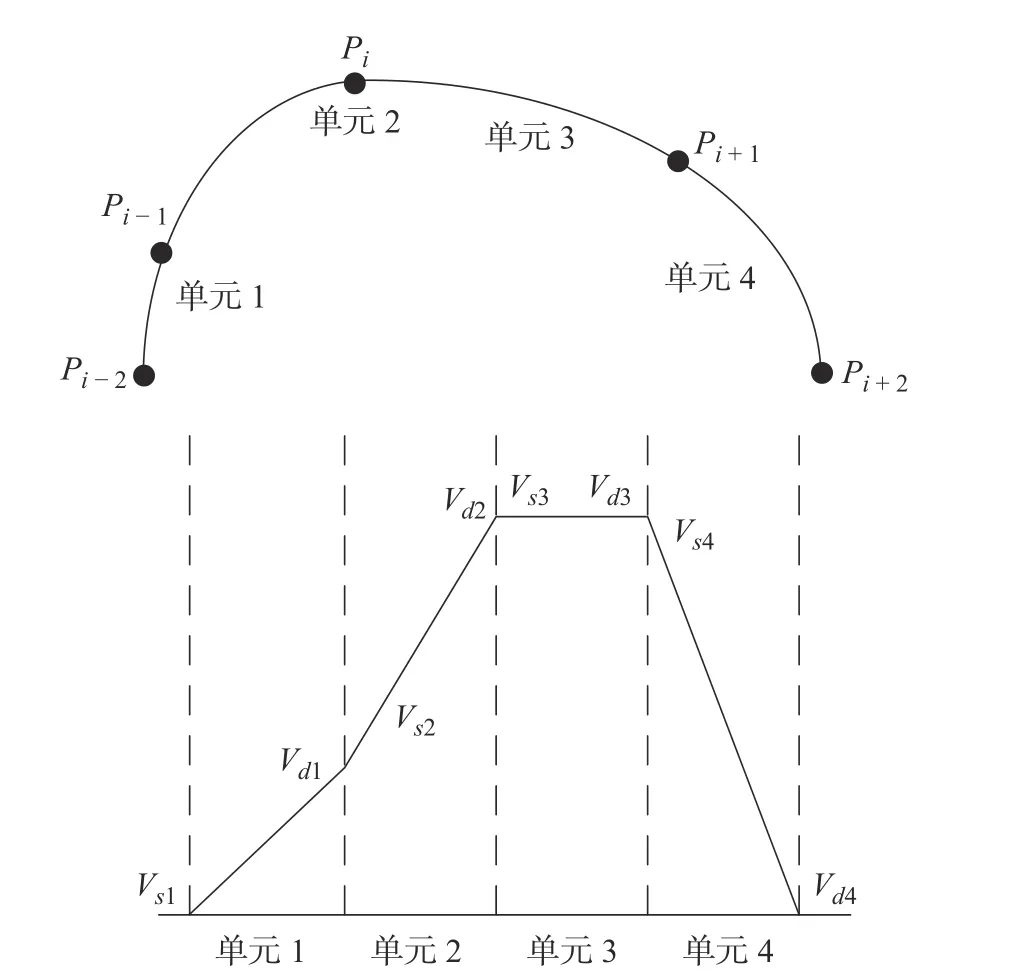
图1 曲线分段加工

2 分段加工方法模型

2.1 曲线分段识别算法

设Pi-1(xi-1,yi-1）,Pi(xi,yi）,Pi+1(xi+1,yi+1）为 曲线上微线段的连续3点并将其作为一个处理单元，可以近似地将曲线Pi-1PiPi+1看作圆弧段；其次利用用如图2所示的“离散三点法”求解圆弧半径并作为曲线Pi-1PiPi+1的曲率半径，即点Pi处的曲率半径；再次，采用微线段恒角速度加工原则，找出曲线加工允许的最大角速度为 ω，计算Pi点理论最大线速度Vi，并计算相邻两点线速度差 Δvi，最后以数控机床伺服系统允许速度跳动量为依据对曲线进行分段。

图2 离散三点法

分别求出点Pi-1Pi、PiPi+1、Pi-1Pi+1之间的线段长度Li-1、Li及 L′i，即：

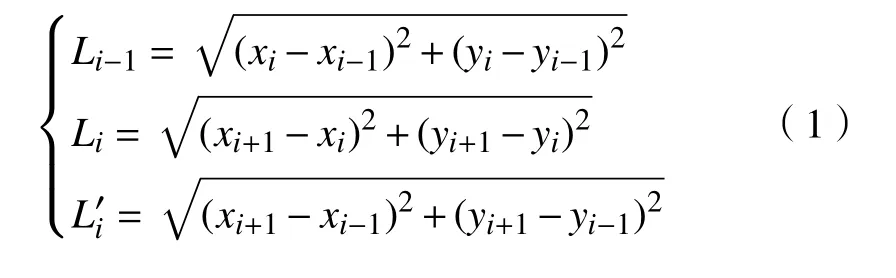
通过余弦定理及正弦定理可求得点Pi处的曲率半径[11]，基于微线段恒角速度加工原则，设曲线加工允许最大角速度为 ω，则点Pi处转角限制速度vm,i为

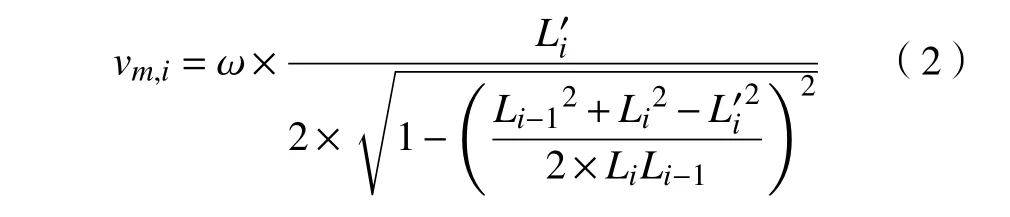
计算出相邻两个转角速度变化矢量的模为

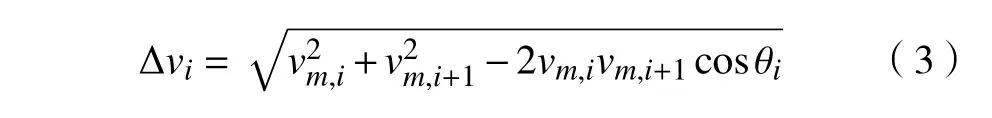
设机床允许的最大加速度为amax，插补周期为T，则允许的速度跳动量 Δvmax=amax×T。根据以下条件标识分段转角点：

1）当 Δ vi＜ Δvmax时，则转角点Pi为连续转角点，否则，点Pi为分段转角点；

2）当加工图形中有多条曲线时，每条曲线终点直接设置为分段转角点；

3）根据控制系统内存空间等情况，限制每次处理的微线段数N，每次处理中第N 段微线段转角点为分段转角点。

通以上步骤，得出分段算法流程如图3所示。

2.2 段间平滑过渡模型

如图4所示，Pi-1Pi、PiPi+1分别是相邻两曲线段的最末及最初小线段，Pi为分段拐角点。在两线段中插入过渡圆弧Q0Q1Q2，其中Q1为圆弧的中点，Q0和Q2分别是圆弧Q0Q1Q2与Pi-1Pi及PiPi+1的切点，同时也是过渡圆弧的接入点和转出点，为了便于分析，以Q0为坐标原点建立直角坐标系[12]。

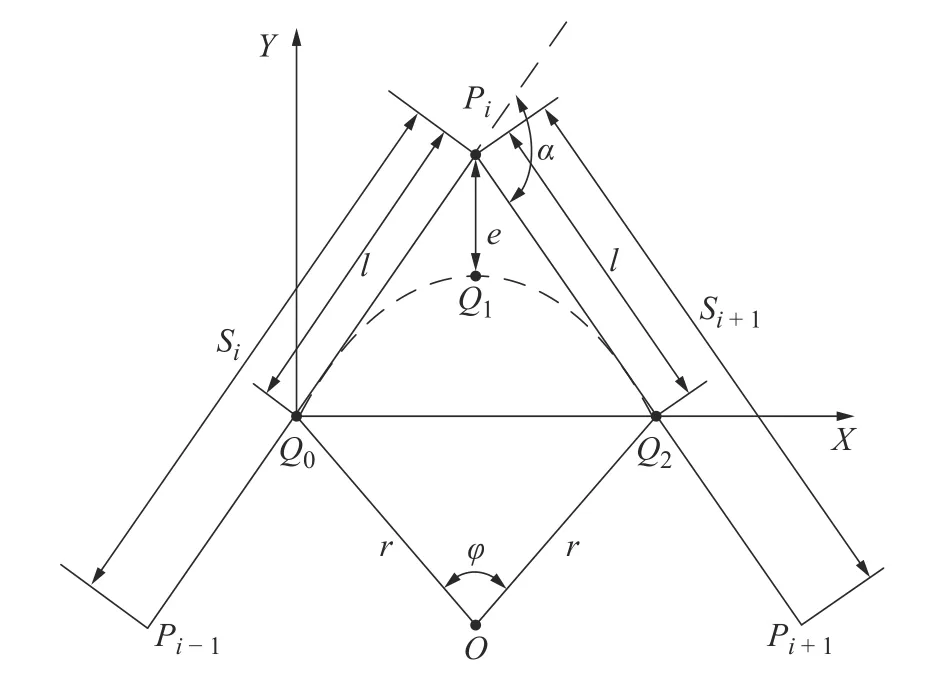
图4 段间平滑过渡模型

根据几何关系，可求得圆弧过渡所需过渡距离l 与过渡圆弧半径r 为：

在加工路径中插入过渡圆弧后，实际的加工路径会产生一定的轮廓误差，为满足精度要求，需通过最大轮廓误差来Em来限制过渡距离和过度圆弧半径，将Em代入式（5）可得由最大轮廓误差限制的过渡距离lc与和过渡圆弧半径rc为

从而计算出过渡圆弧段的最大进给速度vm,i为

2.3 分段加工速度规划算法

得到了连续微小线段间及圆弧分段拐角点的速度限制公式后，在对加工曲线进行分段处理成各曲线段单元后，利用式（2）求出单元内各转角点限制速度，并利用式（6）求出单元间过渡圆弧段最大进给速度，从而所有微小线段间的转角限制速度vm,i均求得。

基于对称加减速原则，设第i 段小线段的长度为Si，加工加减速度为ai。将从起点到终点视为一个连续的加速过程，终点到起点视为一个连续的反加速过程，分别计算每个转角点通过加减速能达到的速度[13-15]。

在正向加速规划阶段，取第i 段小线段入口速度vs0,i，经过距离Si的正向加速后，求得出口速度前一段的出口速度与后一段的入口速度相等，即vs0,i=vst,i-1。默认首段入口速度vs0,0=0，迭代计算出每一小线段的入口速度vs0,i和出口速度vst,i。

同理，在反向加速规划阶段，取第i 段小线段出口速度vdt,i，经过距离Si的反向加速后，求得入口速度后一段的入口速度与前一段的出口速度相等，即vdt,i-1=vd0,i。默认末段出口速度vdt,N=0，迭代计算出每一小线段的入口速度vd0,i和出口速度vdt,i。

以第i-1段和第i 段小线段衔接为例进行实际加工速度规划。如图5所示，若该衔接段为曲线分段单元内衔接，则点A处速度vm,i为转角限制速度，否则为过渡圆弧段的最大进给速度。点B 处速度为通过正向加速规划所得第i 段的最大入口速度vs0,i，点C 处速度为通过反向加速规划所得第i 段的最大入口速度vd0,i。为了保证加工的平稳性，实际的加工速度同时受到vm,i、vs0,i、vd0,i三者制约，最终的实际加工速度 vi=min{vm,ivs0,ivd0,i}，因此实际加工速度曲线图像会下移至虚线位置。

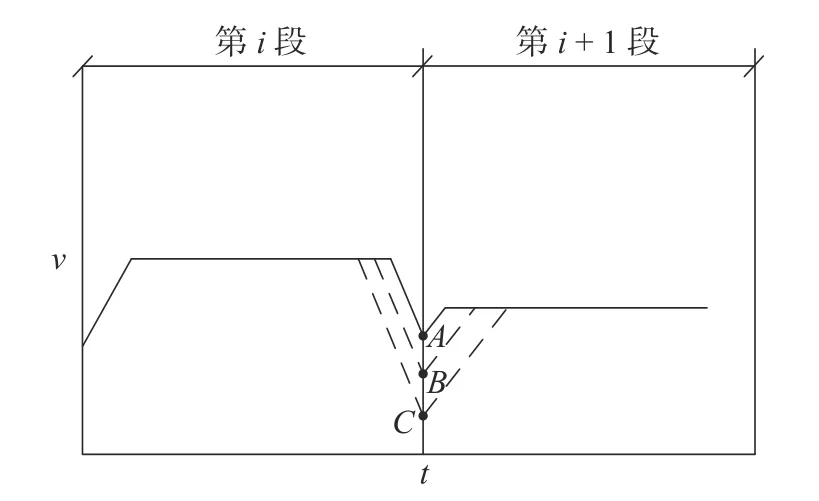
图5 速度规划原则

3 加工方法验证

本加工方法主要用于曲线加工机床，并在平面非金属切割机床上进行了曲线加工实验。机床最大加速度a=500000 pps/s2，最大进给速度f=80000 pps/s，坐标轴分辨率0.001 mm/pps，采用线性加减速方式，加工曲线为1094段微线段组成的封闭曲线，曲线如图6所示。

图6 加工数据曲线

利用本文算法完成对加工曲线的分段规划，将进行速度规划后的数据送入加工任务实现曲线连续加工。设置前瞻加工数据缓冲区RQ[N][K]，缓冲区长度变量LEN，循环变量SPRM，当前缓冲区可用数据段标志avail，数据结束标志END，设置曲线插补缓存RP[M]，实现曲线连续加工流程如图7所示。

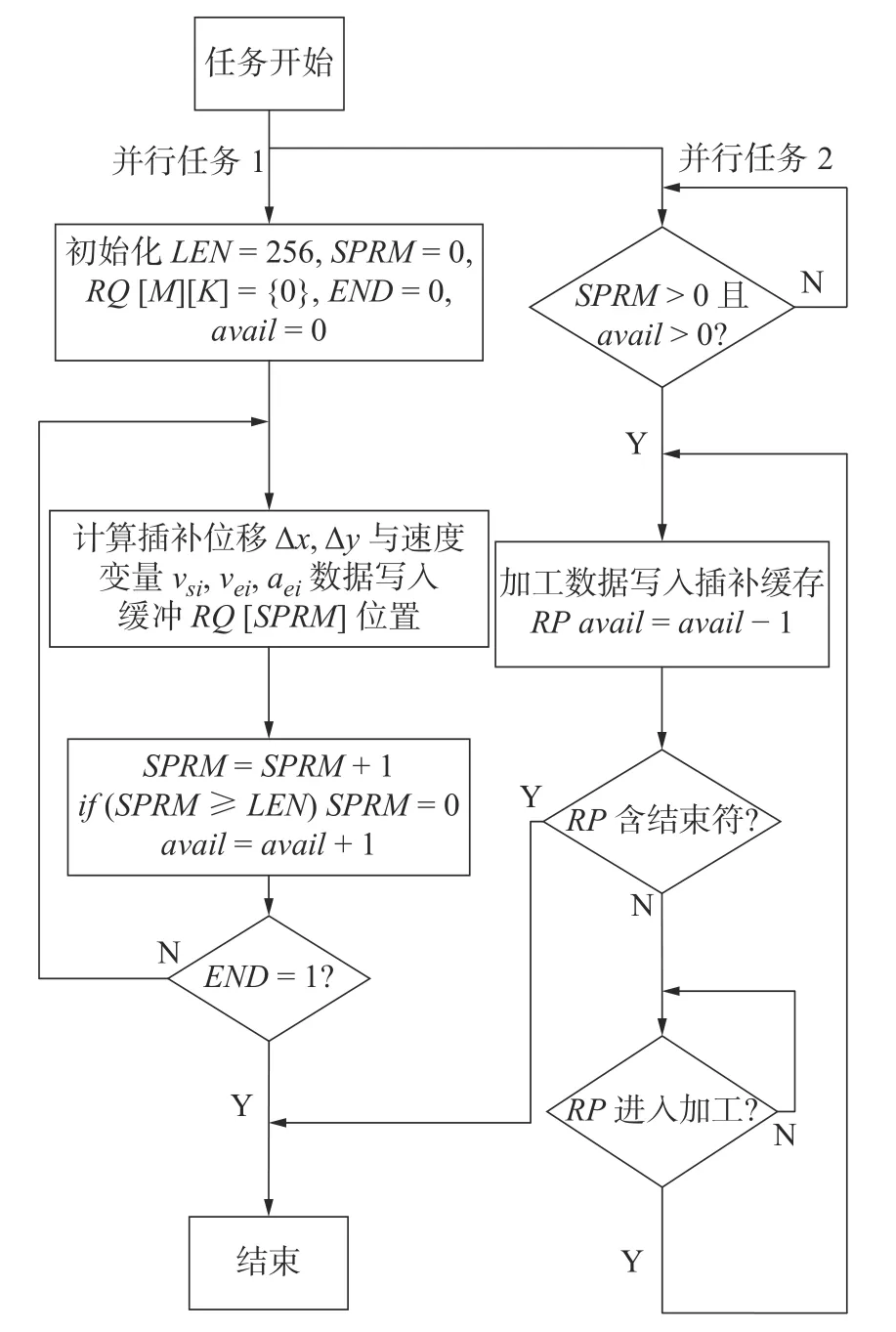
图7 曲线连续加工流程

加工实验平台如图8所示，上位机软件将加工曲线图案转化为加工数据传输给运动控制板后，由控制芯片内预先编写好的各加工方法程序进行路径及速度规划，最终驱动电机进行实际加工。

图8 加工实验平台

将本文加工方法、传统普通加工方法以及自适应前瞻加工方法分别进行加工实验，实时采集运动控制板输出到电机的脉冲信号频率作为加工速度数据，通过串口将数据传输至上位机，绘制时间与速度关系曲线图，得到如下实验结果并进行分析。

普通加工方式速度曲线如图9所示。每段微小线段都按照“加速-匀速-减速”方式运动，加减速频繁，速度不连续，严重影响加工质量。

图9 普通直线插补加工速度曲线

自适应加工方式速度曲线如图10所示。根据线段长度的约束求得当前线段最大前瞻速度，以最大前瞻速度计算其减速到0所需的距离并以此距离在后续线段中取出前瞻段数，得到速度前瞻规划区间，实现根据线段长度和加工轨迹的变化趋势来自适应地选取每次前瞻速度规划的段数，提高计算效率。该方法产生的速度曲线较为连续、光滑，但是曲线在加工过程中加减速仍然较多。

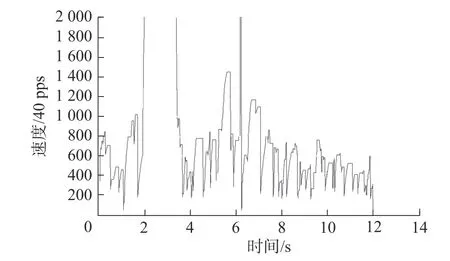
图10 自适应加工速度曲线

分段加工方式速度曲线如图11所示。每个曲线单元为一个加工主体，每一加工单元只执行一次“变速”过程，加减速次数比自适应加工方式少，且单元与单元之间采用速度优化衔接，曲线速度连续。

图11 分段加工速度曲线

在相同加工条件下，3种加工方法加工性能对比如表1所示，分析如下：

表1 加工性能对比结果

1）在加工时间上，分段加工方法用时最短，效率最高；

2）在加减速次数上，分段加工方法最少，普通加工是其它加工方法数倍；

3）在运动平稳性上，分段加工方法由于加减速过程最少，运动比其它加工方法平稳。

4 结束语

本文在对当前通过限制转角速度加工以及进行圆弧过渡加工两种方法研究的基础上，结合两种方法的优点，提出了一种简单、易于实现的曲线微小线段分段加工方法。在曲线单元内限制其转角速度，单元间进行圆弧过渡，实现了每个单元内速度变化均匀，单元间过渡平滑，提高了曲线加工过程运动的平稳性。经过实际加工分析，该加工方法达到了设计目的，符合微小线段高速连续加工的要求，具有一定的实际应用价值。