修形圆锥滚子轴承参数化建模方法研究
2022-12-02赵文哲刘创来黄立赵海涛孟凡明
赵文哲,刘创来,黄立,赵海涛,孟凡明*,
(1.重庆大学机械传动国家重点实验室,重庆 400044;2.中国船舶重工集团公司第七〇五研究所,西安 710077)
圆锥滚子轴承被广泛应用于铁路车辆、精密机床、汽车工业等领域的核心部件中,为了延长其使用寿命,工程应用中多对滚子或滚道修形来降低滚子两端的应力集中,进而提升其使用寿命[1]。目前常用的修形方式主要有圆弧修形、对数修形等[2]。滚子修形的概念被提出后,国内外学者通过数值分析的方法对修形滚子轴承的动、静力学性能进行了较多的研究[3-5],但该方法往往无法考虑轴承系统的全部自由度。为克服这一问题,近些年来部分学者开始借助一些成熟的商业软件对圆锥滚子轴承的动、静力学性能进行分析[6-8]。但在这个过程中轴承模型的创建和修改往往会耗费大量的时间与精力,为降低频繁创建、更改和导入模型的工作强度,国内一些研究人员参考现有其他机械结构的参数化建模技术[9-11],通过对某些商业软件进行二次开发,实现了在部分CAE 软件内部参数化创建或修改滚动轴承三维模型。例如郭艳朋等[12]、张磊等[13]通过对有限元软件APDL 进行二次开发,实现了圆柱滚子轴承、角接触球轴承及深沟球轴承的参数化建模。胡广存[14]、张军飞[15]也在ADAMS中实现了无修形的圆锥滚子轴承参数化建模,较大程度减轻了三维模型建立、修改时的难度和工作强度。
上述建模方法均无法实现轴承滚子修形结构的创建,并且未能精确考虑轴承各元件间的结构关系。本文提出了一种参数化建立考虑修形的圆锥滚子轴承模型的新方法,把结构较为复杂的修形圆锥滚子分为3部分,在不同的坐标系下分别建模,简化了修形滚子的数学模型,并对ADAMS进行二次开发,实现了修形圆锥滚子轴承的参数化建模。此外,将该方法与在Creo中建模的方法进行对比,验证了该建模方法的准确性和快速性。
1 圆锥滚子轴承基本结构
相对于其他类型的滚动轴承,圆锥滚子轴承的结构更为复杂,尺寸更多,各元件间的联系也更为紧密。以外圈大端面与轴承轴线的交点为原点o,轴承轴线为x 轴,垂直x 轴且指向外圈外表面的方向为z 轴,得到单列圆锥滚子轴承的结构示意如图1所示。其整体结构主要包括轴承外圈、内圈、滚动体以及保持架四部分,标准的圆锥滚子轴承应保证轴承外滚道延长线、内滚道延长线、滚子中心轴线以及轴承中心轴线四线交于一点A。
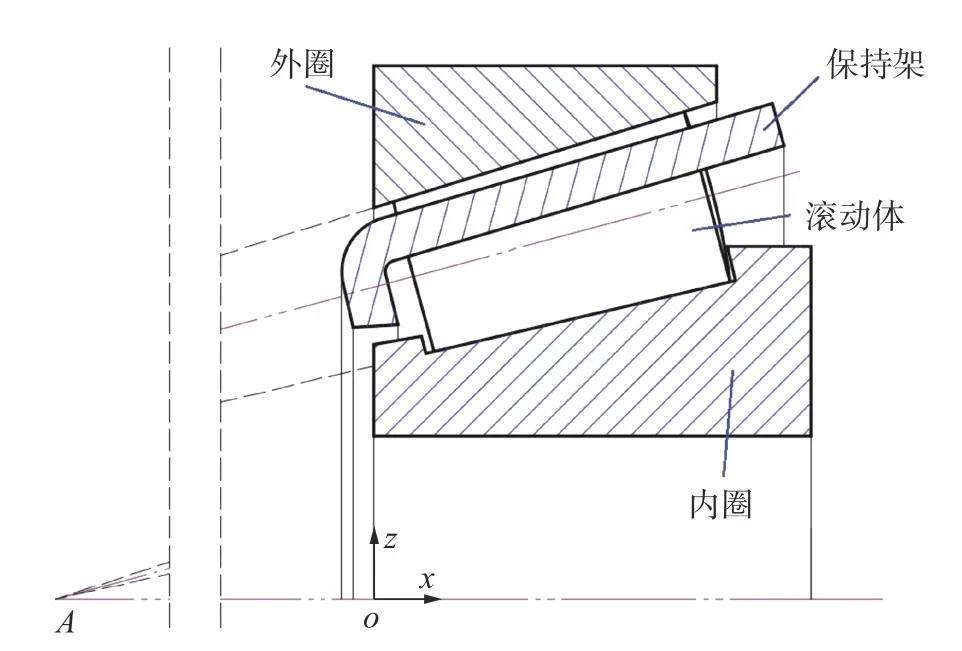
图1 圆锥滚子轴承整体结构图
2 圆锥滚子轴承数学模型
2.1 轴承内外圈数学模型
为提高参数化建模的效率,对圆锥滚子轴承内外圈模型进行了适当简化,略去内滚道与挡边之间的油沟,部分位置的倒角等。圆锥滚子轴承内外圈在xoz 平面内的结构示意如图2所示。
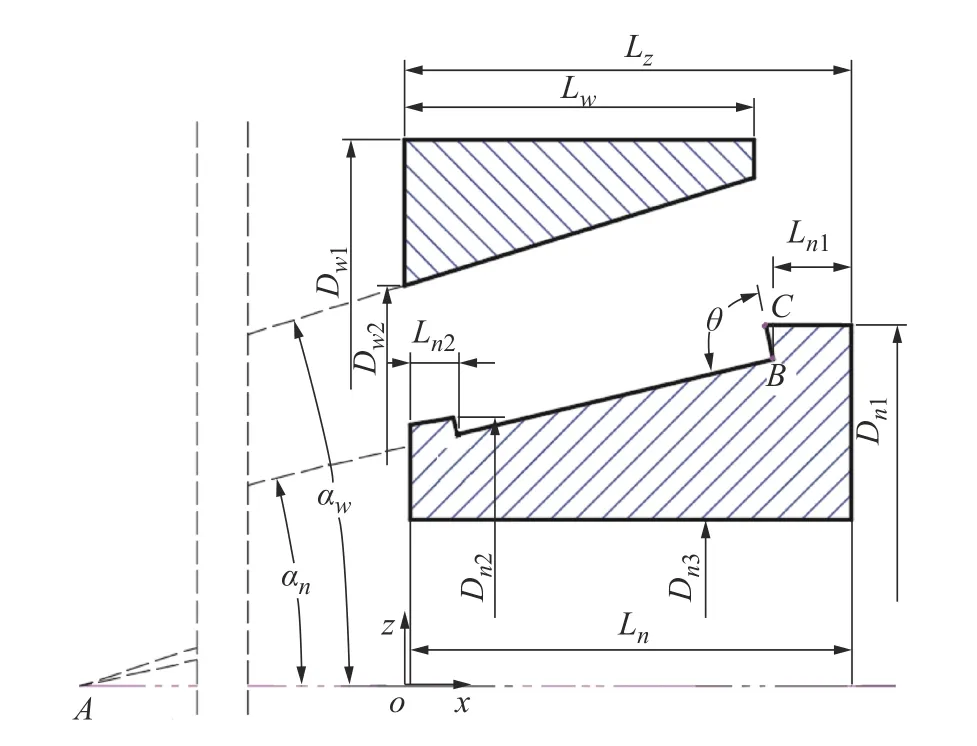
图2圆锥滚子轴承内外圈结构图
图2 中的参数均为轴承内外圈建模时的主参数,即建模时需要用户输入的参数,其物理意义如表1所示。

表1 圆锥滚子轴承内外圈主参数
根据表1中的主参数结合三角函数计算可得到圆锥滚子轴承内外圈各个顶点的坐标值,轴承内外圈的创建关键在于内滚道及大挡边的创建,记大挡边的两顶点坐标分别为为(Bx,By,Bz)、(Cx,Cy,Cz),由图2可知两点的y 坐标值均为0。首先得到轴承内外滚道与轴线的交点A距坐标原点o的距离LAo,结合三角函数关系可得

结合标准圆锥滚子轴承各元件间的结构关系和表1中的主参数值,可得B 点的坐标值为:
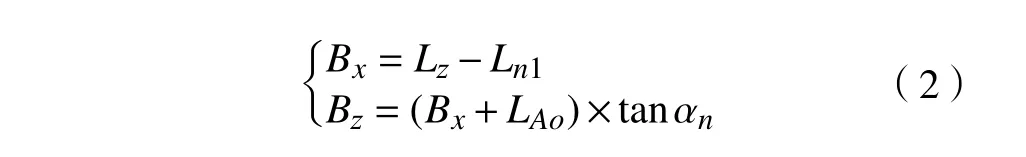
根据大挡边与内滚道间的夹角值和部分主参数值,可得C 点的坐标值为:
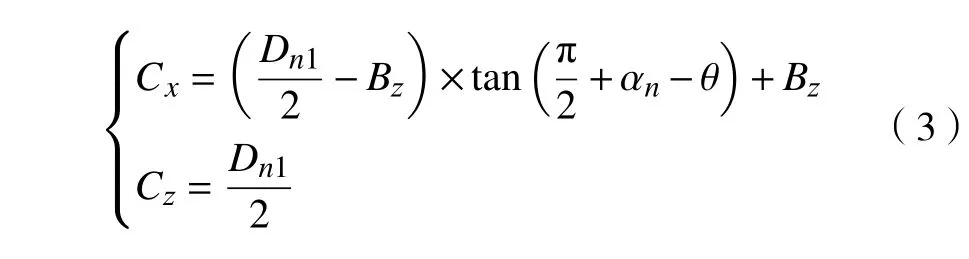
相似的方法也可以得到小挡边顶点的坐标值及轴承内外圈其他各关键点的坐标值。
2.2 修形圆锥滚子数学模型
为简化修形圆锥滚子的数学模型,将修形圆锥滚子分为修形部分、主体部分以及球端面3部分,并在滚动体小端中心和母线中点处分别建立局部坐标系o′x′z′和o″x″z″,在局部坐标系内构建修形滚子的数学模型,得到的修形圆锥滚子轴承滚子结构示意如图3所示。图3中O2点为滚子球端面的球心,细实线为滚子未修形时的轮廓,粗实线为修形过后的滚子轮廓,虚线为修形部分和主体部分的分割线。

图3 修形圆锥滚子轴承滚子结构示意图
本文研究的修形圆锥滚子均为两端修形量相等的全凸度修形,故修形母线在o″x″z″坐标系内关于z″对称。修形方式主要包括圆弧修形及对数修形,不同修形方式的修形母线方程可表示为:
1)圆弧修形
设圆弧修形半径为R1,其圆心在 z″轴上,则在o″x″z″坐标系下,圆弧修形母线方程可表示为
式中Ly为滚子的有效长度。
2)对数修形
文献[16]在对数修形方程中加入了两个修形参数,得到对数修形母线方程的通式,其在o″x″z″坐标系下表示为[16]
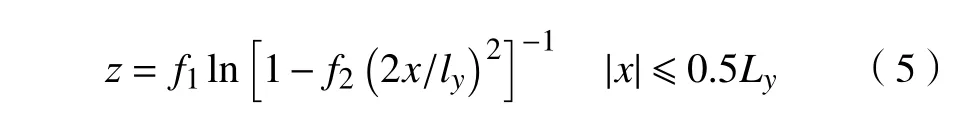
式中f1和f2为修形参数,f1单位为mm,f2无量纲。
由于该方程中仅有两个修形参数,在参数化建模时需要输入的参数较少,在实际工程应用中更为方便,故本文所选取该方程作为对数修形滚子的修形母线方程。除修形参数外,考虑修形的圆锥滚子在参数化建模时的主参数如表2所示。

表2 圆锥滚子轴承修形滚子参数mm
图3中除去主参数之外的参数为辅助参数,所有的辅助参数均可以使用主参数表示,不需要用户手动输入,这些辅助参数的物理意义如表3所示。

表3 圆锥滚子轴承修形滚子辅助参数
结合图3可求得表3中辅助参数的计算公式,其中修形滚子的最大修形量为:

式中:δ1、δ2分别代表修形方式为对数修形和圆弧修形时修形滚子的最大修形量。
修形后的滚子大径、小径的计算公式为:
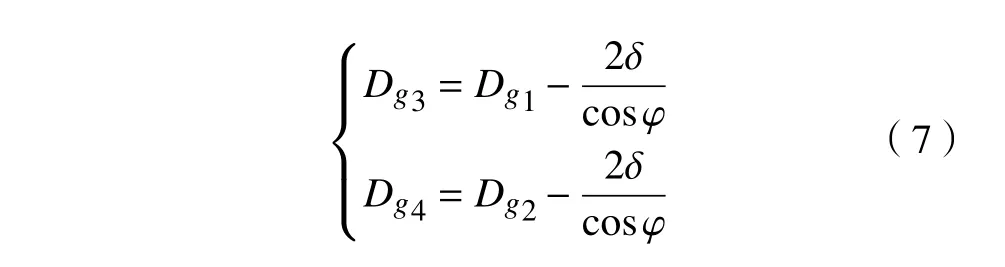
求出所有的辅助参数之后便可求得滚子球端面球心在o′x′z′坐标系内的坐标值。记O2点的坐标为(xO2,yO2,zO2),由图3可知 yO2和 zO2均为0, xO2的计算公式为
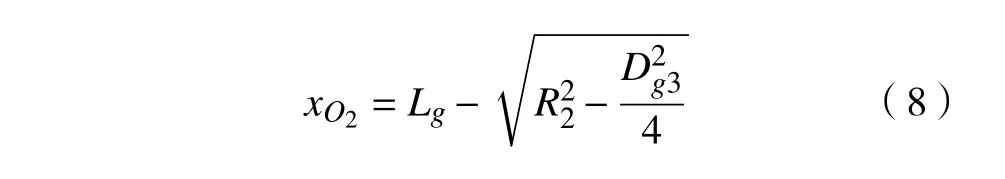
2.3 保持架数学模型
由于圆锥滚子轴承的保持架结构缺少统一规范,针对不同用途的圆锥滚子轴承,其保持架结构可能不尽相同,故本文选取较为常见的“7”字型保持架来参数化建立其模型,兜孔结构为圆弧兜孔。类似的,得到圆锥滚子轴承保持架结构示意如图4所示。

图4圆锥滚子轴承保持架结构示意图
图4 中:Ldk表示兜孔长度,RdE表示在E-E 截面上兜孔的半径,随着E-E 截面的变化,RdE的值也会不断变化,这两个参数是保持架建模时的辅助参数,不需用户手动输入。图4中其他参数为保持架的主参数,其物理意义如表4所示。

表4 圆锥滚子轴承保持架主参数
结合图3与图4中的参数可得到兜孔长度Ldk的表达式为
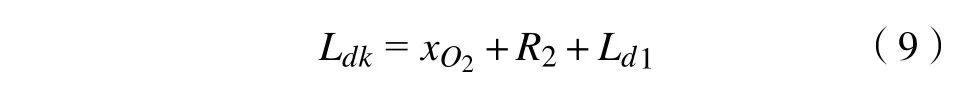
由于圆锥滚子轴承保持架的兜孔为一个圆台体,故记兜孔大径为Rd1,兜孔小径为Rd2,可得兜孔大径Rd1和兜孔小径Rd2的表达式为:

3 圆锥滚子轴承参数化建模
3.1 参数化建模流程
本文采用设计变量建模的方法实现参数化创建修形圆锥滚子轴承三维模型。该方法的优点在于除了可以快速创建模型之外,还可以通过修改设计变量的方式实现快速更改模型,而不需要重新建立模型,其具体的参数化建模流程如图5所示,图中的细节处理一项主要包括模型倒圆角、干涉检查等。

图5 圆锥滚子轴承参数化建模流程
3.2 参数化程序编写
修形圆锥滚子轴承参数化建模过程中主要用到的指令有“part create”、“revolution create”、“frustum create”等,轴承元件不同使用的指令也不尽相同,其使用到的主要指令及功能见表5。

表5 主要操作指令及功能
圆锥滚子轴承的参数化建模过程中,修形滚子创建是整个过程的重点和难点,用到的操作指令也最多,其中修形部分的创建最为重要,需要在指定坐标系下使用“Spline create”指令创建B样条曲线,再通过“Matrix create”指令创建修形方程的矩阵并赋值于B样条曲线,完成修形曲线的创建。之后通过“Revolution create”指令得到修形部分的三维模型,并通过“Boolean unite”与主体部分和球端面黏接为完整的修形滚子三维模型,最后生成的圆弧修形圆锥滚子三维模型如图6所示。
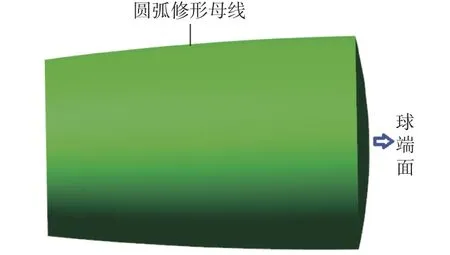
图6 圆弧修形滚子三维模型
单个修形滚子创建完成后通过“Object copy”指令实现对修形滚子的阵列操作。类似的,保持架兜孔也可通过类似的方法创建,再通过“Boolean intersection”指令依次与保持架主体部分进行布尔减操作得到轴承保持架的三维模型。最后通过编写的宏命令完成修形圆锥滚子轴承各元件的装配及细节处理,得到使用参数化方法创建的修形圆锥滚子轴承整体三维模型如图7所示。

图7 圆锥滚子轴承三维模型
4 实例分析
4.1 建模准确度对比
由于滚子修形最大的作用在于改善滚子母线方向上的应力分布,减弱或消除滚子两端的应力集中现象,故本文以圆锥滚子轴承滚子-内滚道间的接触应力分布为对象,对比分析参数化创建的模型和通过Creo软件创建的模型,并将模型导入ABAQUS中进行接触应力分析,最终通过计算两者应力分布曲线的平均相对误差值γ 来评判两者的差异度。其中平均相对误差γ 的计算方法为

式中:m为滚子母线上划分的节点个数,m=200;Pc,i为Creo中建立的模型在节点i 处的接触应力值;Pp,i为参数化建立的模型在节点i 处的接触应力值。对于接触应力等于0的区域,γ 的值为0。
以32310轴承为例,分别对比了不同修形方式、修形量以及不同载荷条件下两种模型的滚子-内滚道接触应力分布情况。其中最大修形量δ 分别取25.560μm、10.456μm、4.1245μm[16],分别对应大、中、小的修形量,载荷值分别取10 kN 和5 kN,分别对应轴承受重载和中载的工况条件。选取载荷为10 kN,最大修形量为10.456μm 时两类模型的接触应力分布进行对比,并将结果代入式(11),计算参数化建模方法创建的模型与在Creo中创建的模型间的平均相对误差值γ,结果如图8所示。

图8 不同模型的接触应力分布对比
由图8可知两种方法建立的模型应力分布情况基本相同,出现差别的原因可能与模型导入、导出时精度下降有关。相似的方法可以求得其他条件下参数化建模方法创建的模型与在Creo中创建的模型间的接触应力分布平均相对误差值γ,其结果见表6。
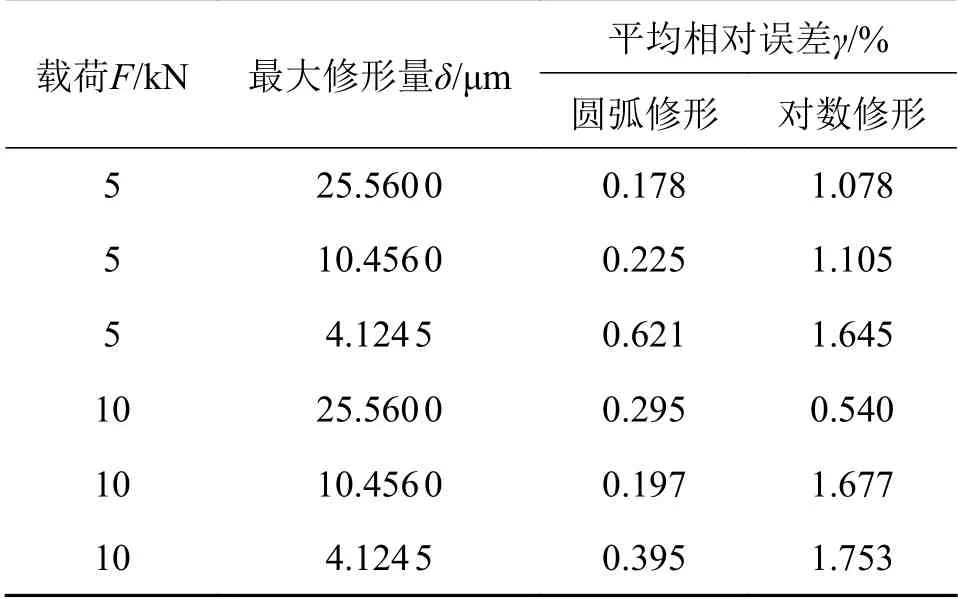
表6 两类模型的接触应力分布平均相对误差值
由表6可知无论是何种修形方式、修形量及何种载荷条件下,参数化建模方法创建的模型与在Creo中创建的模型间的接触应力分布曲线平均相对误差均小于1.8%,说明该参数化方法创建的修形圆锥滚子轴承模型具有较高的准确度。
4.2 建模时间对比
同样以32310圆锥滚子轴承为例,滚子修形方式选择圆弧修形,滚子个数16,对整个参数化建模、改模时间进行研究,得到建立及修改各部分模型所需时间如表7所示。
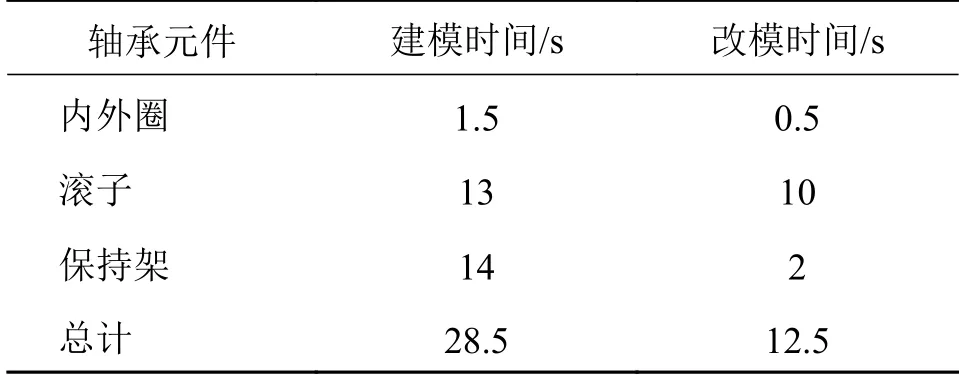
表7 32310轴承各部分建模/改模时间
对于不同配置的计算机,上述时间会有些许差异,但在Creo中创建相同的轴承模型所耗费的建模时间均超过两小时,故对比可知通过该参数化建模方法仍然可以极大的降低工作强度,提高工作效率。
5 结论
1)参数化建模时可将较为复杂的修形圆锥滚子分为修形部分、主体部分及球端面,进而简化了修形滚子的数学模型,提高建模效率。
2)对于圆弧修形和对数修形,在不同修形量及载荷条件下,使用该参数化建模方法创建的修形圆锥滚子轴承模型与在Creo中创建的模型相比,两者接触应力分布曲线的平均相对误差均小于1.8%,验证了该建模方法的准确性。
3)对使用该参数化建模方法的建模、改模时间进行研究,结果表明相对于传统建模方法,该参数化建模方法可以快速完成修形圆锥滚子轴承的三维模型创建,极大的降低工作强度,提高工作效率。
