均衡聚类市场拍卖机制的异构无人机集群任务规划方法*

2022-12-02郑建华

国防科技大学学报 2022年6期

潘登，高东，郑建华

(1. 中国科学院国家空间科学中心复杂航天系统电子信息技术重点实验室, 北京 100190; 2. 中国科学院大学, 北京 101407)

近十几年，随着相关技术的突破和发展，无人机群协同合作完成任务成为无人机领域研究的热点和趋势。在任务环境日益复杂、任务规模日趋扩大、任务内容日渐多样的趋势下，无人机集群任务规划问题的规模和复杂性也在不断增加[1]。若缺乏科学高效的决策和规划，不仅无法体现出无人机集群的优势，还会因为无人机之间在任务、时间、空间上的冲突导致资源浪费甚至任务失败。为此，需要根据任务需求、环境约束和无人机平台特性等，进行科学高效的任务规划，确定各无人机的任务计划和飞行计划，以提高整体执行任务的效能。这就是研究无人机集群任务规划的意义所在。

无人机集群任务规划问题从属于多机器人任务规划问题(multi-robot task allocation，MRTA)，根据任务是否全部已知分为静态任务规划(static MRTA，S-MRTA)和动态任务规划(dynamic MRTA，D-MRTA)[2]。目前大部分无人机集群静态任务规划的研究都是针对特定场景建模，任务类型或无人机种类单一，存在规模较小、通用性不足的问题。部分学者对大规模复杂集群任务规划问题做了研究，文献[3-7]通过聚类的方式，将任务划分成多个任务簇，再将任务簇分配给无人机个体，有效降低了大规模任务规划问题的解算难度；文献[8-11]通过无人机联盟的方式解决异构无人机的任务规划问题。

另外，集群任务规划的研究大多集中在最小化整体成本上，而较少把重点放在提高无人机群的利用率上，即平衡无人机之间的负载。事实上，无人机群在任务中的负载均衡对降低任务总时间和动态任务规划有重要意义。无人机的消耗一方面用于执行任务，一方面用于往返任务地点，两者均对无人机的负载均衡程度有较大影响。一些学者对移动机器人或无人机群任务规划的负载均衡做了研究。文献[3]通过均衡移动机器人个体之间的路程长度，最小化完成任务的总时间，但任务规模较小且不考虑机器人执行任务的消耗。文献[5]先使用K-means法进行任务聚类，再将任务簇分配给各机器人，使旅行消耗达到最均衡，但其聚类过程中没有考虑任务时序、任务代价和出发位置的影响，影响了均衡效果，且其解算使用的穷举法不适用于大规模的任务规划问题。文献[7]先通过限制簇内任务数量、缩短簇内任务距离来保证任务簇之间的负载均衡，再将任务簇分配给机器人组成联盟，这种方式在聚类阶段未考虑任务类别以及出发位置对负载均衡的影响。文献[2]通过引入旅行商问题先确定任务时序和路径，然后将路径碎片化再分配给移动机器人个体，从而将任务时序和路程消耗纳入规划中，在负载均衡分配方面有较好表现，但其先规划路径的方式可能会造成较高的旅行成本。以上方法一定程度改善了任务规划中无人机群的负载均衡程度，但在通用性、均衡程度和降低整体成本方面还有更进一步的空间。

本文提出了一种基于均衡聚类市场拍卖机制的任务规划方法(task planning based on balanced clustering market auction mechanism，BCMA)，目的是解决无人机领域的全局集群任务规划问题，适用于存在合作型任务、异构无人机群以及多出发位置的复杂任务场景。该方法结合了任务聚类和无人机联盟两种策略的优势，降低了大规模异构无人机集群任务规划问题的解算难度，且在形成任务集合的时候就已规划好任务时序；深度融合K-means法的迭代机制与市场拍卖机制，并在市场拍卖机制中引入自适应平衡参数，将路程代价和任务代价同时纳入考虑，形成一种不只考虑空间距离的聚类方法，保证了无人机群的负载均衡。仿真结果表明，本文的任务规划方法能够快速完成较大规模的异构无人机集群任务规划，且规划结果在总消耗、总时间和负载均衡上都有较好的表现。

1 任务规划问题描述

大规模异构无人机集群任务规划的复杂性体现在以下几点：

1)任务数量多，任务需求复杂，不同任务的需求不同，一个任务可能需要具备不同能力的无人机合作完成。这组相互合作完成同一个任务的无人机称为无人机联盟。

2)无人机数量多，且无人机挂载资源的种类和能力不同，一架无人机可能参与多个任务。这组任务称为任务集合。

3)任务地理范围广，存在多个出发位置(地面站)，各站点储备的无人机平台资源量不同。对于执行远距离任务的无人机，前往任务地区的路程消耗不可忽视。

任务规划的目的是将所有任务分解并分配给适合的无人机，确定各无人机的任务计划，同时最优化整体效能。引入任务集合和无人机联盟的机制后，任务规划则需要形成合适的任务集合和无人机联盟，并将任务集合分配给无人机联盟，形成任务计划，示意图如图1所示。

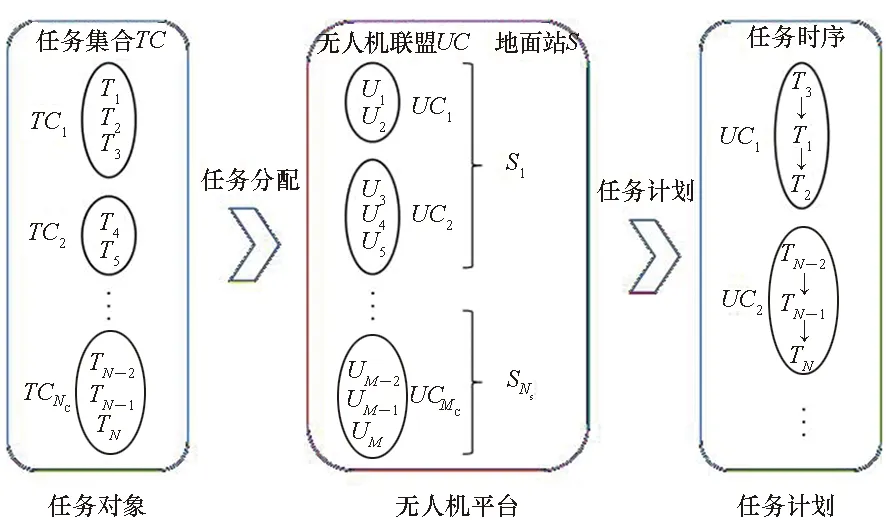
图1 无人机集群任务规划示意图Fig.1 Task planning of UAV swarm

1.1 任务对象

任务对象由N个位置不同的任务目标组成，完成任务需要的平台资源共m类，可分为消耗性资源(例如电量、耗油量、炮弹量)和重用性资源(例如相机、雷达)，假设有m1种消耗性资源和m2种重用性资源。使用重用性资源的同时，一般会额外使用一定量的消耗性资源，例如使用雷达功能需要消耗额外电量。任务总集合

T={Ti|i=1,2,3,…,N}

(1)

任务属性RT可由一个二元组来表示：

RT{Position,Cost}

(2)

RT={RTi|i=1,2,3,…,N}

(3)

RTi={PTi,CTi}={(xTi,yTi,zTi),(CTsi，CTri)}

(4)

式中：PTi(xTi,yTi,zTi)为任务i的位置坐标，CTi为执行任务i的任务代价，包含所需平台资源种类和数量；CTsi、CTri分别为执行任务i的消耗性资源和重用性资源。

(5)

(6)

根据任务规划，所有任务通过聚类形成了NC个任务子集合。任务子集合的集合

TC={TCi|i=1,2,3,…,NC}

(7)

任务子集合属性RTC可由一个二元组来表示：

RTC{Position,Cost}

(8)

RTC={RTCi|i=1,2,3,…,NC}

(9)

RTCi={PTi,CTCi,WCTCi}

(10)

式中：PTi为任务子集合i中执行的第一个任务的位置坐标；CTCi(CTCsi，CTCri)为无人机执行任务子集合i中所有任务的任务代价，包含所需平台资源种类和数量，CTCsi、CTCri分别为执行任务子集合i的消耗性资源和重用性资源；WCTCi为一架无人机按照规划的任务时序完成任务子集合i的路程代价。

1.2 无人机平台

无人机平台由Ns个地面站和M架具有不同资源的无人机组成。无人机平台具有的资源共m类，与任务所需平台资源的种类对应。地面站集合

S={Si|i=1,2,3,…,Ns}

(11)

式中，Si(xSi,ySi,zSi)为地面站的位置坐标。无人机集合

U={Uj|j=1,2,3,…,M}

(12)

无人机属性RU可由一个二元组来表示：

RU{Position,Resource}

(13)

RUj={PUj,SUj}={(xUj,yUj,zUj),(STsj，STrj)}

(14)

式中：PUj(xUj,yUj,zUj)表示无人机j的位置坐标，SUj表示无人机j具有的资源种类和数量；STsj、STrj分别为无人机j具有的消耗性资源和重用性资源。可根据实际情况设置重用性资源转化为某消耗性资源的比例系数。

(15)

(16)

无人机根据任务规划组成MC个无人机联盟，假设同一联盟中无人机均属于同一个地面站，任务过程中作为一个整体行动。无人机联盟集合

UC={UCj|j=1,2,3,…,MC}

(17)

无人机联盟属性RUC可由一个二元组来表示：

RUC{Position,Resource}

(18)

RUC={RUCj|j=1,2,3,…,MC}

(19)

RUCj={PUCj,SUCj}

(20)

式中：PUCj为无人机联盟j所属地面站的位置坐标，SUCj(SUCsj，SUCrj)为无人机联盟j具有的资源种类和数量，SUCsj、SUCrj分别为无人机联盟j内所有无人机的消耗性资源和重用性资源总和。

1.3 约束条件

为了保障无人机群在执行任务过程中的协同，对所建立的模型添加一定的约束条件。定义任务分配决策矩阵XMC×NC，Xji为矩阵第j行、第i列的元素，其意义如下：

(21)

对于任意一个任务集合，只能被某个无人机联盟执行一次；所有的任务都需要被执行，即

(22)

(23)

(24)

执行所有任务的代价不得超出无人机群的总资源。无人机是否还具有执行任务的能力通常取决于两方面：一是续航时间，也就是消耗性资源中的能源量，设置为STsj(1)；二是除能源量以外的消耗性资源，例如炮弹量。由于初步判断的时候任务时序和路程都未知，无法得到准确的路程代价，因此需要保持一定的资源余量，使用α表示资源富余的程度，式(25)表示了总任务代价与无人机群总资源的约束关系。α实际代表任务过程中，任务代价占无人机总资源的比例，可根据无人机的特性设置。ηk为第k种重用性资源CTrk转化为能源量STsj(1)的比例系数。

(25)

例如，图2为经纬M300不同负载(重用性资源)和空载时的飞行时间[12]，最大负载时的续航时间约为空载时的56%，即表示经纬M300约44%的能源消耗在任务负载上。根据经纬M300及市面上一些无人机的情况，本文中α设定在0.5。

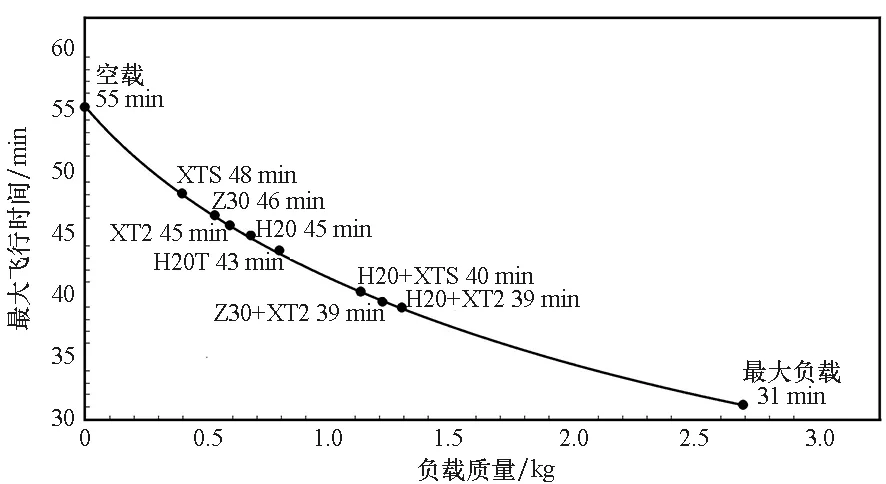
图2 经纬M300飞行时间Fig.2 Flight time of Matrice 300

1.4 规划目标

评估任务规划结果优劣的指标包括：①总消耗CostAll，包括执行所有任务的任务消耗和各无人机从出发到返回地面站的路程消耗；②任务完成率TAR，虽然初始判断的时候保留了一定资源余量(式(25))，规划完成后，仍可能会出现完成任务子集合的总消耗高于对应无人机联盟的总资源，这种情况下会有部分任务无法完成；③总时间ET，假设所有无人机同时出发，以耗时最长的无人机联盟回到地面站的时间作为总时间；④无人机群负载均衡程度μave，使用各无人机联盟资源利用率的标准差表示，μave越小表示负载均衡程度越好。

任务规划的目标如下：

(26)

(27)

其中，UTave为无人机联盟的平均资源利用率，NUCj为任务子集合i对应联盟j的无人机数量，NTCi为任务子集合i的任务个数，NTCFi为任务子集合i能被完成的任务个数，ETj为无人机联盟j完成任务回到地面站的时间。

2 基于均衡聚类市场机制的任务规划算法

无人机集群任务规划本质是解决一个复杂的多目标优化问题[13]，常用的任务规划方法有：传统数学规划法、基于市场机制的方法、基于图论的方法和智能优化算法(如蚁群算法、遗传算法、禁忌搜索算法)等。基于市场机制的拍卖算法最早由Bertsekas提出[14]，模拟人类交互中常见的拍卖行为，通过信息互相共享和传递得到分配方案。市场拍卖算法因其高时效性和分布式结构，被广泛应用于无人机的任务分配问题[15-18]。

市场拍卖算法的基本流程[19]：拍卖者生成一个商品拍卖轮次方案，按照方案顺序发布合同；竞标者分别计算竞拍商品的收益和代价等信息，作为竞拍依据并反馈给拍卖者；拍卖者根据收到的竞标信息选择中标者，并向中标者发布合同；循环直至拍卖轮次结束，所有商品都被竞拍完毕。

在基于市场拍卖算法的无人机集群任务规划中，被拍卖的商品是无人机执行的任务，竞拍者为无人机。竞拍完成则所有任务被划分为多个任务集合分配给参与竞拍的无人机联盟，从而形成了整体的任务规划方案。然而，单纯的市场拍卖算法一方面受到拍卖顺序的影响，其任务规划结果具有很大的随机性，效果无法得到保证；另一方面，虽然可以通过在竞拍依据里引入任务代价均衡，使得规划结果的任务代价趋向均衡，却没有办法引入路程代价，也就无法真正保证无人机群的总负载均衡。

因此本文提出BCMA任务规划方法，将K-means法的聚类迭代机制和市场拍卖算法融合，将路程代价和任务代价通过平衡参数引入市场拍卖算法中，使由市场拍卖算法形成的规划结果能够在迭代中逐渐优化。BCMA任务规划方法的算法流程如图3所示，基本思想如下：

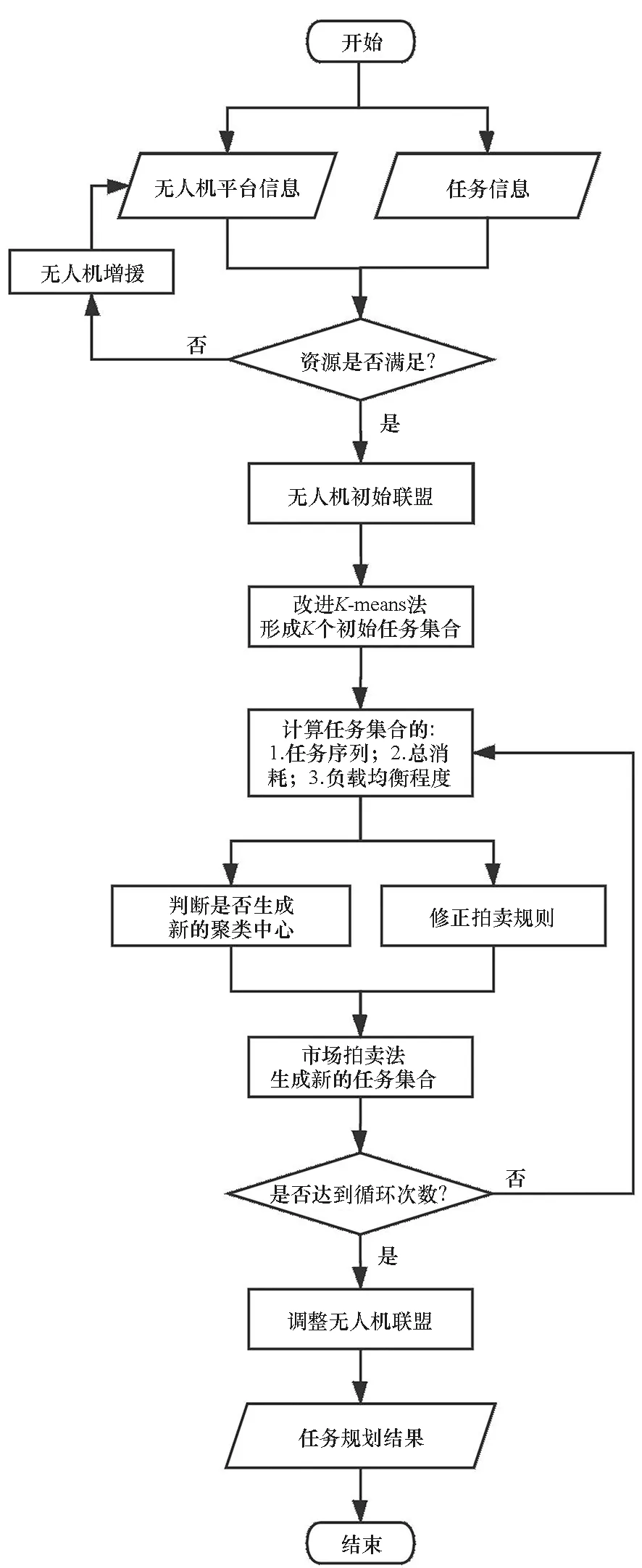
图3 基于均衡聚类市场拍卖机制的任务规划算法流程Fig.3 Task planning algorithm flow based on balanced clustering market auction mechanism

1)根据异构无人机群的分布式结构或资源类型，初始化无人机联盟的数量和组成，使每个联盟的资源总量和比例基本相同。任务所需各类资源的总量决定各类无人机的数量(式(25))，各类资源的比例决定无人机联盟内异构无人机的组成比例。初始联盟数量在可选范围内尽可能多，即在保证联盟能力全面的同时，最小化联盟规模。

2)使用改进K-means法生成初始聚类中心，形成初次规划方案。

3)从第二次迭代起，无人机联盟通过逐一拍卖的方式，将任务聚类形成多个任务集合。

4)拍卖完毕后，通过评估任务集合的负载均衡程度，修正拍卖依据中的平衡参数并判断是否使用更新聚类中心。如需更新聚类中心，使用K-means法生成新的聚类中心。

5)重复步骤3、4直至迭代结束。得到历史最优的规划方案，根据该方案中联盟的任务完成情况，对无人机联盟进行调整保证任务完成率。例如某无人机联盟的任务完成率不到100%,表示该联盟具有的资源不足以完成整个任务计划。根据其缺少的资源类型和数量，给该联盟增加具有对应资源的无人机，增加的数量根据资源缺少量来确定。

2.1 均衡市场拍卖机制

保证无人机联盟负载均衡的核心在于市场拍卖过程的竞拍依据P考虑了各无人机联盟之间的资源消耗均衡程度。定义Pj为联盟j对当前被拍卖任务的竞拍依据，Pj由路程增量代价Di、任务均衡代价Cj以及平衡参数β组成，如式(28)所示。给出最小P的无人机联盟即为中标者，获得被竞拍任务。

Pj=Di+β×Cj

(28)

路程增量代价Di：由于拍卖时任务集合还未完全形成，无法获得准确的路程代价增量，故定义当前被拍卖任务到任务集合i聚类中心的距离为Di，作为衡量路程增量代价的参数。Di越大，则Pj越大，该联盟竞拍到任务的可能性就越小。

任务均衡代价Cj：定义无人机联盟j当前拍卖到的任务总资源与各联盟平均任务资源的差值为Cj，作为任务均衡代价。Cj越大，则Pj越大，任务被分到联盟j对应的任务集合i的可能性就越小。

由于路程增量代价和任务均衡代价属于不同性质的决策因素，需要通过一定的方式转化到同一衡量体系。1.3小节中提到，无人机执行任务的能力取决于两方面，一是能源量，二是除能源量以外的消耗性资源。将路程增量代价和任务均衡代价转化到能源量这一体系中。

路程增量代价通过比例系数η直接转化为能源量(见式(29))；任务均衡代价中的重用性资源部分，通过比例系数ηk转化为能源量，比例系数根据实际情况而定，不同的重用性资源比例系数不同；任务均衡代价中的除能源量外的消耗性资源按对应任务数量占比λk并入能源量中(见式(30))。

(29)

式中，(xnew,ynew,znew)为当前被拍卖任务目标的位置坐标，(xi,yi,zi)为任务集合i的聚类中心坐标，η为路程转化成能源量的比例系数。

(30)

式中，ΔSUCj为联盟j完成当前已拍卖到的任务所需的能源量与各联盟平均的差值，λk为使用第k种消耗性资源的任务数量占比，ηk为使用第k种重用性资源转化为能源量的比例系数，Cj(k)为无人机联盟j当前已拍卖到的任务所需第k种重用性资源与各联盟平均的差值。

因为Di仅为路程增量的估计值，没有考虑任务时序和多出发位置的影响，故引入平衡参数β。每次迭代中任务拍卖完成后，分别计算每个任务集合使路程最短的任务时序，进一步求得无人机联盟之间的负载均衡程度μave。如果μave同比上次迭代增加较多，说明本次迭代效果不理想，选择不更新聚类中心，并适当增大平衡参数β，使下次迭代中均衡程度的影响变大；反之，则更新聚类中心，并适当减小β，以增大拍卖算法的探索范围。

(31)

式中，β初值设为0.6，算法会根据负载均衡程度自动调整β，在一定范围内β初值对计算结果没有明显影响。μave_old为上一次规划结果的负载均衡程度，γ为判断μave过大的阈值。图4所示为不同数值的γ对算法收敛时的迭代次数的影响，根据该图将γ设为1.2，使算法在各种情形下都能较快达到收敛。

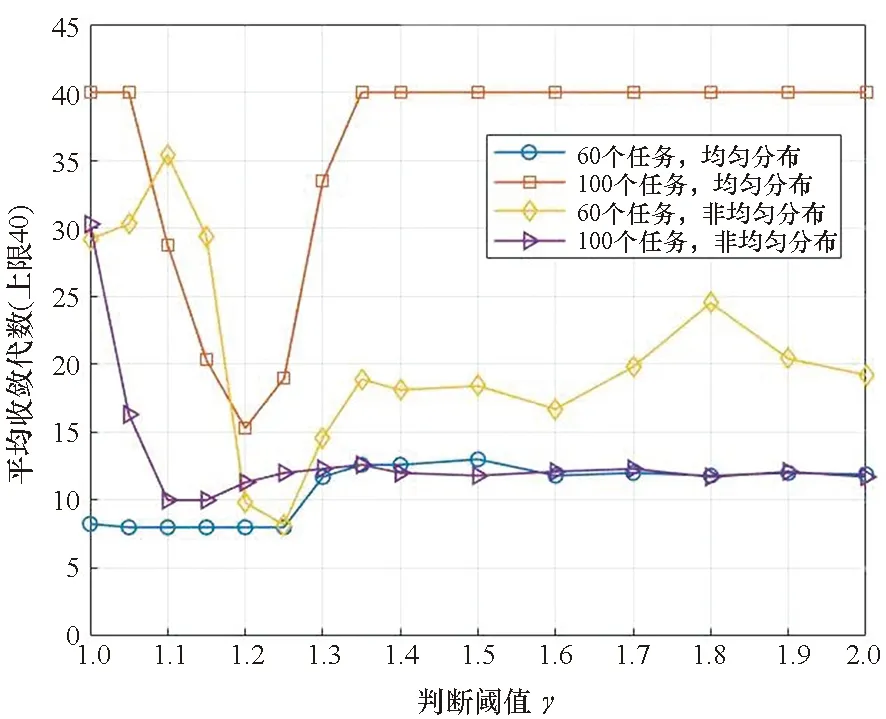
图4 判断阈值γ对算法收敛的影响Fig.4 Influence of judgment threshold γ on algorithm convergence

2.2 LKH-2算法求解旅行商问题

为获得无人机联盟的负载均衡程度μave，需要在每次形成任务集合后，分别计算各个任务集合使路程最短的任务时序，这是典型的旅行商问题(travelling salesman problem, TSP)。BCMA任务规划方法需要解算较多次数的旅行商问题，旅行商问题的求解速度是影响算法效率的最大因素。

本文使用LKH-2算法对旅行商问题进行求解。LKH-2算法是一种启发式局部搜索算法，是目前求解对称旅行商问题的最优或近似最优解最成功的方法之一。Helsgaun于1999年提出LKH(Lin-Kernighan heuristic)算法[20]，是当时除穷举法外精确度最高的旅行商问题搜索算法，且收敛速度较快[21]。2009年，Helsgaun进一步改进LKH形成LKH-2算法[22]，使其更适用于求解大规模的旅行商问题。

为了验证LKH-2算法适用于求解本文任务规划中的旅行商问题，使用TSPLIB[23]中已知最优解(最短路程)的部分中小型规模问题作为LKH-2算法的检验样本,TSP编号名称中包含的数字即为城市数量。对每个样本进行100次重复试验，仿真结果见表1。

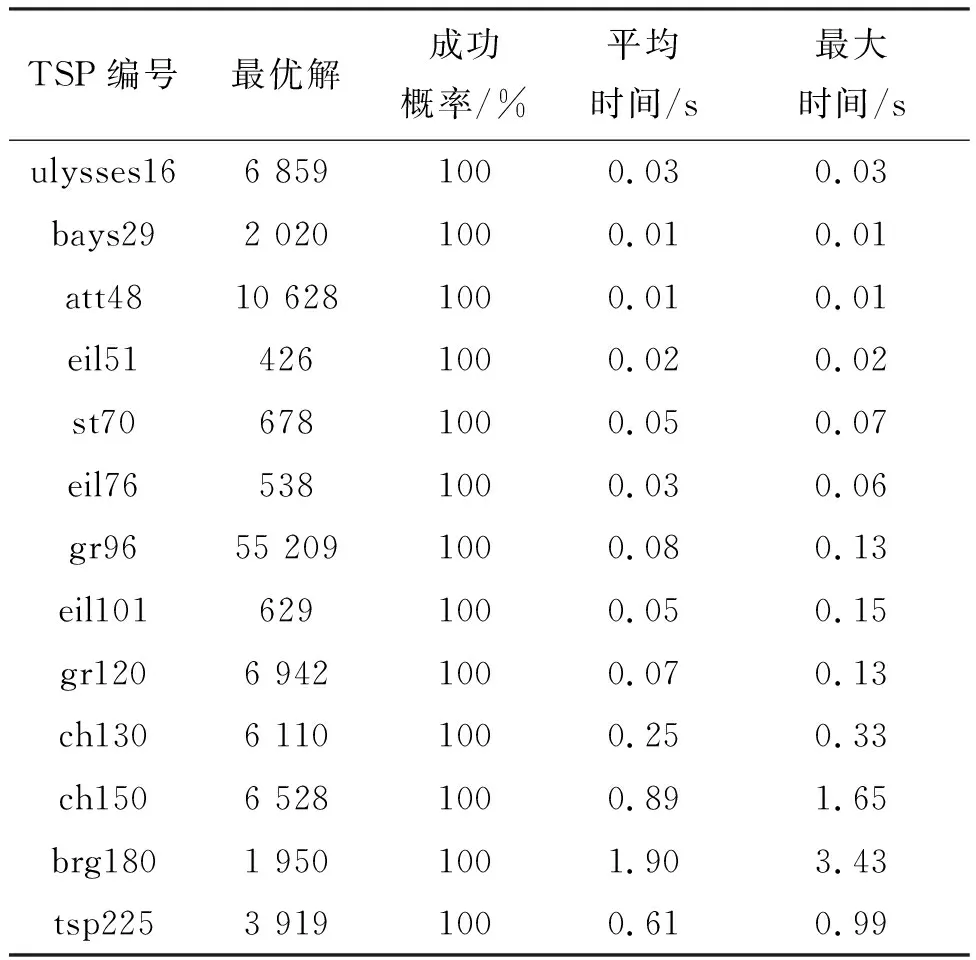
表1 LKH-2算法检测结果

由表1可知，LKH-2算法随着城市数量的增多，其解算时间整体呈上升趋势。在解算100个城市以内的旅行商问题上，单次解算速度基本稳定在0.1 s以内，且都能达到最优解。在解算50个城市以内的旅行商问题上，单次解算速度基本稳定在0.03 s以内。例如某次任务规划中，迭代20次，需要形成5个任务集合，每个集合内的任务数量不多于50个，则整个过程需要求解100次旅行商问题，解算时间1～4 s。因此，使用LKH-2算法求解旅行商问题能够保证本文任务规划方法的时效性。

2.3 任务聚类中心的形成和更新

K-means算法是任务目标聚类最常用的算法[3-5,13,24]，通过迭代反复修改聚类中心和聚类来达到最满意的聚类结果，具有计算简单、能快速处理大数据集等优点。传统K-means算法的初始聚类中心是从数据对象中随机选取的，但K-means算法对初始聚类中心敏感，不同初始中心对应的聚类结果可能有很大的区别[25]。为了保证聚类效果，不至于出现某些任务簇内无任务的情况，将初始聚类中心尽可能分散[7]。

已知任务目标集合T,定义任务聚类中心集合CL,需要生成的聚类中心数量NTC，任务目标Ti和Tj之间的欧氏距离为DT(i,j)；k为CL中已有聚类中心的个数,初值为0；SD(j)为T中第j个任务到CL中所有聚类中心的距离之和，则有

DT(p1,p2)=maxDT(i,j)，i∈[1,N]，j∈[1,N]

(32)

(33)

SD(pk+1)=maxSD(j)，j∈[1,N-k]

(34)

如果NTC=2，选择Tp1和Tp2作为初始聚类中心；如果NTC>2，先将Tp1和Tp2任务从T中抽出放入CL中，然后在T中抽取使SD最大的任务Tpk+1，作为新选取的聚类中心放入CL中。重复该抽取过程直至CL中的聚类中心个数k等于NTC，至此完成初始聚类中心的计算。

根据各地面站具有的无人机联盟数量比例，将聚类中心按该比例和到各地面站距离分配给合适的地面站。表2所示为一次聚类中心分配的示例，计算得到的6个聚类中心CL1～CL6需要分配到3个地面站S1～S3，三个地面站的无人机联盟数量比例为3 ∶1 ∶2，即表示三个地面站分别匹配3、1、2个聚类中心。按照聚类中心编号顺序，分配该聚类中心到距离最近的地面站，如该地面站已经满员，则按照距离从近到远往后顺延。这种分配方式不一定能达到最优解，但过程简单，能够满足初次分配的需求。

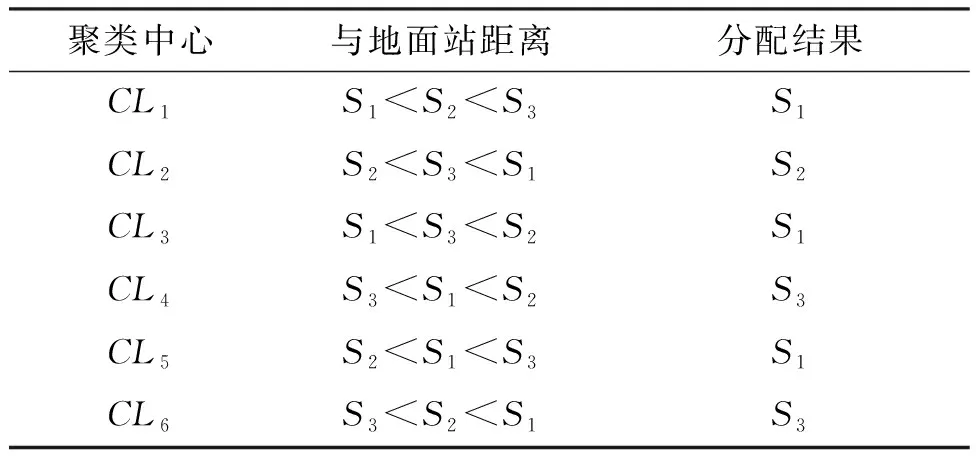
表2 聚类中心分配示例

聚类中心的更新机制与K-means算法一致，即新的聚类中心为该任务簇中所有任务目标坐标的均值。通过这种更新机制，能够完成对数据空间比较全面的快速搜索。

图5为一次基于均衡市场拍卖机制的任务规划中，总消耗CostAll和负载均衡程度μave随迭代次数的变化。可以看出，本文的BCMA法在迭代中，能有效抑制μave的突增，同时使CostAll整体呈下降趋势。

(a) 总消耗随迭代的变化(a) Total cost with iteration

3 仿真实验

设置任务目标范围1 000×1 000，有两个位置不同的地面站S1(300,300)和S2(700,700)。平台资源的种类有四种，其中一种为消耗性资源CTs1，假设为电量；三种为重用性资源CTri(i=1，2，3)，假设分别为可见光传感器、红外传感器、激光探测仪。任务数量N取40～150，位置在规定范围内随机生成，所需无人机到达任务目标位置即完成任务。完成某个任务需要1～3种重用性资源，即可能需要多架异构无人机合作完成。无人机数量M为12～45，单架无人机的初始CTs1=10 000，具有重用性资源中的一种，每使用该种功能完成一个任务需消耗200的电量，即ηk=200。路程转化成消耗性资源的比例系数η=1。S1和S2两个地面站的无人机数量比例为1 ∶2，具有三种重用性资源的无人机比例为1 ∶1 ∶1。

以文献[7]中GCABTD算法的簇内相互距离和为聚类依据的改进贪婪聚类算法，在负载均衡方面有很好的表现。使用本文BCMA算法、K-means算法和改进贪婪聚类算法对不同规模和特点的异构无人机集群任务规划进行对比仿真实验。为使无人机联盟功能全面，初始联盟由3架具有不同资源的无人机组成。仿真结果为调整无人机联盟之前的规划结果，故可能存在任务完成率小于100%的情况。这种情况下需要根据资源缺少情况调整无人机联盟，以保证所有任务完成。

3.1 任务目标均匀分布

任务目标数量N取40～150，以10为间隔，位置在全地图随机生成，每个任务所需资源种类随机生成，控制需求每种资源的任务数量占总任务数量的2/3。对应无人机数量M取12～45，间隔为3。重复试验100次，并计算平均的任务完成率TAR、总消耗CostAll、总时间ET和负载均衡程度μave。总时间ET由最长路程的长度表示，不考虑执行任务所需时间。仿真结果如图6所示，其中总消耗、总时间和负载均衡程度的显示以K-means法为基准(优于/劣于K-means法的百分比)。

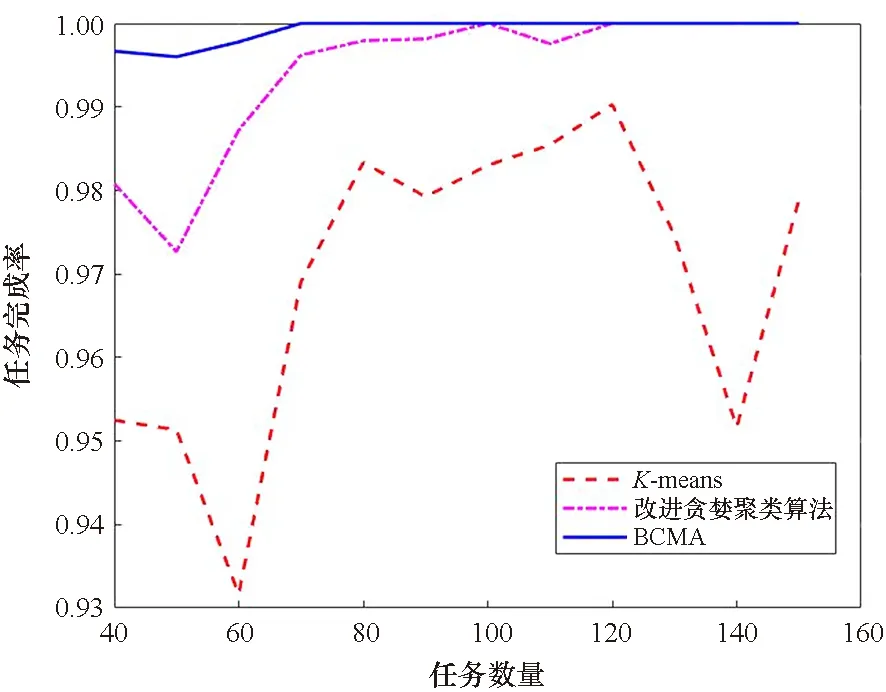
(a) 任务完成率(a) Task accomplishment ratio

在任务均匀分布的情况下，本文的BCMA法在任务完成率上优于K-means法和改进贪婪聚类法，且随着任务规模的增大而趋于100%。在总消耗和总时间上，BCMA法相较改进贪婪聚类法更有优势。改进贪婪聚类法随着任务规模的增大，负载均衡程度逐渐改善，规模较大时与BCMA法效果近似甚至略优于BCMA法。K-means法在任务均匀分布的情况下，总消耗和总时间表现较好，但负载均衡程度明显较差，且其任务完成率也低于其他两种方法。

图7所示为任务数量N=60，无人机数量M=18，分为6个任务集合、任务均匀分布的情况下，K-means法、改进贪婪聚类法和本文BCMA法的一次任务规划结果。五星代表地面站位置，圆点代表任务位置，菱形代表聚类中心/聚类起点，回环代表无人机联盟完成任务的路线。

从图7可以看出，在任务均匀分布的情况下，K-means法和BCMA法的聚类中心比较分散，集合内的任务也相对集中，因此路程长度较短，路程消耗和总时间都比较少。而改进贪婪聚类法的任务集合重叠较多，路程较长，所以在总消耗和总时间上表现较差。K-means法各任务集合中的任务数量差别较大，因此负载均衡程度表现较差。

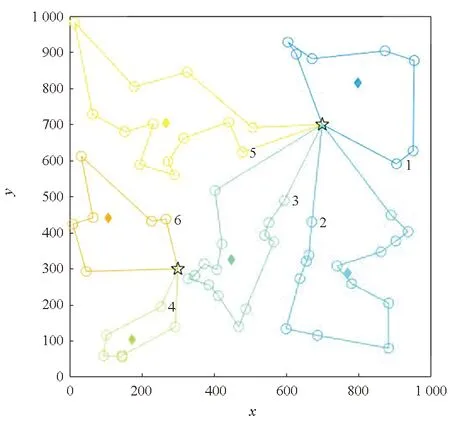
(a) K-means法任务规划结果(a) Task planning results of K-means

3.2 任务目标位置非均匀分布

对任务的分布区域进行限定，其他设置与3.1小节同。图8为任务分布在地图右半区域时的仿真结果。

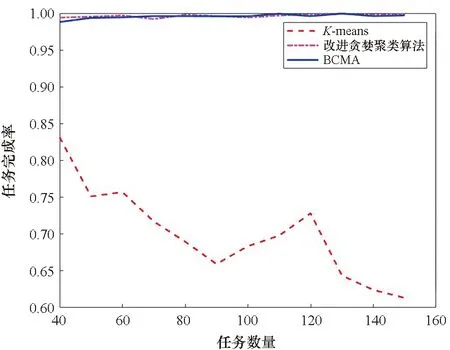
(a) 任务完成率(a) Task accomplishment ratio

仿真结果表明，对于任务位置非均匀分布的情况，本文的BCMA法和改进贪婪聚类法的规划效果比较相近，在任务完成率都接近100%的情况下，BCMA法在总消耗和总时间上更有优势，但在均衡负载程度上稍差于改进贪婪聚类法。而K-means法由于路程短，路程消耗少，总消耗和总时间是三种方法中最小的，但K-means法的负载均衡程度很差，任务负载较多的无人机联盟无法完成所有任务，且随着任务规模的增大任务完成率进一步降低，不能满足任务规划的需求。

3.3 任务目标类型非均匀分布

任务位置在全地图随机生成，但对任务类型的分布区域进行限定，其他设置与3.1小节同。图9所示为任务位置随机分布，但需求重用性资源CTr3的任务限定在地图左右各1/3区域时的仿真结果。

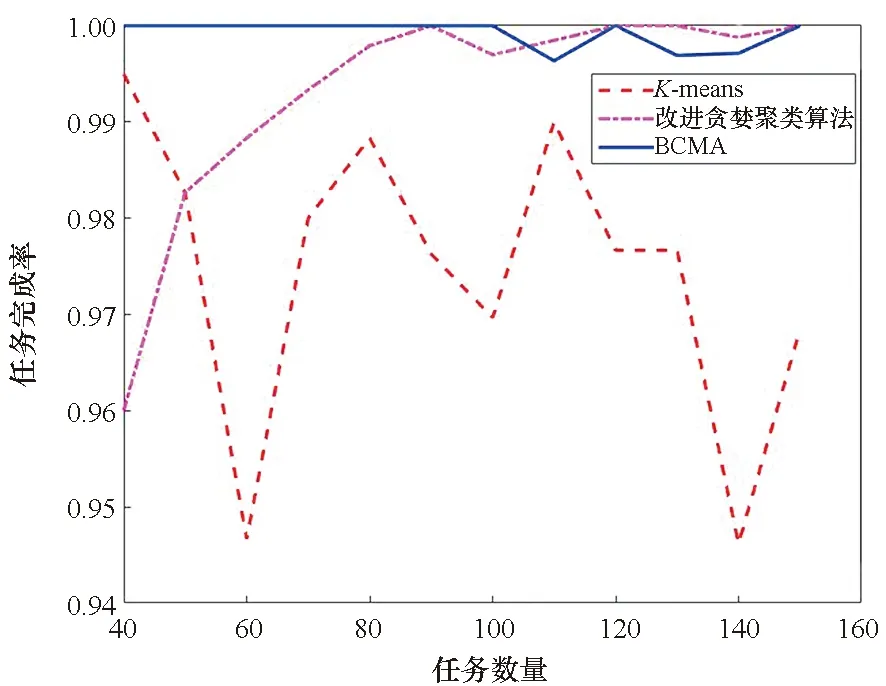
(a) 任务完成率(a) Task accomplishment ratio

由图9可知，在任务类型非均匀分布的情况下，BCMA法和改进贪婪聚类法在任务完成率和负载均衡程度上整体优于K-means法。而在总消耗和总时间方面，从小到大分别为K-means法、BCMA法和改进贪婪聚类法。

3.4 实验结果分析

通过以上仿真实验可知，本文的BCMA任务规划方法适用于不同规模、不同任务分布的全局任务规划。尤其是在任务非均匀分布的情况下，依旧能保持高任务完成率，并在总时间、总消耗和负载均衡上均获得较好的效果。

从仿真结果上看，K-means法的总消耗和总时间表现最佳。然而K-means法总消耗较少，一方面是因为路程短，另一方面是因为其任务完成率较低，部分任务未被执行；其总时间较短，一方面是因为旅行时间短，另一方面则是因为实验没有设置执行任务的时间，未体现任务代价不均衡对总时间的影响。实际上执行任务的时间越长，K-means法负载不均衡对总时间的影响会更容易得到凸显。

另外，BCMA法的任务完成率存在达不到100%的情况，尤其是在任务数量较少的时候。原因在于规划初始，预估的任务代价占比为固定值(式(25)中α)。而当任务数量较少且分布分散时，任务代价占比低于该定值且偏离较多，导致对资源总量的预估低于实际需求量，少量任务无法完成。