地下连续墙支撑开挖监测及数值模拟
2022-12-02吕紫君张安琪
俞 荣,吕紫君,张安琪
(1.南京振高建设有限公司,南京 211300; 2.南京市水利规划设计院股份有限公司,南京 210006)
1 概 述
地下连续墙是保持深基坑开挖稳定性的重要技术之一,在地下连续墙浇筑与基坑开挖过程中,如何确保结构的稳定是岩土工程界十分关注的问题[1-2]。在施工中做好动态的监控量测工作,是保障维护结构稳定性、降低工程风险的有效方式,同时采用数值模拟方法作为变形预测研究也具有重要意义。
为此,国内外学者进行了一系列的研究。Gordon等[3]研究认为,使用常规的土体模型在软土地质环境下研究地铁基坑周边地表沉降以及围护结构的水平位移会存在较大的误差,提出了新的简化半经验软土模型。LoKY[4]通过二维有限元模型,对多伦多市某地铁工程的监测进行了模拟。Zdravkovic等[5-6]研究认为,有限差分法和三维有限元模拟法较二维有限元模拟法更可靠。江轶华[7]等基于小应变硬化土(Hardening soil small strain)模型,采用在单元表面施加荷载边界条件的方法模拟泥浆护壁,建立三维数值模型,模拟地下连续墙施工过程。王进等[8]基于布里渊光频域分析(BOFDA)技术,进行地下连续墙变形现场监测的方法与技术研究, 给出依据分布式光纤监测的应变数据换算地下连续墙变形的计算方法。余平等[9]采用地下连续墙加内支撑的支护方式,采取详细的基坑监测方案。此外,还有学者通过现场测试,采用有限差分软件FLAC3D对基坑变形数据进行比较分析[10-12]。
本文以南京市区某基坑项目为例,通过测斜仪分析开挖过程中地下连续墙的变形趋势,采用数值软件对基坑开挖进行模拟,对比分析莫尔-库仑本构(M-C)模型和硬化土体模型(HS)的计算结果与实测结果之间的差异,研究成果可为相关工程提供参考。
2 工程概况
本次分析的基坑开挖区域位于南京市区,距离街道约30 m,最近的建筑物在20 m以内。由于地下水位较高,根据工程勘察报告,建议基坑开挖时采用厚60 cm的地下连续墙技术。在项目实施期间,这些地下连续墙构成了开挖的挡土结构,并根据设计文件使用墙体设计和结构分析软件进行静态计算。由图1的岩土工程勘察结果表明,在基坑开挖处,土层的顶层(1 m)由人工填土组成,下一层是有机粉土(约5.1 m,分为两个亚层(厚3.3和1.8 m)),强度和刚度参数略有不同),第三层是砂砾石(约7.3 m),而墙底部存在黏土层。开挖是分期施工进行的,并在地下连续墙和钢筋混凝土盖梁完工后开始。
施工时,建造了厚度60 cm、深度16 m的地下连续墙,安装了临时支撑结构,并使用CFA桩为塔式起重机的深基础架设了临时柱,使建筑的其他部分能够按照既定的工作计划在干燥和安全的开挖范围内施工。最终开挖深度约为10.5 m,地下水位在地形标高以下约3 m处。在施工的第一阶段,在地下连续墙内进行挖掘。地下连续墙作为一个挡土结构一直延伸至停车场的一楼,在楼板完工并安装临时支撑结构后,采用自上而下的方法进行开挖。在开挖期间,对地下连续墙进行了详细调查,并通过测量安装在墙体内的测斜仪套管来监测其变形。工程完工后,发现地下连续墙的实测位移低于设计阶段的估计值,这表明与深基坑相关的整个过程所采用的假设是正确的,并且工程计划得到正确执行。
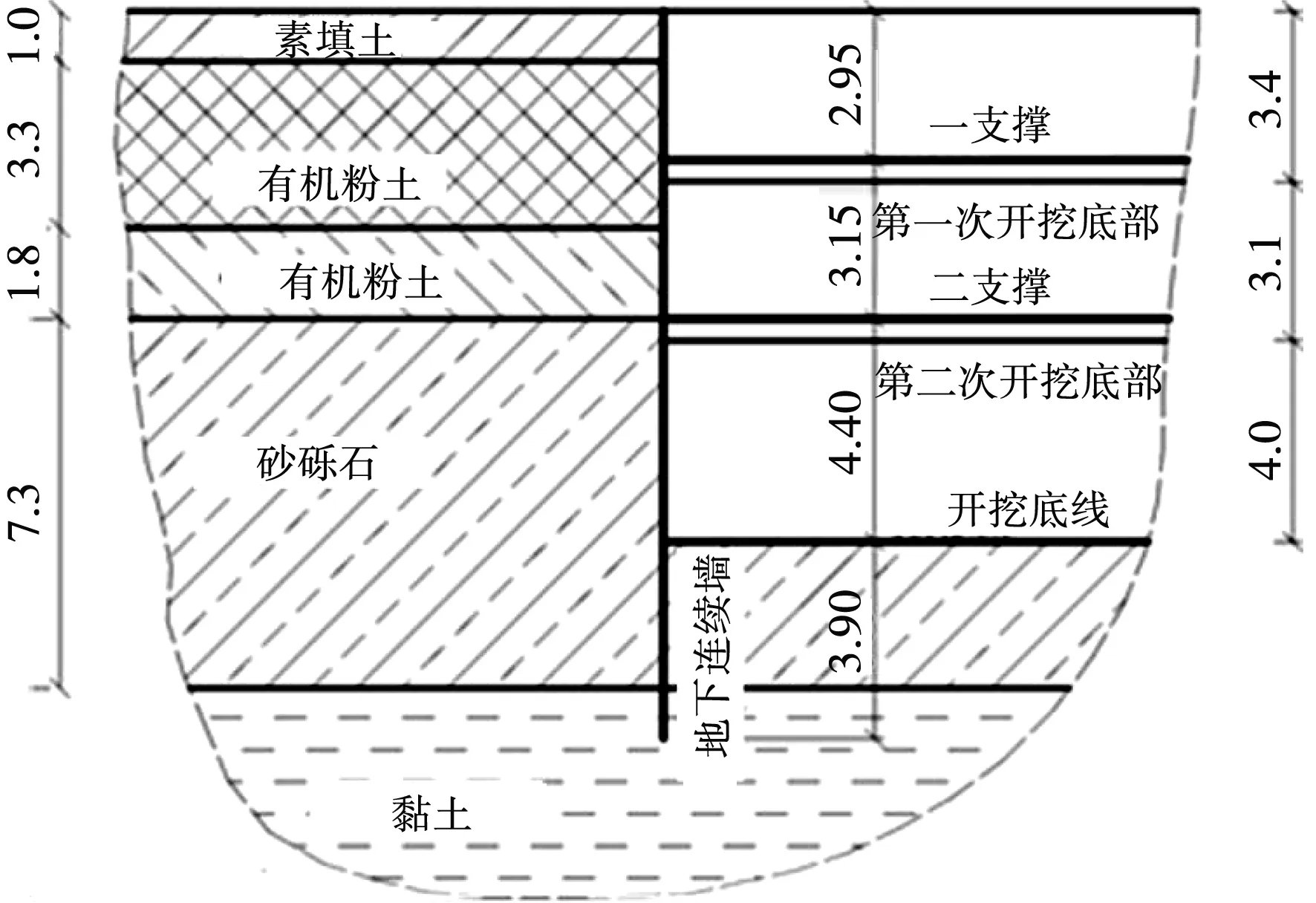
图1 基坑开挖横截参数及施工步骤
3 基坑变形监测
测斜测量的目的是在涉及地下三层地下连续墙内部开挖的施工期间,确定地下连续墙的变形程度。随着基坑工程的开展,地下连续墙逐渐承担由地压引起的荷载,从而导致其发生位移和变形,这些变化通过观察安装在墙体内的测斜仪套管进行监测。本次使用倾斜仪测量每个套管中探头的两个位置,以便能够计算测斜仪偏差和测量误差不超过0.8 mm。每个套管的测量方向A+是朝向开挖的方向,方向B+是沿着监测墙的方向。将测斜仪套管安装在地下连续墙面板内,深度为地面以下15 m,位于预计变形最大的位置。外壳的布置和数量见图2。倾斜监测测量计划在施工的每个阶段结束时进行,第一次在地下第一层开挖完成后进行,第二次在第二层开挖完成后进行,第三次在开挖至最终深度后进行。
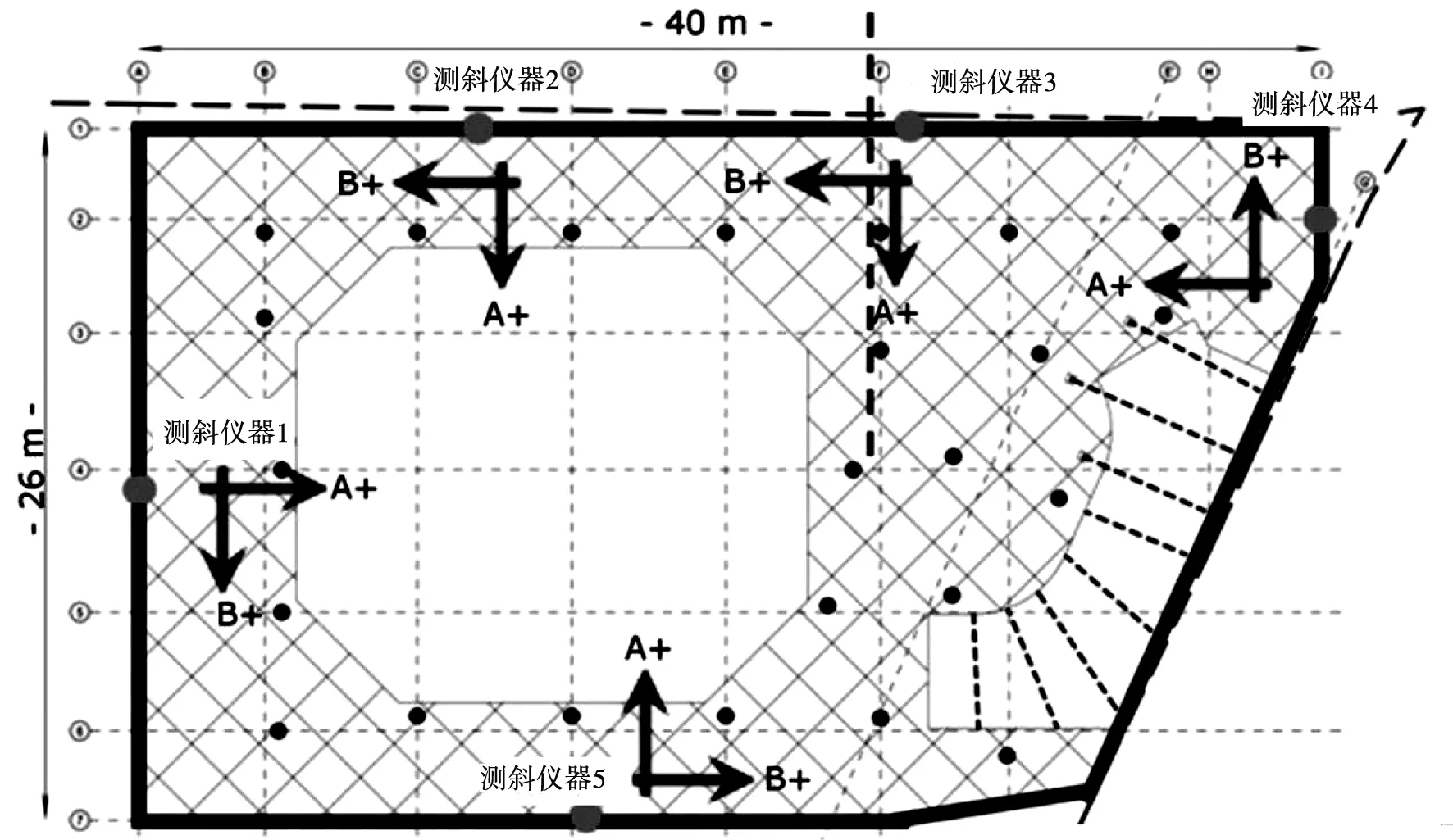
图2 测斜仪的布置及数量
图3为不同施工步骤下地下连续墙累积位移。
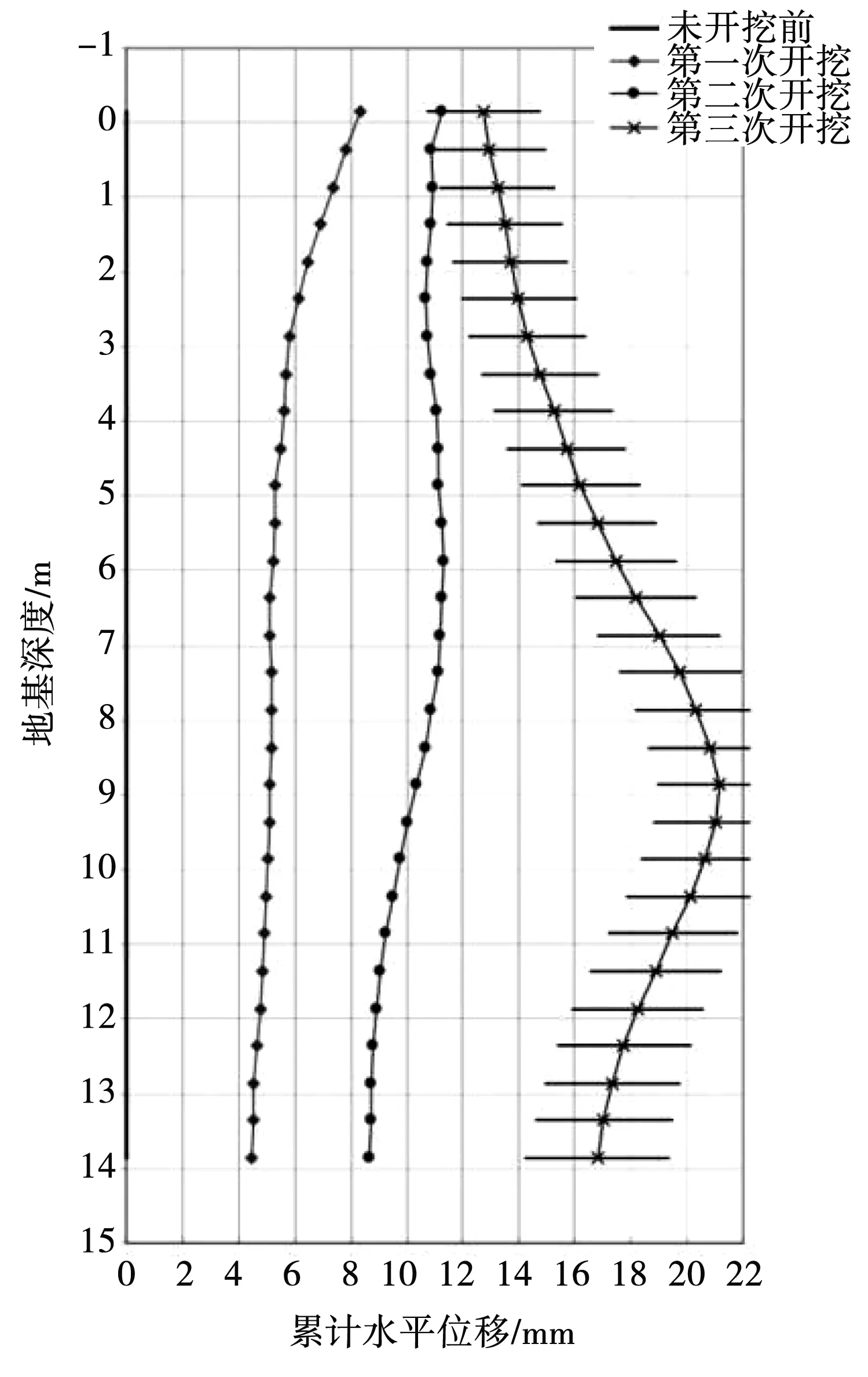
图3 不同施工步骤下地下连续墙累积位移
由图3可知,在基坑未开挖时,地连墙未发生位移变形,保持稳定。当第一次开挖后,整个地基深度内出现明显的位移,在底部14 m处,向右倾斜4 mm,在高程0 m处累计位移最大为8.1 mm;当第二次开挖后,底部14 m处累计位移增大至8.1 mm,而最大累计位移发生位置转移至地基中部,达到11 mm;最后,当地基开挖至底部时,地下连续墙整体累积位移最大,其中在地基底部14 m处,地连墙整体累积位移为17 mm,最大位移在地基深度9 m处,达到21 mm。
4 数值模型建立
本文使用Plaxis 2D软件对挡土系统的性能进行评估。平面应变有限元数值模型包括3个施工阶段,其中包括3个开挖步骤,每步开挖深度与施工时的开挖深度保持一致,还包括安装两个支柱的分析阶段。计算中,采用重力荷载来确定底土的初始应力。土体采用两种本构模型进行计算:一种为具有小应变刚度的硬化土体模型(HS)进行建模;一种为莫尔-库伦本构模型。对于混凝土和钢构件,采用弹性模型。与弹性模型相比,使用硬化土(HS)的优势在于控制刚度参数,包括切线固结仪模量、割线三轴模量E50、卸载-再加载模量。图4为本次建立的数值模型。数值计算参数见表1。

图4 数值模型

表1 岩土计算参数
5 监测与数值结果分析
图5、图6分别为莫尔-库仑模型本构和硬化土本构下,地基开挖引起地连墙位移变化规律。

图5 莫尔-库伦本构下地连墙位移变化
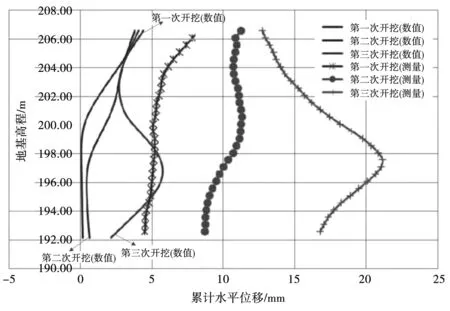
图6 HS本构下地连墙位移变化
由图5可知,对于莫尔-库仑本构(M-C)模型,数值结果与实测结果具有明显的差异。当第一次开挖结束时,二者地墙顶部和底部的位移相差不大,但M-C模型地墙中部的位移不到1 mm,而实测值为4 mm左右;当第二次开挖结束后,二者除地墙底部的位移相差不大以外,其余部分有明显差异,在地墙中部二者最大位移相差5 mm以上;当开挖结束后,数值模拟值与实测值相差最大,达到10 mm左右。因此,使用莫尔-库仑模型计算的结果会高估墙体的水平位移。
从图6中可知,对于HS模型同样可以看到二者的巨大差异,且随着开挖步骤的深入,差异越明显。当第一次开挖结束后,数值模拟与实测的地墙最大位移之差为5 mm;第二次开挖结束后,最大位移之差达到8 mm;当开挖结束后,二者的最大位移之差达到18 mm。由图6可知,墙的数值计算位移和实际测量位移之间有强相关性,因为二者的变化趋势十分相似。HS模型倾向于低估墙体底部的水平运动,这种差异的主要来源是岩土工程勘察的可靠性不高。因此,对于复杂问题(如深基坑),数值模拟方法建议采用硬化土体模型(HS)进行建模,可以用来作为基坑开挖地连墙的初步变形趋势判断。而对于土壤参数的初步估计,建议采用更复杂的方法(例如三轴试验),以便更好地估计土壤参数,以此来提高计算位移和测量位移之间的相关性。因此,不建议使用莫尔-库仑模型估算墙体位移,即使岩土参数的可靠度不是很高,使用硬化土模型也可以获得与监测结果更为一致的结果。
6 结 论
本文以南京市区某基坑项目为例,通过测斜仪分析了开挖过程中地下连续墙的变形趋势,采用数值软件对基坑开挖进行模拟,对比分析了莫尔-库仑本构(M-C)模型和硬化土体模型(HS)的计算结果与实测结果之间的差异。研究成果表明,M-C模型会高估地连墙体底部的水平运动,而HS模型会低估地墙底部位移,这种差异的主要来源是岩土工程勘察的可靠性不高。因此,对于复杂问题(如深基坑),数值模拟方法建议采用硬化土体模型(HS)进行建模,可以用来作为基坑开挖地连墙的初步变形趋势判断。而对于土壤参数的初步估计,建议采用更复杂的方法(例如三轴试验),以便更好地估计土壤参数,以便提高计算位移和测量位移之间的相关性。
