风电机组参与调频的系统频率响应模型

伍双喜，谭嫣，刘思宁，杨银国，李宇骏，刘洋，向丽玲，陆秋瑜，于珍

(1. 广东电网有限责任公司电力调度控制中心，广州510060；2. 西安交通大学电气工程学院，西安710049)

0 引言

近年来全球变暖与能源危机日益加剧，风力发电成为解决上述问题的一种有效手段。目前，变速风机因具有最大风能捕获能力而成为应用最广泛的风机种类[1 - 3]。为了捕获最大风能，变速风机通过电力电子换流器与电网连接，但换流器将电网频率与风机输出功率完全解耦，这意味着变速风机无法像同步机一样对电网的频率波动做出响应[4]。因此随着现代电力系统风能渗透率的不断提升，系统的惯量水平大幅下降，恶化了系统的频率稳定性。为解决这一问题，许多国家要求风机具备频率响应能力[5]。

总的来说，风机有两种参与系统调频的方式。第一种是有备用方式[6 - 7]，即风机运行于减载状态，在频率波动时释放备用功率进行频率支撑。减载的方式有两种，分别是超速减载[6]与桨距角减载[7]。文献[6]利用风机备用功率来承担一次调频并提出根据可用备用容量动态调整一次调频系数的控制策略。但是在减载策略下风机无法实现风能的最大捕获，因此风电场的收益与效率会受到影响。

第二种方法是风机工作在最大风能捕捉(maximum power point tracking, MPPT)方式[8 - 18]，通过释放转子动能来提供频率支撑。当检测到频率波动后，附加控制器启动，从而给风机的输出功率参考值加入一个与系统频率相关的分量，以此模拟惯量响应。这种方法根据采用的附加功率分量可以分为两类。第一类采用正比于频率变化率(rate of change of frequency, ROCOF控制器)或者频率偏移量(下垂控制器)的附加分量[7 - 16]，第二类采用预先定义的附加功率分量[17 - 23]。文献[17 - 18]在频率支撑过程中采用恒定大小的附加功率，文献[19 - 21]则设计了调频附加功率随风机转速下降而减小的控制策略，文献[22]还提出了风机与同步机的协调频率控制策略。

然而，上述关于附加频率控制器的研究都是基于仿真的方法，这种方法只能定性分析频率控制器对系统频率响应的提升作用，要定量解析则需要推导附加频率控制器作用下系统的频率响应模型。文献[24]推导了同步机系统的低阶频率响应模型并给出同步机参数对于系统频率响应的影响。当风机参与频率支撑后，计算系统频率模型需要将风机与同步机的频率响应特性相结合。文献[25 - 26]推导了减载调频方式下系统的频率响应模型，但忽略了风轮机动态对风机输出功率的影响，同时这些频率模型形式较复杂，难以直接解析计算出频率评价指标(系统频率最低点、ROCOF等)。此外，目前也有一些文献考虑了风轮机动态对于风机调频过程的影响，文献[27 - 28]分别给出了减载与MPPT两种运行方式下考虑风轮机动态后风机的频率响应特性，但是都没能将风机的频率响应特性与系统中同步机的特性相结合。文献[29]给出波动风速下系统的频率响应特性，但无法得到解析表达式。

本文推导了风机在减载与MPPT两种工作方式下的系统频率响应模型，同时选取频率最低点作为评价系统频率响应的指标。在减载模式下，系统频率响应的最低点可以通过反拉普拉斯变换的方法计算得出；然而在MPPT下系统的频率模型为三阶，难以直接计算频率最低点。为解决这一问题，本文提出一种模型降阶方法，采用降阶模型计算出了MPPT下的频率最低点，并通过仿真验证了降阶模型的准确性。通过研究风机不同工作方式下系统的频率最低点，可以得到频率控制器参数与频率响应之间的定量关系。

1 系统建模

考虑图1所示的单机系统并对此系统做出以下假设。

1)对于频率稳定性问题线路损耗可以忽略。

2)换流器控制的动态过程可以忽略，因此风机的输出功率与其功率参考值相等。

3)多同步机电网可以等值为单台同步机。

4)在调频过程中风速恒定。

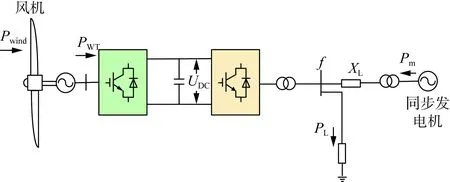
图1 系统拓扑Fig.1 System topology

基于以上假设，系统的频率响应可以写为：

(1)

式中：HG为同步发电机的惯性时间常数；Δf为频率偏移量；ΔPM、ΔPWT和ΔPL分别为同步机功率、风机输出功率以及系统负荷的变化量。惯量响应所研究的时间尺度为受扰后的数秒至数十秒，在这样一个时间段内风速可视为定值，因此风机机械功率为定值。考虑简化的原动机模型为：

(2)

式中：RG为原动机调差系数；FH为汽轮机再热常数；TR为再热时间常数。将式(1)与式(2)联立即可得到系统的频率响应模型为：

(3)

2 减载风机参与调频的系统频率响应模型

为使风机具有频率支撑能力，应在风机功率参考值中加入一个与频率相关的分量，典型的附加分量由正比于频率微分和正比于频率偏差量的两部分组成，但是频率微分分量易受测量过程中噪音的干扰，因此本文仅利用频率偏差量的下垂频率控制，具体的控制结构如图2所示。此时风机的输出功率为：

PWT=PWTref-KWTΔf

(4)

式中：PWT为风机的输出功率；PWTref为风机未进行调频时的功率参考值；KWT为风机频率控制器下垂系数。

图2 风机下垂频率控制结构Fig.2 Structure of the WT droop frequency control

采用下垂频率控制时风机有两种工作方式，分别是减载方式与MPPT，这两种方式的区别在于风机未参与调频时功率参考值PWTref的设定。在MPPT下，PWTref为风机MPPT功率参考值，如图2所示。MPPT功率参考值与风机转速的三次方成正比，而在减载方式下功率参考值则设置为最大风功率乘以一个减载百分数：

Pdel=ηPmax

(5)

式中：Pmax为风机的最大输出功率；h为减载百分比(这里设置为80%)。图3中运行点A点为最优运行点，其功率即为当前风速下风机可捕获的最大功率，B点则是减载运行点。因减载方式下功率参考值PWTref为定值，故调频过程中风机功率改变量仅与系统频率的偏差成正比，式(4)写为变化量形式为：

ΔPWT=-KWTΔf

(6)

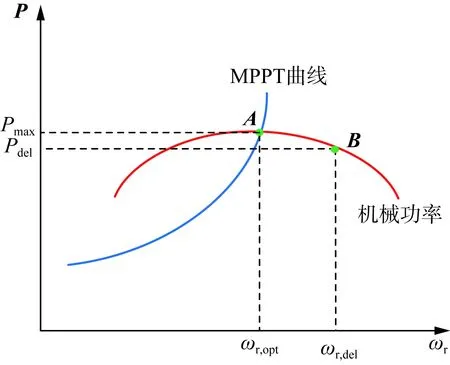
图3 风机机械功率与MPPT功率曲线Fig.3 Curves of MPPT power curve and wind turbine power

联立式(1)、(2)和(6)得到系统的频率响应模型为：

(7)

其中

(8)

对式(7)进行反拉普拉斯变换可以得到频率响应的时域表达式：

(9)

其中

(10)

根据式(9)可以得到频率最低点的表达式：

(11)

式中：Δfnadir为频率最低点所对应的频率偏移量；tnadir为频率最低点所对应的时间。

计算频率最低点对下垂系数KWT的灵敏度：

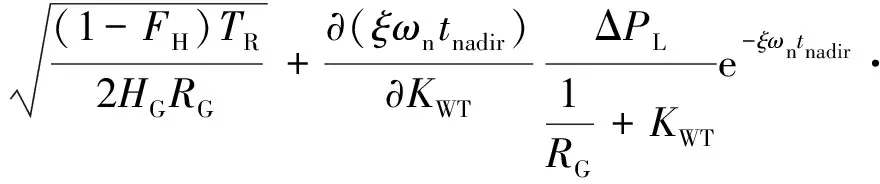
(12)

代入系统参数的典型值则计算出式(12)中的灵敏度为正值，因此增大控制器参数可以提升系统频率的最低点。从式(11)可以得到进入稳态后系统频率偏移为：

(13)

式(13)说明减载方式下风机的备用容量可以参与到系统的一次调频中。

3 MPPT下风机参与调频的系统频率响应模型

3.1 频率响应模型推导

MPPT运行的风机采用频率下垂控制时的输出功率为：

(14)

式中：C为由风机自身参数所决定的MPPT功率常数；wr为风机转速。由于频率支撑过程中风机转速变化范围较小，可对式(14)线性化：

(15)

式中wr0为初始转速，考虑风机转子运动方程：

(16)

式中：HW为风轮机与永磁同步发电机的惯性时间常数之和；Pwind为风机的机械功率。对风机运动方程线性化：

2HWωr0sΔωr=ΔPwind-ΔPWT

(17)

联立式(15)与式(17)得到

(18)

这里风机的机械功率变化可以看作0，原因有两个方面：一是对于频率响应研究的时间尺度内风速可以看作定值；二是风功率曲线在最优转速附近非常平缓，同时风机调频过程中转速只在最优转速附近小范围变化。式(18)表明调频过程中系统频率变化与风机转速变化间存在耦合关系。联立式(15)与(18)得到：

(19)

从式(19)可以看出，在MPPT下风机的调频附加功率与系统频率相互耦合，这是因为系统频率与风机转速相互耦合，同时MPPT的功率参考值随着风机转速的变化而不断变化。因此尽管采用相同的下垂控制器，但是在MPPT下的调频附加功率无法达到与减载方式下相同的值。将式(19)代入式(1)，可以得到MPPT下的系统频率响应模型：

(20)

其中

(21)

对式(20)运用终值定理可以得到系统进入稳态后的频率偏移为：

Δfsteady=-ΔPL·RG

(22)

对比式(13)与(22)可以看出，运行在MPPT的风机无法参与系统的一次调频。

3.2 模型降阶方法

从式(20)可以看出系统的频率响应为三阶，难以直接通过反拉普拉斯变换的方法计算出频率最低点。而通过计算可以得到如图4所示的频率响应模型的传递函数的极点分布，其中包含一个离虚轴较远的负实极点p1和一对共轭极点p2、p3，可以看出各极点之间满足式(23)。

|p1|>5|Re(p2)|=5|Re(p3)|

(23)

故负实极点为传递函数的一个非主导极点，可以采用去掉传递函数展开式中分母为s+p1的项的方法进行降阶。

非主导极点数值随调频控制器下垂系数的变化如图5所示，经拟合可以得到非主导极点的值与下垂系数KWT近似呈一次函数关系：

-p1=-1.05-0.131KWT

(24)

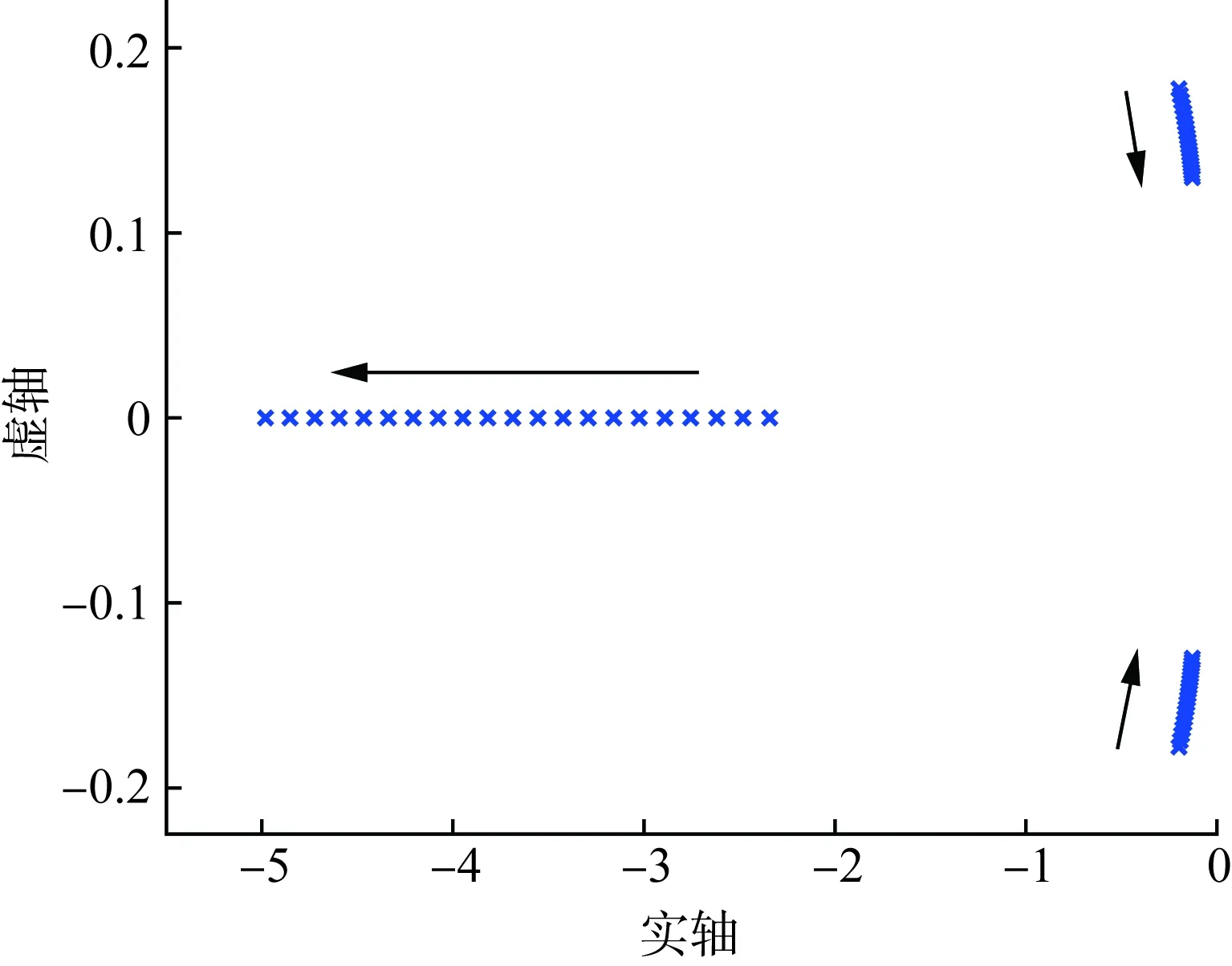
图4 三阶传递函数极点分布Fig.4 Poles positions of the three order transfer function

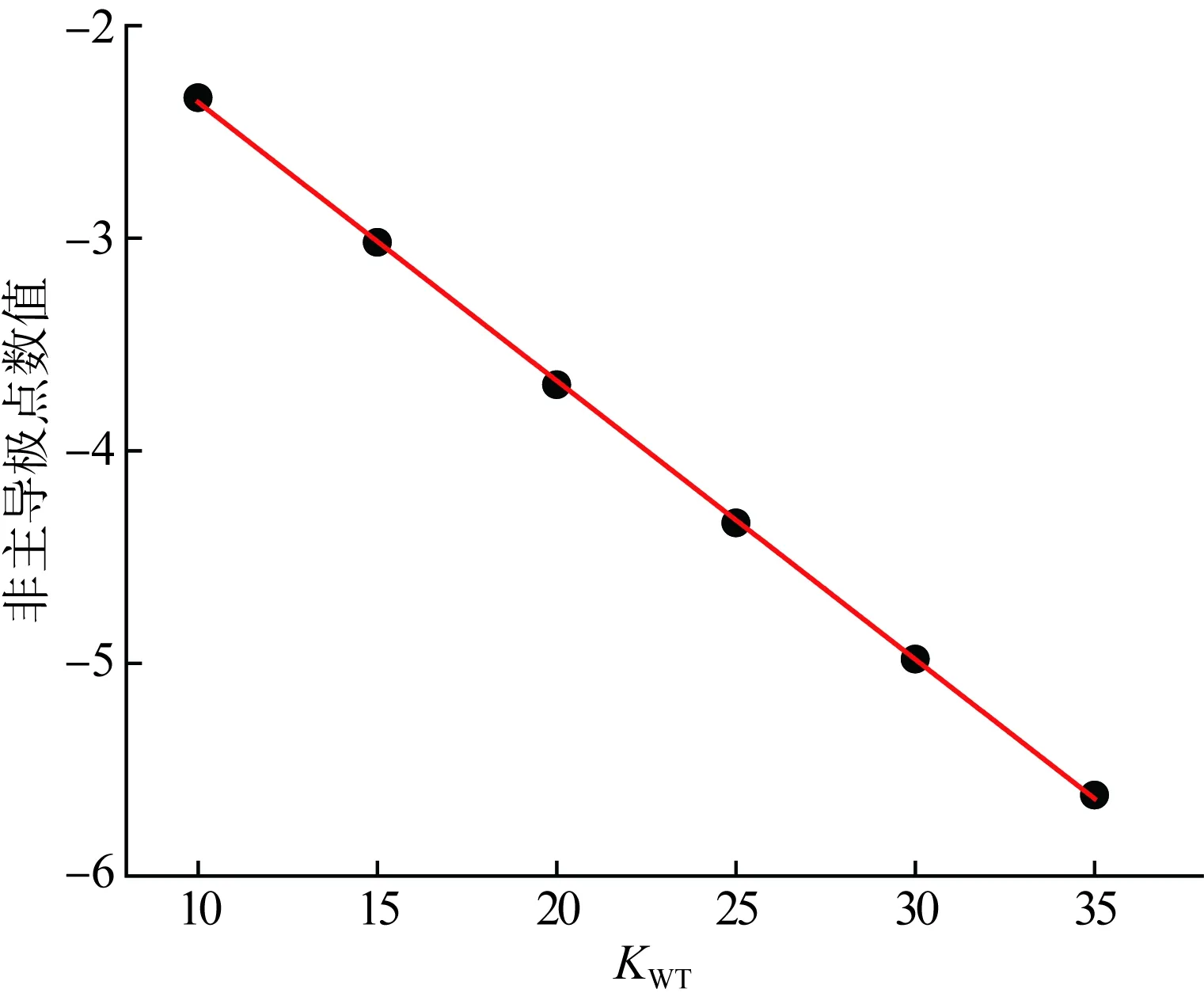
图5 非主导极点数值拟合曲线Fig.5 Fitting curve of the values of the non-dominant poles

那么式(20)可以写为：

(25)

其中

(26)

将式(25)中含p1的项去掉可以得到：

(27)

其中

(28)

采用与减载方式类似的计算方法得到MPPT下频率最低点为：

(29)

其中

(30)

结合式(26)与式(29)可知，MPPT下系统的频率最低点是频率控制器下垂系数及风机初始转速的函数。求频率最低点对下垂系数与初始转速的灵敏度：

(31)

(32)

如图6所示，频率最低点对控制器下垂增益的灵敏度为正，说明增大下垂增益可以提升频率响应。但此灵敏度随下垂增益增大而逐渐下降，尤其在MPPT下控制器下垂系数达到40后灵敏度数值已降至0.001以下，因此当控制器系数较大时增大下垂系数对系统频率响应的提升作用有限。同时，在调频的过程中风机转速下降的大小与控制器的下垂系数紧密相关；若下垂系数过大，在低风速情况下风机可能会因释放过多动能而出现停机的情况，而下垂系数过小则无法充分利用风机的调频能力，因此综合考虑风机调频效果与稳定运行两方面，控制器参数设置在10～40的范围内较为合理。

除了控制器下垂系数，初始转子转速也会影响频率最低点。如图7所示，频率最低点对于初始转速的灵敏度数值为负，说明更高初始转速(意味着更高风速)的情况下频率最低点会更低，即初始转速升高对于频率控制器的调频效果具有一定的削弱作用。

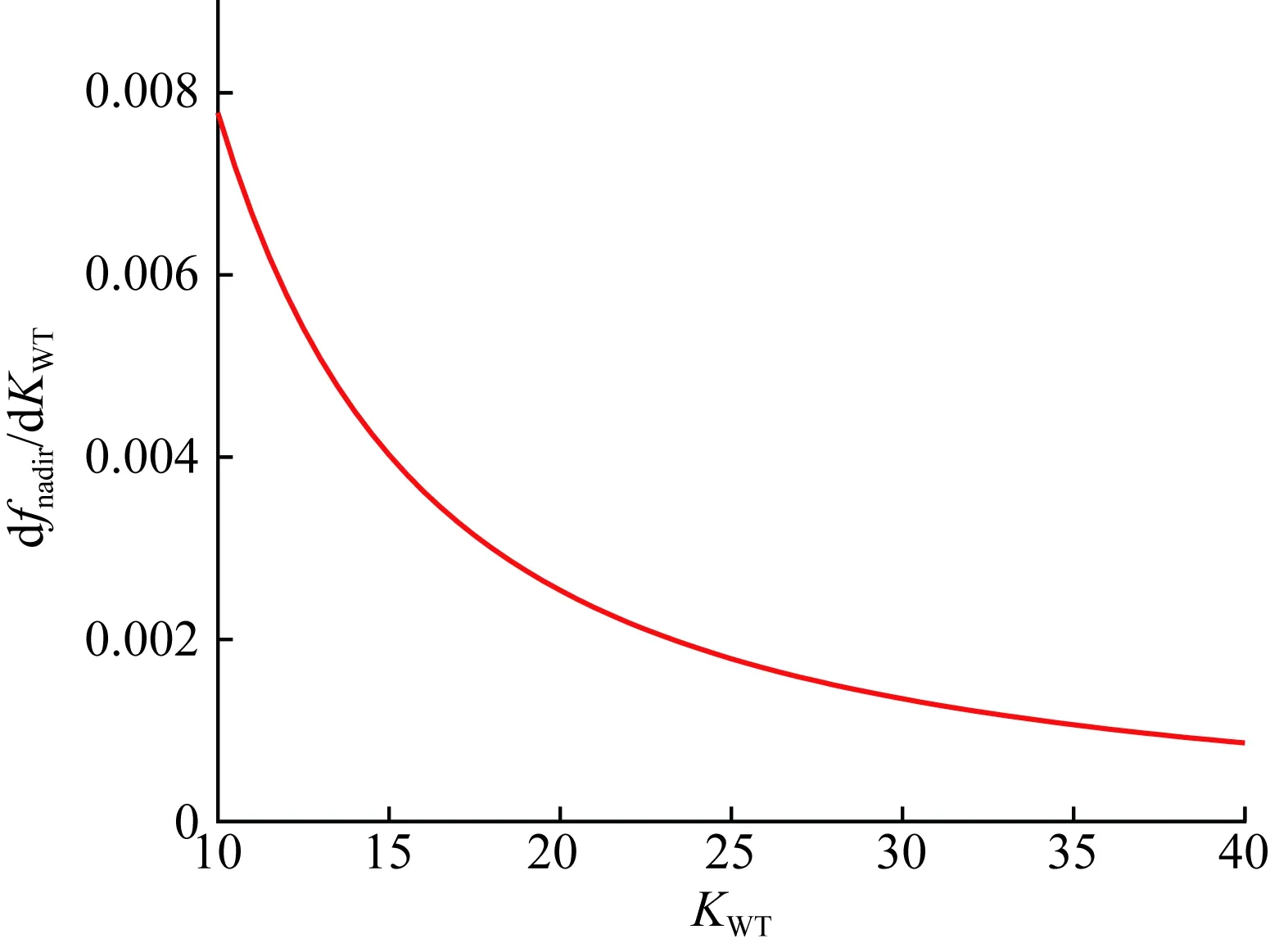
图6 频率最低点对控制器下垂系数的灵敏度Fig.6 Sensitivity of frequency nadirs against the controller droop parameter

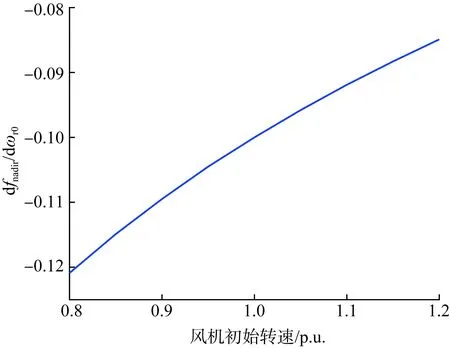
图7 频率最低点对初始转速的灵敏度Fig.7 Sensitivity of frequency nadirs against with respect to WT initial speed

4 算例分析

采用图1所示系统进行仿真，系统已折算到标幺制下，其中总负荷为2.0 p.u.，在5秒时负荷突增0.1 p.u.，同步机采用经典模型并忽略换流器控制的动态过程。为说明调频控制器参数与风机初始转速对系统频率响应的影响，对比了不同下垂系数及初始转速条件下的系统频率响应，同时通过对比每种条件下根据降阶模型所计算出的频率最低点与实际模型的频率最低点，验证了所提出的模型降阶方法的准确性。仿真系统中各参数取值如表1所示。

4.1 算例1：下垂系数10，初始转速1.0 p.u.

当风机不参与频率支撑时，系统的频率响应与传统同步机系统一致，此时频率最低点为49.52 Hz。图8(a)对比了不同风机调频方式与不同模型下的系统频率响应，在全阶模型中，同步机采用的E′恒定的经典模型，同时考虑换流器控制的动态过程。

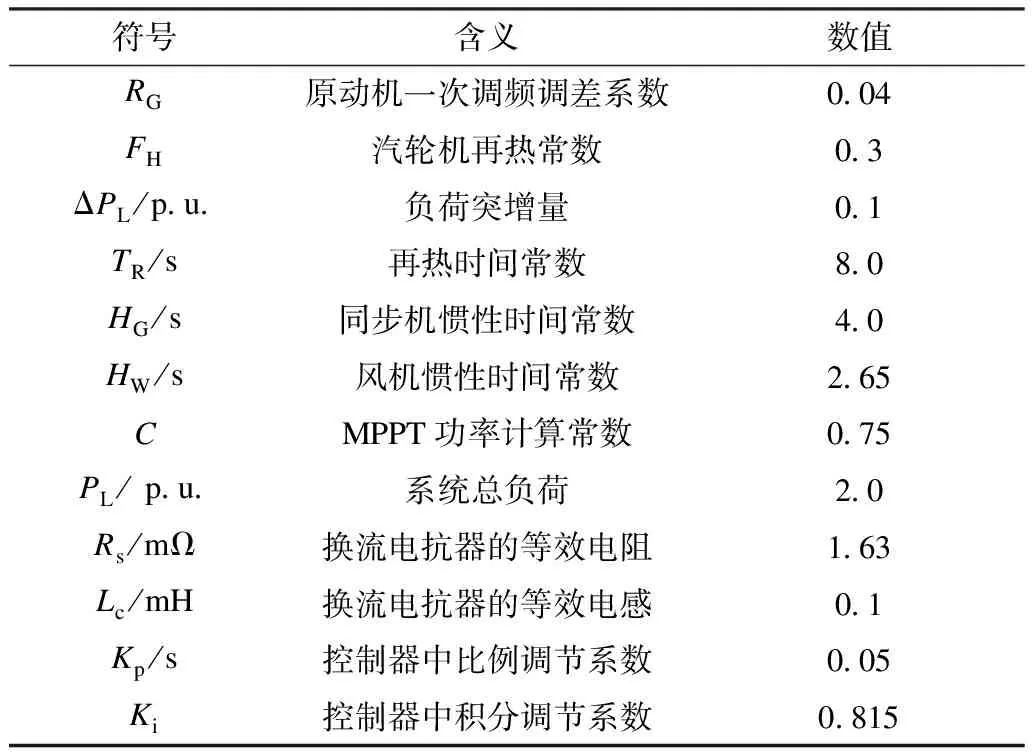
表1 仿真系统参数Tab.1 Simulation system parameters

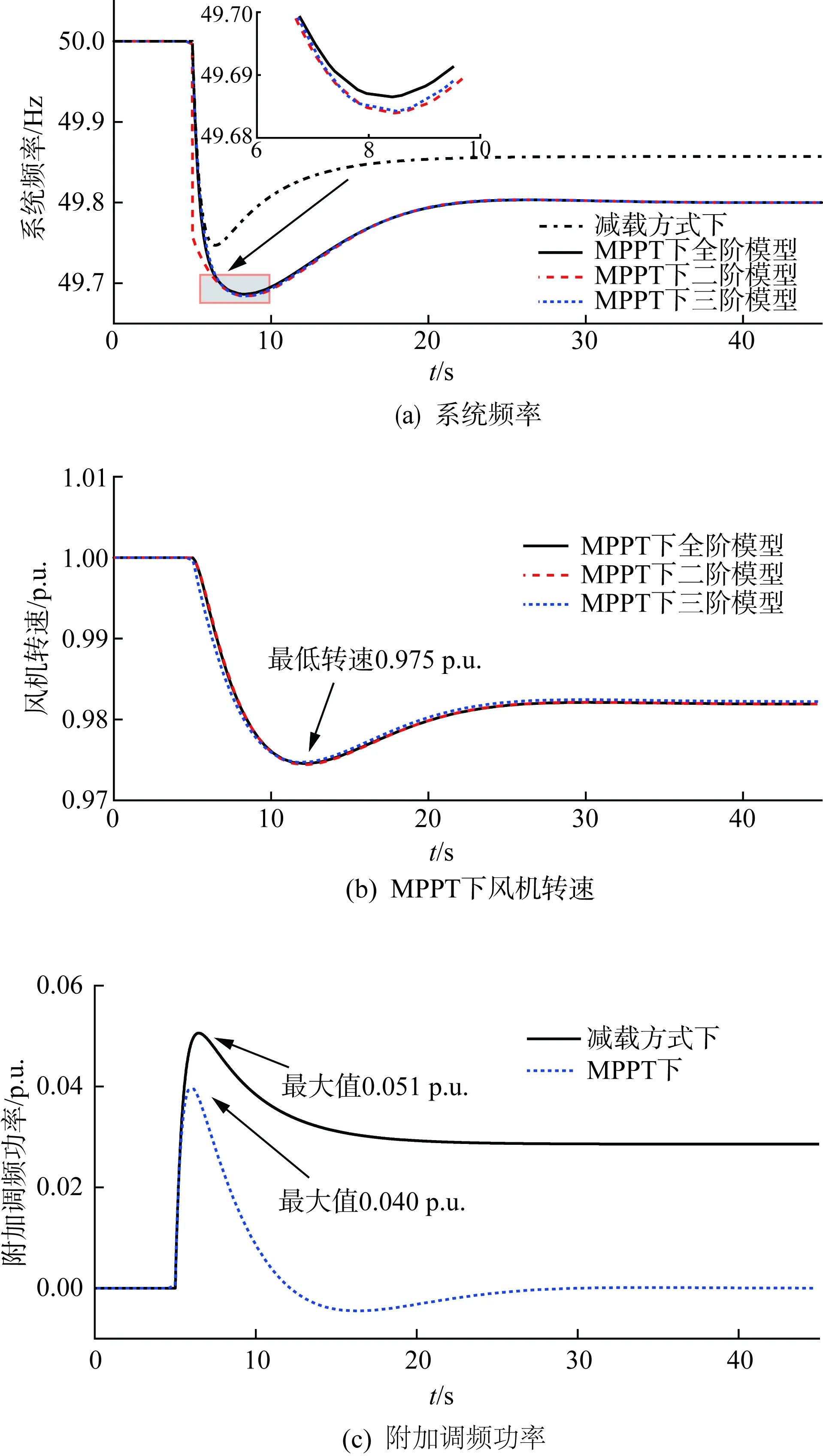
图8 KWT=10, ωr0=1.0下仿真结果Fig.8 Simulation results when KWT=10, ωr0=1.0

从图8(a)可以看出，同步机采用经典模型并忽略换流器控制动态的三阶模型与全阶模型得到的频率响应较为接近，频率最低点的差距为0.002 Hz左右，因此其余算例中均采用二阶模型与三阶模型的对比来验证所提出的模型降阶方法的准确性。

相较于风机不参与调频，运行于MPPT的风机参与调频后频率最低点可以提升至49.68 Hz，但此频率最低点低于减载方式下的49.75 Hz，验证了MPPT对于下垂控制器的调频效果具有一定的削弱作用，原因在于风机在调频过程中，MPPT的功率参考值随着转子转速的下降而下降，因此实际上MPPT减小了用于提供频率支撑的附加功率。

从图8(b)中可以看出在频率支撑过程中风机转速最低降至0.975 p.u.。图8(c)是在减载与MPPT两种方式下风机所输出的附加调频功率，在发生频率扰动后风机在短时间内快速输出附加调频功率，对进行系统频率支撑。在MPPT下附加调频功率的最大值小于减载方式下，分别为0.040 p.u.与0.051 p.u.。由于MPPT功率参考值随转速下降而减小，在MPPT下附加调频功率达到最大值后迅速下降，在11 s左右已降至负值，即此时风机输出功率小于风机参与调频前，在进入稳态后风机的调频附加功率为0，验证了风机运行于MPPT时不具备一次调频能力这一结论。

4.2 算例2：下垂系数20，初始转速1.0 p.u.

算例2与算例1相比采用了更大的控制器下垂系数，如图9(a)所示，此条件下的频率最低点高于算例1中的最低点，减载方式与MPPT下的频率最低点分别达到了49.83 Hz与49.73 Hz，验证了增大控制器下垂系数对于系统频率响应具有较明显的提升作用，这是因为采用更大下垂系数时风机输出更大的附加调频功率。如图9(c)所示，本算例中风机在减载与MPPT两种方式下输出的附加调频功率均大于算例1。

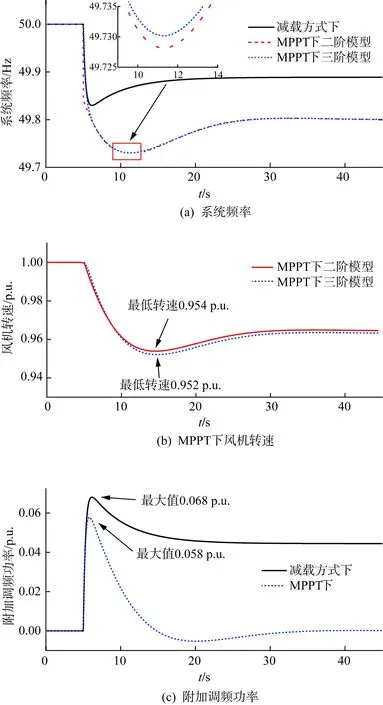
图9 KWT=20, ωr0=1.0下仿真结果Fig.9 Simulation results when KWT=20, ωr0=1.0

对比图8(b)与图9(b)可以看出，采用更大的控制器下垂系数时，风机在频率支撑过程中转速下降更多，最低转速为0.952 p.u.。由降阶模型得到的最低转速与全阶模型结果有0.002 p.u.的差距，这是因为运行于MPPT的风机采用频率下垂控制时风机转速与系统频率相互耦合，两种模型下系统频率的误差导致了转速的误差。

4.3 算例3：下垂系数20，初始转速0.8 p.u.

本算例设置与算例2不同的初始转速，以验证MPPT下系统频率响应与初始转速的关系。仿真结果如图10所示。

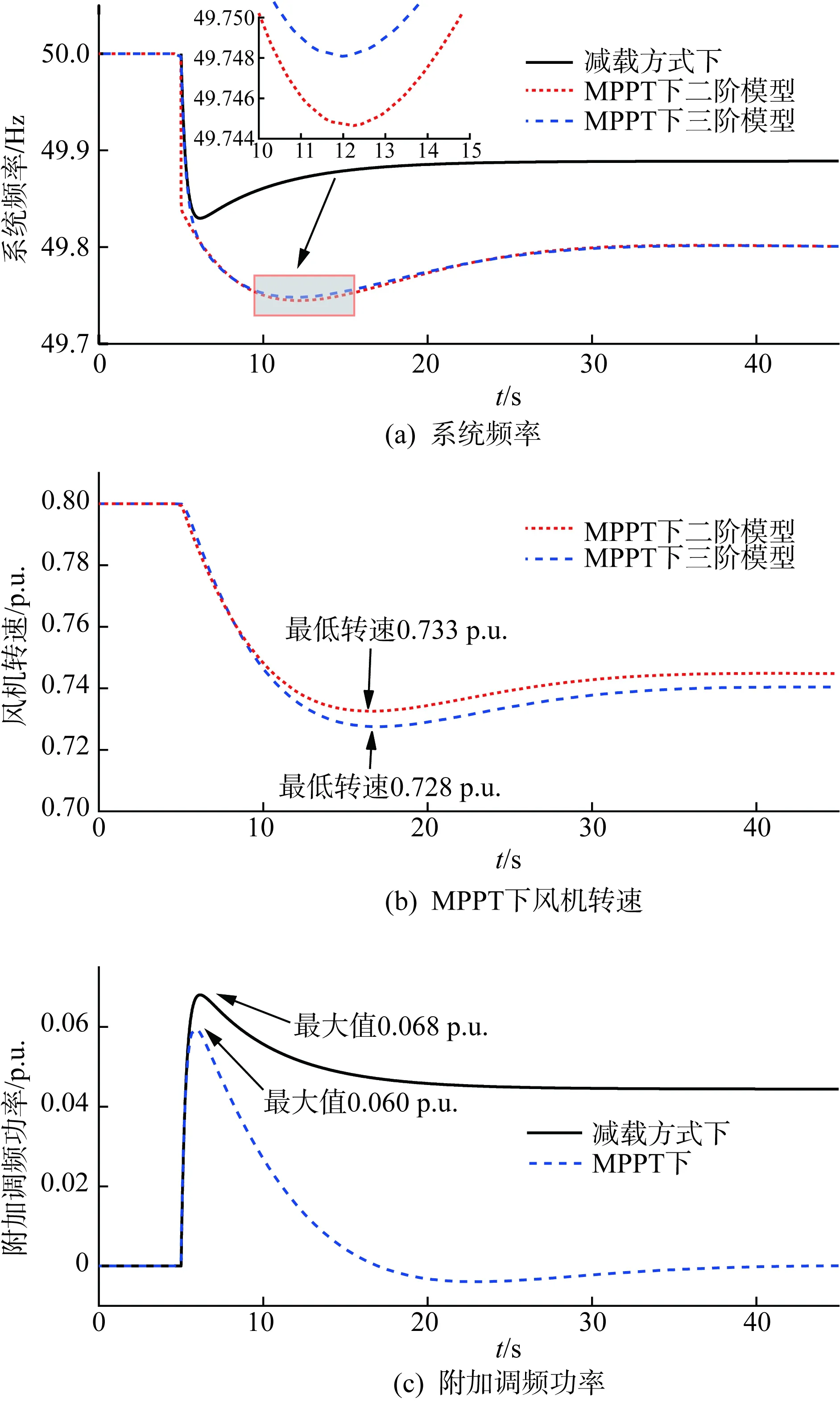
图10 KWT=20, ωr0=0.8下仿真结果Fig.10 Simulation results when KWT=20, ωr0=0.8

从图10(a)可以看出，MPPT下的频率最低点为49.75 Hz，比算例2高出0.02 Hz，验证了初始转速升高系统频率最低点会随之下降的结论。如图10(b)所示，全阶模型与降阶模型计算出的最低转速分别为0.733 p.u.与0.728 p.u.。图10(c)与图9(c)对比可以看出，在MPPT下算例3的调频附加功率要小于算例2，即初始转速升高将造成下垂控制器调频作用的下降。

其余参数下的仿真结果如表2所示，从表2可以看出在各参数下降阶模型与全阶模型的仿真结果都较为接近。在同一下垂系数下，MPPT下的频率最低点低于减载方式下，说明了MPPT会削弱频率下垂控制器的作用，同时频率最低点随着初始转速的升高而降低，说明在更高的风速下这种削弱作用会更加明显。

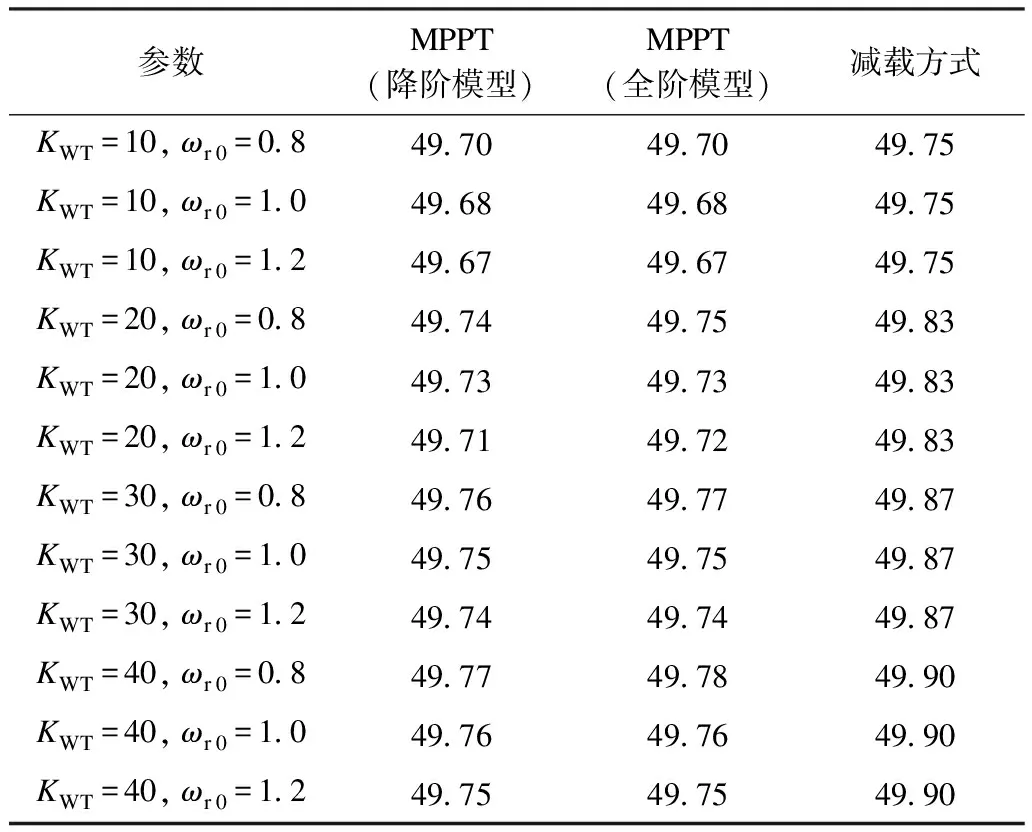
表2 不同风机参数下频率最低点 Tab.2 Frequency nadirs under different WT parametersHz

5 结语

本文推导了风机分别运行在减载以及MPPT两种方式时参与调频的系统频率响应模型，选取频率最低点作为系统频率响应的主要评价指标并给出了两种方式下频率最低点的解析表达式。在减载方式下，系统的频率最低点可以直接通过反拉普拉斯变换计算，但在MPPT下系统频率响应模型阶数较高，难以直接计算频率最低点，因此本文提出了一种模型降阶方法并基于降阶模型计算出MPPT下的系统频率最低点。通过两种方式下频率最低点的对比可以得出MPPT会削弱风机频率控制器的作用。本文进一步计算了MPPT下频率最低点对频率控制器参数与风机初始转速的灵敏度，灵敏度计算的结果从定量角度说明增大控制器参数能够提升频率最低点，但此提升作用会随着控制器参数的增大而下降。同时，频率下垂控制器的作用还会受初始风速的影响，初始风速升高会造成控制器作用的下降。此外，因存在频率控制器启动阈值以及风机输出功率上限，在系统发生轻微或严重频率波动时，控制器可能存在控制死区，但本文重点讨论在下垂控制器限幅内的频率最低点解析计算，控制器死区对系统频率稳定性的影响将在后续工作中研究。