考虑不同故障穿越模式的双馈风电场短路电流计算等值建模
2022-12-01令狐桐雯韩民晓霍启迪唐晓俊
令狐桐雯,韩民晓,霍启迪,唐晓俊
(1. 华北电力大学电气与电子工程学院,北京102206;2. 电网安全与节能国家重点实验室(中国电力科学研究院有限公司),北京100192)
0 引言
近年来,风电、光伏等可再生电源迅速发展,构成了具有双高特点的新一代电力系统[1]。变速恒频的双馈异步风机(doubly-fed induction generator,DFIG)以其卓越的控制特性和较高的风能转换效率,已经成为风电场的主流机型[2]。风力发电与传统能源相比,其故障分析方式存在根本不同[3 - 4],且其复杂性导致含大型风电场的电力系统建模难度大大增加[5]。随着大规模风电场集中接入电网,有必要针对风电并网故障后输出的短路电流进行等值建模。
现有针对DFIG的故障分析集中于单机并网系统。一般认为,双馈风机短路后的暂态行为与机端电压跌落程度、采用的低电压穿越(low voltage ride through, LVRT)策略、故障前稳态功率等因素密切相关[6 - 11]。
目前针对风电场故障暂态等值主要在分群指标和聚类方法上有不同的选择。指标的选取通常分为两类,一类为风电机组非故障扰动时的运行特征数据,多采用风速、转速、机组类型、状态变量矩阵或控制参数等进行机群划分。文献[12]以故障前的转速作为故障下的分群指标,采用K-means算法进行分群。文献[13]以机组的状态变量矩阵为分群指标,包括13个运行特征数据,其数据采样过程较为繁琐。文献[14]以风速、转速、桨距角和输出功率作为分群指标,采用密度聚类Dpeak算法对风电场进行聚类。此类分群依据均未考虑外界故障影响,当故障程度差异较大时难以保证较高的等值精度。
第二类分群指标为故障后的动态特征数据,不涉及风机具体模型参数,主要有短路电流轨迹、转子转速曲线轨迹、机端电压跌落轨迹等。文献[15]以DFIG输出短路电流包络线轨迹的方向、转角、速度和位置相似度为评价指标,采用层次聚类进行暂态同调机群的划分。文献[16]以转子暂态转速轨迹为分群指标,提出基于凝聚层次聚类的分群方法。文献[17]以并网点暂态电压受扰轨迹为分群指标,利用层次树结构展示各风电场群亲疏关系,但在同一风电场内部,仅采用暂态电压单一指标无法有效分群。文献[18]采用Crowbar状态改进识别结果和输入风速作为分群指标,建立以判断Crowbar保护是否动作为目的的风电场等值模型。
针对DFIG故障后不同LVRT模式下电流分量、衰减时间常数以及主要影响因素不同的特点,在分群依据上进行综合考虑,提出一种风电场故障暂态等值建模方法。以描述故障扰动的电压跌落和表征运行点高低的转子转速为分群指标,考虑指标在故障瞬间和全过程的作用,采用凝聚式层次聚类法分别在故障过渡和稳态阶段进行分群,以输出短路电流一致为原则进行参数等值,得到在故障全阶段均可准确描述输出电流特性的等值模型。
1 双馈风机单机短路电流特性
1.1 双馈风机数学模型
通常DFIG定子侧变流器(grid side converter, GSC)采用定子电压定向控制,转子侧变流器(rotor side converter, RSC)采用定子磁链定向控制,通过调节d、q轴电流,实现风机有功、无功功率的解耦控制。
定子三相静止坐标系中以空间矢量形式表示的DFIG电压和磁链方程为:
(1)
(2)
ψs=Lsis+Lmir
(3)
ψr=Lrir+Lmis
(4)
式中:us、ur分别为定子、转子电压;is、ir分别为定子、转子电流;ψs、ψr分别为定、转子磁链空间矢量;Rs、Rr分别为定子、转子电阻;Ls、Lr分别为定子等效电感;Lm为励磁电感;ωr为转子角速度。
1.2 低电压穿越控制策略
随着风电场应用愈加广泛,风电场普遍具备了LVRT能力。我国标准规定[19],短路故障使电压跌落在区间[0.2 p.u., 0.9 p.u.]时,风电场应为电网提供无功功率支撑。若故障程度严重,转子电流超过额定电流的2倍[20],为防止风机设备在故障时损坏,应迅速封锁RSC,投入撬棒保护;待经过一定时间,过剩能量在撬棒电阻上消耗后,撬棒保护退出,重新恢复RSC励磁控制。图1为DFIG故障检测及控制结构。
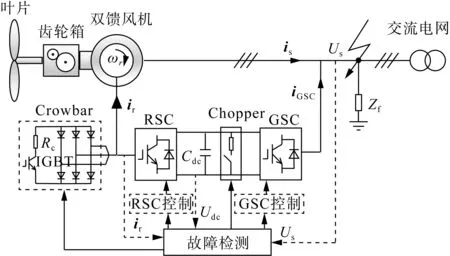
图1 DFIG故障检测及控制结构Fig.1 DFIG fault detection and control structure
1.3 DFIG输出短路电流特性
双馈风机输出的电流包括两部分:定子绕组电流is和网侧变流器电流iGSC。鉴于GSC容量仅为额定容量的30%,其交流侧电流对短路电流的贡献十分有限,因此本研究主要针对定子绕组电流is展开。
由式(3)可得定子电流为:
(5)
式中定子电流由定子磁链和转子电流共同决定。
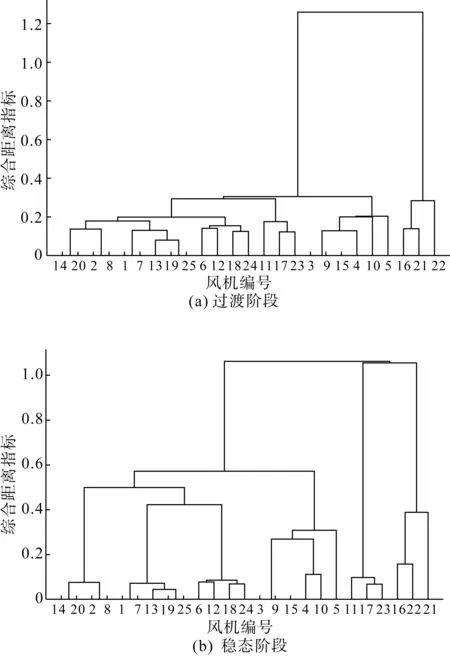
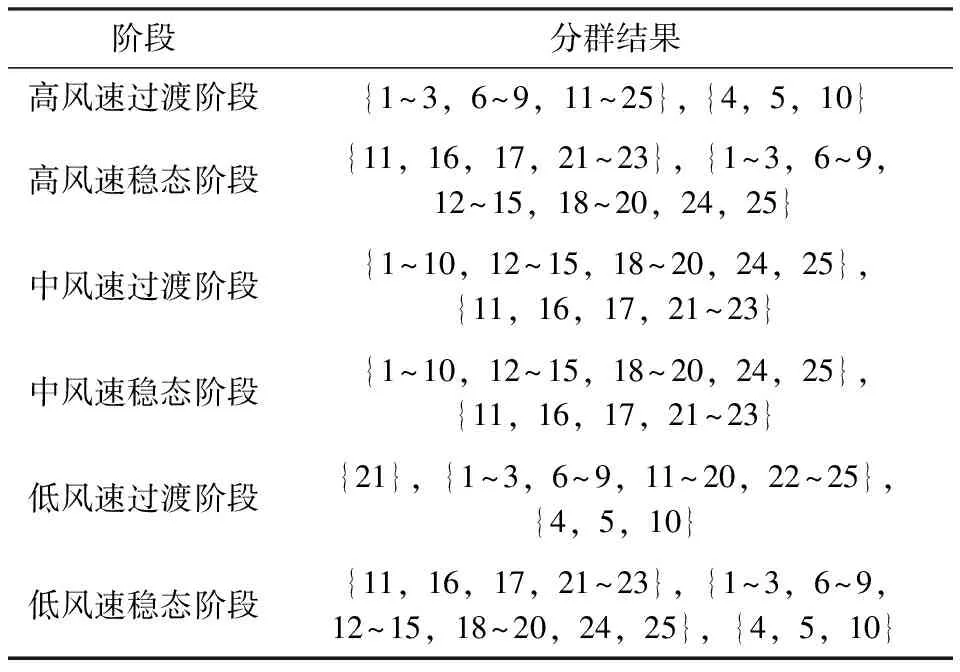
假设DFIG稳态机端电压幅值为Us,t0时刻发生三相短路故障,电压幅值跌落至kUs,0 (6) (7) 式中:usf为故障定子电压空间矢量;ωs为同步角速度。 由式(1)得到定子磁链表达式为: (8) 由于磁链守恒,电压跌落后定子磁链将产生暂态直流分量,该分量与故障发生时刻和电压跌落程度有关,若忽略转子感应电流对定子磁链的影响,可得到定子磁链: (9) 式中τs为定子时间常数,τs=Rs/Ls。 将式(4)—(5)代入式(2),得到转子电流的一阶微分方程为: (10) 式中:σ为漏磁系数,σ=1-(Lm2/LsLr)。 1.3.1 考虑撬棒保护动作的短路电流特性 撬棒保护以检测转子侧过电流和直流侧过电压为触发条件,由于从故障检测到撬棒保护投入仅需要几个毫秒,可以忽略检测过程的影响,认为在短路瞬间,转子绕组就与撬棒电阻Rc短接。撬棒保护投入后,转子侧等效电阻增大至Rrc。 Rrc=Rc+Rr (11) 短路故障撬棒保护投入后,转子电压ur瞬间跌落为0,有: (12) 式中:αrc、βrc、γrc均为Crowbar保护动作后的转子电流解析式系数。转子电流空间矢量以转差角频率ωs-r旋转,假设其在t0时刻的初值为ir0: ir0=Ir0ejωs-rt0 (13) 式中Ir0为正常运行时的转子电流幅值。求解关于转子电流的一阶微分方程,得到故障后撬棒保护投入时的转子电流表达式。 (14) 式中:上标r表示在转子旋转坐标系下;τrc为转子等效时间常数,τrc=Rrc/σLr,系数见附录A。 将式(14)代入式(5),可得故障后撬棒保护投入时的定子电流表达式: isc=αscejωst+βscejωrte-τrct+γsce-τst (15) 式中:αsc、βsc、γsc均为Crowbar保护动作后的定子电流解析式系数。定子电流包含稳态工频分量、以转子时间常数τrc衰减的转速频率分量和以定子时间常数τs衰减的暂态直流分量。 其中稳态工频分量的幅值与s-1和电压跌落程度成正比,由于转差率s=(ωs-ωr)/ωs,系数αrc中的s-1=-ωr/ωs,相当于转子转速标幺值ωr。撬棒保护投入时定转子短路电流分量及其影响因素如表1所示,影响因素仅考虑外部状态参数,未考虑固有参数的影响。 表1 撬棒保护动作下定转子电流分量及其影响因素Tab.1 Components and influencing factors of stator and rotor current under crowbar protection control 1.3.2 考虑RSC无功补偿控制下的短路电流特性 若电网故障后转子过电流不至于开启撬棒保护,则RSC进入无功补偿模式:功率外环闭锁,直接计算转子电流参考值,经过内环控制,输出转子电压指令值urref,假设电流内环的控制带宽足够大,RSC交流电压ur能很好跟踪指令值urref,转子电压空间矢量方程可表示为: (16) 其中转子电流参考值为: (17) 式中:irfdref、irfqref分别为故障时RSC无功、有功电流指令值;irqref0为RSC功率外环给定的有功电流指令值;Irmax为RSC最大允许电流。代入式(10)可得转子电流动态方程为: (18) 式中:a1、a2、a3均为RSC励磁控制时转子电流二阶方程系数;irlref为转子电流指令值;τs为短路后与定子磁链有关的衰减时间常数。 在RSC持续励磁的控制下,转子回路动态过程可被表示成二阶微分方程的形式,求解该微分方程可得到转子电流解析式: (19) isl=αslejωst+βsle-τst+γsl(δ2eδ1t-δ1eδ2t) (20) 式中:αsl、βsl、γsl为RSC励磁控制无功补偿时定子电流解析式系数。定子电流包含稳态工频分量、暂态直流分量和暂态自然分量。其中强制工频分量与发电机参数、机端电压跌落程度和稳态参数有关;暂态直流分量由磁链守恒引起,衰减时间常数与定子电阻有关;暂态自然分量由定子磁链和RSC相互作用产生,衰减时间常数受换流器PI控制参数影响。 表2为RSC励磁控制下定转子的电流分量及其影响因素。 从电网角度看,风电场对外输出的短路电流特性是基于整个电场所表现出来的特性,其内部的详细特性可作为次要矛盾忽略。应采用合理的分群指标、相似性度量方法、聚类方法和等值原则,得到适用于短路电流计算的风电场等值模型。 表2 RSC励磁控制下定转子电流分量及其影响因素Tab.2 Components and influencing factors of stator and rotor current under RSC excitation control 根据第1节的分析,双馈风机单机短路电流包含衰减分量和稳态工频分量,基本由外部输入的故障扰动和风机本身稳态运行点决定。 并网点短路故障造成电压跌落,大型风电场由于集电线路阻抗存在,各台机组与故障点电气距离不同,感受到的电压跌落程度不同,将会触发不同的保护机制:非严重故障下,RSC切换至无功补偿模式;严重故障下则进入撬棒保护模式。短路电流特性在两种模式下不同,因此电压跌落程度具有特征意义。 受到相同电压跌落扰动的风机,由于运行点的不同,也会表现出不同的低电压穿越行为,其短路电流仍存在较大差异,因此运行点高低也具有特征意义。对运行在最大功率跟踪(maximum power point tracking,MPPT)范围的机组,有功功率对输出电流的影响可包含在风速或转子转速中,而转速变化相对风速较为缓慢,且风电场可实时监测风机转速,因此选取转速作为描述风机运行点高低的分群指标。 考虑到数据采样的可行性和风电场等值模型实时仿真的要求,选取的分群指标包括故障实时电压轨迹和故障实时转速轨迹。 若有N台待分群的风电机组,定义元素为综合距离函数λij的N×N维距离矩阵,以衡量风机(i,j)间的相似性,并有λij=λji,λii=0。λij越接近0,表示两台风机的特征指标越接近(相似度越高)。 由于短路电流包含衰减分量和稳态分量,即故障后存在过渡阶段和稳态阶段,两阶段影响因素有差异:过渡阶段受故障瞬间干扰程度和运行点高低影响较大,而稳态阶段受故障后电压幅值和运行状态共同影响。因此将分群指标按作用效果的阶段划分为:故障瞬间电压跌落程度、故障全过程电压轨迹、故障瞬间转速、故障全过程转速轨迹。 2.2.1 故障瞬间电压跌落程度指标 提取机端电压轨迹usi(1 Δusi=|usi(t0)-us0|=1-ki (21) 式中:Δusi为第i台风机故障瞬间机端电压跌落程度;us0为故障前的机端电压;ki为第i台风机故障后机端电压标幺值。选取绝对值距离来描述两台风机故障瞬间电压跌落的相似性,指标定义为: λ1ij=|Δusi-Δusj| (22) 式中:λ1ij为电压绝对值距离,表示第i和第j台风机在故障瞬间电压跌落的不同程度,其值越小表示外界故障的影响程度越接近。 2.2.2 故障全过程电压轨迹指标 “帮助俺脱贫致富,甩掉穷帽子,是天大的好事,俺愿意试试。”郭书凤寻思再三,觉得养兔比较实际,并于当月花费5000元,购买了50只长毛赖兔,政府则通过到户增收的政策及时地给郭书凤家3000元的扶持资金。经过一年多的精心饲养,郭书凤原来的50只兔,发展到了目前的350只。 电压轨迹本质上是一种受扰曲线。选取皮尔森相关系数(Pearson correlation)来描述两台风机电压轨迹的近似程度,假设故障全过程(t0,T)中电压轨迹共有Z个采样点,定义皮尔森相关系数指标r2ij为: (23) λ2ij=1-r2ij (24) 式中:λ2ij为电压轨迹距离,表示第i和第j台风机在故障全过程电压轨迹的相似程度,其值越小表示电压轨迹越接近。 2.2.3 故障瞬间转速指标 提取转速轨迹ωri(1 λ3ij=|ωri-ωrj| (25) 式中λ3ij为转速绝对值距离,反映短路电流初始运行状态的差异程度,其值越小表示两台风机运行点越接近。 2.2.4 故障全过程转速轨迹指标 反应故障全过程风机运行点的高低,即短路电流的故障稳态幅值。同样采用皮尔森相关系数确定故障全过程转速轨迹的相似程度: (26) λ4ij=1-r4ij (27) 绝对值距离用于描述外界故障扰动暂态阶段的相似程度,属于局部描述;由皮尔森相关系数生成的轨迹距离反映了故障全过程动态特性的相似度,是一种全局描述。 2.2.5 指标的归一化处理 为消除距离指标之间量纲不同及值域范围的影响,采用极差法对指标λ1ij和λ3ij进行归一化处理: (28) 式中:λ′ij、λij分别为归一化前、后距离指标;λ′ij_max、λ′ij_min分别为指标数据的最大值和最小值,归一化后的指标范围为[0,1]。 2.2.6 相似度权重确定 大型风电场中风机运行点高低和受到故障扰动程度不尽相同,DFIG控制模式分为3个阶段:阶段1:稳态运行;阶段2:Crowbar保护控制模式;阶段3:RSC无功功率补偿控制模式。部分风机存在阶段2,部分风机直接进入阶段3,如图2所示。 图2 故障后控制模式阶段Fig.2 Control mode stage after the fault 撬棒保护投入时间一般设定为百余毫秒,风机退出撬棒保护后均运行在RSC无功补偿模式。对故障全过程的等值建模可分为两个阶段:故障过渡阶段和稳态阶段。以撬棒保护投入时间作为分界。 从指标对不同阶段特征的描述来看,λ′1ij和λ′3ij对过渡阶段影响较大,而λ2ij和λ4ij对稳态阶段或全过程影响较大。不同指标影响程度在定子电流解析式的系数中有所体现,利用求灵敏度的方式计算特征指标的权重,即当该特征指标稍有变化时,定子电流的变化程度: (29) 式中:w′p为过渡阶段定子电流变化率;p=1、2、3、4,分别对应指标λ1ij~λ4ij的权重;θp为分群指标,包括机端电压Us和转速ωr。对过渡阶段权重的求取采用定子电流式(15),对稳态阶段权重的求取采用式(20)。指标的权重越大,其决定作用越明显,该指标距离小的风机相似度越高。得到基于权重的综合距离指标为: (30) 得到风机间的相互距离λij后,如果λij值较小,说明两风机受扰后其动态行为相近,可视为具有同群特性,否则被划分到不同场群。 聚类分析是在不明确数据分布的情况下,将一个数据集合划分成多个具有各自特征的数据集的过程[21]。本文采用凝聚式层次聚类法(hierarchical agglomerative clustering,HAC[22])对风电场进行分群,采用降维的方式将多维数据之间的联系表示成低维数据。其好处为不用指定簇的具体个数,待聚类完成后,可在任意层次得到指定数目的簇。 HAC算法本质为最优化计算,目标为分群后簇中个体间的距离最小(相似度最大)。步骤如下: 1)提取特征指标,将每个样本当作一簇; 2)定义相似度距离指标,表征每两簇之间特征指标的近似程度; 3)计算任意两簇之间的距离指标λij,形成簇间距离矩阵,找到距离最近的两簇并合并; 4)重复步骤3),直到两簇的距离指标超过阈值,或最终合并为一个簇,终止聚类,得到最终的聚类结果。 额定容量、定转子参数、惯性时间常数等均采用容量加权法进行计算,具体计算见文献[23]。风电场集电线路根据等值机输出短路电流不变的原则进行等值。对于所示的m行n列风电场结构,经过等值后的拓扑结构如图3所示。 图3 风电场集电线路等值拓扑Fig.3 Equivalent topology structure of wind farm collecting line 经过计算[23],等值线路阻抗为: (31) 式中:m为机组并联数量;n为集电线路引出条数,Zeq为等值线路阻抗;Pi为第i台机组的输出功率;Zi为第i台机组的线路阻抗。 风电场等值建模流程图如图4所示。 图4 基于HAC的双馈风电场等值建模流程图Fig.4 Equivalent modeling flow diagram of doubly-fed Wind farm based on HAC 以上海如东某海上风电场为例,验证算法。该风电装机以单机2 MW双馈机组为主,在PSCAD中建立由25台(5×5)风机构成的风电场详细模型,经过机端三绕组变压器35 kV/0.69 kV/0.69 kV(未画出)升压至35 kV并汇集,再经过升压变压器并入电网[24]。风电场集电线路等效阻抗为0.05+j0.12 Ω/km,假设风机间距500 m。Crowbar保护门槛电流为2倍转子额定电流,Crowbar电阻为1.5 Ω,投入时间为0.1 s。拓扑如图5所示,参数如表3所示。 图5 风电场详细模型仿真拓扑结构Fig.5 Topological structure of wind farm simulation 表3 风机仿真参数Tab.3 Wind turbine simulation parameter 令每台风机工作在不同的运行状态,为不失一般性,考虑尾流效应的影响[25],假设自然风速为14 m/s,风向45 °,风机初始风速如表4所示,其中W为风机编号。 针对35 kV母线处三相短路故障进行仿真,故障发生在3 s,电压跌落至约70%。分段聚类得到过渡阶段和稳态阶段的层次树如图6所示。不同类别的风机原始数据点是树的最底层,树的顶层是一个聚类的根节点。分群结果如表5所示。 表4 风机初始风速Tab.4 Initial wind speed of wind farm 图6 HAC聚类树形图Fig.6 HAC clustering tree diagram 表5 分群结果Tab.5 Clustering results 过渡阶段风机分为2簇,其中{16,21,22}为一簇,该簇内的风机均投入撬棒保护,其余始终通过RSC进行LVRT控制的机组为另一簇,分群结果反映了不同风机的实际故障动作特性。撬棒保护动作的风机,其过渡过程的冲击电流较大,但由于撬棒电阻的耗能,直流分量的衰减较快;直接进入RSC控制的风机,直流分量衰减相对较慢。两种故障控制方式下,短路电流过渡过程有较大区别。稳态阶段分为3簇,对应初始风速表中同一风速带下的风机(较大风速、中间风速和较小风速),分群结果反应了不同风机的稳态运行点影响。实际应用中可适当调整簇的数目。 详细模型和两阶段等值模型的短路电流如图7(a)所示。为验证本文所提方法的有效性,加入基于风速加权的单机等值模型和与文献[14]提出的采用稳态数据的分群方法进行对比,并在不同故障程度下多次仿真,结果如图7和表6所示。 图7 故障期间输出A相短路电流Fig.7 A-phase short-circuit current during the fault 表6 等值模型误差评价指标Tab.6 Error evaluation index of equivalent model 平均误差δmean为等值模型与详细模型所有采样点平均值的差别,峰值误差δpeak为等值模型与详细模型故障波形峰值的差别,如式(32)—(33)所示。 (32) (33) 式中:Is(n)和Iseq(n)分别为详细模型和等值模型电流采样值;Z为采样点数。 由图7(a)可以看出,在过渡阶段使用稳态权重进行划分使得结果偏差较大,反之同样,因此按照不同阶段分群,可以避免非主要影响因素干扰下的偏移,得到的等值模型在暂态和稳态全阶段均具有较高的等值精度。由图7(b)和表6可以看出,基于风速的单机等值未考虑不同故障穿越模式,将整个风电场等值为一台风机,在Crowbar投入阶段存在不可忽视的偏差;而文献[14]方法未将故障影响纳入分群依据,因而在大范围电压跌落下不完全适用。相较而言,本文方法在故障的暂稳态阶段均可准确描述短路电流特性,更能反映实际风电场动态行为。 为进一步说明本方法在不同风速下的适应性,对电压跌落为30%,自然风速为14 m/s、11 m/s和8 m/s 3个场景进行等值(风向和尾流因子同上),分群结果如表7所示。 表7 不同风速下的分群结果Tab.7 Clustering results at different wind speeds 将本文方法与文献[14]方法及单机等值方法进行对比,不同等值方法误差评价指标如表8所示。 分析表7和表8可知,运行点高低影响分群结果和误差水平。各类场景下,单机等值均有较大误差;而本文方法等值准确性要优于文献[14]方法,尤其表现在过渡阶段。本文方法的最大平均误差为0.48%,最大峰值误差为3.64%。相比之下,本文方法在各个风速场景下具有更好的适应性。 表8 不同等值方法误差评价指标Tab.8 Error evaluation index of different equivalent methods 风电场短路电流分析是进行故障控制与无功补偿的基础。本文提出一种输出短路电流一致性的双馈风电场等值建模方法,并通过详细模型与等值模型的仿真对比验证方法的有效性。 该方法以表征外界故障的电压跌落和表征风机自身运行点的转速作为分群判据,分群指标的获取较易。考虑不同低电压穿越模式和不同阶段下短路电流主要决定因素不同,以撬棒保护整定时间为分界,分阶段对风电场进行层次聚类,按照输出短路电流不变的原则对机组集电参数进行等值。等值模型在故障全阶段均可较好地模拟输出短路电流,可满足新能源电力系统电磁暂态分析的需求,具有工程实用价值。


2 分群指标选择及距离函数计算

2.1 分群指标
2.2 综合距离函数


3 基于HAC的风电场分群等值
3.1 基于HAC的风电场聚类模型建立
3.2 参数等值

4 算例分析
4.1 风电场仿真等值模型







5 结语
