全球涌浪池分布及年际变化分析❋
2022-12-01李松霖于华明王春晓
李松霖, 于华明,2❋❋, 王春晓
(1. 中国海洋大学海洋与大气学院, 山东 青岛 266100; 2. 中国海洋大学三亚海洋研究院, 海南 三亚 572025)
海浪是海表普遍存在的波动现象,根据形成原因分为风浪、涌浪和混合浪。相比于风浪,涌浪拥有更快的传播速度,更长的周期、波长、传播距离[1]。当较快移动的涌浪到达风速较弱区域时会对风产生影响,这一现象由Harris[2]在水槽实验中首次证实,命名为“波驱动风(Wave-driven wind)”。大洋观测证实了微风中快速运动的涌浪会使海表面向大气直接输运动量[3-4]。随着涌浪在海-气相互作用中重要作用被揭示与证实,针对涌浪的研究也相继展开。
Chen等[5]基于充分成长的风浪波高经验公式和概率统计,提出了基于风速和有效波高判断涌浪事件的方法,Jiang等[6]在此基础上借助Jason-1卫星高度计观测的海浪有效波高,对涌浪的全球分布进行了计算,指出大洋季节性涌浪池的存在。但受限于单一卫星观测资料时空连续性差的缺点,该研究仅生成了全球1(°)×1(°)分辨率多年季节平均的涌浪数据,并未对涌浪分布的年际变化进行分析。
相比观测数据存在时空连续性差的问题,海浪再分析数据兼备了模式数据的连续性和观测数据的准确性,成为分析气象和海洋物理过程必不可少的重要支撑。邓增安等[7]基于欧洲中期数值预报中心(European Centre for Medium-Range Weather Forecasts,ECMWF)提供的ERA-Interim海浪再分析资料,使用Chen等[5]提出的涌浪计算方法,确定了东太平洋涌浪池的存在,分析了涌浪池波浪产生的水体体积输运,指出涌浪的体积输运会对大洋环流产生潜在的影响。Anoop等[8]使用ERA-Interim海浪再分析资料,采用Chen等[5]提出的涌浪算法,对北印度洋的涌浪波候特征进行了分析,指出季风前后北印度洋存在南半球传来的能量巨大的涌浪。
前人对涌浪信息的提取采用经验公式与概率统计相结合的方法,主要是限于所用的海浪再分析数据仅包含有效波高而不包含海浪谱信息而采取的无奈之举。虽然目前ECMWF发布的第五代再分析产品ERA5包含了涌浪信息,但其空间分辨率仅为0.5(°)×0.5(°),在岛礁较多的区域适用性较差。
本文基于第三代海浪模式WaveWatch III v6.07,同化11颗卫星高度计有效波高数据[9],生成包含海浪二维方向谱的30年海浪再分析数据集(Wave Reanalysis Data,WRD)。由于长时间全球再分析数据集占用极大的数据存储空间,数据处理难度较大,目前国内外鲜有全球涌浪分布及年际变化研究,本文基于全球海浪再分析数据产品,对全球涌浪池分布及年际变化开展分析。
1 全球海浪再分析数据产品简介
1.1 全球海浪再分析系统介绍
全球海浪再分析系统[9]基于第三代海浪模式WaveWatchIII v6.07构建,模型基于波能量守恒方程,考虑了线性输入项、风输入项、耗散项、非线性波-波相互作用项、底作用项、深度诱导破碎项、两极海冰作用项等。风场来源为ERA5提供的10 m风场,并融合台风资料进行风场重构[10],海浪同化数据为卫星高度计观测的有效波高,包含ERS-1、ERS-2、Jason-1、Jason-2、Jason-3、T/P、GFO、Envisat、Cryosat-2、SARAL、HY-2A,共计11颗卫星海浪数据,数据同化采用最优插值(Optimal Interpolation,OI)同化方法,海浪再分析系统流程如图 1所示。模型方向谱在角度分量上从0°~350°均匀分为36个离散方向,在频率分量上以1.1为底数指数增长,从0.041~0.65 Hz共分为30个离散频率。模型空间范围80°S—80°N,180°W—180°E,水平分辨率0.1°,时间间隔3 h,时间长度1988—2017年共30年,输出结果包括:有效波高、平均周期、平均波向、二维方向谱、平均波长、平均波速等。本研究所用WRD产品与ERA5产品的详细对比如表 1所示。两类产品所基于的海浪模型均属于谱模式,其中,ERA5海浪产品基于WAM模型,而WRD产品所基于的海浪模型是在WAM模型的基础上发展而来的WaveWatch III海浪模型;在海浪同化方法上,两类产品采用了同样的OI同化方法;在产品水平分辨率上,WRD产品优于ERA5产品,而在时间间隔上,ERA5产品优于WRD产品;与ERA5产品相比,WRD产品包含的海浪方向谱数据能够提供更多的海浪信息,也能为后续的海浪研究工作提供重要数据支撑。
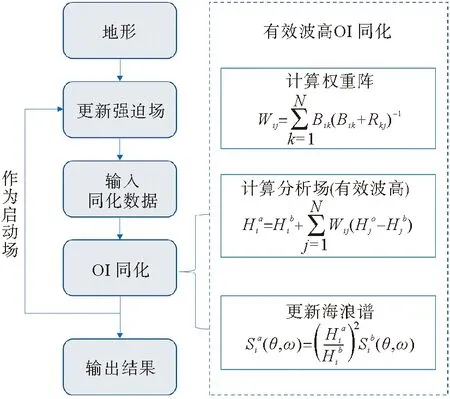
图1 海浪数据同化流程
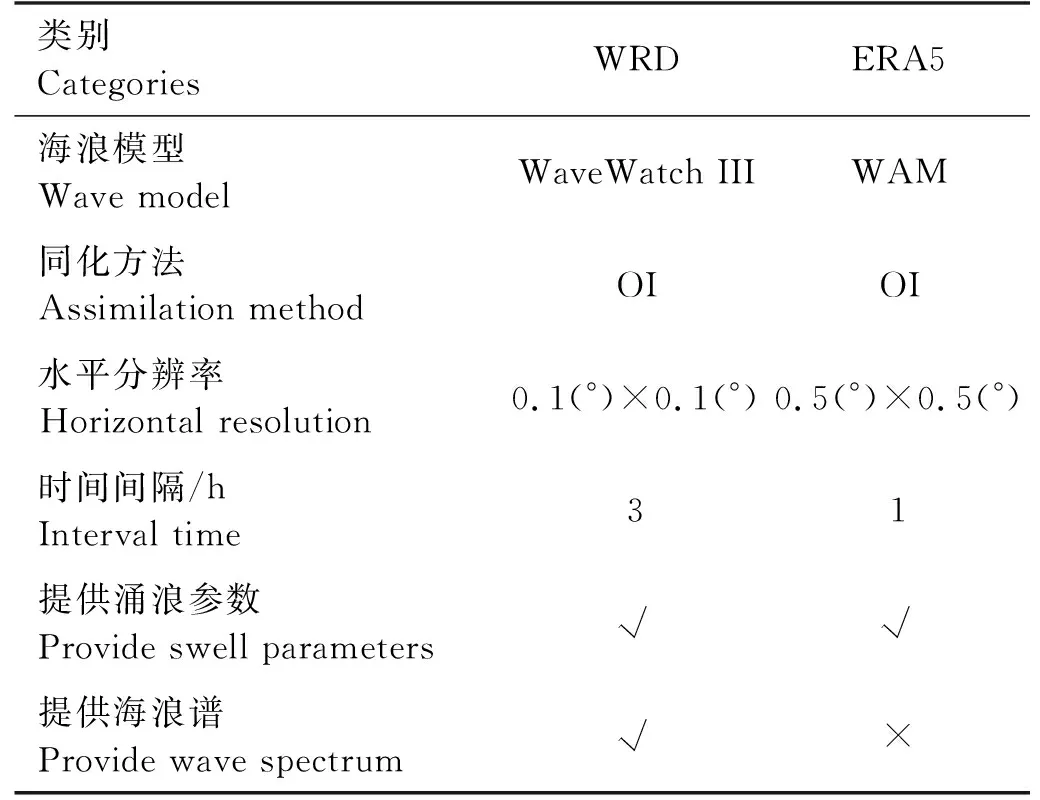
表1 WRD数据与ERA5数据对比
1.2 全球海浪再分析数据产品检验
浮标现场观测是目前最可靠的波浪观测手段,因此浮标海浪观测数据是用于海浪再分析数据产品检验的首选参照数据。图 2蓝色菱形为收集的美国国家数据浮标中心(National Data Buoy Center,NDBC)提供的76个波浪浮标站位,黄色菱形为收集的中国近海22个波浪浮标站位,涵盖了目前能够收集到的国内外主要波浪浮标数据,用于产品质量检验的波浪浮标数据时段为1998、2008和2017年,观测样本总数为186 273组,具有代表性。
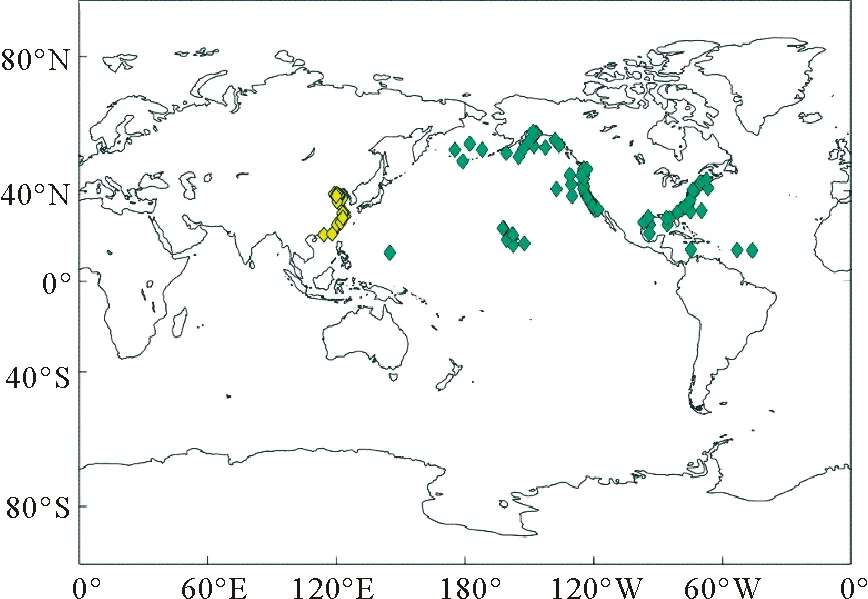
图2 全球浮标站分布
此外,考虑收集到的浮标站位主要分布在北太平洋和美国东岸地区,在南大洋缺少浮标观测,此处采用卫星海洋学存档、验证及解释数据(Archiving,Validation and Interpretation of Satellite Oceanographic,AVISO)提供的近实时全球网格化卫星观测海浪产品作为观测数据的补充,对再分析数据产品的全球分布进行检验。全球网格化卫星观测海浪产品融合了观测时段内公开发布的多颗卫星数据,在空间和时间上进行加权插值处理至全球规则网格上,最终形成空间范围180°W—180°E,-90°S—90°N,时间间隔为1天的全球有效波高分布数据集。此次检验所用的全球网格化卫星观测海浪产品时间段为2016和2017年。
对全球海浪再分析数据产品的质量评估主要基于均值偏差(Bias)、均方根误差(Root Mean Square,RMS)、相关系数(Correlation Coefficient,CC)三个参数,其具体计算方法如下:
(1)
(2)
(3)
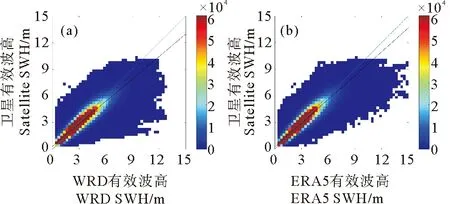
此处对本研究使用的WRD产品和ERA5产品与波浪浮标观测数据进行对比检验,以比较两类产品在数据质量上的差距。有效波高和平均周期的对比结果如图 3和表 2所示,其中,ERA5产品的有效波高(Significant Wave Height,SWH)的RMS为0.32 m,稍优于WRD产品的0.43 m,两类产品的有效波高与浮标数据相比均略偏低,WRD产品平均偏差为-0.07 m,而ERA5产品平均偏差为-0.05 m。对平均周期(Mean Wave Period,MWP)而言,WRD产品RMS为0.97 s,明显优于ERA5产品的1.66 s,其中,WRD产品平均周期较浮标数据偏低,平均偏差为-0.27 s,而ERA5产品平均周期明显高于浮标数据,平均偏差为1.38 s。
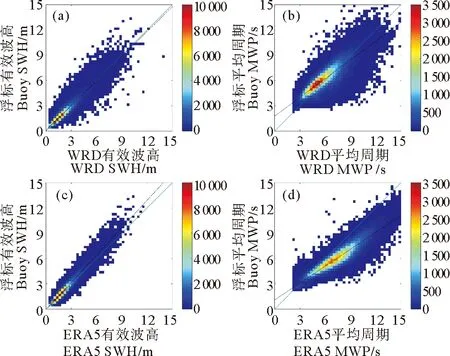
(填色:样本数。 Color: Number of sample.)
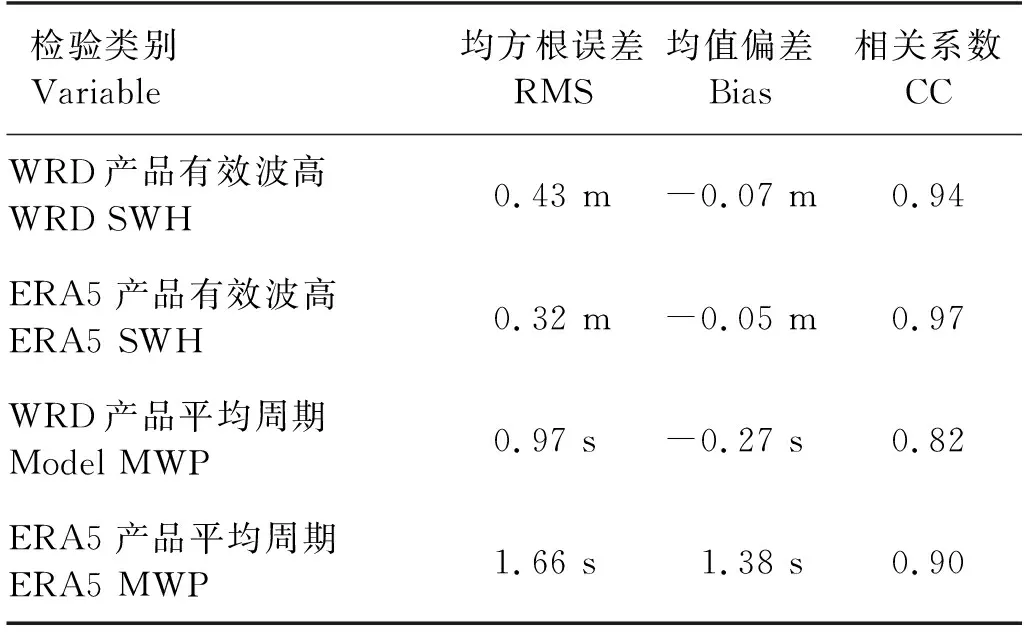
表2 数据质量检验(与浮标数据对比)
两类产品与AVISO提供的网格化全球海浪有效波高产品进行对比,整体结果如图 4和表 3所示,有效波高RMS的空间分布如图5所示。
(填色:样本数。 Color: Number of sample.)
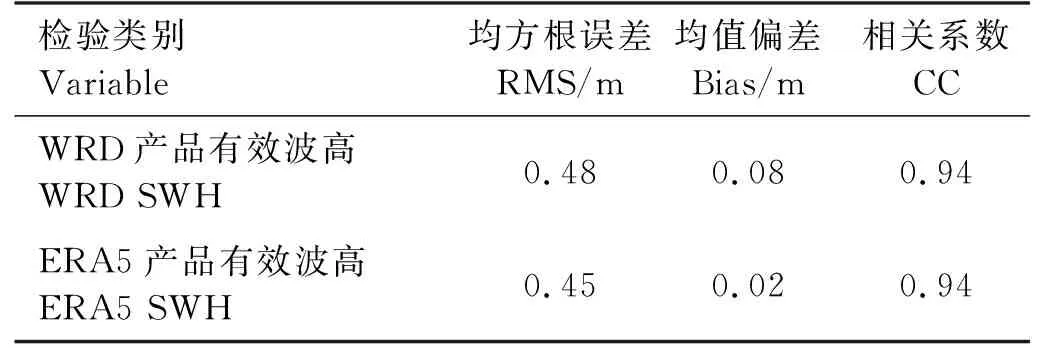
表3 数据质量检验(与卫星数据对比)
结果表明,WRD产品对有效波高的模拟质量无论是在整体上还是在空间分布上均与ERA5产品相当。
在海浪谱模型中,对于海浪有效波高(SWH),有:
(4)
其中m0是海浪谱的0阶矩,表示为:
m0=∬E(f,θ)dθdf。
(5)
式中:E(f,θ)表示海浪方向谱;f为频率分量;θ为角度分量。类似的,对于平均周期(MWP)的计算,有:
(6)
其中m2是海浪谱的2阶矩,表示为:
m2=∬f2E(f,θ)dθdf。
(7)
(4)和(6)表明模型有效波高与模型海浪谱的总能量之间存在对应关系,而模型平均周期与模型海浪谱中的能量分布存在对应关系。波高和周期的检验结果表明,WRD和ERA5产品隐含的海浪谱信息在总能量上是相近的,但在能量分布上WRD产品优于ERA5产品。由于涌浪信息的提取依赖于海浪谱的能量分布,因此本研究使用WRD产品更为合适。
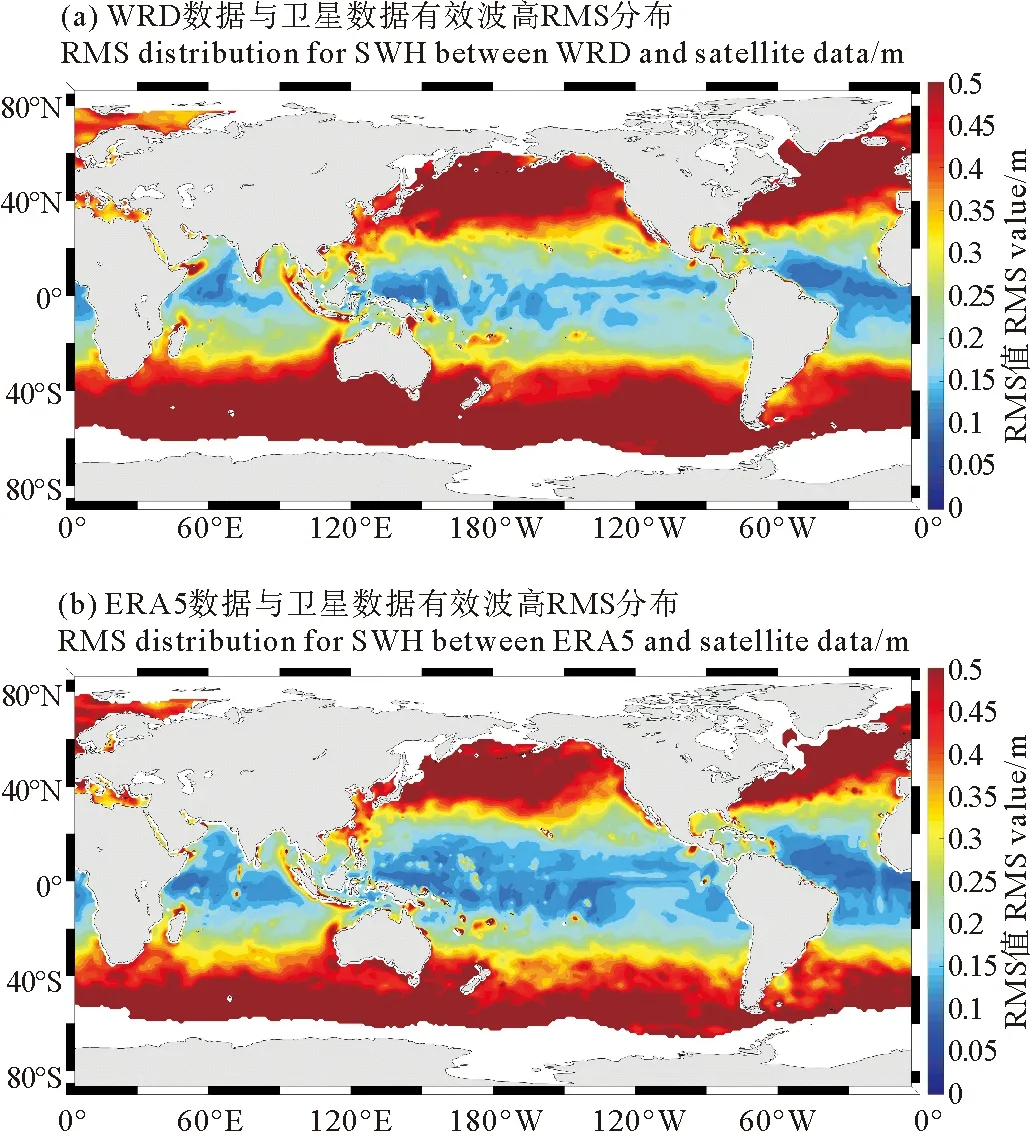
图5 全球有效波高RMS分布(与卫星数据对比)
2 数据分析方法
2.1 涌浪池的定义
“涌浪池”最初由Chen等[5]对全球海浪特征进行统计分析时提出,指涌浪事件发生频率极高的区域,由于其所用的卫星高度计和散射计数据仅包含有效波高和海表10 m风速,因此对涌浪事件的判据如下:
首先,海浪在风的驱动下从成长状态逐渐发展为充分成长状态,有理论上的风-浪充分成长关系:
(8)
式中:U为海表10 m处风速;H即为理论上的充分成长波高。
然后,根据卫星高度计观测的有效波高和散射计观测的当地风速对风浪事件和涌浪事件进行区分,认为当观测有效波高低于理论充分成长波高H时,海浪处于成长状态,当前观测点属于风浪事件,而观测有效波高高于H时,认为当前观测点受涌浪主导,属于涌浪事件。显然在此划分下,风浪事件和涌浪事件是相互独立的,对风浪事件Nw和涌浪事件Ns有Nw+Ns=N,N即为事件总数,对于涌浪事件概率Ps和风浪事件概率Pw有:
(9)
对于涌浪事件概率Ps>0.95的区域,Chen等[5]定义为涌浪池。
Chen等[5]所用的方法是参考风速作用海浪状态,在经验上的一种简单划分,其中并未考虑风向的影响,也未考虑混合浪状态下涌浪在波浪中具体的能量占比,因而该方法是一种基于统计的估计,对涌浪池的气候态分布估计具备一定的参考性,当需要分析涌浪池年际变化时,该方法并不可取。
本研究基于逐3小时30年WRD产品,对涌浪事件及涌浪池采用如下定义:
(1) 涌浪谱的定义
考虑到计算涌浪的需求,涌浪谱基于海浪二维谱,采用如下方式进行计算:首先对二维谱中各频率和方向上的能量进行分类,以E(f,θ)表示频率f和角度θ所对应的谱能量,C为与f和θ相对应的单个波的波速,当满足式(10)时,认为风无法再引起这个波的成长,此部分能量属于涌浪能量[11]。
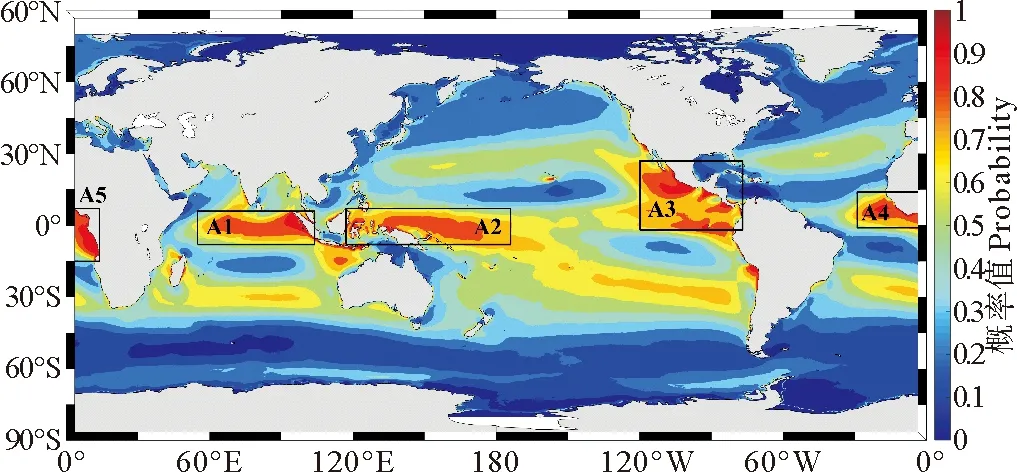
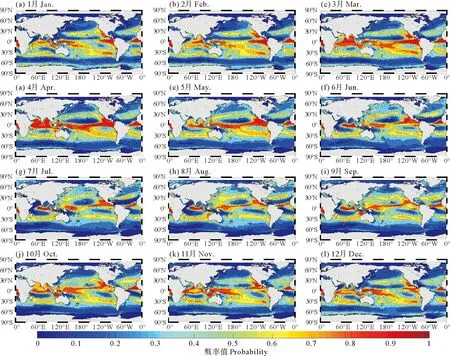
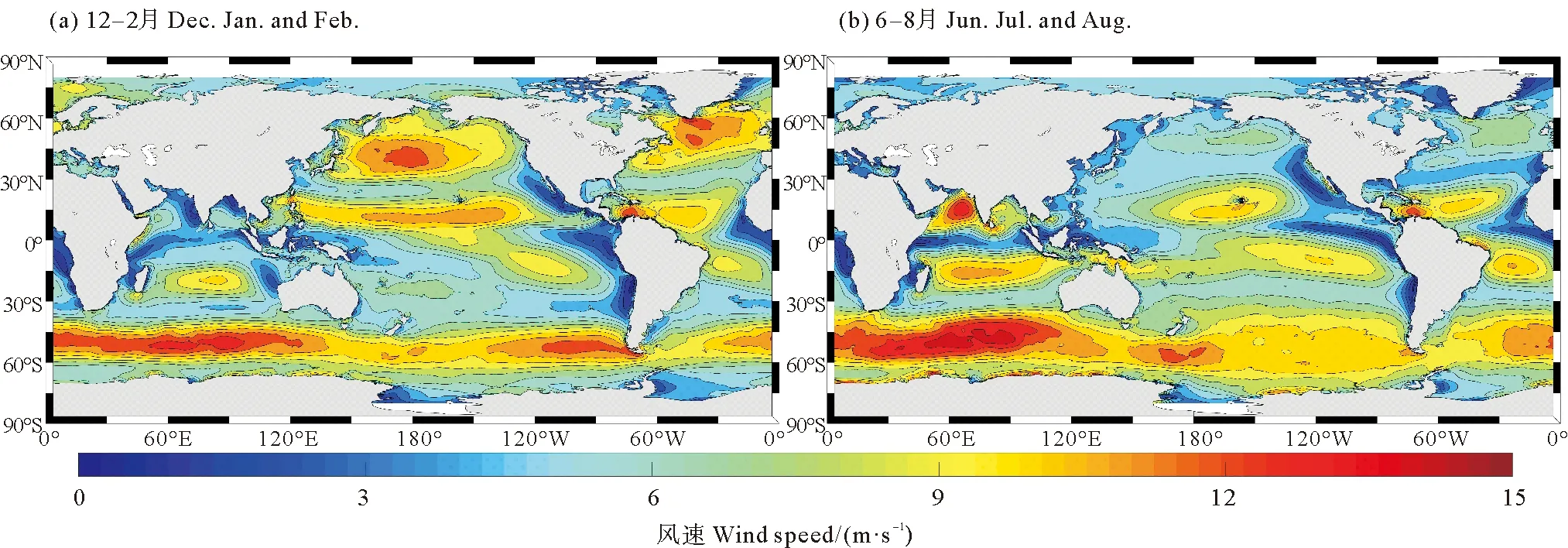
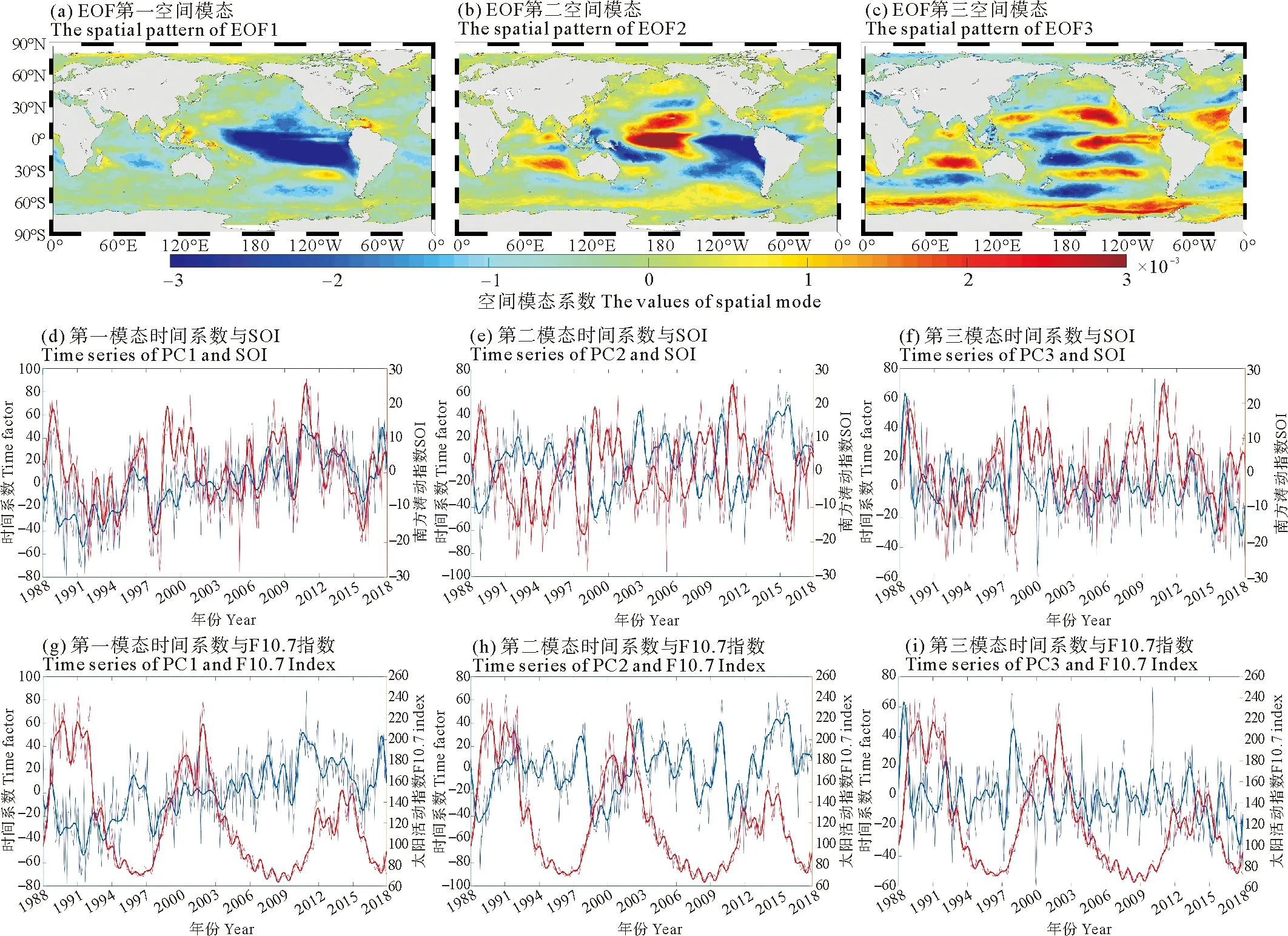
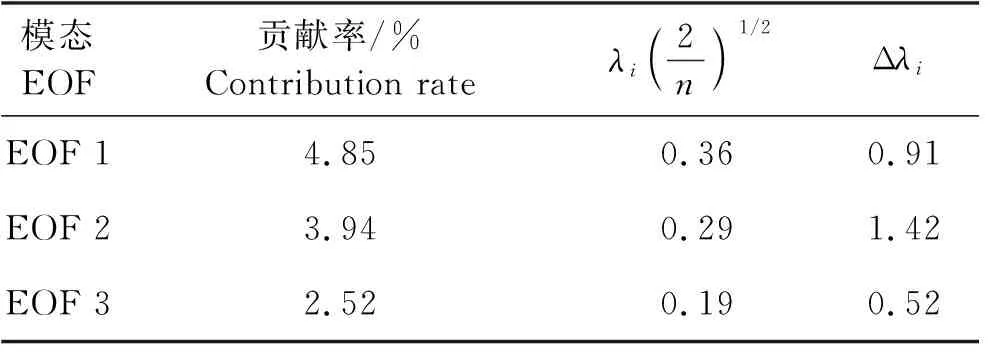
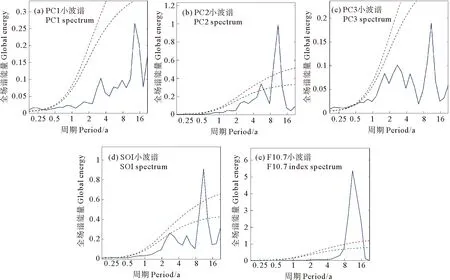
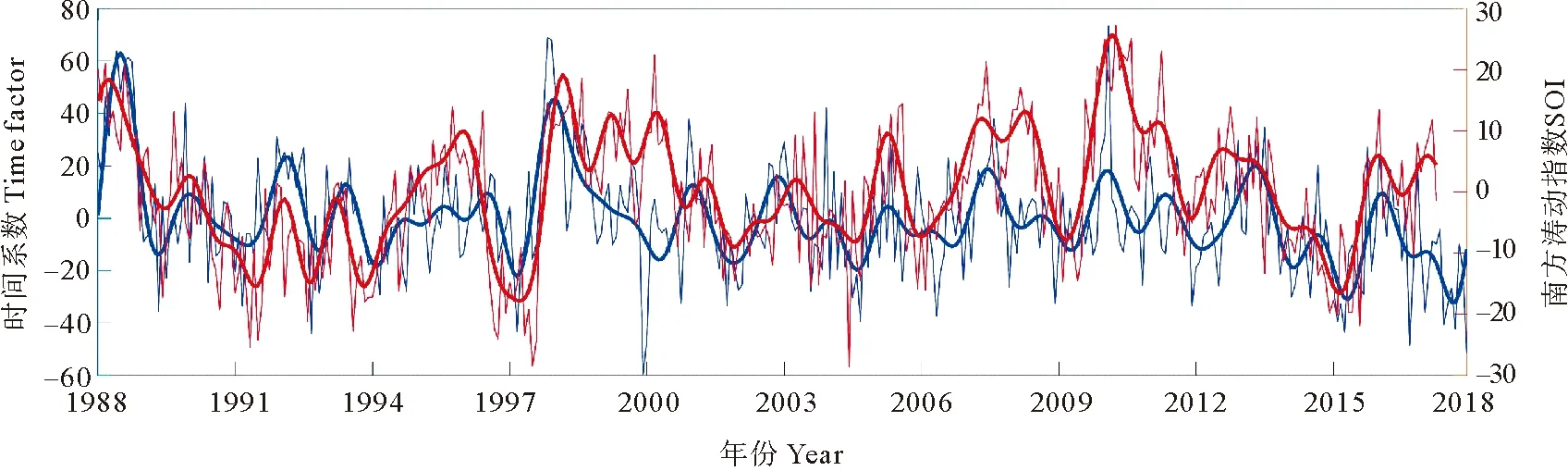
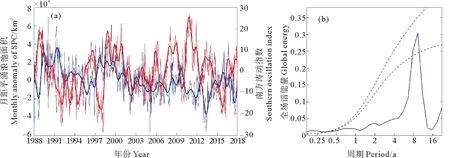
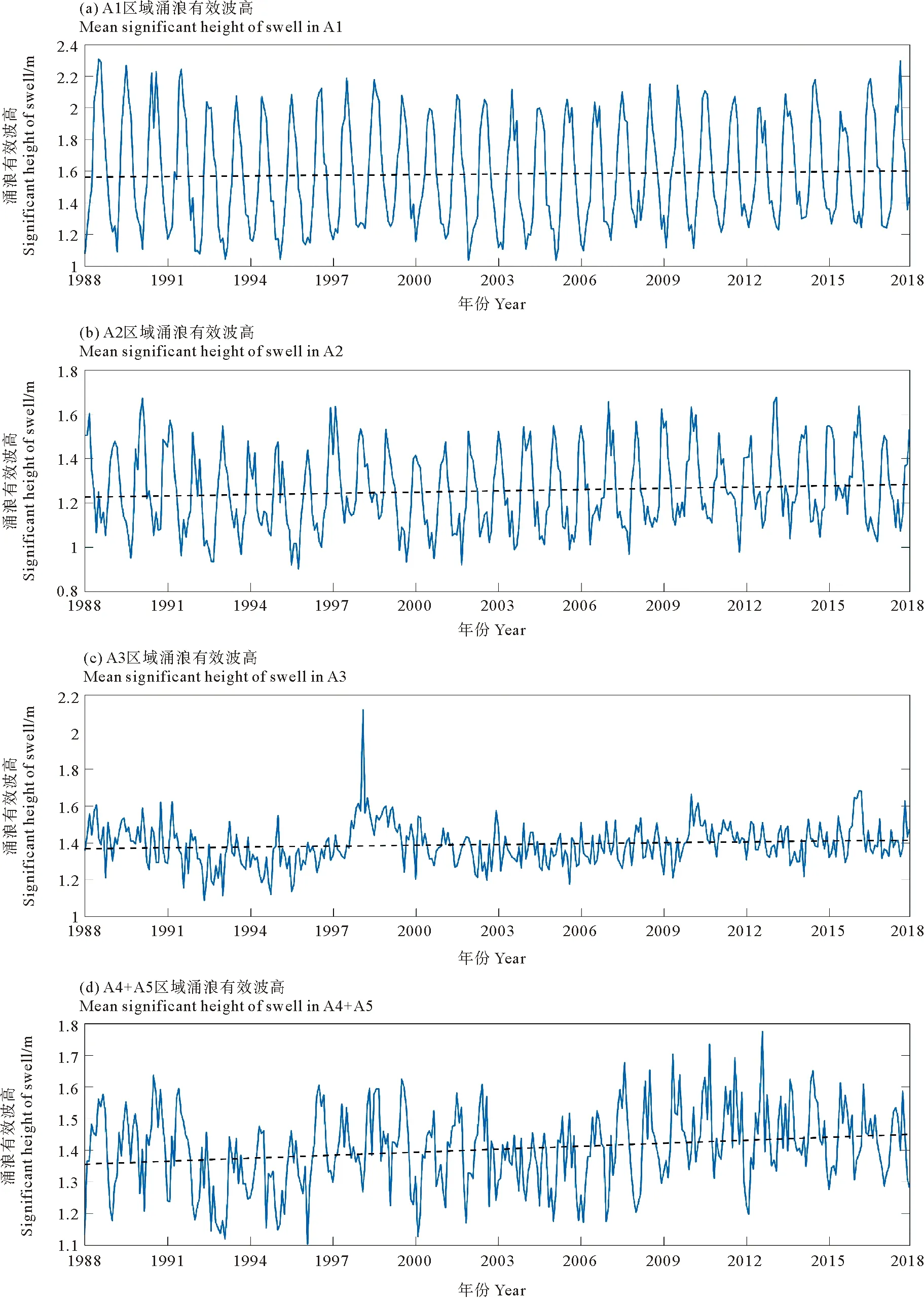
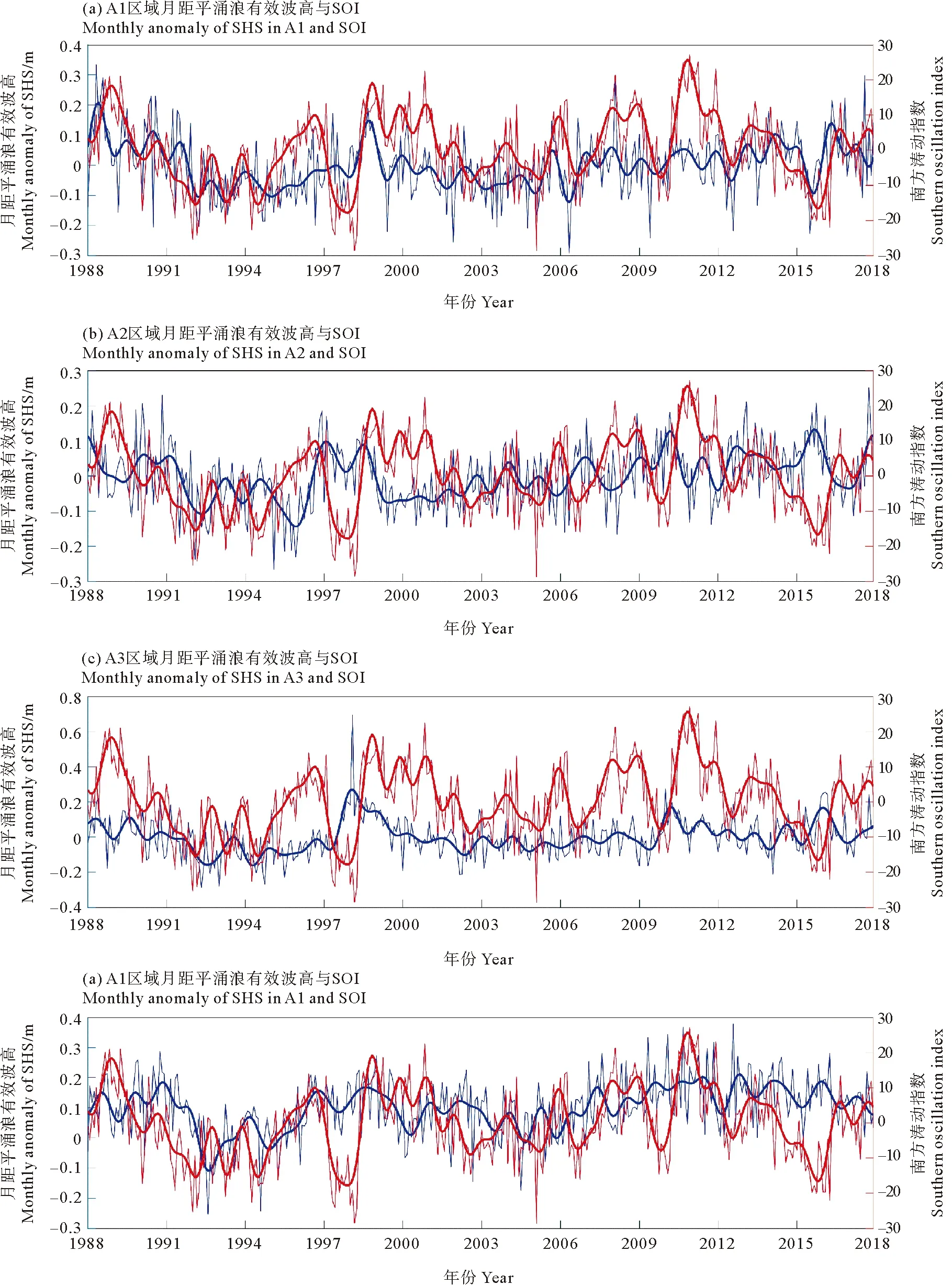
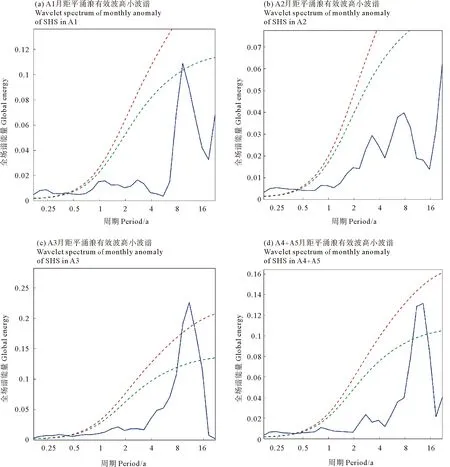
AU10cos(θ-φ) (10) 式中:U10表示海表10 m处风速;φ为风向;A为波龄因子,反映海浪的成长状态,此处设为常数1.7。对海浪二维谱在频率和角度分量上进行遍历,所有满足式(10)的谱能量构成的能量分布即为涌浪二维谱。 (2) 涌浪事件的定义 各时刻每个格点处,当涌浪能量在总能量中占比高于80%时,认为当前海浪处于涌浪主导状态,即发生了一次涌浪事件。若一段时间内存在N个时刻,则出现涌浪事件的时刻数Ns与总时刻数N的比值称为涌浪事件概率。 (3) 涌浪池的定义 对于月平均涌浪事件概率高于0.7的区域,认为该区域在该月的绝大部分时间内都处于涌浪主导状态,本文将这些区域定义为涌浪池。 本文使用经验正交函数分解法(Empirical Orthogonal Functions,EOF)和小波分析方法(Wavelet analysis)对涌浪数据进行分析,以探讨涌浪池的年际变化规律。经验正交函数分解法由气象学家Lorenz首次引入气象学分析中[12]。此方法能够将随时间变化的空间场分解为多个不随时间变化的空间模态,及与各空间模态对应的时间系数,通过将变量场的信息集中在几个主要模态上实现对原数据的降维分析,因而被广泛应用于气候研究中[13]。小波分析方法最初由Morlet等[14-15]和Grossmann等[16]在分析地震数据时所引入,相比于常用于处理平稳信号的傅里叶变换,当时域信号表现出非平稳信号特征时,小波变换能够获取各频率成分出现时段,因而被广泛应用于信号分析。 1988—2017年全球30年平均涌浪事件发生概率的分布如图 6所示。从气候态尺度来看,涌浪池主要集中在赤道区域,其中以北印度洋东侧、赤道太平洋西侧和东侧、赤道大西洋东侧涌浪事件最为频发。此外在30°S和30°N区域也存在涌浪事件频发区。图 7给出了12个月涌浪事件概率的全球分布,观察30°S和30°N出现的条带状涌浪事件频发区可发现全球涌浪池的季节变化规律:30°N区域涌浪事件在夏季(6—8月)发生频率比冬季(12—2月)高;与之对应的,30°S区域涌浪事件在夏季(12—2月)发生频率比冬季(6—8月)高。 图6 30年涌浪事件概率的平均值 图7 全球涌浪事件概率月分布 接下来从涌浪谱计算公式出发进行解释,若将大洋深水波波速公式和频散关系代入式(10),可得: fAU10cos(θ-φ) (11) 式中:g为重力加速度;f为海浪二维谱中的频率,显然当风速U10增大时,为使(11)成立,f需要满足更小的值,即更多的波处于风浪成长态,二维谱中涌浪对应的频率区间将被减小,因而计算得到的涌浪能量占比减少,相应的涌浪事件也随之减少。而各半球在冬季期间往往风速更大(见图 8),因而涌浪事件发生概率相应减少。 图8 全球风速分布 总体来说,南北半球涌浪池的出现随时间呈现周期性的反相变化趋势,各半球均以夏季为涌浪事件高发季节,全球涌浪池分布变化呈现明显的季节性特征。 对30年全球涌浪事件概率进行逐月距平以消除季节信号影响,并进行EOF分析以探讨全球涌浪池的变化规律,结果如图 9所示。其中图 9(a)、(b)、(c)对应EOF第一至第三空间模态,简记为EOF1、EOF2、EOF3,图 9(d)、(e)、(f)、(g)、(h)、(i)中的蓝色细线为与空间模态对应的逐月时间系数,简记为PC1、PC2、PC3。 从图 9(a)、(b)、(c)可发现,在EOF1中,绝大部分区域空间系数在0附近,即在第一模态中大部分区域涌浪事件概率基本不随时间变化,其变化主要发生在东南太平洋空间系数低值区。而在EOF2中,赤道太平洋中部和东部出现了一正一负相反的空间系数,这表明两区域涌浪事件概率将随时间变化呈现反向变化趋势,而在EOF3中,空间系数随纬度呈纬向条带状正负交错分布。 (蓝色细线为逐月时间系数(a)~(c),蓝色粗线为滤除1年以内周期信号的时间系数(a)~(c),红色细线为南方涛动指数(d)~(f)和F10.7指数(g)~(i),红色细线为滤除1年以内周期信号的南方涛动指数(d)~(f)和F10.7指数(g)~(i)。The blue thin line is the monthly time factor (a)~(c); The blue thick line is the time factor for filtering the periodic signal within 1 year (a)~(c); The red thin line is the monthly time series of SOI (d)~(f) and F10.7 Index (g)~(i); The red thick line is the time series of SOI (d)~(f) and F10.7 Index (g)~(i) for filtering the periodic signal within 1 year.) 表4是各模态的贡献率,从前三个模态可发现各模态贡献率相近且偏低。当模态贡献率相近时,可能存在信息混淆的情况,此时需要开展显著性检验,根据North[17]提出的检验方法,当相邻两个模态之间的贡献率差异满足时,通过显著性检验。式(12)中Δλi=λi-λi+1,表示第i个模态的贡献率λi和第i+1个模态贡献率λi+1的差异,当满足式(12)时,认为第i个模态与后续模态之间不存在信息混淆。显著性检验结果在表 4中列出,其中前三个模态均满足显著性检验。这表明在前三个模态中并未出现信息混淆的情况。 (12) 表4 各模态贡献率 此处我们猜测EOF得到的各模态贡献率相近且偏低的原因在于除季节影响外,全球涌浪事件异常受多种过程的影响,且各过程对涌浪事件异常的影响程度基本相当,并不存在某一特定过程能够主导全球涌浪事件异常,多个影响程度相当的物理过程对贡献率进行了“均摊”,使得各模态贡献率均偏低且相近。以下将对前三个模态进行分析以论证此猜测。 图10(a)、(b)、(c)是对PC1至PC3进行小波分析得到的全场小波谱,PC1至PC3全场小波谱的最大谱峰均对应11年周期,其中PC1小波谱11年周期置信水平达到0.75,PC2小波谱11年周期置信水平达到0.95,PC3小波谱11年周期置信水平达到0.70。该周期与厄尔尼诺-南方涛动(El Nio-Southern Oscillation,ENSO)的年代际振荡周期相接近[18-19]。此处选用南方涛动指数(Southern Oscillation Index,SOI)作为ENSO参考指标,SOI是厄尔尼诺和拉尼娜事件期间热带太平洋西部和东部(即南方涛动状态)之间发生的大规模气压波动的一种度量,图 10(d)是同时段内的SOI小波谱,其中存在显著的11年周期信号,且置信水平达到0.95。 (蓝线为全场小波谱,红色虚线0.95置信水平,绿色虚线0.85置信水平。The bule line is the global wavelet spectrum; The red dashed line is 0.95 confidence level; The green dashed line is 0.85.) 同时,11年周期信号也与太阳活动周期相对应,此处选用被广泛用于表征太阳活动的10.7 cm(2 800 MHz)太阳射电通量作为太阳活动指数(通常简称为F10.7指数),其小波谱如图 10(e)所示,该信号同样存在显著的11年周期特征,且置信水平达到0.95。研究表明,太阳活动与ENSO事件存在关联,主要表现为太阳11年周期活动对ENSO起着锁相作用[20-21]。 为分析全球涌浪事件异常与ENSO及太阳活动之间的相关性,此处分别将各模态时间序列与SOI时间序列和F10.7指数进行相关分析。图 9(d)、(e)、(f)中的红色细线为对应时刻的SOI时间序列,红色粗线是滤除1年以内周期信号后的SOI时间序列,蓝色细线是时间系数,蓝色粗线是滤除1年以内周期信号的时间系数,与之类似的,图 9(g)、(h)、(i)中的红色细线为对应时刻的F10.7指数时间序列,红色粗线是滤除1年以内周期信号后的F10.7指数时间序列,蓝色细线是时间系数,蓝色粗线是滤除1年以内周期信号的时间系数。 此处根据式(13)分析两者之间的线性相关性,并开展显著性检验,线性相关条件下的显著性检验方法是构建一统计量T: (13) 式中:r表示两者之间的相关系数;n表示样本数量。此时T满足自由度为n-2的t分布(t-distribution)。由此即可计算得到相关系数的置信水平。 SOI与时间系数的相关分析结果表明,对于PC1,两者存在相近的变化趋势,两者相关系数为0.55,而PC2与SOI变化趋势相反,两者相关系数为-0.77,PC3与SOI并没有表现出直接的相关关系,而是存在滞后关系,将SOI提前9个月(见图 11)。从图11中可发现其与PC3呈现相似的变化趋势,两者相关系数为0.53。经显著性检验,以上相关系数均达到0.95置信水平。 图11 SOI (提前9个月)与第三模态时间系数 对F10.7指数与时间系数之间的相关分析结果表明,仅PC1与F10.7指数之间存在较好的负相关关系,相关系数为-0.41且置信水平达到0.95。PC2与F10.7指数之间的相关性较弱,相关系数为-0.15,置信水平达到0.95,而PC3与F10.7指数之间不存在相关性。 以上结果表明,全球涌浪事件异常的年际变化在前三个模态主要表现为11年周期特征,虽然该周期信号与南方涛动和太阳活动的周期信号相似,但相关分析结果表明仅第一模态与太阳活动之间存在一定的负相关性,其余模态与太阳活动关联较弱。全球涌浪事件异常主要与南方涛动之间存在关联,且响应关系复杂,具体表现为在时间变化上涌浪事件发生概率与SOI存在同位相、反位相、位相滞后等多种响应关系,这在一定程度上也印证了先前对各模态贡献率均较低且相近的原因的猜测,即存在多个影响程度相当的过程对贡献率进行了“均摊”,在前三个模态中,表现为涌浪事件异常和南方涛动存在多种不同位相组合上的响应关系,南方涛动对涌浪事件发生概率起着调制作用。 对30年全球逐月涌浪池面积进行计算,并进行月距平以滤除季节影响,将其进行小波分析并与SOI进行相关分析,结果如图 12所示。全球涌浪池面积异常呈现10年的变化周期,且与SOI之间存在一定程度的负相关,两者相关系数为-0.30且置信水平达到0.95。 ((a)月距平涌浪池面积与南方涛动指数,蓝色细线为月距平涌浪池面积,蓝色粗线为滤除一年以内周期信号的距平涌浪池面积;红色细线为南方涛动指数,红色细线为滤除1年以内周期信号的南方涛动指数。(b)月距平涌浪池面积小波全场谱。蓝色线为全球小波频谱,红色线为0.95置信水平,绿色线为0.85置信水平。(a) Monthly anomaly of SPC and SOI, blue thin line is the monthly anomaly of SPC and the blue thick line is the anomaly of SPC for filtering the periodic signal within 1 year; The red thin line is the monthly time series of SOI; The red thick line is the time series of SOI for filtering the periodic signal within 1 year. (b) Global wavelet spectrum for monthly anomaly of SPC; The bule line is the global wavelet spectrum; The red dashed line is 0.95 confidence level and the green dashed line is 0.85.) 对涌浪池内的波高变化规律进行分析,根据全球30年平均涌浪事件发生概率,划出A1—A5五个涌浪事件多年频发区作为涌浪池区域(见图6),区域对应经纬度范围如表 5所示,其中A4、A5均为大西洋东侧涌浪池,在分析时视为同个区域,记为A4+A5,将各区域内涌浪波高均值作为特征值,分析各涌浪池内涌浪强度的年变化趋势。各涌浪池内涌浪有效波高(Significant height of swell,SHS)时间序列如图 13所示,其中,A1、A2区域在亚洲季风区影响范围内,表现出明显的年周期特征,A3区域年周期信号较弱。 表5 涌浪区范围 将波高序列进行线性回归以分析各涌浪区涌浪波高的年际变化趋势,如图 13中黑色虚线所示。线性回归结果表明各区域涌浪有效波高在30年内呈现极缓慢的增长趋势,其中以赤道大西洋东侧(A4+A5)增长最快,达到10-4m,北印度洋东侧(A1)增长最慢, 为0.4×10-4m。由于此处线性趋势极为微弱,因此需进行显著性检验。对时间序列的趋势性检验可采用Mann-Kendall趋势检验[22-23](简称MK检验),该检验方法常用于在统计上确定变量随时间变化的单调性趋势。其方法是将n个样本按时间顺序进行依次排列,则有X={x1,x2,x3,…,xn},对变量xi和xj(此处1≤j (14) (15) 对S,有方差Var(S)=n(n-1)(2n+5)/18。随后计算MK的Z值: (16) 最后对ZMK进行Z检验,即可得到置信水平。经检验,A1区域增长趋势置信水平为0.85,A2区域为0.97,A3区域为0.99,A4+A5区域为0.99。 图13 各区域涌浪有效波高平均值时间序列 图14中蓝色细线是各区域涌浪有效波高时间序列进行逐月距平后的波高异常值。这里对各区域波高异常值进行小波分析,全场小波谱如图15所示,可以看到除A2区域外,各区域均表现出了11年周期,将滤除1年以内信号的距平涌浪有效波高(Anomaly of significant height of swell,ASHS)与SOI进行滞后相关分析以讨论两者之间在时间位相上的响应关系,结果如表6所示:除A2区域外,其他区域涌浪波高的异常变化与SOI之间存在不同时间位相上的相关关系,其中以赤道太平洋东侧涌浪波高异常与SOI相关性最大,为0.51,其次为北印度洋东侧,相关性为0.43,赤道大西洋东侧为0.37。经显著性检验,以上相关系数均达到0.95置信水平。 (蓝色细线为月距平涌浪有效波高,蓝色粗线为滤除1年以内周期信号的距平涌浪波高,红色细线为月平均SOI序列,红色粗线为滤除1年以内信号的SOI序列。The blue thin line is the monthly anomaly of SHS; The blue thick line is the anomaly of SHS for filtering the periodic signal within 1 year; The red thin line is the monthly time series of SOI; The red thick line is the time series of SOI for filtering the periodic signal within 1 year.) 图15 各区涌浪波高异常小波全场谱 表6 滞后相关分析 对A1区域,亚洲夏季风包含的Findlater急流[24]会引起北印度洋波高的显著提升[8],而亚洲夏季风与ENSO之间存在密切关联。当夏季季节内振荡与ENSO存在不同的相位组合时,北印度洋波浪特征会出现明显差异[25],因而该区域涌浪特征与ENSO存在关联。而在A2区域,东太平洋海表风异常在ENSO事件的发展中起到重要的调制作用[26],这在一定程度上将东太平洋涌浪与ENSO建立了联系。在A4+A5区域,赤道大西洋存在的赤道大西洋振荡对ENSO存在响应,Latif和Barnett[27]基于混合耦合模型提出出现ENSO极端事件时,赤道大西洋盛行风异常,Latif和Grötzner[28]使用观测数据和全球大气-海洋环流模型指出了赤道大西洋振荡对ENSO的滞后响应关系。 此外有研究表明,在热带西太平洋海域,风应力的异常会引起表层高温海水异常输运,使赤道太平洋海表温度出现异常,这在ENSO循环中有着至关重要的作用[29-30]。此外,风异常引起的海温变化会影响台风的特性,进而对西北太平洋的波浪特征产生影响[31]。以上研究均指出了海表温度异常与风之间的响应关系,因此此处尝试将海洋中使用海表温度异常来表征厄尔尼诺现象的Nino指数与A2区域涌浪波高异常进行相关分析,此处选用空间上与A2最为接近的Nino4指数(对应160°E—150°W,5°S—5°N区域海温异常)作为滞后相关分析的对象,结果表明,A2区域涌浪波高异常滞后Nino4指数1个月时两者相关性最高,为0.28,且置信水平达到0.95。 本研究基于自主研制的海浪再分析系统和基于海浪二维谱的涌浪谱提取方法,完成了1988—2017年共30年的全球海浪再分析产品制作,经浮标资料和卫星融合资料检验,产品在有效波高方面与ERA5产品质量相当,在平均周期方面该产品优于ERA5产品,产品质量可靠,适合用于涌浪分析。本文基于该数据集对全球涌浪池分布及年际变化进行分析,主要结论如下: (1) 全球涌浪池主要分布在赤道地区,且多分布于大洋东边界。南北半球30°S和30°N附近区域存在条带状分布的涌浪事件高发区,对南北半球而言,涌浪池均在夏季出现频繁,在冬季出现较少。全球涌浪池在时间上呈现明显的季节变化特征。 (2) 对30年全球涌浪事件概率进行月距平,滤除季节信号后进行EOF分析,结果表明,全球涌浪事件概率受多种因素的共同作用,在时间系数上与SOI和F10.7指数存在相近的11年周期信号。相关分析结果表明,全球涌浪异常主要与南方涛动相关,与太阳活动关系较弱。在前三个模态中,全球涌浪事件概率与SOI在时间上存在同位相、反位相、位相滞后的响应关系,两者之间关联较为复杂。涌浪池面积异常的年际变化呈现10年周期特征,且与SOI之间存在一定程度的负相关,两者相关系数为-0.30。 (3) 对北印度洋东侧、赤道太平洋西侧、赤道太平洋东侧、赤道大西洋东侧4处涌浪池内的涌浪波高进行分析,结果表明,各区域内涌浪波高呈缓慢升高趋势,其中以赤道大西洋东侧增长速度最大,为10-4m·a-1。对各区域涌浪波高异常进行小波分析,结果表明,除赤道太平洋西侧外,其余区域涌浪波高异常均存在与SOI相似的11年周期。将涌浪波高异常与SOI进行滞后相关分析,结果表明,除赤道太平洋西侧外,各区涌浪波高异常与SOI呈现不同时间位相的相关性,其中北印度洋东侧和赤道太平洋东侧涌浪波高异常领先于SOI,相关系数分别为0.43和0.51,而赤道大西洋东侧涌浪波高异常滞后于SOI,相关系数为0.37。将表征海表温度异常变化的Nino4指数与赤道太平洋西侧涌浪波高异常进行滞后相关分析,结果表明两者存在一定相关性,相关系数为0.28,且涌浪波高异常滞后Nino4指数。总体而言,全球涌浪池内涌浪波高的异常变化与ENSO事件存在关联。 不同于以往涌浪池研究所用的基于经验公式和有效波高的涌浪事件评估方法,本研究对涌浪信息的提取基于各时刻的海浪二维谱,因而能够获取较为精确的逐时刻涌浪谱信息,填补了过去对全球涌浪池的研究仅含气候态特征而不含年际变化的空白,能够为今后涌浪相关研究及海-气相互作用研究提供一定的参考。2.2 分析方法
3 数据分析与讨论

4 结论
