基于UWB定位融合的机器人路径跟踪控制技术

庞凌锋，蔡文郁，朱 艺，张美燕

(1.杭州电子科技大学电子信息学院，浙江 杭州 310018；2.浙江水利水电学院电气工程学院，浙江 杭州 310018)

0 引 言

随着机器学习、人工智能技术的发展，机器人的应用日趋成熟，机器人路径跟踪是主要研究方向之一。目前常用的机器人路径跟踪方法大致分为运动学模型、动力学模型和无模型[1]。运动学模型跟踪方法需实时获取机器人的位姿信息，输出相应的运动状态[2]。由于机器人结构复杂，环境又具有未知性，因此，该方法易受外界干扰，鲁棒性较差。文献[3]使用模糊比例积分微分(Proportion Integral Differential,PID)配合运动学模型完成了3种较为复杂的路径；文献[4]中，机器人配合视觉追踪布置的引导线来完成跟踪。动力学模型跟踪方法主要依据牛顿第二定律，假设机器人为1个质点，对机器人进行受力和动力学分析。文献[5]采用比例积分控制器和滑膜控制，通过仿真实验完成了路径的跟踪，提高了动力学模型的精度；文献[6]运用模型预测和速度PID进行路径跟踪，具有良好的跟踪性能。但是，动力学模型对传感器精度的要求十分高。无模型跟踪方法采用除运动学模型和动力学模型以外的方法来完成路径的跟踪，主要算法有神经网络控制算法、模糊控制算法、纯追踪算法、基于距离的跟踪算法等。神经网络控制算法是一种模拟生物神经组织处理外界事物的智能算法。文献[7]使用神经网络分析跟踪的路径图像，配合控制算法完成机器人路径的跟踪，跟踪误差小，但神经网络的训练成本高，需要大量数据。模糊控制算法是一种运用模糊数学知识对模糊现象进行识别判断的智能算法，该算法不依赖纯粹的数学模型，但对控制目标的定义较难。文献[8]采用进化学习算法学习不同的模糊控制方案，完成了编队机器人的路径跟踪。纯追踪算法通过模拟驾驶员的驾驶，根据驾驶过程的前视距离得到期望路径上的预瞄点，规划出机器人途经的弧线和转向角，进行路径的跟踪。文献[9]通过改进转向角的计算方法，实现了多段折线的跟踪。但在高速情况下，纯追踪算法难以进行跟踪。基于距离的跟踪算法主要依据与目的地的距离及方向关系来完成路径跟踪。文献[10]使用射频识别(Radio Frequency Identification,RFID)模块作为导航点，实现了基于距离的跟踪，但无法跟踪较为复杂的曲线。本文提出一种基于距离定位的分段PID路径跟踪算法，运用超宽带技术(Ultra Wide Band,UWB)辅助定位，对路径离散化并组合得到分段路径，再对每个分段路径进行PID路径跟踪，提高了跟踪效果。

1 机器人系统模型

假设机器人为轮式机器人，系统模型如图1所示。以A1基站为原点搭建坐标系，基站A1至A2方向为x轴方向，A1至A4方向为y方向，A3位于偏离x轴45°方向的直线上。轮式机器人机械结构如图1中R1和R2，由后方2个驱动轮和前方1个从动轮组成。通过控制2个驱动轮电机的转速产生差速，从而控制机器人的运动。通过传感器可以获得轮式机器人的位置和航向角信息，但无法获得机器人的速度和驱动轮转速。机器人的位姿信息P定义为：

(1)

式(1)中，(xr,yr)为机器人的坐标位置，θr为机器人航向与x轴的夹角，r为机器人的状态。图1中，R1的位姿信息表示为(x1,y1,θ1)，R2的位姿信息表示为(x2,y2,θ2)。

图1 轮式机器人的系统模型

2 分段PID跟踪算法

2.1 基于距离的跟踪算法

文献[10]提出的基于距离的路径跟踪算法将RFID标签作为导航点，且导航点位置已知，机器人根据当前坐标N(xnow,ynow,θnow)与下一个目标导航点D(xdst,ydst,θdst)之间规划出2个临时导航点A和B，行驶距离为m，单位为m。机器人以θnow为航向，行驶距离m至导航点A，通过RFID测距技术获得离导航点A的距离dA，再旋转θAB并行驶m至导航点B，通过RFID测距技术获得离导航点的距离dB，B到目标导航点D的航向角θdst的计算公式如下：

(2)

采用基于距离的路径跟踪算法跟踪路径时，由于引入了2个临时导航点来计算航向角，使得曲线变得并不平滑，如果路径比较复杂，则需要布置更多的导航点，增加硬件成本。故本文对航向角和定位方式进行改进，采用UWB定位技术对机器人进行定位。首先，根据图1部署的4个基站搭建参考坐标系；然后，运用文献[11]提出的三边定位算法计算每个基站与机器人的测距值，并采用文献[12]提出的定位精度的几何稀释分析算法得到机器人的定位坐标(xr,yr)；最后，根据机器人当前坐标和目标坐标，推算出航向角θdst。和基于距离的路径跟踪算法相比，减少了计算量和节点数量，避免了建立临时导航点带来的不平滑移动。本文算法的航向角θdst的计算公式如下：

(3)

其中，disY=(ydst-ynow)，disX=(xdst-xnow)。

2.2 基于距离定位的分段PID路径跟踪算法

基于距离的跟踪算法主要依据与目的地的距离及方向关系来完成路径的跟踪，难以跟踪复杂路径。PID控制算法是机器人路径跟踪中常用的控制算法，但面对复杂路径时，其跟踪误差不断累积，路径跟踪效果较差[13]。为此，本文使用PID控制算法配合UWB定位进行路径的跟踪，提出一种基于距离定位的分段PID路径跟踪算法，主要流程如图2所示。获取路径S后，进行离散采样获得离散路径Se，对离散路径进行组合，组成分段路径，随后进行路径跟踪，不断获取定位数据，在每段开始时，先调整航向角，再对每段进行PID路径跟踪，直至完成所有路径的跟踪。

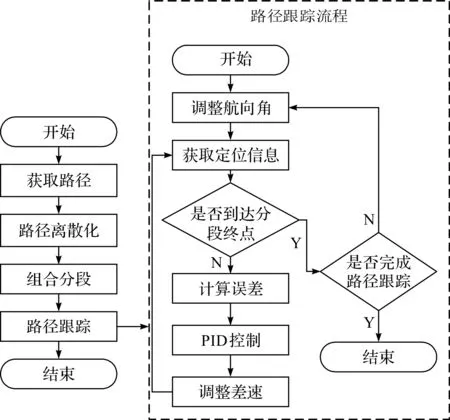
图2 基于距离定位的分段PID路径跟踪算法流程

对跟踪路径S进行采样离散化，得到离散化路径Se，Se定义如下：

(4)

式中，pn为第n个离散路径点，在坐标系中的坐标为(xn,yn)。

路径采样过程中，采样路径的相邻2个点(xj,yj)和(xj+1,yj+1)的曲率ξ为：

(5)

(6)

式中，d为路径采样间隔值，ξ0为曲率阈值，式(6)依照式(5)中曲率ξ与曲率阈值ξ0的关系决定路径的采样方式。

路径离散化后，定义t为粗组合参数，对每t个点进行粗组合，再对组合后的每个分组的角度变化进行分析。每个粗分组的第1个点与第2个点组成参考向量l，余下的第i个点与第i-1个点组成向量li，分别计算li与l之间的角度θi，如果第i点的计算角度θi大于阈值角度θth，则将第i点前面的点细分为一组，后面的点依旧重复上述过程，完成对粗组合的细分，最终将路径分为多段，再采用增量PID对每段路线进行路径跟踪。θi的计算公式如下：

(7)

基于距离定位的分段PID路径跟踪算法PID控制公式如下：

(8)

(9)

式(8)中，计算机器人当前位置(xnow,ynow)与每个分段离散点之间的差值，取其中最小差值作为PID误差e(k)，其中λ为分段的离散点个数，k为采样时间序列号，e(k)为第k次采集的误差值。将e(k)代入式(9)，得到机器人在追踪曲线时需要调整的角度的映射值u(k)，其中Kp为比例参数，Ki为积分参数，Kd为微分参数。

3 实验结果与分析

3.1 实验环境

双轮机器人的控制电路如图3所示。由28.0 V电池供电，经电源转化芯片TPS5430将28.0 V转化为5.0 V，为电机驱动供电；5.0 V经电源转化芯片MIC29302AWU转化为3.3 V，为主控STM32H750、UWB模块DW1000供电、姿态传感器MPU9250和WIFI模块ESP8266供电。STM32H750从DW1000获得与基站的测距值，从MPU9250获取航向角，通过ESP8266发送数据和接收指令，控制左右电机驱动使得机器人运动。双轮机器人实物如图4所示。

图3 双轮机器人控制电路

图4 双轮机器人实物

实验中，4个基站按图1所示摆放，基站A1，A2，A3，A4的坐标分别为(0,0)，(10,0)，(10,10)，(0,10)，实验场地大小为15 m×15 m，曲率阈值ξ0为2.5，阈值角度θth为90°，PID算法参数Kp，Ki，Kd分别为400，200，100。

3.2 轨迹跟踪实验

轨迹跟踪实验中，双轮机器人保持低速行驶，分别使用基于距离定位的分段PID路径跟踪算法和PID路径跟踪算法在直线和正弦曲线路径中进行跟踪，跟踪过程中传感器采样到的定位误差依据式(8)计算得出，且采样间隔距离d为0.2 m，粗组合参数t为5。直线运动中，机器人从(1.0,1.0)移动至(8.5,8.5)，航向为y轴正方向。收到指令后，机器人进行路径跟随，2种算法的跟踪轨迹如图5(a)所示，传感器采集到的每个点对应的误差如图5(b)所示。

图5 直线路线跟踪轨迹及误差分析

从图5(a)可以看出，基于距离定位的分段PID路径跟踪算法的跟踪曲线优于PID跟踪算法。根据图5(b)数据，运用式(8)计算得出PID跟踪算法的平均误差为14.59 cm，标准差为11.91 cm，分段PID路径跟踪算法的平均误差为10.08 cm，标准差为10.15 cm。综上分析可知，在直线运动跟踪中，基于距离定位的分段PID路径跟踪算法的跟踪效果优于PID路径跟踪算法。

曲线运动中，机器人从(0,3.5)出发，航向为y轴正方向。收到指令后，机器人进行路径跟随，2种算法的跟踪轨迹如图6(a)所示，传感器采样到的每个点对应的误差如图6(b)所示。

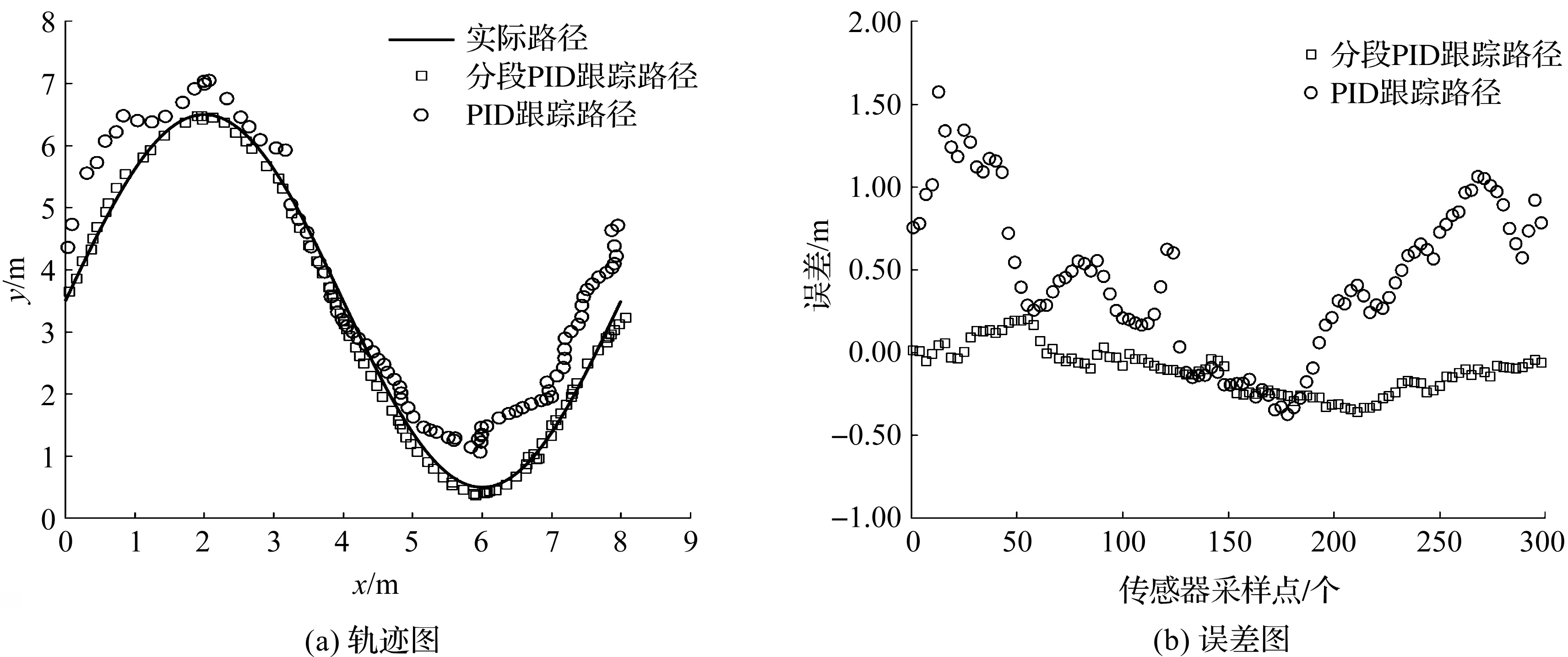
图6 正弦曲线路线跟踪轨迹及误差分析

从图6(a)可以看出，基于距离定位的分段PID路径跟踪算法的跟踪曲线优于PID跟踪算法。根据图6(b)数据计算得出PID跟踪算法的平均误差为62.49 cm，标准差为23.98 cm，分段PID路径跟踪算法的平均误差为18.43 cm，标准差为15.68 cm。综上分析可知，在曲线运动跟踪中，基于距离定位的分段PID路径跟踪算法的跟踪效果优于PID路径跟踪算法。

取采样间隔d为0.2 m，粗组合参数t分别取5，8和10，采用基于距离定位的分段PID路径跟踪算法对图6(a)中的曲线进行跟踪，跟踪结果如图7(a)所示，采样到的每个点对应的误差如图7(b)所示。

图7 不同分段路线跟踪轨迹及误差分析

从图7(a)可以看出，粗组合参数t越小，路径的跟踪效果越好。根据图7(b)中的数据计算得出，t为5时的平均误差为18.43 cm，标准差为15.68 cm；t为8时的平均误差为19.54 cm，标准差为14.91 cm；t为10时的平均误差为23.31 cm，标准差为15.91 cm。因此，粗组合参数t越小，算法的误差越小，跟踪效果越好。

取粗组合参数t为5，采样间隔d分别取0.2 m，0.4 m和0.6 m，采用基于距离定位的分段PID路径跟踪算法对图6(a)中的曲线进行跟踪，跟踪结果如图8(a)所示，采样到的每个点对应的误差如图8(b)所示。

图8 不同离散化跟踪路线轨迹及误差分析

从图8(a)可以看出，d越小，路径的跟踪效果越好，根据图8(b)数据计算得出，d为0.20 m时的平均误差为18.43 cm，标准差为15.68 cm；d为0.40 m时的平均误差为21.57 cm，标准差为16.55 cm；d为0.60 m时的平均误差为26.10 cm，标准差为17.63 cm。因此，采样间隔d越小，算法的误差越小，跟踪效果越好。

采用基于距离定位的分段PID路径跟踪算法进行巡回扫描路径的跟踪，跟踪的巡回扫描路径的扫描间距为0.60 m，机器人初始位于(1.2,1.2)的位置，航向为y轴正方向，采样间隔距离d为0.2 m，粗组合参数t为5。路径跟踪结果如图9(a)所示，传感器采样到的每个点对应的误差如图9(b)所示。

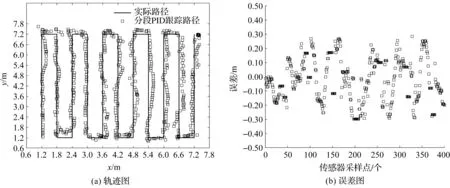
图9 巡回扫描跟踪轨迹的路线轨迹及误差分析

从图9(a)可以看出，路径的跟踪效果良好，根据图9(b)数据计算得到的跟踪平均误差为13.38 cm，标准差为27.38 cm。结果表明，基于距离定位的分段PID路径跟踪算法在跟踪复杂曲线时效果良好。

4 结束语

本文设计了一套基于UWB定位的轮式机器人系统，并提出一种基于距离定位的分段PID路径跟踪算法，跟踪效果优于仅使用PID技术跟踪算法。采用本文算法进行路径跟踪时，分段越少，采样间隔越近，跟踪误差越小。但是，本文算法对曲率变化频繁路线的跟踪效果稍差，后续将优化离散路径的组合方式，得到更符合机器人运动的分段路径，进一步研究UWB与其他传感器的融合定位方式，以提高跟踪过程的定位精度和跟踪鲁棒性。