基于生成对抗网络的伪码调相脉冲多普勒引信引导式干扰方法

2022-12-01李剑锋闫晓鹏郝新红于洪海

兵工学报 2022年10期

李剑锋，闫晓鹏，郝新红，于洪海

(北京理工大学机电动态控制重点实验室，北京 100081)

0 引言

引导式干扰是通过侦察手段获取干扰对象的频率、调制类型及参数等信息，以此针对性构造干扰信号，达到使无线电引信产生早炸的目的[1]。伪码调相脉冲多普勒引信对回波进行距离门选通以及伪随机码二次相关处理，使得引信具有较强抗噪声调幅和调频等引导式干扰性能，以及较好的速度与距离分辨能力[2-4]。为了实现对伪码调相脉冲多普勒引信的有效干扰，相关学者针对伪码调相脉冲多普勒引信提出了不同的参数提取方法，文献[5-8]利用3阶自相关函数及2阶循环统计量对伪码调相信号进行估计。但这些方法在低信噪比环境下难以精准的获取信号参数及特征，传统方法重构的伪码调相脉冲多普勒引信干扰信号能力不足，因此对伪码调相脉冲多普勒引信的干扰效果并不理想。

为能够在低信噪比环境下提高对伪码调相脉冲多普勒引信的干扰效率，提出了一种基于生成对抗网络(GAN)[9]的伪码调相脉冲多普勒引信引导式干扰方法，利用生成对抗网络对无线电引信中频信号进行重构，以此生成干扰信号对无线电引信进行引导欺骗式干扰。GAN是人工智能领域中的生成式模型，已经广泛应用于图像生成、语音生成等领域，并取得了非常好的效果[10-15]。杨龙等[16]、于浩洋等[17]将GAN应用雷达对抗中，并取得了很好的效果；向亚丽等[18]提出将GAN用于噪声干扰消除，仿真验证了该方法的优越性。然而，无线电引信干扰对实时性要求很高，一定程度上限制了深度学习方法在无线电引信干扰技术上的应用。

近年来，随着人工智能的发展与芯片运算能力的大幅提升，已经基本具备在极短时间内完成信号学习的能力，使得GAN等深度学习方法在引信干扰中应用逐渐成为可能。因此，本文将GAN网络移用于引信干扰波形重构中，以提高引信干扰的有效性。该方法能够在低信噪环境下精准的重构干扰信号，达到理想的干扰效果，仿真和实验结果表明，在低信噪比环境下干扰效果优于传统的引导式干扰。

1 伪码调相脉冲多普勒引信工作原理

伪码调相脉冲多普勒引信是脉冲幅度调制与伪随机二相码复合调制引信，其工作原理框图如图1所示[8]。当回波信号满足固定的距离延迟、与本地延迟的伪码完全相关时，相关器输出信号幅值最大，经多普勒滤波、幅值检波等信号处理，产生启动信号，触发执行机构。图1中，Sr(t)为回波信号，S1(t)为带通滤波后信号，Sd(t)为混频后信号，PPAM为伪码调相脉冲多普勒引信伪随机码信号。

1.1 伪码调相脉冲多普勒引信发射信号

伪随机码p(t)可以表示为

i=0,1,…,∞;k=0,±1,±2,…,±∞

(1)

式中：P为伪随机码序列长度；Tm为伪随机码码元宽度；TR为伪随机码码元周期，TR=PTm；Ci={+1,-1}为双极性伪随机码序列。

伪随机码产生过程如图2所示，伪码调相脉冲多普勒引信伪随机码pPAM(t)可以表示为

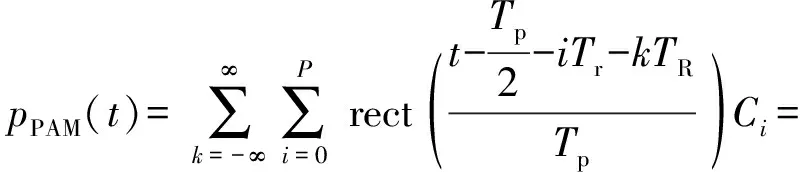
i=0,1,…,∞;k=0,±1,±2,…,±∞

(2)

伪码调相脉冲多普勒引信发射信号St(t)可以表示为

St(t)=AtpPAMcos(ω0t+φ0)

(3)

式中：At为射频脉冲幅度；ω0为载波角频率；t为时间；φ0为初始相位。

1.2 伪码调相脉冲多普勒引信回波信号处理

伪码调相脉冲多普勒引信的目标回波信号Sr(t)可表示为

Sr(t)=ArpPAM(t-τ(t))cos[(ω0+ωd)t]

(4)

式中：Ar为回波幅度；τ(t)为目标回波延迟时间；ωd为多普勒频率。

回波信号通过带通滤波器后进入混频器，与本振信号混频，经低通滤波后，通过距离门选通进入相关器，距离门选通脉冲信号是由脉冲发生器产生的脉冲信号作预定距离门延迟τA生成的。相关器的本地相关参考码是伪随机码序列作预定时间延迟τi而得的。其中τi=τA+kpTr,kp=0,1,…,P-1，进行相关检测得到相关输出信号ST(t)为

(5)

2 基于GAN的伪码调相脉冲多普勒引信干扰原理

干扰信号的重构精度是决定引信引导式干扰效果的主要因素之一。基于GAN的伪码调相脉冲多普勒引信干扰方法利用GAN对接收到的引信信号深度学习并由此重构出干扰信号。由于在低信噪比条件下重构出的干扰信号与引信信号具有非常高的相关度，避免了低信噪比条件下引导式干扰参数估计精度不足的问题，对于伪码调相脉冲多普勒引信而言，可以突破引信的二次相关检测，从而达到较为理想的干扰效果。

2.1 对接收到的引信信号预处理

2.1.1 时频分析

干扰接收机侦收到伪码调相脉冲多普勒引信信号后，经过滤波及去载频处理后得到中频信号，其时域波形如图3(a)所示，对中频信号进行频域分析得到其功率谱。频谱中大包络宽度为1/TR，每根谱线之间的距离为1/Tr。

以时间t0对中频信号进行剪裁，t0≥2TR，得到一定数量的波形片段，并对中频信号片段进行短时傅里叶变换(STFT)处理。STFT的数学表达式定义如下：

(6)

式中：f表示频率；sc(t)表示待分析的伪码调相脉冲多普勒引信中频信号；*表示复数共轭；γ(t)表示窗函数。为避免由于输入信号功率差异造成的特征量偏差，对得到的STFT时频图像进行幅值归一化处理，利用已训练好的降噪网络[19]对STFT数据进行降噪处理，该网络是一种前馈降噪卷积神经网络(DnCNN)，采用了用残差学习、加入批量归一化。将降噪后的STFT数据表示为图像如图3(b)所示。随后获取伪码调相脉冲多普勒引信中频信号的相位信息，同STFT一同传入GAN网络模型进行下一步处理。

2.1.2 信号降噪处理

利用深度残差神经网络的想法，文献[20]提出一种前馈降噪卷积神经网络的图像去噪方法，采用了用残差学习、加入批量归一化。不同于分类模型中的残差神经网络，去噪模型中纯净图片为xi，带噪声图片为yi，即网络的输入为yi=xi+n，其中n是残差图片，采用残差学习公式来训练残差映射F(y)≈n，去噪模型的优化目标为真实残差图片与网络输出之间的均方误差：

(7)

2.2 基于GAN的干扰信号重构

2.2.1 生成对抗网络

GAN基本结构如图4所示，主要包含两个部分：一是生成模型G，用来学习真实数据的真实分布特征，并生成新的数据，生成模型是以噪声或者随机序列作为输入得到第一代的生成数据；另一个是判别模型D，用来判断一个样本是真实样本还是生成样本，判别模型的输入数据包括真实数据和生成模型的生成数据，其本质上是一个二元分类器，将真实数据标记为1，生成数据标记为0。两个模型之间基于博弈论的思想通过对抗的方式来共同学习训练，直到生成与输入数据相关度极高的数据。

生成模型与判别模型都是由深度神经网络构成的，利用神经网络强大的拟合能力，在每一次交叉迭代训练中，修正生成模型参数，生成数据传入鉴别模型，计算判别模型的损失函数，经反向传播更新判别模型参数；随后固定判别模型参数，计算生成模型的损失函数，反向传播更新生成模型的参数，如此往复直至判别模型无法判断数据是来自输入数据还是生成数据，最终GAN逼近纳什均衡解。

真实样本模型可以表示为X，生成样本模型可以表示为Z，则有

X={x(1),x(2),…,x(m)}

Z={z(1),z(2),…,z(m)}

(8)

设真实数据的数据分布可以表示为pX(x)，生成模型的概率分布可以表示为pG(x)，生成模型参数为θ，且生成数据的数据分布为pG(z;θ)，模型训练过程中得到合适的θ使得pG(z;θ)无限接近pX(x)，最优生成模型参数值存在唯一解，且该唯一解满足pG(z)=pX(x)。GAN的目标函数表示为

V(G,D)=Ex～pX[log2D(x)]+Ez～pG[log2(1-D(z))]=

(9)

式中：Ex～pX、Ez～pG表示pX和pG两种分布的期望；D(x)表示x来自于真实数据分布而不是z的概率。

GAN网络的目的是最小化生成数据与真实数据之间的差异。

(10)

式中：arg表示自变量，判别模型就是对输入数据进行一个二分类，当数据进入判别模型时可以认为生成模型参数是固定的训练过程中最大化目标函数D*：

(11)

最优判别器满足：

(12)

判别模型的目的就是优化D：

Ex～pX[log2D(x)]+Ez～pG[log2(1-D(z))]

(13)

GAN网络是生成模型与鉴别模型之间相互博弈的过程，即最大值与最小值的问题。

Ez～pG[log2(1-D(z))]

(14)

2.2.2 基于GAN的干扰波形生成

基于GAN的干扰波型生成模型如图5所示。经预处理后的数据传入GAN模型中进行训练学习，经过生成模型与鉴别模型的博弈后生成与真实样本数据相似度极高的信号，以此信号为中频信号进行上变频，并对信号采用不同的延时后，由发射天线向干扰目标发射重构的干扰信号。

将生成信号作为中频信号上变频重构干扰信号sj为

sj=Ajzj(t)cos(2πfjt)

(15)

式中：Aj为重构干扰信号幅值；zj(t)为GAN生成的中频信号，可以近似表示为Zj(t)≈pPAM(t)；fj为干扰信号载频，令fj≈f0，f0为引信信号中心频率，可通过干扰机接收机侦测获得。

将重构的干扰信号进行延时，令延迟时间τ以一定的步长Δt不断变化，最大延时次数为N，从而可以确保模拟引信目标回波延时，使干扰信号可以通过引信的距离门检测，延时后由发射天线向目标引信发射干扰信号，引信接收到的干扰信号为

(16)

式中：A为引信接收到的干扰信号幅值。

干扰信号被引信接收后，首先通过一个中心频率为载频ω0的带通滤波器，用以滤除带外噪声。随后进入混频器，与本振信号U0(t)混频，经距离门及低通滤波后，获得输出信号为

(17)

式中：U0为引信载波幅度；fd为干扰信号产生的多普勒频率。

干扰信号经距离门及恒虚警放大限幅处理后进入相关器，并与引信本地相关参考码进行相关检测，得到相关输出信号为

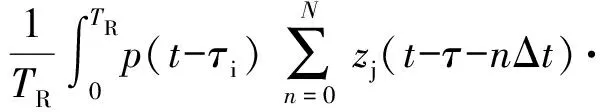
cos[2πfd(τ-nΔt)]dt

(18)

此时相关输出可以表示为

JGAN(t)=

(19)

3 仿真与讨论

根据图5所示干扰波形生成模型开展针对伪码调相脉冲多普勒引信的仿真实验。仿真工作参数设置如下：m序列伪码调相脉冲多普勒引信工作载频f0=100 MHz(原本10 GHz)；脉冲重复周期Tr=100 ns；脉冲宽度τ0=20 ns；脉冲占空比α=0.2；仿真采样率fs=1 GHz，m序列本原多项式为f(x)=x5+x2+1。

对m序列伪码调相脉冲多普勒引信信号作频谱分析如图6所示。

仿真实验前搭建生成对抗网络，结构如表1、表2所示。

表1 GAN生成模块结构

表2 GAN判别模块结构

根据上述参数搭建网络结构后，截取500个信号片段作STFT并将STFT的数据作为真实数据传入训练网络，采样点数为16 384个点，仿真环境为MATLAB软件，训练代数为1 000，生成模型学习率为0.001，鉴别模型学习率为0.001，衰减设定为0.5。将信噪比为-5 dB时真实数据传入模型并进行训练，在生成干扰波形时只需要消耗121 ms既可以生成全新的干扰波形。训练完成后生成的中频波形数据如图7所示。

得到伪随机码后对干扰信号进行重构，在GAN生成的干扰信号作用下得到引信相关器输出信号波形如图8所示，分别为GAN重构干扰信号作用下的引信相关器输出、启动信号及目标回波作用下的引信相关器输出。从图8中可以看出，在GAN重构干扰信号作用下，引信可以启动并且相关峰可以完全覆盖目标回波信号作用下引信相关器输出的相关峰，能够对引信产生有效的欺骗性干扰。

为验证GAN相比于传统引导式干扰的有效性，仿真采用方波调幅信号、正弦调幅信号对伪码调相脉冲多普勒引信实施干扰，不同干扰信号在相同干扰功率下对伪码调相脉冲多普勒引信的干扰效果如图9所示，并将其与图8中的效果进行对比。在相同干扰功率条件下，正弦波调幅和方波调幅干扰信号作用下引信相关器输出信号幅值很小，仿真中引信不能正常启动。而GAN网络重构干扰信号可以使引信正常启动，从而证明在相同干扰功率下，基于GAN的干扰波型重构方法对引信的干扰效果更佳。

将GAN重构方法和文献[8]的码元重构方法对伪码调相脉冲多普勒引信进行对比，文献采用3阶自相关函数法对m序列进行估计，以获取m序列的本原多项式，进而得到其完整码元重构干扰信号。文献定义3阶自相关函数为

(20)

式中：p、q为偏移量；l为离散时间序列。

在-5 dB环境下，利用基于GAN的引信引导式干扰方法重构信号后作用于伪码调相脉冲多普勒引信，引信相关及启动输出如图11所示，引信可以输出较宽的相关峰引信启动，表明-5 dB时基于GAN的伪码调相脉冲多普勒引信引导式干扰方法可以重构出与引信相关度很高的干扰信号，重构效果优于文献[8]的方法。

由上述仿真结果可知，基于GAN的伪码调相脉冲多普勒引信引导式干扰方法可以对伪码调相脉冲多普勒引信产生有效的干扰，且在低信噪比条件下效果优于传统引导式干扰及文献[8]提出的基于码元重构的伪码调相脉冲多普勒引信干扰方法，对引信码元的重构不受码元抽头数的限制。

4 实验验证

为验证前述结论，对伪码调相脉冲多普勒引信实施干扰。实验过程在微波暗室中进行，根据功率等效原则，近距离采用无线电引信干扰实验系统硬件平台模拟生成多种干扰信号，对伪码调相脉冲多普勒引信进行干扰。无线电引信干扰实验系统原理样机天线接收到引信信号后，首先经过下变频模块将引信信号由射频频段下变至中频频段。无线电引信干扰实验系统硬件系统样机在A/D 转换器后预留了观测接口，可以将该接口连接至示波器，从而直接观测到中频信号的时域波形，实验场景如图15所示。

观测并记录引信在不同干扰信号作用下的启动情况及启动最小干扰功率。图16所示为伪码调相脉冲多普勒引信频谱。图17为重构干扰信号作用下，伪码调相脉冲多普勒引信原理样机的启动情况。其中黄色波形表示引信相关器输出信号，蓝色波形表示引信启动信号。由图17可以看出，基于GAN重构的干扰信号可以产生明显的相关峰，使伪码调相脉冲多普勒引信启动。

实验过程中记录使引信启动的最小干扰功率，为保证实验结果的有效性，在确保能够成功干扰引信的基础上，选取了干扰效果较为稳定、成功率较高的干扰参数进行设置。表3给出了相同实验条件情况下，GAN重构干扰、典型压制式干扰以及数字射频存储(DRFM)干扰信号成功干扰引信所需的最小干扰功率。由表3可以看出，多种干扰信号中，基于GAN的干扰信号可以使伪码调相脉冲多普勒引信启动，且使引信启动的最小干扰功率最低，表明具有最优的干扰效果，实验结果与仿真结果一致。分析其原因可得：引信发射信号在传播过程中会伴随信噪比的损失，此时DRFM存储并转发的引信信号已经失真，其转发信号与引信发射信号相关性下降；而GAN重构信号能够根据训练样本与对抗生成网络，重构出与引信信号相关性较高的干扰信号，使引信对其信干比处理增益最小，因此能够以较小的功率成功干扰引信。