装备维修器材预储点选址与预置运输配送组合优化方法

曹军海，张闯，李延通，郭一鸣，郭庆义

(1.陆军装甲兵学院 装备保障与再制造系，北京 100072；2.大连海事大学 航运经济与管理学院，辽宁 大连 116026；3.65316部队，辽宁 大连 116300)

0 引言

装备维修器材的预储预置，是保障作战部队在战争初期快速获得器材供应的重要手段，是提高装备维修器材保障效率和部队持续战斗力的关键之一。美军在海湾战争、伊拉克战争等21世纪以来的几次局部战争中，通过海上、陆上等预储预置力量，实现了装备和物资的快速部署，促进了部队战斗力的快速生成，对后续作战行动起到了促进作用[1]。当前，我国陆军正在进行深刻改革，从区域防卫型向全域机动型转变。面对当前我周边复杂备战形势，有必要在主要战略方向预先配置一定规模的装备维修器材，避免保障任务初期出现保障难、保障慢的问题，提高战时部队部署效率，快速形成战斗力和保障力。

针对战时预置储备问题，一些学者已经进行了研究。林勇等[2]对美国陆军预置储备情况进行系统梳理，并结合我国陆军实际提出了建设启示。李守耕等[3]分别对边境地区、岛礁、海外基地和海上舰船4种战备物资预置方式进行研究，并提出可行方案。王耀等[4]针对岛屿、边境和海外等3种作战环境下后勤战备物资预置储备进行总体设计。在战时军事物流的文献中，张巍等[5]研究了战时前沿补给基地的选址问题。王申坪等[6]针对战时装备仓库选址问题，提出了基于两阶段的广义最大覆盖模型，并针对某次演习任务中装备仓库的选址进行了仿真分析。吕游等[7]研究了战时物流配送路径规划问题，姜大立等[8]对战时不确定环境下的军事运输动态路径规划问题进行了研究。

从当前已有文献来看，一方面，对装备物资预置储备的文献大多集中于总体设计和方案研究，少有对主要战略方向预储点选择和战前装备物资快速预置等问题的优化方法研究。另一方面，战时军事物流的文献中，大多研究装备物资仓库或基地的选址问题，或运输配送问题，而很少将二者作为一个问题同时考虑。事实上，设施(仓库)选址和基于设施位置的运输配送二者紧密相关，设施选址是运输配送的前提和基础，后期运输配送是设施选址的目的和后续。传统的优化方法将二者作为独立问题分别研究，首先确定设施选址方案，当预置任务开始时，基于前期选址确定的设施位置，进行需求分配和运输保障。这种模式无法保证其方案的全局最优，与信息化战争中对装备器材保障的精确、高效等需求不相适应。为了获得全局最优的保障方案，需要将二者进行有效融合，形成一类复杂的组合优化问题——选址调度问题(ScheLoc)。

ScheLoc问题是近年来广受关注的一类组合优化问题，最早由Hennes等[9]于2002年提出。ScheLoc问题有效融合了设施选址和机器调度两类经典运筹优化问题，其决策环节主要包括设施的选址、设施和需求的分配以及各设施对所分配需求的服务次序等。按照设施数量，ScheLoc问题分为单机ScheLoc问题(即只有一个设施)[10-11]和并行机ScheLoc问题[12-13]；按照选址类型可分为平面ScheLoc问题(即在一定范围内任意位置选址)[14]和离散ScheLoc问题(在指定待选位置集内选址)[15]。近年来，一些学者还就不确定环境下的ScheLoc问题进行了研究，形成了一些有意义的研究成果[16-17]。在现实生产生活中，ScheLoc问题被广泛应用在港口管理[18]、矿石开采[19]、物流配送中心规划[20]等问题的优化中。目前ScheLoc问题在军事中的研究较少，Wesolkowski等[21]针对军事训练设施的选址和参训部队的训练规划进行了研究，以多种成本目标及总训练时间的最小化为目标，构建了双目标模型，并利用NSGA-Ⅱ算法进行了求解。值得注意的是，本文仅研究训练设施选址和参训部队分配两阶段问题，未对各部队训练次序进行规划。而本文所研究的预储点选址与预置运输配送组合优化，将预置运输配送次序纳入研究范围，形成更完整的优化方案。

因此，本文针对装备维修器材预储预置问题，将预储点选址和战前装备维修器材预置融合为ScheLoc组合优化问题，决策环节包括装备维修器材预储点的选择、器材使用部队(即需求点)与预储点的分配关系，以及各预储点进行器材预置时的保障次序，属于离散并行机ScheLoc问题。通过考虑预储点开设成本、运输成本以及保障延误惩罚成本等目标，构建混合整数规划模型，并开发高效的求解算法，获得全局最优的器材预储预置方案，保证在作战任务开始前快速完成装备维修器材的部署，保障部队作战任务的开展。

1 问题描述

本文考虑在某战略方向上，拟于适宜进行装备维修器材预储的待选位置集合中(通常选用现有装备维修器材仓库或其他已有设施场地)，选择并设立若干预储点进行装备维修器材的预先储存，并在战争开始前，按照部队部署情况及时将器材预置至指定位置。具体过程可描述如下：

考虑某次实战化演练中，保障部门拟在经勘查评估确定的l个备选位置中，最多选择开发m个预储点，记预储点备选位置集合K={1,2,…,l}为预储点备选位置集合，要在其中选择开设m个预储点。对位置k(k∈K)，其坐标为(Xk,Yk)，开设固定成本为ck，器材存储上限为Qk，部署运输车队编组集合为Bk={1,2,…,b,…,|Bk|}，负责器材的运输和预置。车队编组b以整车队形式独立执行任务，不与其他编组进行车辆借调。假设本地域即将部署n个作战部队，构成部队集合为J={1,2,…,n}，每个部队j(j∈J)的坐标表示为(Xj,Yj)，根据作战计划，其对装备维修器材的需求量为pj。在预置任务开始前，需要解决部队器材需求和预储点的分配，以及预储点对各部队预置器材的先后次序。当部队j的需求分配至预储点k时，由该预储点的车队b将器材从预储点k运送至部队j的部署位置，完成预置后立刻返回，执行下一次运送任务。假设每个车队单次只运送一个部队的器材，且该部队的需求量能够被车队一次性保障完毕，其单程运送时间rjk和运输成本ejk与部队j与预储点k之间的距离gjk有关，表示为rjk=gjk/s，ejk=egjk，其中s和e分别表示行车速度和单位距离运输成本，本文均假设为定值。由于不同部队担负的任务不同，其对于器材需求的迫切程度也不同，假设部队j的期望到达时间为dj。若在该期限内未能到达，将产生延误时间，同时将影响部队后续任务的开展，因此必须承担一定的延误惩罚成本。记Cj为部队j的器材到达预定地域的时间，即保障完成时间，Tj为延误时间，则Tj=max(Cj-dj,0)。定义qj为部队j的单位时间延误惩罚成本。本文的决策内容包括预储点的选择、部队与预储点的分配关系建立，以及预储点运送器材的先后顺序。为兼顾军事效益与经济效益，本文优化目标为预储点总固定费用、总运输成本以及总延误惩罚成本的加权和最小，三者的权重分别表示为θ1、θ2、θ3。

2 模型构建

根据第1节的问题描述，为构造混合整数规划模型，首先对问题进行如下假设：

1)预储点固定开设成本可知；

2)战时装备维修器材采用基数化存储，器材量单位为基数，且不区分器材品种；

3)战时装备维修器材采用集装化运输和机械化装卸，其装载、卸载时间忽略不计。

同时，定义如下决策变量：

wk=1，表示备选点k被选为预储点，否则为0；

vjkb=1，表示部队j由预储点k的车队b保障，否则为0；

xij=1，表示部队j的保障次序在部队i之后(无需相邻)，否则为0。

由以上问题假设及变量定义，构建混合整数规划模型，记为P，其表示方式如下：

(1)

s.t.

(2)

(3)

(4)

(5)

(6)

Cj≥Ci+rik+rjk-L(3-xij-vjkb-vikb)

(7)

Ci≥Cj+rik+rjk-L(2+xij-vjkb-vikb)

(8)

Tj≥Cj-dj

(9)

Tj≥0

(10)

wk∈{0,1}

(11)

vjkb∈{0,1}

(12)

xij∈{0,1}

(13)

3 算法设计

本文问题是设施选址和并行机调度两类问题的组合优化，设施选址和并行机调度问题已被证明均属于NP-难问题[22-23]，因此本文研究的问题也属于NP-难问题。组合优化使得问题能够获得全局最优解的同时，也极大地增加了模型的复杂度和求解难度，需要设计高效算法进行求解。针对该问题，本文首先生成一种基于逻辑的Benders分解(LBBD)算法，该算法是一种精确算法，在求解复杂的组合优化问题时性能较好。同时，为了对比组合优化与传统优化方法的表现，还构造了一种序贯式优化(SH)算法。以下对两种算法的原理和流程分别进行介绍。

3.1 基于逻辑的Benders分解

LBBD算法是一种基于松弛分解、迭代切割的精确算法。首先，经典Benders分解算法由Benders于1962年提出[24]，其基本原理为：将原问题中的复杂变量固定松弛，分解为一个主问题和一个子问题，主问题为原问题的松弛问题，其计算结果构成原问题的下界(LB)，主问题求解完成后将解传至子问题，求解形成原问题的上界(UB)，子问题求解后生成Benders切割，并添加至下一迭代的主问题中，以提高问题下界。由此反复迭代，直至求得最优解(LB=UB)，或到达最大计算时限。经典Benders分解算法中，子问题形式被限定为线性规划问题，限制了该算法的应用范围。21世纪初，Hooker等[25]将经典Benders分解算法扩展，形成基于逻辑的Benders分解(LBBD)算法，其子问题可为任意优化问题。LBBD算法自提出以来，在组合优化问题的求解中展现出了显著优势，在机器调度[26]、路径规划[27]以及医院手术室调度[28]等问题中得到了成功应用。

对模型P，首先将目标函数中保障延误惩罚成本松弛，形成的主问题主要解决预储点选址和部队器材需求与预储点的分配两个决策问题，当以上决策变量求解并固定后，子问题则变为求解一系列单机调度问题，以在各车队上最小化完成所有保障任务出现的延误惩罚成本。随后，子问题生成Benders切割，并添加至下一迭代中的主问题。值得注意的是，Benders切割可分为可行性切割和最优性切割，但在本文问题中，子问题求解时总存在可行解，因此本文所生成的Benders切割均为最优性切割。下面对主问题、子问题以及Benders切割的表示进行详细描述。

3.1.1 主问题

为表示主问题，定义ψ为目标函数中总延误惩罚成本的下界，将该部分以及对应的器材运送次序决策环节松弛，使得主问题成为研究预储点选址、部队与预储点分配的松弛问题，松弛后的主问题表示为

(14)

s.t.

(2)式～(5)式，(11)式，(12)式，及

CUTS

(15)

此时，目标函数(14)式表示预储点固定成本、运输成本及总延误惩罚成本下界的加权和。约束(15)式的CUTS即表示迭代过程中产生并添加至主问题的Benders切割。此时，由于对问题进行了松弛，ψ下界较差，使得主问题质量较差，需要根据问题结构特点提出有效不等式，对主问题进行加强。

3.1.2 有效不等式

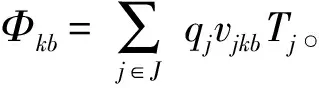
(16)

(17)

(18)

(19)

Φkb≥0

(20)

Tj≥0

(21)

(16)式表明总延误惩罚成本不小于所有预储点的车队的延误惩罚成本之和；(17)式表示总延误惩罚成本不小于所有部队各自延误惩罚成本之和；(18)式表示各运输车队的延误惩罚成本，不低于最小单位延误时间惩罚成本与最小延误时间的乘积，其中，最小延误时间以车队保障最后一个部队的最短用时与最大期望到达时间之间的差；(19)式表示部队j的延误时间不小于该部队与所所分配的预置点之间的距离与期望到达时间的差，即部队j为车队的第一个保障对象。

3.1.3 子问题

当主问题求解完毕后，预储点选址变量wk、分配变量vjkb等的值得以确定，此时子问题则变为求解一系列单机调度问题，即在各预储点位置上被分配有器材预置任务的车队，其保障次序的确定，目标为最小化该车队产生的总保障延误惩罚成本。定义集合Jkb为预储点k中车队b所承担的部队器材预置任务，即Jkb={j|vjkb=1,∀j∈J}。定义变量zij表示部队i和j的保障次序相邻，且i在j之前。则对预储点k中车队b的子问题可表示为

(22)

s.t.

zij+zji≤1

(23)

Cj≥Ci+rik+rjk-L(1-zij)

(24)

Cj≥rjk

(25)

Tj≥Cj-dj

(26)

Tj≥0

(27)

zij∈{0,1}

(28)

目标函数(22)式表示在预储点k中车队b处的总延误惩罚成本最小化；约束(23)式表示两部队i和j的保障次序关系，即部队i不可能同时既是部队j的前一保障对象又是部队j的后一保障对象；约束(24)式～(27)式与对应前述约束(7)式～(10)式；约束(28)式为变量zij的域。

根据Graham等[29]提出的三段分类法，此处所描述的子问题可表示为1‖∑qjTj。该问题已经被证明为强NP难问题。当前对1‖∑qjTj问题的求解已有较多文献，其中精确算法包括分支定界、动态规划、列生成等。经过前期试验，由Tanaka等[30]提出的基于动态规划的精确方法具有良好的性能。该方法基于提出的Ibaraki等[31]提出的SSPD算法，通过多种改进策略，解决了SSPD算法内存使用大、计算效率低等问题，经过数值实验，这种基于动态规划的方法能够在合理时间内求解工件数量(即本文中的部队数)达300的无空闲时间的单机调度加权延误时间最小化问题。因此，本文应用Tanaka等的动态规划方法对子问题进行求解，并基于子问题的结果生成Benders切割。

3.1.4 Benders切割

(29)

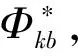
3.2 传统序贯式算法

为比较组合优化方法与传统优化方法的性能，本节构造一种序贯式优化方法(记作SH)，通过两个阶段依次对问题进行求解，即：先以预储点开设固定成本和运输成本最小化为目标，求解预储点选址和部队需求分配问题。第一阶段完成后，第二阶段转化为针对承担预置任务的各运输车队单机调度问题，优化目标为总延误惩罚成本最小化。为了保证算法的性能，两阶段分别使用精确方法进行求解。下面分别对各阶段的求解方法进行详细描述。

3.2.1 第一阶段

本阶段以预储点固定成本和运输成本最小化为目标，构造MILP模型如下：

(30)

s.t.

(2)式～(5)式，(11)式，(12)式

3.2.2 第二阶段

第一阶段求解完成后，选址变量wk和分配变量vjkb得以固定，此时第二阶段转化为一系列求最小延误惩罚成本的单机调度问题。该问题与3.1.3节类似，为提高后期数值实验计算结果对比的可信度，本阶段采用与4.3节相同的求解方法，即Tanaka等[30]的基于动态规划的精确求解方法。

4 数值实验

为评估本文所提出的模型和算法的性能，随机生成160个算例对模型P及算法LBBD和SH进行测试实验，首先对算例的生成规则进行简要介绍，随后对实验结果进行汇总和分析。

4.1 算例生成

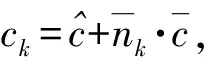
本文所提出的模型P、算法LBBD和SH，均通过C++链接求解器Cplex12.10编程实现，其中模型P利用CPLEX求解器直接求解时，其内核算法为分支切割算法。每个算例的求解时限设置为600 s。运行环境为Intel Xeon CPU E5-2690 v3，2.60 GHz，32 GB RAM。为更好地对计算结果进行分析，将该部分算例分为3组，分别是常规算例组(20≤n≤60)、大算例组(80≤n≤120)和超大算例组(140≤n≤200)。下面分别对各组算例的计算结果进行分析。

4.2 常规算例组结果

常规算例组的计算结果如表1所示，表格中前4列表示算例相关参数，分别为部队数n，待选位置数l，预储点数m，以及各预置点运输车队数b。中间3列表示各模型和算法的求解质量，用上界UB和下界LB的差值百分比Gap(%)度量，其计算方式可表示为

(31)

值得注意的是，SH是一种两阶段序贯式优化方法，无法准确获得整个问题的有效下界，因此其下界采用模型P和算法LBBD所生成的最好下界，并利用其自身上界求得算法SH的Gap值。由于本节所生成的算例考虑TF和R值不同，每种规模的算例共有4个具有不同期望到达时间的算例，因此表1中各算例数值为4个算例的平均值。最后一行括号内数字代表该组取得最优解(Gap=0)的算例的数量。表格右侧3列为各算例的计算时间。

从表1中可以看出，在常规算例组的实验中，本文所提出的模型P和算法LBBD均取得了良好的求解效果，LBBD算法获得了最多得最优解，为28个，模型P得到27个最优解，略低于LBBD，而算法SH仅有2个最优解。LBBD算法的平均Gap值为3.10%，在三者中表现最好，模型P的Gap值为3.71%，高于LBBD算法，但明显好于SH算法的25.69%。从求解效率上看，LBBD同样表现最好，其平均计算时间为262.77 s，模型P的平均计算时间为279.99 s。SH由于采用序贯式优化方法，其问题复杂度低，平均求解时间不到1 s，但同时解的质量较差。

从表1中还可以观察到，对模型P和算法LBBD，总体上看，其运输车队数量越多，解的质量越好。从表1中可以统计发现：在该组算例中，当车队数量为3时，模型P平均Gap为4.53%，算法LBBD的平均Gap值为3.71%；当车队数量为5时，二者分别降为2.95%和2.49%，降幅均超过30%。其可能的原因为：在同等算例规模下，当车队数量较少时，每个车队将分配更多需求，由于以加权延误时间最小化为目标的单机调度问题为NP难问题，其求解复杂度高，可能造成求解质量相对较低。

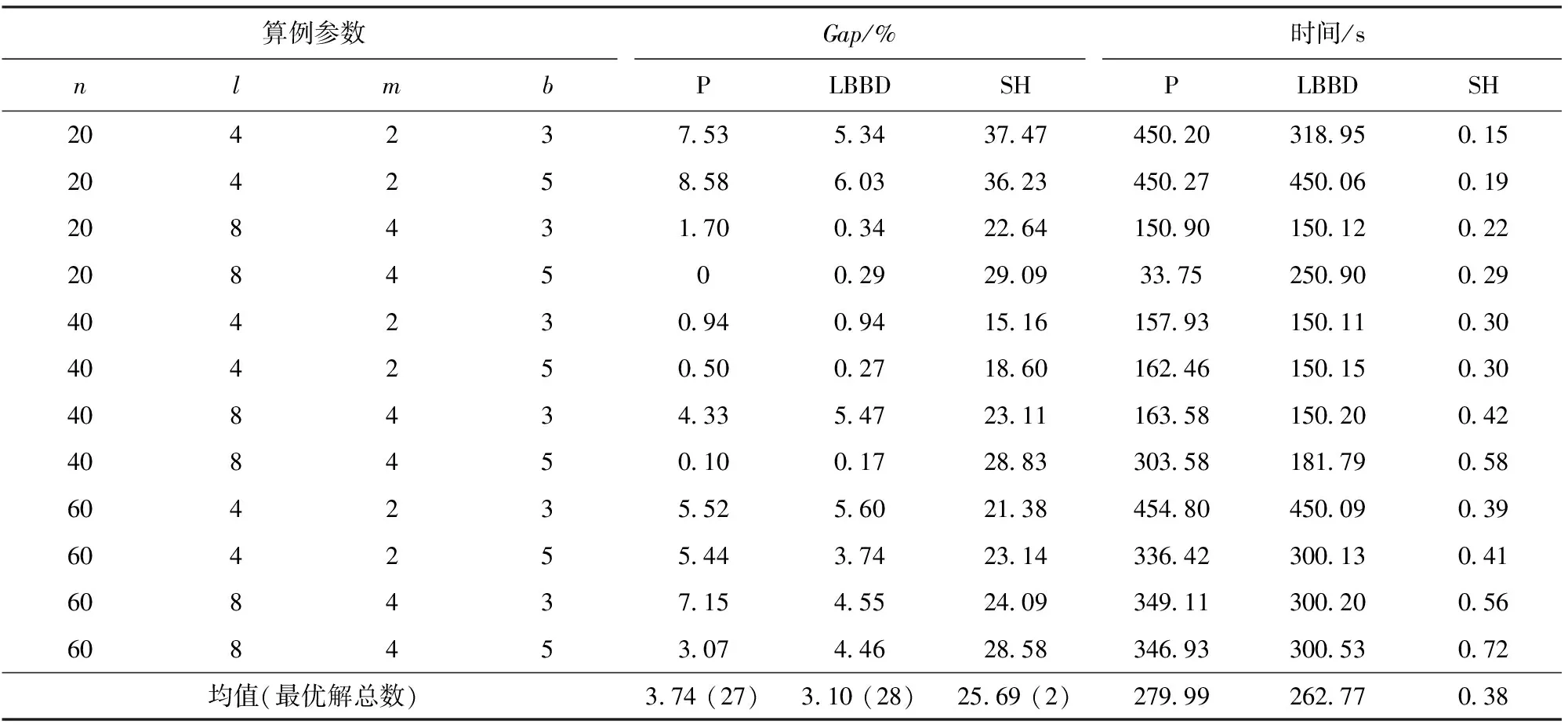
表1 常规算例组计算结果

4.3 大算例组结果

大算例组为部队数量为80～120的算例，计算结果如表2所示。从表2中可以看出，大算例组的求解难度相对于常规算例组有所增大，模型P的表现出现明显下降。从求解质量上看，模型P共取得15个最优解，其平均Gap值为19.78%，平均用时为493.27 s。LBBD算法得到27个最优解，其平均Gap为5.32%，平均计算时间为263.04 s，明显优于模型P。SH的计算效率仍最高，平均计算时间在 1 s 以内，但其求解质量相对较差，其平均Gap高达21.11%，共获得12个最优解。

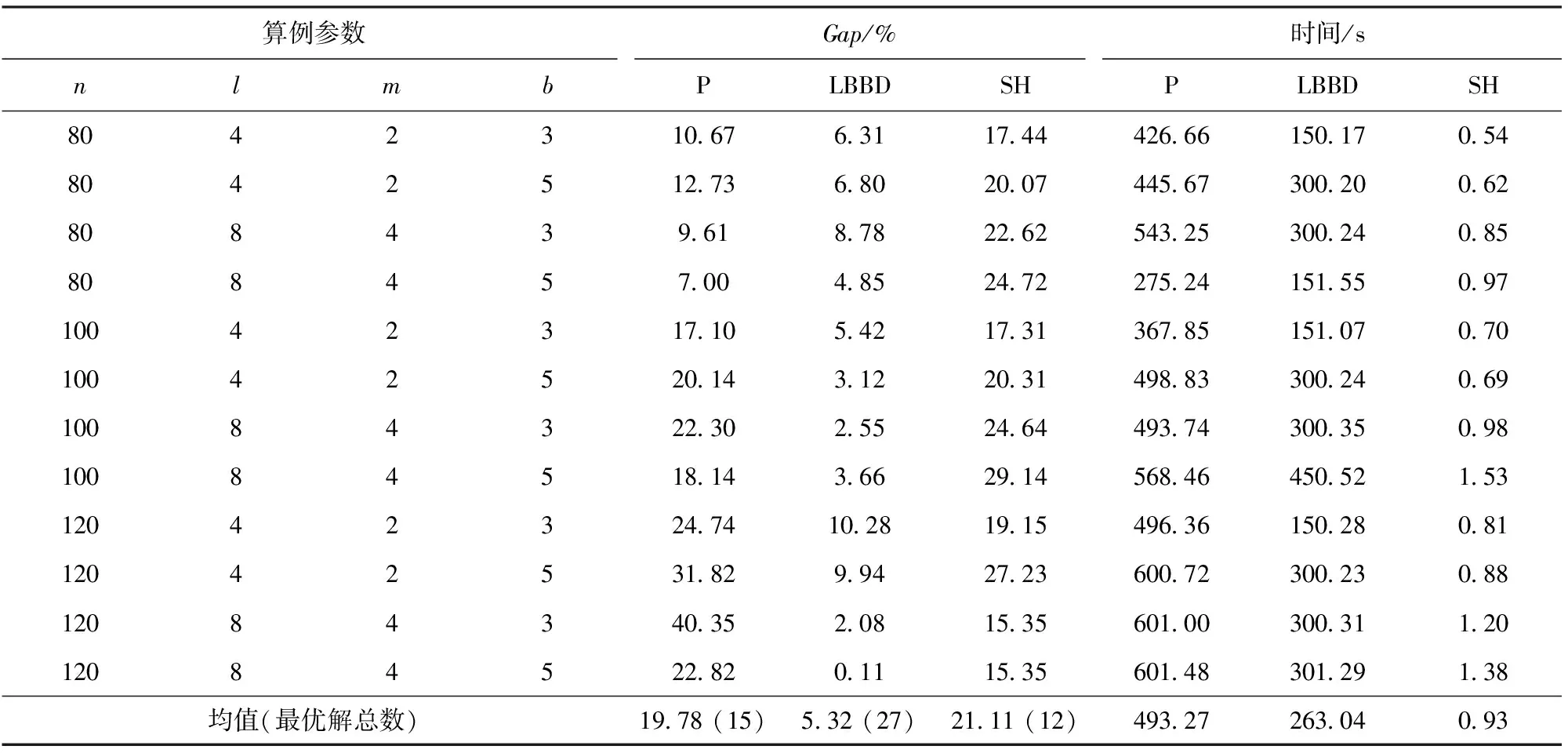
表2 大算例组计算结果

4.4 超大算例组结果

为进一步评价和探索模型P及算法LBBD、SH的性能，本文对超大规模算例进行了实验，该组64个算例中，部队数n={140,160,…,200}。即：决策者要对某战略方向上最高达200个装备维修器材预置任务进行预储点选择和预置方案决策，计算结果如表3所示。

针对表3中的计算结果，从求解质量上看，算法LBBD的表现相比模型P和算法SH具有明显优势。在64个算例中，LBBD共求得34个最优解，其平均Gap值为8.00%。SH获得18个最优解，其平均Gap值为23.11%。模型P随着算例规模的增加，表现显著下降，在超大规模算例中性能最差，仅在n=140的算例中获得2个最优解，平均Gap值达到80.21%，远高于算法LBBD和SH。在n=180的算例中，模型P的平均Gap值均在85%以上，而当n=200时，平均Gap值均大于98%，此时模型P已基本失去优化求解能力。从计算时间上看，模型P平均计算时间为596.39 s，接近计算时限600 s，算法LBBD的平均计算时间为289.83 s，相比表2中的263.04 s较稳定，算法SH的平均计算时间只有1.4 s。

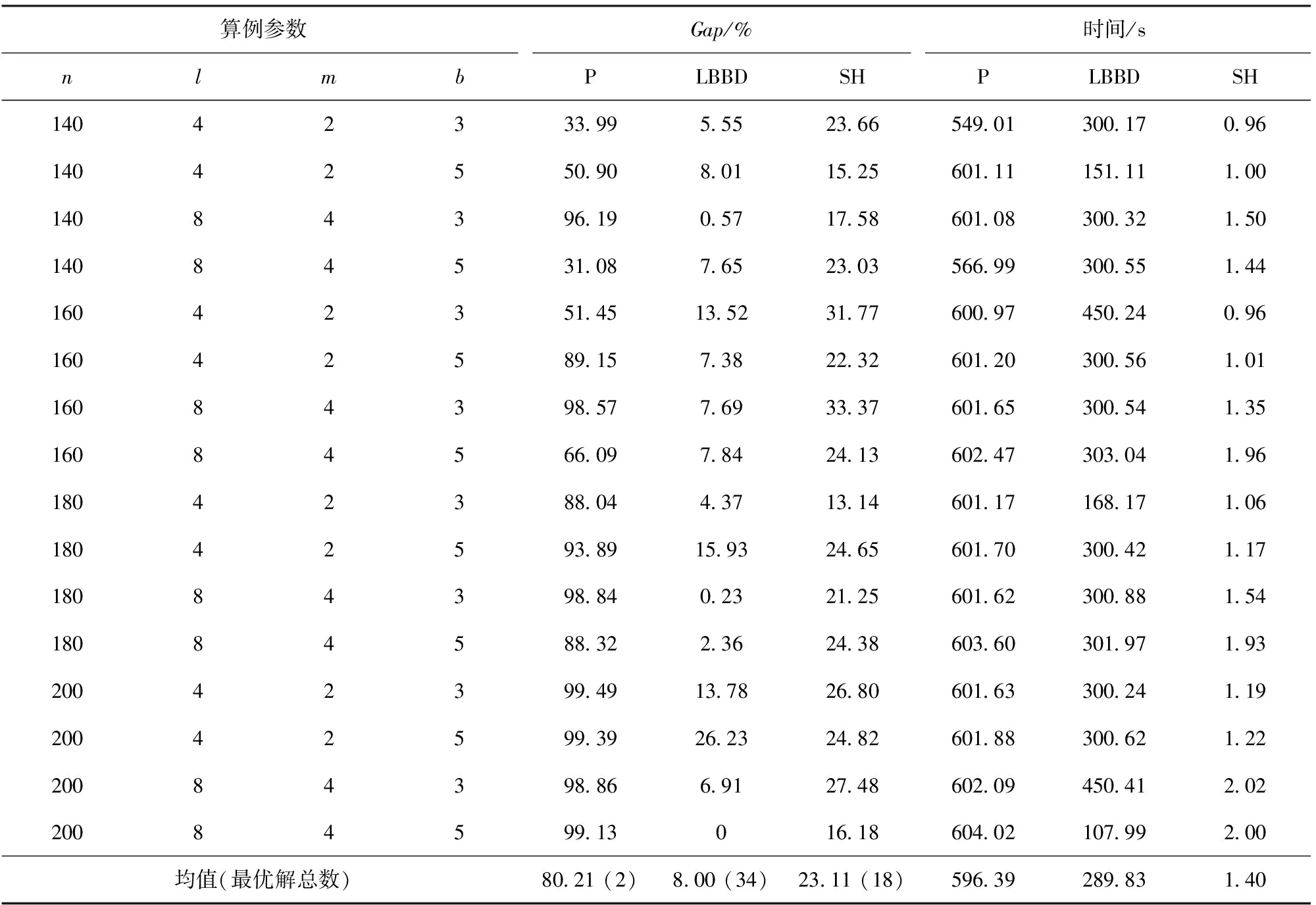
表3 超大算例组计算结果

从3组算例的计算结果来看，算法LBBD在3种方法中表现最好。在160个算例中，LBBD共求得89个最优解，总平均Gap值为5.73%；算法SH获得32个最优解，其平均Gap值为23.29%；模型P获得44个最优解，平均Gap值为39.14%。当算例规模增大时，模型P的性能下降明显，在48个常规算例中，模型P求得27个最优解，平均Gap值为3.74%，而在64个超大算例中，两项数据分别变为2个和80.21%，说明在本文所研究的组合优化问题具有较高的复杂性。而算法LBBD保持了良好的求解稳定性，3组算例的平均Gap值分别为3.10%，5.32%和8.00%。在组合优化LBBD算法与序贯式优化方法SH算法的比较中，LBBD的求解质量显著高于SH，证明了组合优化方法在获得更高质量解方面的优势。

同时，分析表1～表3的结果发现，算法SH求得的最优解数量随着算例规模的增大而增加，经过分析发现，其原因主要与期望到达时间有关。因此，接下来对不同期望达到时间对问题求解的影响进行分析。

4.5 期望到达时间的影响

4.1节详细介绍了期望到达时间的生成方法，其中参数TF的大小影响整体的松紧程度，即TF值越大，整体期望达到时间越短，表明战争的突发性越强，需要在最短时间内完成器材预置；反之，整体期望达到时间越长，体现战争准备时间较充裕。参数R的值反映了不同部队对器材到达时间需求的差异性。R值越小，说明期望到达时间分布越集中，反之则越分散。本节对不同TF和R值组合下各模型和算法的表现进行分析，其结果如表4所示。值得注意的是，表4中每个结果均为40个算例结果的平均值，括号内为取得的最优解数量。

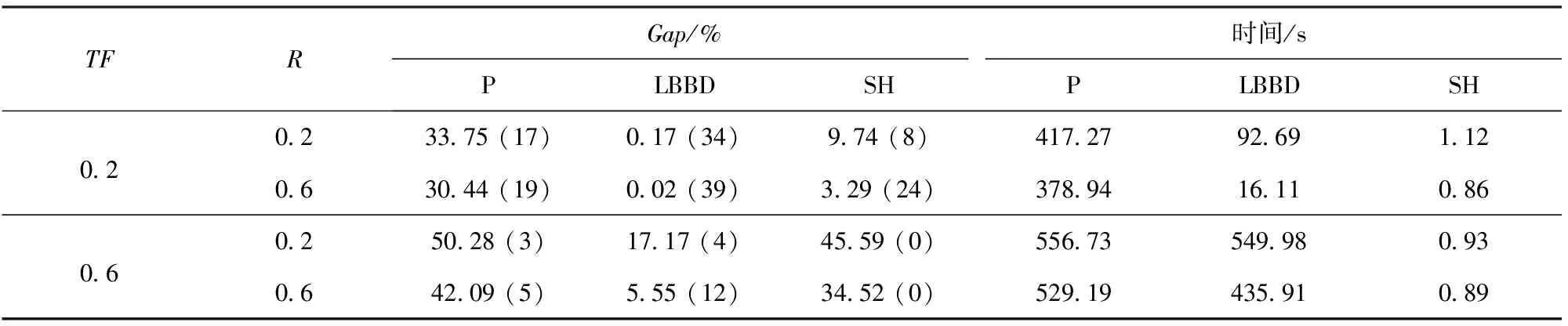
表4 期望到达时间的影响

从表4的结果来看，不同TF和R值的组合对各模型和算法的求解具有显著影响。当(TF,R)=(0.2,0.6)时，表明整体期望到达时间较长，且分布较散，即：战争准备时间充足，各部队需求紧迫性差异大，此时问题复杂度较低，因此各模型和算法表现较好。以算法LBBD为例，在该组的40个算例中，LBBD取得39个最优解，平均Gap仅为0.02%，平均计算时间16.11 s，明显好于在其他(TF,R)组合中的表现。在该组中，算法SH获得24个最优解。由于当算例规模增大时，运输成本在目标函数中的比重上升，而该组延误惩罚成本较低，使得SH获得最优解的能力上升。因此，在表1～表3中，算例规模越大，算法SH获得的最优解数量越多。当(TF,R)=(0.6,0.2)时，表明战争准备时间较短，且各部队均面临紧迫的装备维修器材需求，此时问题求解难度最大。在各模型和算法中，LBBD算法表现最好，其平均Gap值为17.17%，明显好于模型P的50.28%及算法SH的45.59%。

从动态角度看，当TF值不变，R值由0.2增加至0.6时，表示各部队期望到达时间由集中变得分散，此时各模型和算法获得的最优解数量增加，平均Gap值降低，平均计算时间缩短。以算法LBBD为例，TF=0.2情况下，当R值由0.2变为0.6时，平均Gap值由0.17%降为0.02%，最优解数量由34变为39，平均计算时间由92.69 s缩短为16.11 s。当R值不变、TF值增大时，表示整体期望到达时间缩短，从表4的数据来看，问题求解难度大大增加，各模型和算法的表现均有下降。以模型P为例，R=0.2情况下，当TF值由0.2变为0.6时，平均Gap值由33.75%增至50.28%，最优解数量由17变为3，平均计算时间由417.27 s变为556.73 s。同时，从表4中结果可以总结发现，TF值变化所产生的影响远大于R值变化的影响，即：战争准备时间是否充足，是影响装备维修器材预储预置决策难度的主要因素。同时，决策者也应关注不同部队需求紧迫性之间的差异。

5 结论

本文研究了装备维修器材预储点选址与预置运输及配送优化方法，将预储点选址与战前器材预置融合为一类选址调度组合优化问题，构建以预储点固定成本、运输成本与保障延误惩罚成本最小化为目标的混合整数线性规划模型，设计了一种基于逻辑的Benders分解算法(LBBD)和一种序贯式优化方法SH，并基于160个随机算例进行了数值实验。得出以下主要结论：

1)该问题属于NP难问题，对模型P直接求解时，其表现随问题规模增加而显著下降，需要开发高效的求解算法。

2)提出的LBBD算法获得的最优解数量最多，求解质量最好。序贯式算法SH采用两阶段分别精确求解的优化方法，其求解效率高，但求解质量低。LBBD与SH算法的对比实验证明组合优化方法在获得更高质量解方面具有优越性。

3)战争准备时间以及不同部队期望到达时间的差异性对问题的求解具有重要影响，进一步表明了装备维修器材预储预置的总要性。

下一步可针对考虑战时不确定性和中断风险的装备维修器材供应保障优化方法进行研究。