深水爆炸二次压力波超压峰值的工程模型

2022-12-01王树山梁策高源桂秋阳刘建湖盛振新

兵工学报 2022年10期

王树山，梁策，高源，桂秋阳，刘建湖，盛振新

(1.北京理工大学爆炸科学与技术国家重点实验室，北京 100081；2.中国船舶科学研究中心，江苏无锡 214082)

0 引言

炸药水下爆炸形成爆炸冲击波和气泡脉动，气泡脉动辐射脉动压力波[1-2]。冲击波后的首个脉动压力波称为二次压力波，尽管其超压峰值只有冲击波的10%～20%，但其能量接近冲击波的50%，冲量水平与冲击波相当[3-4]，因此成为一种备受关注的重要毁伤载荷。在水深变化条件下的水下爆炸中，气泡能随爆炸深度的增加而增大[5-6]，水深对气泡脉动和二次压力波的影响不可忽略，因此研究水深对二次压力波的影响并获得适用于数千米水深范围内深水爆炸二次压力波超压峰值的工程计算模型，非常具有理论意义和工程应用价值。本文基于此开展水深对于二次压力波超压峰值影响的研究。

相似理论和量纲分析是水下爆炸相关问题研究的基本方法和手段之一，早在1919年，Hilliar就提出了基于量纲分析和爆炸相似律的水下爆炸冲击波压力计算公式[7]，1948年，Cole[3]给出了典型炸药水下爆炸冲击波和二次压力波的爆炸相似律经验公式，被视为经典并沿用至今。然而这些公式均未考虑水深的影响。在此之后，Keil[8]、Stiepanow等[9]、Henrych[10]、Geers等[11]以及周霖等[12]从各自的研究出发，分别给出了有代表性的水下爆炸冲击波相似律模型。毋庸置疑，以爆炸相似律为基础的工程模型作为定量计算与分析水下爆炸参数的基本方法和手段，已得到广泛认同和普遍应用[13-14]。

针对二次压力波特别是深水爆炸二次压力波的专题研究相对比较鲜见，早期具有代表性的工作可追溯到1950年前后，Arons[15]提出了考虑水深影响的二次压力波理论分析方法，Bernard[16]给出了500 ft(152.4 m)水深以内的二次压力波超压峰值与水深的函数关系。1967年，美国海军军械实验室[17](USNOL)进行了深水爆炸试验，基于爆炸相似律通过试验数据拟合，得到了深水爆炸二次压力波峰值压力的经验公式。该公式依水深采用2阶分段函数形式，其中第1段(500～4 000 ft/152.4～1 219.2 m)函数不含水深变量即与水深无关，这明显源于对有限试验数据的误解和机械处理，有悖于物理常识和逻辑。2012年，姚熊亮等[18]给出了一种含水深变量的二次压力波峰值压力计算公式，能够直观反映峰值压力随水深的连续变化，但不符合严格意义上的爆炸相似律，欠缺理论和试验依据。本文采用有试验依据的数值仿真研究方法，分析水深对二次压力波超压峰值的影响，以爆炸相似律为基础并利用仿真数据，建立物理含义明确的深水爆炸二次压力波超压峰值的工程模型。

1 数值模型

1.1 网格模型和边界条件

基于AUTODYN数值模拟软件建立的一维楔形网格模型如图1所示，水域半径设定为100 m。装药为球形TNT炸药，质量和尺寸可调整，起爆点设置在装药中心。为保证计算精度和提高计算效率，采取渐变网格的划分方法，网格划分密度由爆心处1 mm/格渐变为最远处的10 mm/格。边界条件选用默认的固壁面(rigid)边界条件，这样虽然存在边界处的冲击波反射，但由于所建水域足够大，能够保证本文所有算例反射冲击波到达距爆心最远观测点的时间均大于二次压传播至该观测点的时间，因此各观测点所采集的二次压力波数据不受反射冲击波的影响。

1.2 炸药状态方程与参数

炸药状态方程选择JWL状态方程，即

(1)

式中：p为爆轰产物的压力；E0为单位体积内能；A、B、R1、R2、ω为常数，其值通常通过炸药圆筒实验研究；V为相对体积。

所研究的TNT炸药参数及JWL状态方程参数，直接取AUTODYN软件材料库中TNT-2相关参数，如表1所示。

表1 TNT炸药参数及JWL状态方程参数

1.3 水状态方程与参数

水介质采用多项式状态方程，压缩(μ>0，μ=ρ/ρ0-1，ρ为水介质密度，ρ0为常温常压下水的密度，ρ0=1.0 g/cm3)状态和拉伸(μ<0)状态的形式分别为

p=A1μ+A2μ2+A3μ3+(B0+B1μ)ρ0e

(2)

p=T1μ+T2μ2+B0ρ0e

(3)

式中：p为水介质压力；e为水介质比内能，e=(p0+ρ0gH)/B0，p0为大气压，g为重力加速度，H为水深,B0为常数；A1、A2、A3、T1、T2、B1均为常数。这样，就可以根据水深来调节水介质比内能e，从而实现不同水深情况下的计算。状态方程的主要参数选取AUTODYN材料库中的默认参数，如表2所示。

表2 水介质多项式状态方程参数

2 模型校验

利用模拟深水爆炸罐试验数据与对应工况的模型计算结果进行对比分析，为数值模型的正确合理性以及仿真结果的准确有效性提供试验依据。模拟深水爆炸罐试验原理为：首先向罐内注水并达到预定水量，然后保持密闭并通过空压机对罐内空气加压，通过调整和控制罐内压力达到模拟深水的目的。试验在中国船舶科学研究中心(江苏无锡)完成，试验用模拟深水爆炸罐及内部布置如图2所示。该模拟深水爆炸罐为球壳形结构，内腔直径7 m，最大模拟水深600 m，最大爆炸当量1.0 kg TNT。在罐体内部，采用绳索吊放装药和悬吊传感器支架，压力传感器安装在传感器支架上。

试验的TNT装药形状为近似等高圆柱，装药密度为1.60 g/cm3，试验时吊放于爆炸罐中心。试验用压力传感器为PCB-138A50型电气石水下爆炸压力传感器，垂直悬吊于距爆炸中心水平距离490 mm处。试验获得了10 g药量模拟400 m、500 m和 600 m 水深以及30 g、50 g药量模拟600 m水深共5个工况的有效数据，实测的典型(装药质量10 g，模拟水深400 m)压力p-时间t曲线如图3所示[19]。所获得的模拟深水爆炸二次压力波超压峰值的试验结果和应用所建立数值模型针对试验工况的仿真结果，一同示于表3。

由表3可以看出，试验值与仿真值之间存在一定偏差，偏差的产生可能有如下3方面原因：1)数值仿真与试验装药虽然种类相同，但装药密度、爆速等参数无法保证完全一致；2)试验本身存在一定的随机误差；3)数值仿真存在着不可避免的算法误差。尽管如此，数值仿真与试验结果的偏差均保持在±10%以内，二者吻合度和一致性良好，可以认为数值模型正确合理、能够满足工程研究需要，可用于深水爆炸二次压力波问题的研究。

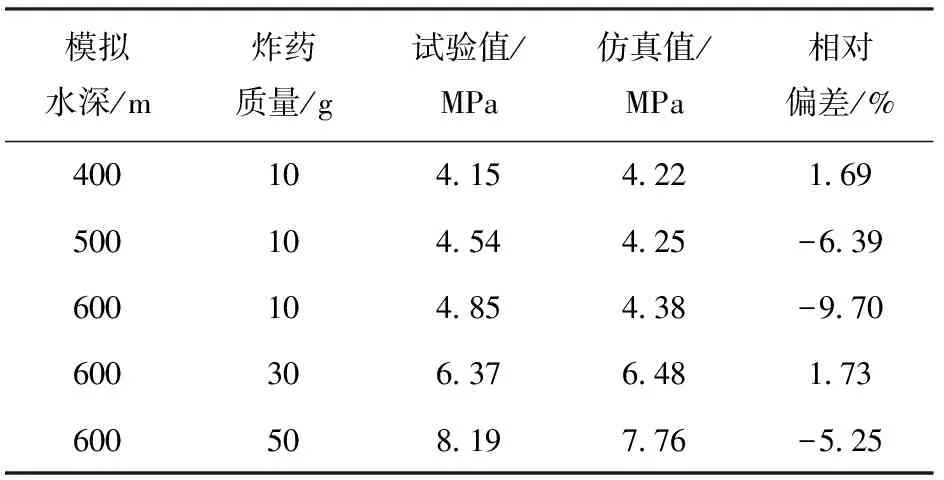
表3 二次压力波超压峰值的试验与仿真结果

3 数值计算与数据分析

3.1 数值计算与结果

采用经过试验数据校验的上述数值模型，进行30 g TNT球形装药5～8 000 m水深范围内共 18个工况的计算，装药半径R0为16.48 mm，分别在R/R0(R为爆距)取值为10、15、25、35和50倍装药半径处设置流场观测点并采集当地的压力历史。所提取的典型流场观测点(水深H=2 000 m、R/R0=25)压力-时间曲线如图4所示。图4中，Δp2表示二次压力波峰值压力与静水压力之差，称为压力波超压峰值。由图4可以清楚地看到，爆炸冲击波及随后的脉动压力波。

通过数值计算获得不同水深和爆距条件下Δp2的仿真数据，如表4所示。需要指出的是，表4中并没有给出0 m水深的数据。事实上，按0 m水深的参数设置，实际计算中会出现明显的数值振荡现象，难以得到满意的计算结果，这可能是由软件和数值算法自身的原因所导致的。另外，理论上的0 m水深爆炸实际并不存在，其Δp2只是一个虚拟外推值。对于这个虚拟外推的0 m水深Δp2，可以利用表4数据通过拟合得到，且比刻意的直接计算更具有科学合理性。

表4 Δp2的仿真结果

根据表4的数据，得到二次压力波超压峰值Δp2分别随水深H和R/R0的变化趋势，如图5和图6所示。

由图5可以看出，对于全部的5个爆距观测点，二次压力波超压峰值Δp2均随水深H的增加而不断升高，但上升趋势渐缓。即随着水深增加，二次压力波超压峰值不断增大，增大比率不断减小。

由图6可以看出，固定水深H条件下，二次压力波超压峰值Δp2随R/R0的增大而不断降低，与爆炸相似律所描述的变化趋势相类似。事实上，由于数值计算的装药质量W固定为30 g，可通过数据变换分析Δp2与相似参量W1/3/R的关系。

3.2 数据分析与Δp2工程模型

以爆炸相似律为理论基础进行模型构造，在此基础上对仿真结果进行深入的数据分析，研究水深对二次压力波传播的影响以及Δp2的工程计算方法。

3.2.1 模型构造

经典文献[3-4]给出了不考虑水深影响的TNT装药Δp2爆炸相似律计算公式：

(4)

对于深水爆炸Δp2的模型构造，首先需要进行两点假定：

1)固定水深条件下的深水爆炸，Δp2只与参量W1/3/R有关，即符合爆炸相似律；

2)水深H和相似参量W1/3/R对Δp2的影响各自独立。

基于爆炸相似律并参考经典模型(4)式，构造深水爆炸Δp2工程模型的一般形式为

(5)

式中：k、α为常数；f(H)为与水深H相关的函数，体现为一种水深修正，f(H)需要满足H=0 m时f(H)=1。对比(4)式和(5)式可以看出，前者是后者的一个特例。

3.2.2 数据分析

(5)式包含两个变量：相似参量W1/3/R和水深H，如果能确定常数α和k以及函数f(H)，就可以得到深水爆炸Δp2工程模型的显式表达式。下面对数值仿真结果进行数据分析，同时阐述相关假定以及模型构造的合理性。

对(5)式等号两边同取对数，得

ln Δp2=lnk+αln(W1/3/R)+ln[f(H)]

(6)

考虑(6)式的函数和变量形式，对表4的数据进行换算，得到表5，其中ln(W1/3/R)由R/R0按W=30 g换算得到。根据表5的数据，可以绘制出不同水深H下的ln(Δp2)～ln(W1/3/R)关系曲线和不同ln(W1/3/R)下的ln(Δp2)～H关系曲线，分别如图7和图8所示。

表5 不同H和ln(W1/3/R)下的ln Δp2

由图7可以看出，给出的5种水深(其他深度亦如此)的ln Δp2～ln(W1/3/R)曲线均为直线且相互平行，表明水深一定时二次压力波超压峰值Δp2只与相似参量W1/3/R有关，即Δp2符合爆炸相似律且为以常数α为指数的关于W1/3/R的幂函数。由图8可以看出，5种相似参量W1/3/R的ln Δp2～H曲线形状是一致的，相互之间可通过平移实现不同W1/3/R间的转换，表明水深H对任意W1/3/R取值的Δp2的影响都是相同。图7和图8的曲线的“直线-平行”和“相同-平移”特征，表明相似参量W1/3/R和水深H或函数f(H)对Δp2的影响各自独立。由此可见，模型构造的两点假定符合客观实际，Δp2工程模型的一般形式是科学合理的。

由图7结合(6)式可知，ln Δp2～ln(W1/3/R)直线的斜率为α，截距为lnk+ln[f(H)]。考虑(6)式并在表6基础上进行进一步数据处理，得到不同H下的α和lnk+ln[f(H)]示于表6。

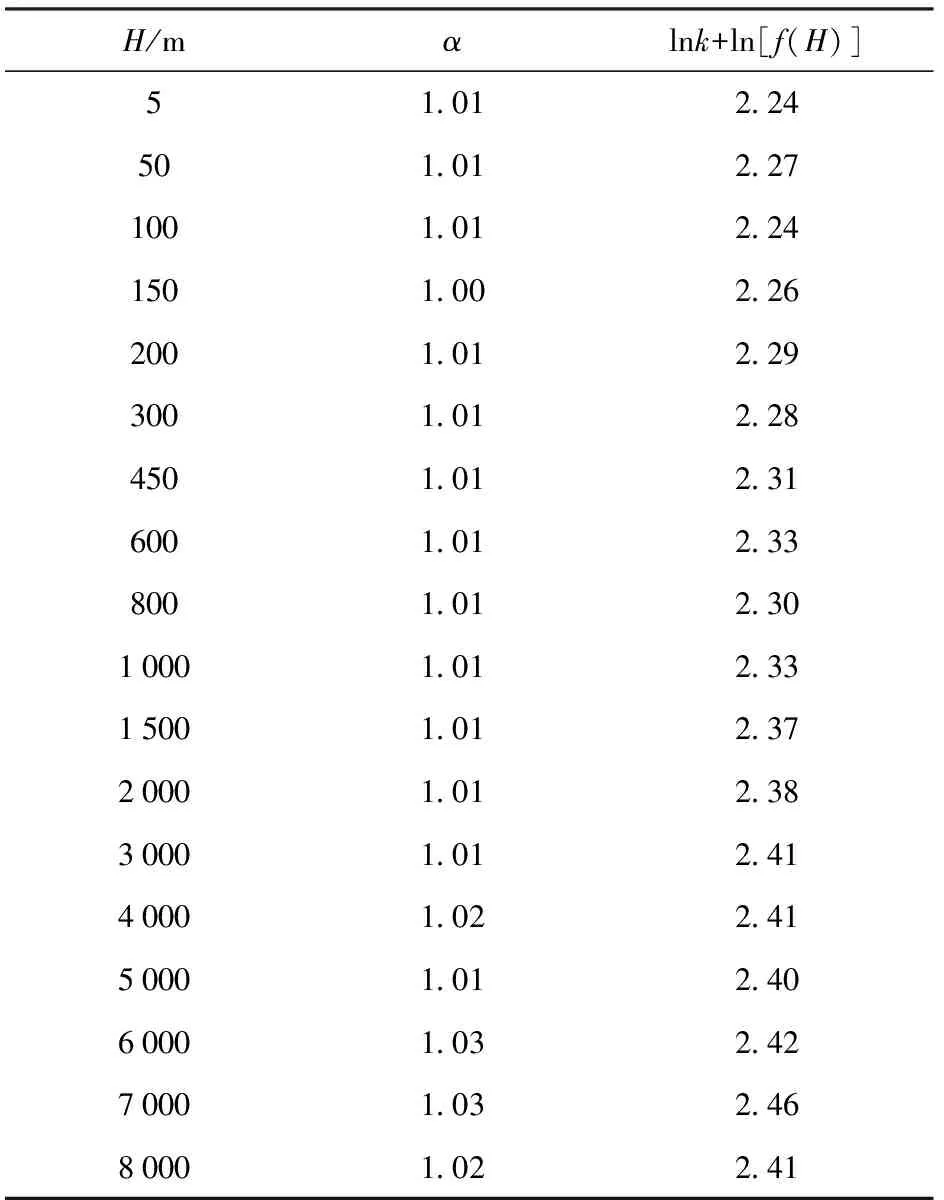
表6 不同H下的α和lnk+ln[f(H)]

1)(5)式中常数α的确定

综合分析图7和表6，可以认为所计算的每一水深的ln Δp2～ln(W1/3/R)曲线均为直线且斜率均近似为1。考虑到仿真误差的存在，取α=1是合理恰当的，与经典文献[3-4]以及USNOL[17]的试验结果完全一致，也使本文研究与经典成果实现了相互印证。

2)(5)式中常数k的确定

对于一般形式的(5)式，在已确定α=1的条件下，再考虑f(H)的定义所给出的H=0 m时f(H)=1，理论上很容易由H=0 m的Δp2值直接确定常数k。然而如前所述，由于难以得到H=0 m的Δp2精确计算值，需要通过数据拟合外推得到k值。

根据表6的数据，绘制以水深H为自变量的lnk+ln[f(H)]散点图，进而得到lnk+ln[f(H)]关于水深H的拟合曲线，如图9所示。对于拟合曲线与lnk+ln[f(H)]轴的交点，存在H=0 m，f(H)=1，ln[f(H)]=0，于是lnk+ln[f(H)]=lnk，最终得到lnk=2.234 5，k=9.34。

3)(5)式中f(H)的确定

常数k确定之后，由表6数据可进一步得到18组[H,f(H)]数据。通过绘制[H,f(H)]数据散点图然后进行数据拟合，并使拟合函数满足H=0 m时f(H)=1，最终得到f(H)与H的关系如图10所示。

拟合函数f(H)为

f(H)=1+0.006 1·H0.41

(7)

拟合函数f(H)的R2值约为0.92，表明拟合精度是可以接受的，能够满足一般的工程计算需要。

3.2.3 TNT炸药的Δp2工程模型

由TNT球形装药的数值仿真结果，通过数据分析确定了(5)式中的常数α、k以及水深修正函数f(H)。从而获得了适用于TNT炸药深水爆炸、基于爆炸相似律结合水深修正的计算二次压力波超压峰值的工程模型，即

(8)

式中：Δp2的单位是MPa，W的单位是kg，R、H的单位均为m，其适用范围为本文模拟深度0～8 000 m。

为进一步充分验证工程计算模型(8)式的有效性和正确性，将试验值和相同条件下的计算值进行对比，如表7所示。从表7中可以看出，(8)式与试验值的相对偏差平均在10%以内，表明该工程计算模型具有较好的计算准确性和工程实用性。

表7 试验值与(8)式的Δp2计算值对比

4 分析讨论

4.1 深水爆炸二次压力波超压峰值的相似律

由图7和表6可以清晰地看出，任意水深条件下的ln Δp2～ln(W1/3/R)曲线均为直线且相互平行，对应不同水深的直线间可以通过相互平移得到，其间的平移变换受水深修正函数f(H)控制。表明任意水深条件下的Δp2均符合爆炸相似律，其数学形式为以常数α为指数、关于变量W1/3/R的幂函数。本文的数值仿真及数据分析表明，对于球形TNT装药α取值为1，与经典文献[3,4,17]完全一致。需要指出的是，经典文献[3-4]的(4)式中k取值7.095，与本文9.34不同。其中的主要原因可能是装药条件不同，AUTODYN材料库的TNT装药密度为接近理论密度的1.63 g/cm3，爆轰和JWL状态方程参数均与此相对应，而经典文献[2]的结果主要是来自于密度为1.50～1.55 g/cm3铸装药的研究。

4.2 水深对二次压力波超压峰值的影响

深水爆炸二次压力波超压峰值Δp2符合爆炸相似律，意味着相似参量W1/3/R相同时，水深对Δp2的影响由函数f(H)所体现。由图10可以看出，f(H)随水深H的增大连续单调递增，水深越浅、增长越快。由图10可以直观看出，水深由0 m到1 000 m，f(H)值从1.0增大到约1.1，增长了10%；而f(H)约从1.1增大到1.19，增长不到9%，需要水深由1 000 m增加到5 000 m。另外，由f(H)导数f′(H)=0.002 5H-0.51的函数图像，也能够清晰地看出二次压力波超压峰值随水深的变化规律。

二次压力波超压峰值随水深的变化，也是水下爆炸中气泡能随水深增加而不断增大、冲击波能和气泡能分配比例随水深而变化在一方面的体现。但二次压力波超压峰值随水深“先快后慢”的变化趋势，其背后的力学机制还有待进一步探讨。

4.3 深水爆炸Δp2的工程模型

如前所述，水深H和相似参量W1/3/R对深水爆炸二次压力波传播的影响是相互独立的；固定水深H条件下，二次压力波超压峰值Δp2符合爆炸相似律；固定相似参量W1/3/R条件下，二次压力波超压峰值Δp2随水深增加具有相同的水深修正函数f(H)。因此，基于爆炸相似律结合水深修正构造Δp2工程模型的基本思路以及如(5)式的基本形式是科学合理的。

对于如(5)式的工程模型一般形式，炸药类型不同，其爆炸相似律常数α、k取值不同。水深修正函数f(H)与炸药类型无关，从定义角度需要满足H=0 m时f(H)=1，理论上应该是统一的。因此，如(5)式的二次压力波超压峰值Δp2工程模型的一般形式，具有通用性和扩展性。需要指出的是，本文通过数据拟合得到的如(7)式的f(H)函数形式，其准确性和普适性尚需进一步的研究确认。

对于TNT球形装药，通过有试验依据的数值仿真及进一步的数据分析，确定了爆炸相似律常数α、k的取值以及水深修正函数f(H)的表达式，从而获得一种适用于TNT炸药深水爆炸、基于爆炸相似律结合水深修正的计算二次压力波超压峰值的工程模型—(8)式。由于数值模型及其计算结果经过了实验校验，可以认为该模型具有工程实用价值。