考虑混合车型模式的地铁接驳公交优化研究
2022-11-30李佳杰刘向龙李香静刘好德
李佳杰,刘向龙,李香静,刘好德
(1.交通运输部科学研究院,北京 100029;2.城市公共交通智能化技术交通运输行业重点实验室,北京 100029)
0 引言
《交通强国建设纲要》[1]提出“推动交通发展由追求速度规模向更加注重质量效益转变,由各种交通方式相对独立发展向更加注重一体化融合发展转变”的要求。在此背景下,出行即服务(Mobility as a Service,MaaS)通过整合多方式的出行服务,进而满足乘客一站式、门到门的出行需求,为下一阶段各种交通方式的一体化融合发展提供了路径[2]。轨道交通与公交作为城市公共交通的主体,目前面临换乘衔接不畅、地铁站周边出行“最后一公里”问题突出等问题,两者的融合发展尤为迫切。接驳公交作为常规公交的一种补充,主要在早晚高峰期串联居民小区与地铁车站,对于促进轨道公交两网融合发展、解决地铁站周边区域“最后一公里”问题都有着重要意义。为此,有必要深入研究地铁车站的接驳公交设计问题,以提高城市公共交通的服务水平,推动MaaS理念落地实践。
国内外学者针对接驳公交线网设计问题(Feeder Bus Network Design Problem,FBNDP)展开了深入研究。如Kepaptsoglou等[3]提出了接驳公交服务的设计框架,包括设计候选路径及公交分配;Kuah等[4]以铁路系统接驳公交网络设计为例,设计了简化的矩形路网结构,并建立了考虑“多对一”和“多对多”两种需求模式的数学模型。之后,为更符合现实情况,不少学者提出了基于现实路网结构的接驳公交线网优化模型,以降低乘客出行成本和企业运营成本[5-8]。由于公交路径及发车频率整体优化时解空间较大,难以求得高质量解,不少学者尝试两阶段优化方法:第一阶段采用K 短路等算法求解候选公交路径集;第二阶段采用遗传算法等启发式方法选择最优公交线网[9-10],如Suman等[11]为保证计算效率,约束候选公交路径的长度不能超过最短路径的一定倍数;Zheng等[12]在此基础上,通过划分接驳公交的开行区域来降低问题复杂度。随着研究的深入,学者们进一步拓展了既有模型,使之更加贴合现实情形,包括考虑可变客流需求[13]、多种交通方式下乘客选择行为[14]、“多对多”客流需求[15]、乘客换乘行为[16]、数据驱动的出行特征精确获取[17]等。此外,“多对一”客流需求下的接驳公交线网优化问题与传统车辆路径问题(Vehicle Rout⁃ing Problem,VRP)具有相似性,奇格奇等[18]建立了接驳公交多轮次路径优化模型,探寻各车辆在各轮次的最佳运行线路。
整体上,既有研究丰富了FBNDP场景,为开展接驳公交服务提供了理论指导。然而,为减小问题的复杂度,既有研究仅考虑了单一车型模式,且公交站点仅允许单线接驳,研究场景与现实情况仍存在一定偏差,有待进一步完善:①多样化公交车型有利于适应不同客流需求特点、降低运营成本,且接驳公交多穿梭于城市支路,可开行公交的车型受道路属性限制,有必要充分考虑混合车型模式;②既有研究多假设各公交站点仅一条接驳线路,由于每个站点客流需求存在差异性,线路发车频率取决于最大客流需求车站,导致其余车站运能浪费;③在求解算法方面,由于算法与模型特点结合度不够紧密,求解效率仍有待提升。为更好地完善接驳公交服务,提升地铁站周边“最后一公里”运输效率,本文将在既有研究的基础上,充分改进上述3 点不足,建立更符合实际的地铁接驳公交线网两阶段规划模型:第一阶段采用动态规划和分支定界法思路生成高质量的候选公交路径集;第二阶段考虑站点被多条线路接驳、道路属性、车辆满载率等因素,优化公交路线、车型和发车频率,并设计定制化遗传算法,通过编码形式、约束处理、染色体等方面针对性调整,减少无效解的产生。最后,以长沙月亮岛西地铁站周边区域为案例,验证本文模型及算法的有效性。
1 问题描述
本文研究城市轨道交通车站周边区域的接驳公交线网规划问题,以解决地铁出行“最后一公里”问题,提高乘客出行效率。如图1 所示,已知地铁站和各公交候选站点(主要为小区出入口、重点公共场所等)位置、城市道路网信息及各公交候选站点的客流需求,设计最优接驳公交线网(由多条公交线路组成),并确定各线路的配属公交车辆类型及发车频率。

图1 接驳公交网络道路及车站位置示意图
由于公交线路的走向和数量、各线路配属公交车辆类型及发车频率均直接关乎乘客利益(如乘客等待时间、在车时间等)和运营单位成本等,故以乘客和运营单位整体利益最优为目标进行接驳公交优化。由于接驳公交线网包括多条公交线路,而每条公交线路又由若干公交停靠站点顺序组成,解空间较大且问题复杂。因此,采用两阶段优化思路:首先,从地铁接驳公交站出发,根据公交线路最小/最大停站数量、最短/最长运行距离、最大非直线系数等约束条件筛选若干候选公交线路;然后,基于候选公交线路集合进行接驳公交优化,从而大幅提高求解效率。
接驳公交优化时,将在既有研究基础上,充分考虑混合车型模式、车辆满载率和道路属性对车型的约束,且允许站点与多条公交线路衔接,力求更加符合现实环境。其中,城市道路属性对可开行公交车型的限制约束指不同的道路属性具有不同的允许开行车型,如图1中道路属性1,2,3分别对应高、中、低3 种等级:低等级道路仅可开行小型车;中等级道路可开行中型和小型两种车型;高等级道路可开行所有车型。根据公交线路途经的瓶颈道路(即最低等级道路),可确定该线路的允许开行车型。“允许站点被多条公交线路衔接”指本文模型将改进既有方法仅允许单线接驳的规则,各公交站点允许多线接驳,以充分契合不同站点客流需求差异较大的特征,提高运能供给与需求的匹配度。需要注意的是,在多线接驳下,车辆满载率需根据同时经过前序站点和本站的累计客流需求与线路运能的比值来确定,由于部分线路可能途经前序站点而未途经本站,故需确定各站点对应各线路的客流需求。
本文的模型基于以下假设[5-8]:
(1)本文研究衔接地铁站的接驳公交线网设计,只考虑普通公交站与地铁公交站之间的客流需求,忽略普通公交站间的客流需求;
(2)每个公交候选站点位置和原始客流需求已知;
(3)由于出行距离较短,不考虑乘客在途中的换乘;
(4)接驳公交线路实行站站停方案,不考虑甩站运行;
(5)为了便于运营管理,一条接驳公交线路仅可分配一种公交车型。
2 接驳公交候选线路集
为保证运营服务水平和公交公司利益,接驳公交候选线路的开行距离和停站数量应满足上下限要求。同时,为避免产生较大绕行的线路,本文特别考虑线路非直线系数约束,即线路新加入站点需满足线路总长度与该站点至起点的最短距离的比值小于最大非直线系数值,且线路禁止多次经过同一公交站点,从而生成高质量的候选线路集。
基于上述约束,并考虑公交候选站点间的道路连接情况,可从地铁接驳公交站出发,采用动态规划和分支定界法的思路依次产生所有满足约束的候选线路集,具体如下:
步骤1:根据公交候选站点和道路连接情况构建无向图网络G=(V,A,W)。其中,V为公交站点集合;A为V中各公交站点对构成的边集合,A={aij|aij=(vi,vj)},aij为从站点vi至vj的边;W为边的权重系数集合,W={wij|wij=w(aij)},wij为边aij的长度(km)。
步骤2:采用Dijkstra 算法[19]计算各公交候选站点vi至起点(地铁接驳公交站)的最短距离di(km),记dmin(vi,v1)=di,∀vi∈(Vv1),其中v1为起点车站。
步骤3:参数初始化,阶段k=1,起点(地铁接驳公交站)的状态s1(v1)=0,最小、最大开行距离分别为lmin和lmax,最小、最大停站数量分别为kmin和kmax,最大非直线系数值为λ,候选集合P=∅。
步骤4:利用状态转移方程,依次计算上一阶段k中所有站点vi的所有相邻点vj的状态值sk+1(vi,vj)=sk(vi) +wij。
步骤5:判断阶段k+1 中任一点vj是否满足非直线系数(sk+1(vi,vj) ≤λd)i、最大开行距离(sk+1(vi,vj) ≤lmax)和不重复经过同一公交站点的约束,若均满足,则不进行处理,否则需对vj进行剪枝。
步骤6:判断阶段k+1 中是否所有点均被剪枝,若是,则结束搜索,输出候选集合P,否则不予处理。
步骤7:判断步骤5 中未被剪支的任一点vj是否满足最小停站数量(k+1 ≥kmin)和最小开行距离(sk+1(vi,vj) ≥lmin)约束,若均满足,则将v1至vj的线路记录至候选集合P,否则不记录。
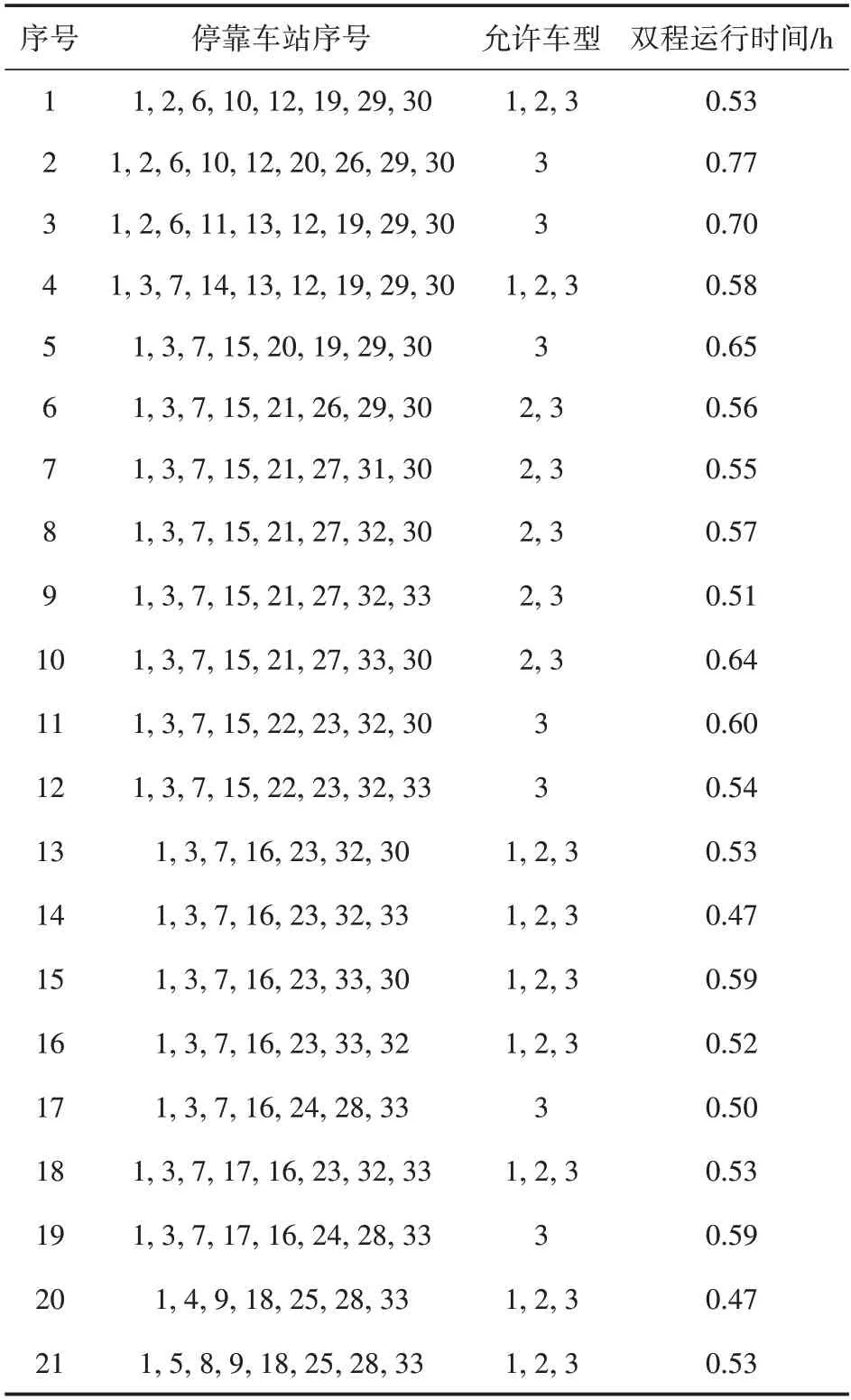
步骤8:判断是否满足最大停站数量约束(k+1 通过上述步骤,可对地铁站周边区域的候选公交站点网络进行精确搜索,高效求解所有满足约束的候选线路方案。例如,图1 网络的前4 个阶段的搜索过程如图2所示。需要注意的是,图2中阶段2的v4和v5点均出现相邻点v8,这是由图1网络G所决定的,表示两条不同的线路,需分别计算。同时,阶段3 和阶段4 存在4 个被剪枝的点,这是因为这些点均使得线路产生一定绕行,根据λ值进行了剪枝。随着阶段的增大,各点将由于最大非直线系数、开行距离等约束被剪枝,或超过最大停站数量而停止搜索,最终得到所有候选方案集合。 图2 接驳公交候选线路集产生示意图 本节根据产生的公交候选线路集,以乘客和运营单位利益最优为目标,构建以公交线路和车辆类型选择、各线路公交开行频率为决策变量的优化模型。模型在既有研究基础上,充分考虑混合车型模式、车辆满载率和道路属性对车型的约束,且允许站点被多条公交线路衔接,以全面、准确地刻画现实环境。 本文中,乘客利益包括未被满足的客流惩罚值最小和乘客出行成本(等车时间成本+在车时间成本)最小;运营单位利益包括车辆运行能耗、人员成本、车辆维修和折旧成本最小。 未被满足的客流主要来自两部分:未被最终选中车站的客流和被选中车站由于乘客等待时间过长而损失的一部分客流,具体如式(1)~式(3)所示:式(1)计算客流损失成本;式(2)计算候选车站i的乘客平均等车时间(h),当该车站未被最终选择或公交开行频率为0 时,没有乘客被服务,等车时间为0,否则为发车间隔时间的一半;式(3)表达了乘客等车时间与客流需求比例系数的关系,本文以线性4 段式划分方法为例[20],亦可根据实际需要进行调整。 式(1)~式(3)中:C1为未被满足的客流惩罚值(元);δ1为未被满足客流的惩罚系数(元/人);qi为候选车站i的原始客流需求(人);σi为候选车站i实际客流需求与原始客流需求之比;为候选车站的乘客平均等待时间(h);xp为0,1决策变量,当选择候选线路集中的线路p时,取xp=1,否则xp=0;为0,1 参数,当线路p经过车站i时,取=1,否则=0;fp为公交的开行频率(辆/h);τ1,τ2表示等待时间的划分临界值(h);a1,b1,a2,b2为线性函数的参数,均可参考既有Logit模型和实际调研数据通过曲线拟合来确定[14]。 乘客出行成本中的在车时间按式(4)和式(5)计算。由于一个候选车站可能衔接多条公交线路,因此在车时间为乘客乘坐途经该车站各线路的概率与通过对应线路到达地铁站时间的乘积。其中,乘客乘坐途经该车站各线路的概率为各线路开行频率与总开行频率的比值,如式(4)所示。 式(4)~式(5)中:为乘客乘坐途经车站i线路p的概率;为候选车站i上车乘客的全程在车时间(h);为线路p从车站i运行至地铁站的时间(h),可根据途经道路的平均运行速度(随道路属性而变化)提前确定;其余参数含义同上。 因此,出行成本可由式(6)计算,根据等车/在车时间价值系数与实际乘客人数以及乘客总等车/在车时间的乘积确定[5-8]。其中,实际乘客人数为原始客流需求与比值σi的乘积,表示乘客等待时间对客流需求的影响。 式(6)中:C2为乘客出行成本(元);δ2,δ3分别为乘客的等车、在车时间价值系数(元(/人·h));其余参数含义同上。 对于运营单位的运营成本而言,车辆运行能耗为各车型开行频率、双程运行距离及单位距离开行能耗成本的乘积,如式(7)所示[5-8]: 式(7)中:C3为运营能耗成本(元);为公交车型n的单位距离开行能耗成本(元(/辆·km));为0,1 决策变量,当线路p选择车型n时,取=1,否则=0;lp为线路p的双程运行距离(km);其余参数含义同上。 人员成本为各线路开行频率、双程运行时间及单位时间开行人员成本的乘积,如式(8)所示[5-8]: 式(8)中:C4为人员成本(元);tp为线路p的双程运行时间(h),可根据线路途经道路的平均运行速度提前确定;δ5为单位时间开行人员成本(元(/人·h));其余参数含义同上。 最后,各车型车辆的维修和折旧成本采用里程折算法计算,如式(9)所示[5-8]: 式(9)中:C5为车辆维修和折旧成本(元);为公交车型n的单位距离维修和折旧成本(元/(辆·km));其余参数含义同上。 综上,各部分成本均已转化为货币单位,可直接相加,或根据决策者需要采用不同权重系数对各部分成本进行区别。本文采用加权方法,最终得到模型总目标函数,如式(10)所示: 约束1:接驳公交线路总量约束。公交线路数量对模型目标函数具有重要影响,可对接驳公交线路的总量进行约束,即最终选择m条接驳公交线路,如式(11)所示。后续案例可对m进行灵敏度分析。 约束2:公交线路开行频率约束。各公交线路的开行频率需满足上下限约束,保证一定的服务水平,如式(12)所示。若线路p不被最终选择,则开行频率为0,式(12)恒成立。 式(12)中:fmin与fmax分别为允许的最小和最大开行频率(辆/h);其余参数含义同上。 约束3:车辆满载率上限约束。各线路的车辆满载率上限需加以约束,避免乘客留乘。车辆满载率为客流需求与提供的运输能力的比值,如式(13)所示。由于本文只考虑前往地铁站的乘客,因此各线路断面客流需求为各站客流需求之和。需要注意的是,一个公交站点可能衔接多条公交线路,断面客流需要累加多条线路的前序站点客流需求和本站客流需求,运输能力也需要累加经过本站的多条公交线路的运输能力。其中,前序站点的部分公交线路不一定途经本站,因此前序站点的客流需求仅需累加途经本站的线路需求量。 约束4:可开行公交车型约束。本文考虑不同城市道路属性对可开行公交车型的限制,如支路仅允许小车通行。由于候选公交线路提前确定,可根据线路所包含的最低等级道路提前确定各线路允许开行的公交类型,线路所分配的车型需满足道路属性要求,如式(14)所示: 本文模型为混合整数非线性规划模型(MIN⁃LP),式(2)、式(4)和式(13)涉及实数决策变量相乘,无法通过线性化手段转化为混合整数线性规划模型(MILP)。因此,采用启发式算法进行高效求解。遗传算法(Genetic Algorithm,GA)作为一种模仿生物进化过程的人工智能搜索算法,具有广泛的适用性、全局搜索能力较强、计算效率高等优点,在公交线网规划领域得到了广泛应用[6-7,13-15]。因此,本文采用遗传算法进行求解,流程如图3所示。 图3 遗传算法流程图 根据图3,首先进行参数初始化和遗传算法种群编码。然后,计算种群(本文设置数量为100)中每个个体的目标函数值,再判断个体是否满足所有约束条件,如不满足则对所对应的目标函数值进行惩罚,以便后续筛选。接着,进行遗传运算,包括选择、交叉和变异,对初始种群进行处理,产生下一代种群,并对个体染色体进行调整。最后,进行迭代计算,直至满足最大迭代次数(本文设置为200代),输出最优解。求解过程中,为保证最优性,采用精英保留策略,每代最优个体将被直接选入下一代种群。关键步骤如下: (1)编码。本文模型需决策候选公交线路序号、公交车类型和发车频率,均为整数变量,因此采用3 段式整数编码方式,如图4 所示。最终选择的公交线路数量为m,因此染色体第1、第3部分基因长度均设为m,且第1 部分基因采用Matlab 的randsample 函数产生候选公交路径序号范围内的m个不同的整数,第3 部分基因则在给定的频率范围内产生随机整数。染色体第2 部分基因长度等于候选公交路径总数,每一个基因均在对应的候选公交路径所允许的车辆类型上产生,以避免产生大量不可行方案。 图4 染色体结构 (2)约束处理。通过本文特定编码方式,可直接满足约束1、约束2 和约束4。对于约束3 需进一步判断,若不满足,则需对个体的目标函数值乘M(很大的正数,本文取10 000)进行惩罚。 (3)遗传运算。为进行遗传迭代,需对原始种群进行变化,包括选择、交叉和变异,产生新种群从而搜索更优解。选择操作采用常规的轮盘赌方法[21];交叉操作采用均匀交叉,若[0,1]内产生的随机数小于等于交叉概率(本文为0.8),则再次产生[1,m-1]内的随机整数以确定交叉位置,对两条染色体进行基因交换;变异操作则对每个基因位产生[0,1]内的随机数,若小于等于变异概率(本文中为0.2),则进行均匀变异,在步骤(1)编码阐述的范围内产生随机整数。 (4)染色体调整。经过遗传运算后,可能导致个体不满足约束1,即可能存在相同序号的候选路径。因此,本文对遗传运算后的个体进行判断,若存在相同序号的候选路径,则对重复序号所在基因位产生随机整数,直至m条候选路径序号均不相同。 (5)精英保留。为保持搜索过程中的全局最优解,并便于收敛,本文采用精英保留策略,即保留每代种群中最优个体直接进入下一代种群。 以长沙月亮岛西地铁站周边区域为研究对象,对本文方法的合理性和有效性进行验证。接驳公交网络的道路及车站位置如图1 所示。早高峰时期大量居民从居住小区前往地铁站通勤,高峰小时各候选站点的原始客流需求如表1 所示,模型相关参数取值如表2 所示,所有参数取值均来自文献[5]~文献[8]。所有案例均在配置为Intel Core i7-8550U CPU @ 1.8GHz、内存为8GB的电脑采用Matlab 2016a进行求解。 表2 模型参数取值[5-8] 根据本文第2 节接驳公交候选线路集产生方法和表2 相关参数,共计产生207 条候选公交路径。其中,主要由最小/最大停站数量之间的可行路径组成,通过人工筛选合并,确定21条候选路径,如表3 所示。可以看出,所有路径均从地铁车站出发,到达距离较远的车站30,32 和33,候选路径已包含所有车站序号,且满足停站数量和运行距离约束。 表3 候选路径集 根据表3 所示候选路径,利用遗传算法进行优化,收敛过程如图5 所示。由该图可以看出,通过本文特殊编码及约束处理方式,迭代过程中最优解始终满足所有约束,且求解效率较高,在第27 代时基本收敛到最优解,在第157 代时收敛到最优解,总耗时在10s 内,可满足实际工作的时间要求。 图5 GA收敛结果 为验证本文考虑混合车型模式、站点可被多线接驳的必要性及有效性,采用控制变量法进行对比分析:对比方法1 均采用小车型(以满足道路属性约束),车型序号为3;对比方法2 在第二阶段线路优化时不考虑途经相同站点的线路(除起点站1)。需要注意的是,由于对比方法2 的站点均只能被单线接驳,而表3 中大量线路均途经多个相同站点,无法选出m条线路(本文取m=8),因此将对比方法2 的约束1 进行松弛。对比方法1 和方法2 的其余参数均与本文方法相同,求解结果如表4 所示,各方法的车站满载率统计结果如图6所示。 表4 本文及对比方法求解结果 图6 各方法车站满载率统计柱状图 由表4 和图6 可以看出,本文方法通过多样化车型及允许车站被多线接驳,可提高服务车站数,即图6 中满载率不为0 的车站数量。同时,本文方法可有效均衡各站满载率水平,减少运能浪费和下游车站(靠近地铁的车站)的过度拥挤现象。因此,本文方法可较对比方法1 减少19.1%的总发车次数,并使得总目标函数值下降25.9%,充分证明了考虑多种车型的必要性。另外,与对比方法2 相比,本文方法由于允许车站被多线接驳,可大幅增加后续线路的选择范围,使得服务车站的覆盖率由45.5%提升至97%,总目标函数值下降显著。 基础案例仅分析了公交线路数量为8 时的情形,但公交线路数量对模型各项子目标函数值及总目标函数值具有重要影响,决策者需要根据实际情况灵活设置。因此,对公交线路数量进行灵敏度分析,即调整模型约束1的m值,观察目标函数值的变化,从而为决策者提供经验借鉴。 公交线路数量灵敏度计算结果如图7 所示,由于对比方法2 始终仅选择2 条线路,不随m值的变化而变化,因此仅分析本文方法和对比方法1 的结果。可以看出,两种方法的目标函数值均随着m值的增大而下降,且当m<6 时,目标函数下降显著;当m≥6 时,目标函数值下降趋势逐渐变缓。这是因为当m值较小时,目标函数值主要来源于未被满足的客流惩罚,m值的增大有利于扩大服务车站数,减少未被满足的乘客数(如图7 曲线所示),从而使得目标函数值快速下降;当m值较大时,未被满足的客流惩罚已较小,甚至为0,继续增大m仅能微调各项子目标函数值,而总目标函数值变化较小,甚至由于各线路最小发车频率的约束而增大总目标函数值(如m=14时,两种方法的总目标函数值均略有上升)。 图7 本文方法及对比方法1的公交线路数量灵敏度计算结果 综上,决策者在设计接驳公交线网时应尽可能地覆盖更多站点及客流,但也不宜设置过多的公交线路,否则将导致运营成本增加而乘客服务水平几乎无变化。 为了提高地铁站周边区域乘客的出行便利度,解决地铁出行“最后一公里”难题,本文以地铁接驳公交线网设计为研究对象,构建了地铁接驳公交两阶段规划模型。模型充分考虑了混合车型模式、允许站点被多线接驳、道路属性对车型限制等因素,并设计定制化遗传算法进行高效求解。案例表明,较单一车型模式、每个站点仅允许单线接驳等既有方法,本文方法可显著降低总发车次数、扩大服务车站数,目标函数优化率超过25%。所提方法可为地铁站点周边区域的接驳公交线网设计及运营计划编制提供参考,推动多模式交通一体化融合发展。然而,由于未充分考虑小汽车、自行车等多种交通竞争模式下的乘客选择行为,接驳公交客流需求可能存在一定误差,未来可进一步嵌套多方式竞争下乘客选择Logit 模型,以更精确地确定接驳公交的客流需求。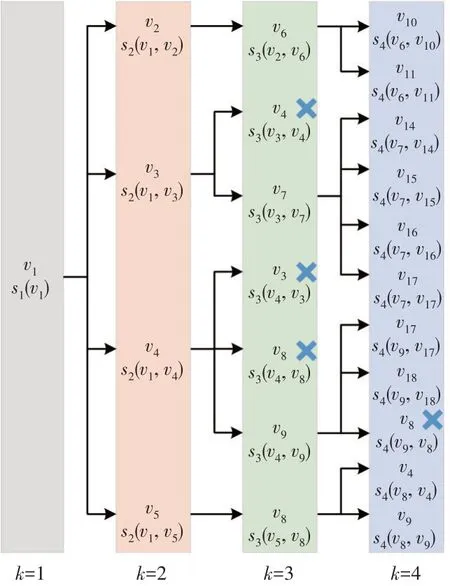
3 线路选择和公交配置优化模型
3.1 模型目标
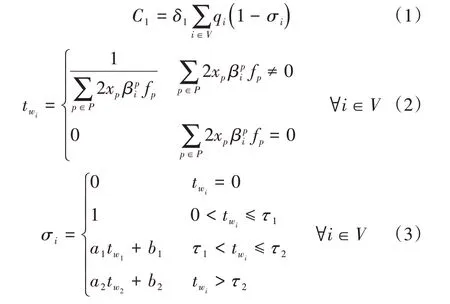

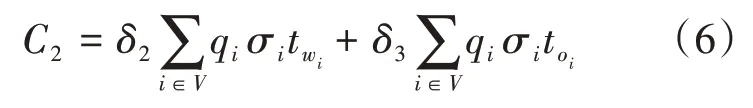




3.2 约束条件



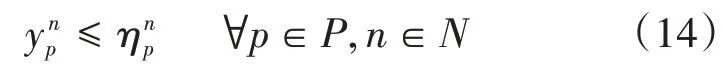
4 算法设计


5 案例分析
5.1 案例参数
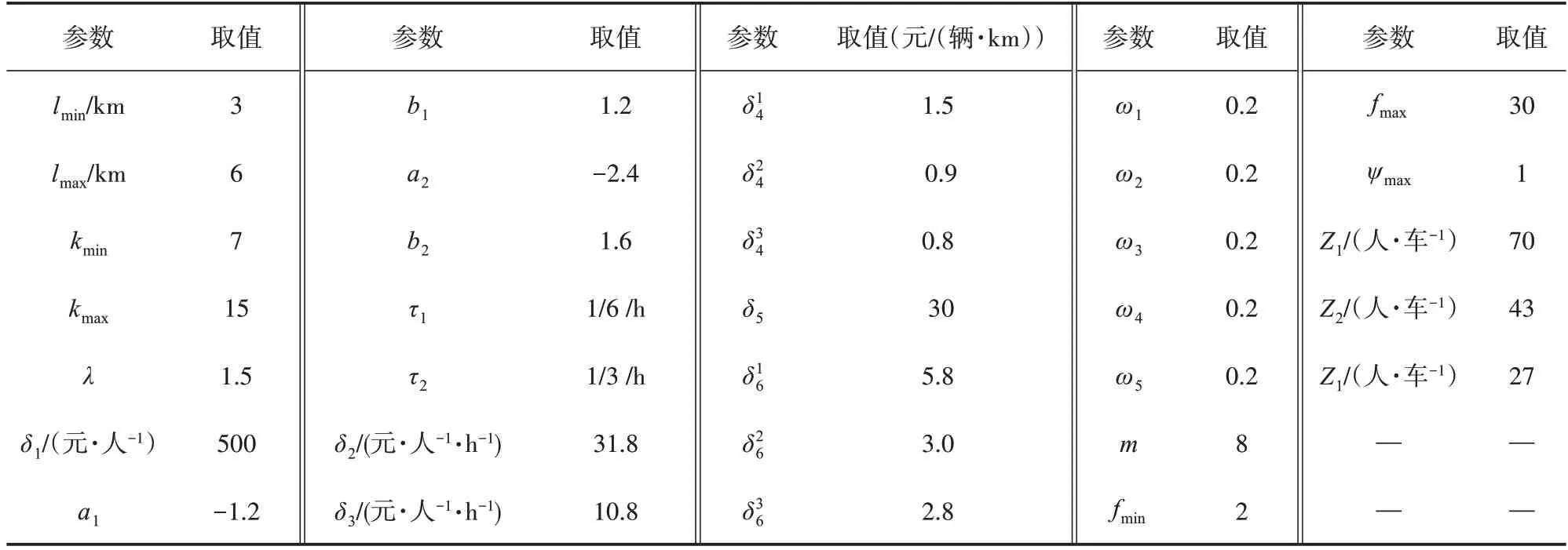
5.2 模型效果分析


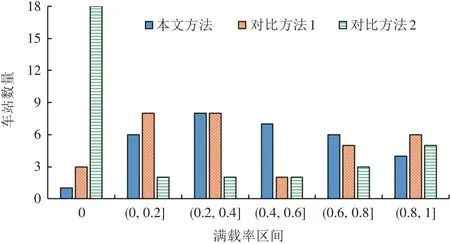
5.3 公交线路数量及灵敏度分析
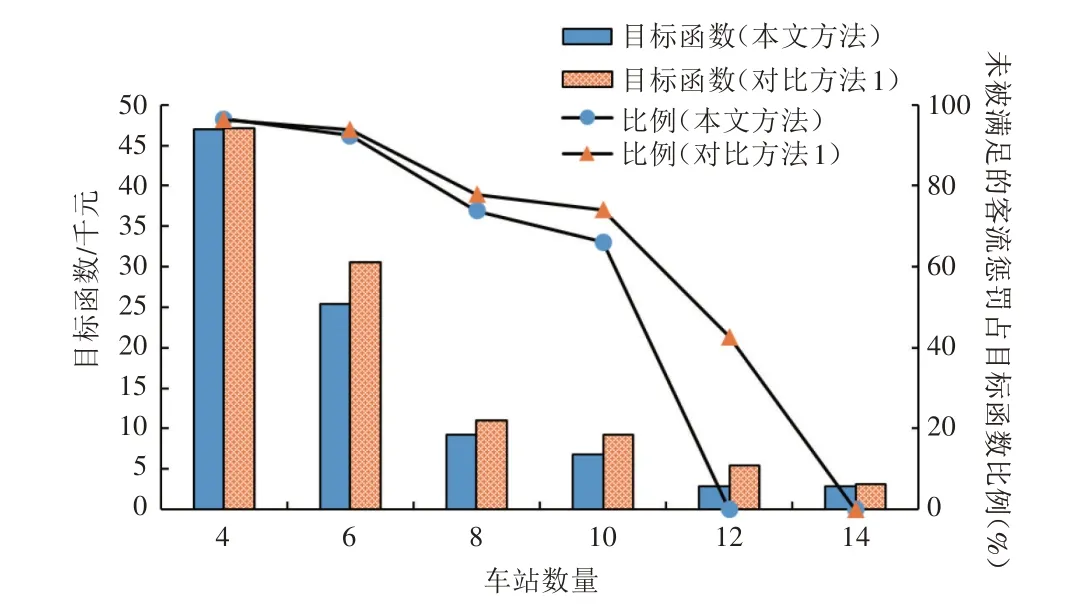
6 结语
