对外客运枢纽出租车接续运输供需匹配度评价方法
2022-11-30吴玉兰陈旭蕊柴娇龙翁剑成孙宇星
吴玉兰,陈旭蕊,柴娇龙,翁剑成,孙宇星
(1.北京市交通委员会,北京 100088;2.北京工业大学 交通工程北京市重点实验室,北京 100124)
0 引言
随着我国城市综合交通枢纽一体化规划和建设的推进,现已基本形成民航、铁路与城市轨道、公交、接驳巴士、出租车、网约车等多模式交通衔接的接续运输体系,衔接换乘关系日趋复杂。因抵达客流存在短时间内集聚性强、高峰小时突发人流量大等特点,容易造成枢纽接续运输效率低,导致整体接续运输服务质量偏低。对于出租车接续方式而言,枢纽周边路网高峰时段易发生拥堵,出租车抵离等候耗时通常较长,且由于接续客流需求规模的波动而常导致部分时段存在出租车运力不匹配等情况,尤其在夜间、不利天气、节假日高峰等特殊时段,出租车需求量显著增加,供需矛盾突出,应急运输保障能力明显不足。因此,结合抵达客流特征和出租车的运力容量,开展出租车接续运输供需匹配评价方法研究,定量化评价出租车客流的供需匹配程度,前瞻性地开展接续运输的运力调整和调度优化,有助于提升枢纽接续运输保障能力和服务水平,减少旅客滞留时间。
国内外学者在出租车运能匹配等相关方向开展了诸多研究。为了解决出租车运能供需不匹配等相关问题,一些学者先后提出多种分析方法并构建了相关优化和评价模型,如曹洁等[1]从宏观与微观角度分析了市内打车难的问题,构建了基于Volterra 模型的网约车系统供求匹配数学模型,探究了网约出租车供需匹配中各因素间的相互制约关系。一些研究从运营成本最小化、司机收益及乘客效益最大化角度出发,探究接续运输供需匹配情况,如Tran等[2]提出了一种新的解决出租车与乘客负荷平衡的方法,在最大限度地减少供需失衡的同时,尽可能地使司机的潜在利益最大化;孙浩[3]在兼顾乘客和运营商利益的原则下,构建了综合客运枢纽对外及对内交通方式的运能测算模型,提出了基于主导方式的运能匹配规划方法;贺艳琴[4]以司机和乘客的整体效益为目标,优化出租车资源分配,研究不同时空出租车资源的供求匹配程度,以缓解打车难的问题。为解决机场出租车调度管理中司机与乘客间信息不匹配的问题,钱鹏程等[5]采用二叉树决策模型等方法,构建了司机决策的均值模型和收益模型;朱桂玲[6]从运营者角度出发,通过调查机场出租车公司运营现状,构建出租车供需匹配率模型,探寻各种条件影响出租车司机行为决策的机理,最终构建了出租车司机选择决策模型。还有一些研究从减少候车时间出发,探究接续运输供需匹配情况,如蔡赫等[7]以出行者候车时间最短为目标,建立出租车运力投放最优化模型,并采用遗传算法进行求解;任其亮等[8]同样进行了运营组织方面的研究,以接续方式选择模型为约束,构建了以运营及乘客等待时间成本最小为目标的出租车运营通道优化模型;徐硕等[9]等围绕出行OD识别、出行方式识别以及人群识别3 个算法探究出租车接续运输规律,基于细时间颗粒度分析了北京西站接续旅客数与候车时间,评价了不同时段枢纽场站的出租车供需匹配情况。还有部分研究同时考虑了各种效益与等待时间等因素,从而探究出租车供需情况,如赵开妍等[10]综合考虑换乘等待时间及运营成本,基于排队论建立出租车换乘效率优化模型;Manski等[11]在探究出租车供需情况时,提出将价格和等候时间作为乘客选择出租车时的潜在考虑因素,出租车公司后期运营优化重点放在空载消耗的费用上;玛依拉·艾则孜等[12]综合考虑乘客乘车费用、平均乘车时间和平均等候时间构建供需匹配模型,并采用模糊综合评价和多元回归模型,基于西安市滴滴快智能出行平台数据,推导出西安市出租车供求平衡情况。
总体而言,现有国内外研究主要基于乘客等待时间、司机收益、运营成本等因素建立出租车供需匹配评价模型。然而,对外客运枢纽的出租车系统情况复杂,有无出租车蓄车场、蓄车场的出租车数量、乘客滞留情况等都会对运力供给和需求产生影响。为了科学评价出租车接续运输供需匹配情况,本文基于对外客运枢纽出租车接续运输的需求和供给数据,综合分析接续运输客流需求与运力供给特征,结合蓄车场条件、出租车数量、出租车运力供给能力以及出租车候车点排队人数等实际情况,进一步研判出租车运力缺口,采用SBC 方法,分场景构建出租车供给充足和供给不足的供需匹配评价模型,并引入运能匹配度指标,定量评价出租车接续运输供需匹配情况,最后通过案例应用将模型所求平均等待时间与实际测算的平均等待时间进行对比,验证模型的准确性,旨在为提升对外客运枢纽场站的出租车接续交通运输服务水平提供支撑。
1 数据来源
对外交通枢纽各接续运输方式的客流及运力数据,是开展接续运输客流特征分析与供需匹配评价的重要基础。本文对外客运枢纽场站数据来源于北京市综合交通枢纽接续运输运行监测平台,具体包括抵站客流数据、出租车接续运输数据及出租车运力数据,对应的数据类型及包含字段如表1所示。

表1 客流及运力数据表
表1 所示出租车运力数据中,平均载客率为枢纽场站内每辆出租车的平均载客人数;平均服务率为枢纽场站内每辆出租车单位时间内所能服务的平均乘客数;单个出租车服务强度为乘客到达率与平均服务率的比值,其中乘客到达率为单位时间内到达的乘客数;出租车整体服务强度为每辆出租车服务强度与单位时间内可提供服务的出租车数量的比值。
2 出租车接续运输的供需匹配度评价
2.1 出租车接续运输实际场景分析
综合客运交通枢纽站对外客运枢纽抵达旅客的出租车接续运输问题属于典型的排队论问题,可以采用排队论中的M/M/C 排队模型[13]来表示。M/M/C 是一种单路排队多通道的排队模型,其中第1 个M 指输入过程中顾客相继到达的间隔时间服从负指数分布;第2 个M 指服务时间服从负指数分布;C 表示服务台个数(即同一时间同时服务的出租车数量)。该模型的排队系统如图1 所示,其中“T”代表出租车,“P”代表乘客。
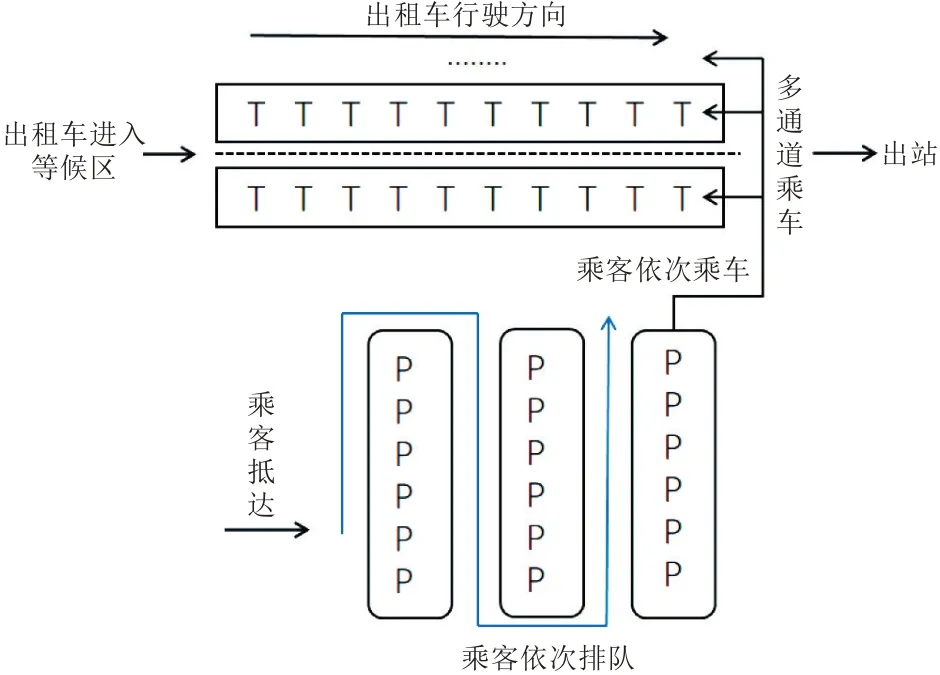
图1 基于M/M/C排队模型的对外客运枢纽出租车排队区示意图
实际上,乘客排队现象在枢纽出租车接续运输中时常出现,很多情况都会导致出租车供给不足,例如高峰时期单位时间内换乘旅客激增,而出租车数量有限,且由于行李箱、背包等各种随身物品的上下车搬运,导致出租车平均服务时间较长,车辆供给不足,出租车的平均来车频率较低,所以单位时间出租车服务强度大于1 的次数较多。此外,航班或列车的到达时间决定旅客进出站时间,交通枢纽内出租车数量随之产生变化,在大量航班或车次到达客运枢纽站,旅客换乘需求显著增加时,出租车供不应求甚至无车可供的情况时有发生。因此,对于出租车候车区排队特点的分析是十分必要的。
为了更准确地评估乘客排队时间,确定换乘出租车的运能匹配度,本文根据出租车排队特征以及出租车的供给情况,分出租车供给充足和供给不足两种情况进行探讨。出租车供给充足是指出租车蓄车场车辆充足,一般情况下可保证所有乘客无需排队等待即可顺利乘车离站;出租车供给不足是指出租车蓄车场没有足够车辆供所有乘客即刻出行,乘客需等待出租车到达。当出租车供给充足时,也存在高峰时期旅客激增,接续运输供需不平衡的情况。因此,本研究在出租车供给充足的情形下,又根据乘客到达率将出租车服务系统分为出租车整体服务强度大于1 和小于1两种情况。当出租车供给不足时,通过计算出租车的平均到达时间间隔,对出租车的服务时间和服务效率进行修正,根据M/M/C 排队模型,引入出租车供需匹配度指标,即符合乘客期待的排队时长,确定单个乘客不同情况下的平均排队时长,通过比较分析,判断各情况下出租车供需匹配情况。其中,若实际值大于出租车供需匹配度指标,则供需匹配较差;反之,则供需匹配较好。
2.2 供给充足条件下的供需匹配评价模型
出租车接续运输的排队问题属于非平稳到达排队问题,而平稳排队模型是估计非平稳到达排队系统的主要方法之一。该模型有多种估计方法,包括逐点平稳估计法、平均平稳估计法及积压后移平稳估计法(Stationary Backlog-Carryover approach,SBC)等。其中,SBC 因可以较好地处理排队相关问题,已在许多领域得到广泛应用,如解决轮胎紧急修复问题[14]、分析队列阻塞概率[15]、非平稳到达码头的集卡预约优化[16]等,故本文采用SBC 方法进行出租车接续运输供需匹配评价。在实际出租车接续运输中,即使在出租车供给充足的情况下,也可能存在高峰时段内客流量激增、接续运输有限、接续换乘服务时间较长的问题,所以需针对出租车整体服务强度大于1和小于1两种情况分别进行研究。
SBC 方法包含两个阶段:第一阶段,估计期望的出租车利用率,同时引入损失模型将当前时段不能服务的顾客转移到下一个时段服务;第二阶段,基于出租车的利用率估算队长。研究首先将每天要预测的时间段划分成N个时段t1,t2,…,ti,…,tN,t(ii=1,2,…,N)表示第i个时段,每个时段内乘客的到达率、服务率不变。
2.2.1 第一阶段
首先,计算第i-1 时段单位时间内的乘客转移率:

式(1)中:bi-1为第i-1 时段单位时间内的乘客转移率(人/min);为第i-1 时段单位时间内的修正到达率(人/min);Pi-1(B)为第i-1 时段到达乘客的损失率(%);μi-1为第i-1 时段单位时间内出租车的服务率(人/min);Gi-1为第i-1时段内出租车能够同时提供服务的车辆数(辆);k为常数,取k=0,1,…,Gi-1。
然后,计算下一时段修正的乘客到达率,即初始乘客到达率与由上一时段转移的乘客转移率之和:

式(2)中:为第i个时段修正的乘客到达率(人/min);λi为单位时间内初始乘客的到达率(人/min);bi-1含义同前。
最后,计算下一时段出租车的利用率:
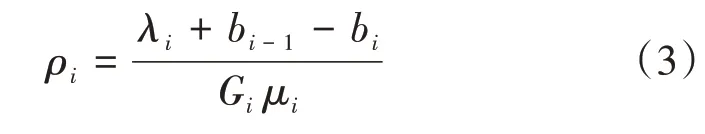
式(3)中:ρi为第i时段出租车的利用率(%);Gi为第i时段内出租车能够同时提供服务的车辆数(辆);其余变量含义同前。
2.2.2 第二阶段
首先,基于出租车的利用率和乘客转移量估算队长:
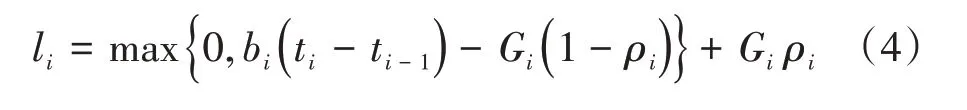
式(4)中:li为第i个时段内的排队长度(人);bi(ti-ti-1)为第i个时段内累积转移的乘客数(人);Gi( 1-ρi)为第i个时段内出租车的服务能力(人);bi(ti-ti-1)-Gi( 1-ρi)为第i个时间区间结束时的队长(人);其余变量含义同前。
接着,估算出租车整体服务强度大于1 时的队长lD:
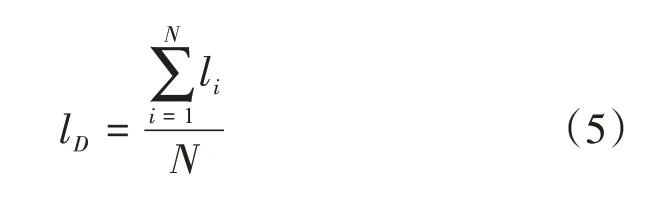
式(5)中:各变量含义同前。
最后,计算出租车排队平均等待时间wD:

式(6)中:各变量含义同前。
对于M/M/C 排队模型,当整体服务强度小于1时,乘客的平均排队长度lX为:

式(7)中:ai为每辆出租车的服务强度,按式(8)计算;n为常数,取n=0,1,…,Gi-1;其余各变量含义同前。

排队中的平均等待时间wX为:

结合黎冬平等[17]的研究结果(调查问卷数据中有83.4%的乘客认为合理的排队时间不应超过10min),设定乘客期待排队时间wexcept=10min,作为出租车接续运输供需匹配度指标,分析枢纽内出租车高峰小时运能匹配情况,通过比较该指标与乘客实际排队时长的大小,判断出租车供需匹配关系是否协调。若wexcept大于实际排队时长,则表示供需匹配良好,反之表示供需匹配不佳。
2.3 供给不足条件下的供需匹配评价模型
当出租车供给不足时,到达出租车调度站的旅客需要等待出租车的到达,结合该情况下出租车到达时间间隔,确定旅客等待时间,根据式(10)对出租车服务效率进行修正,再应用SBC法(式(1)~式(9))重新确定旅客的平均排队时间。
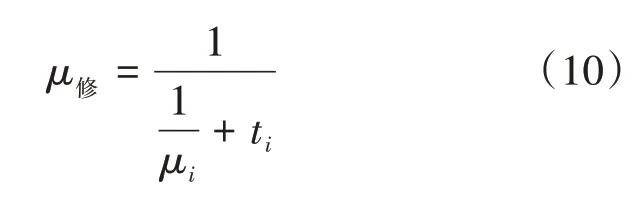
式(10)中:μ修为出租车不足时出租车服务效率(人/min);μi为出租车充足时服务效率;为乘客服务时间(min);ti为出租车到达间隔,即乘客等待出租车的时间(min)。
参照2.2 节所得符合乘客期待的排队时长wexcept,即出租车供需匹配度指标,通过比较该指标与乘客实际排队时长的大小,判断出租车供需匹配关系是否协调:若wexcept大于实际排队时长,则表示供需匹配良好,反之表示供需匹配度不佳。
3 出租车接续运输供需匹配评价案例分析
对外客运枢纽场站的客流时空数据分析表明,每周的周五、周日为对外客运枢纽旅客往返高峰日,接续运输需求和运力矛盾较为突出,易出现供需不匹配的情况。本文基于北京南站客流及运力数据,选取其出租车东侧调度站进行案例分析,对2020年6月12日(该日与常态化周五的列车抵达车次及分布无显著差异)的出租车供需匹配情况进行评价,并将计算得到的平均等待时间与实地测算的实际等待时间进行比较,以验证模型的准确性。
3.1 出租车接续运输客流特征分析
通过统计特定小时时段内抵达出租车排队区的乘客数,进行客流特征分析。北京南站出租车东侧调度站在2020 年6 月12 日7:00—23:59 的每小时出租车客流量如图2 所示,当日0:00—6:59无抵达车站的高铁列车;17:00—17:59 为当日出租车客流高峰时段,该时段抵达排队区乘坐出租车的总人数为782。夜间23:00—23:59时段,相比21:00—22:59 时段,乘坐出租车人数明显回升,达493 人,该时段北京南站轨道交通、常规公交结束运营,出租车、网约车、私家车等成为接续乘客的主要交通运输方式,供需矛盾客观上较为突出。
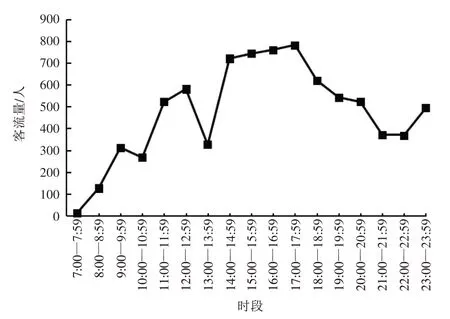
图2 北京南站出租车东侧调度站出租车客流量(2020年6月12日)
3.2 出租车充足条件下的供需匹配评价
依据图2,通过相关研究[18]及现场调查,在本案例分析中,确定北京南站出租车东侧调度站出租车的平均载客率等相关参数,其中服务台个数为2(即该调度站上车点每次会有2辆出租车同时服务,即存在2列出租车车队),平均载客率为1.8人/辆,车辆充足时的平均服务率为2.5人/min,由此计算北京南站出租车东侧调度站出租车运能匹配情况。
假设该站2020年6月12日高峰时段内出租车站的乘客到达间隔及出租车到站间隔服从泊松分布,且北京南站出租车东侧调度站晚高峰时段出租车平均载客人数为1.8人/辆,则单位时间内到达出租车站的乘客人数为:

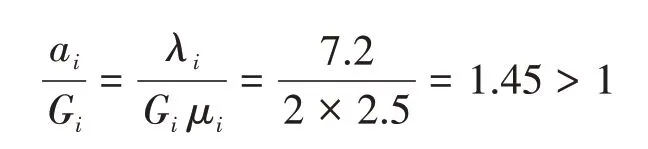
出租车整体服务强度大于1,根据式(1)~式(6),以1min作为时间间隔预估排队长度,则高峰小时内平均排队长度lD和平均等待时间wD分别为:
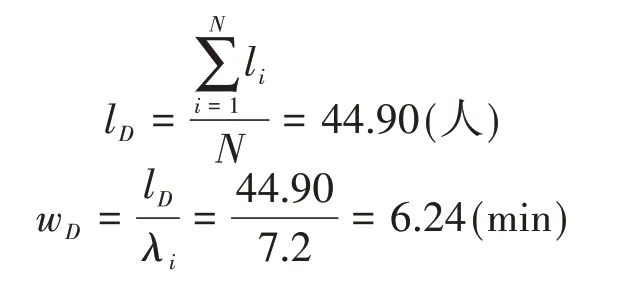
综上所述,乘客的平均排队长度约为45 人,平均等待时间为6.24min。基于实地测算,北京南站出租车东侧调度站高峰时段内的实际平均等待时间为6.86min,计算值与实际值相差0.62min,误差率为9.7%<10%,说明计算结果准确,模型可靠。根据2.2 节,已知北京南站东调度站出租车乘客期待排队时间wexcept=10min,而wD=6.24min 依据图2,假设夜间出租车供给相对不足,结合实际调查与相关研究结果[19],将出租车到达时间间隔设为2min,根据式(10),该站2020 年6月12日23:00—23:59时段内出租车服务效率为: 假设23:00—23:59 时段内出租车站的乘客到达时间间隔及出租车到站时间间隔服从泊松分布,且出租车平均载客人数为1.8 人/辆,则单位时间内到达出租车站的乘客人数为: 出租车整体服务强度为: 以1min作为时间间隔预估排队长度,高峰小时内平均排队长度lD和平均等待时间wD分别为: 综上所述,在出租车供给不足时,出租车的服务率仅为0.41,导致夜间出租车的整体服务强度大于1,乘客需要等待出租车到达,乘客的平均排队长度为69 人,平均等待时间为15.20min。基于实地测算,北京南站出租车东侧调度站夜间时段的实际平均等待时间为16.68min,计算值与实际值相差1.48min,误差率为8.9%<10%,说明计算结果相对准确,模型可靠。根据2.2 节调查结果,取北京南站东调度站出租车乘客期待排队时间wexcept=10min,wD=15.20min >wexcept,故该时段内北京南站东调度站出租车乘客的实际平均排队时间超过乘客期待的排队时间范围,其运能匹配程度较差,需要加强出租车接续运输运力保障。 因此,在实际应用中,可依托各站台的监测功能及现有数据平台,通过多种手段动态采集航班、列车班次及客流数据、出租车接续运输的调度与运力、客流数据,并基于多方数据,在枢纽组织与规划方面,合理有效地进行枢纽场站内部功能规划与系统设计,优化设施布局及各个功能设施或建筑空间布局,加强场站内的交通组织与联系。在运营调度方面,实时监测供需匹配情况,保障出租车供需匹配评价模型得以及时有效地运用,根据分级预警指标,实施不同情况下各接续运输方式运力调度的特定方案。在信息共享方面,建立接续运输协调运行保障基础数据库,完善信息共享体系,提升接续运输保障能力和服务效率。 为科学评价对外客运枢纽的出租车接续运输供需匹配情况,本文基于排队论模型,采用SBC方法,引入了出租车服务供需匹配指标,构建了基于乘客期望等候时间的出租车接续交通方式的供需匹配评价模型,然后以北京南站出租车东侧调度站作为研究对象开展案例分析,评价了该站2020 年6 月12 日高峰时段与夜间时段出租车的运能匹配情况,并将所求平均等待时间与调查的实际平均等待时间进行对比,发现模型评价结果准确、可靠。然而,受多模式交通数据不完备的限制,本文只开展了对外客运枢纽中出租车接续运输的相关供需匹配评价方法研究。现实中,公交、轨道交通等都是枢纽接续运输的主要交通方式,各自的供需匹配情况也会彼此影响,故未来有必要针对枢纽场站内各接续运输方式的供需匹配情况进行综合评价,从而为合理组织枢纽场站内各接续方式的运输与调度提供更全面的信息支撑,提高整个枢纽的换乘效率和保障能力。3.3 出租车不足条件下的供需匹配评价



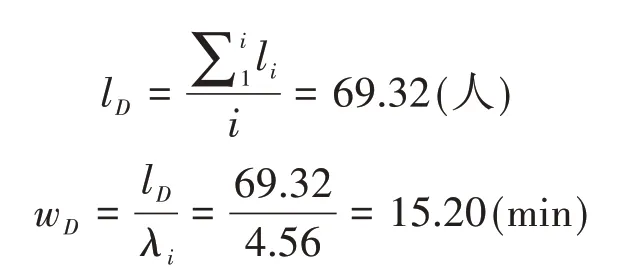
4 结语
