公交线网及发车频率同步优化研究

陈 巍，黄丹芮，吴 奇，



公交线网及发车频率同步优化研究

陈 巍1，黄丹芮2，吴 奇2，

（1. 重庆城市交通研究院有限责任公司，重庆 400020；2. 西南交通大学，交通运输与物流学院，成都 610031)

出行时间是从乘客角度评价公交系统合理性的重要指标，在规划层面出行时间主要与公交线网和发车频率设计有关。现有的研究主要是依据已有站点及规划线路数量首先确定公交线网方案，然后设计每条线路的发车频率，但将线网规划和发车频率分开设计导致最终得到的结果不是整体最优。据此，本文构建了公交线网及发车频率同步优化模型，在此基础上设计遗传算法实现模型求解，并引用一实际历史案例对公交线网及发车频率同步优化方法进行验证。结果表明，该方法能够为规划区域设计出乘客出行时间最小化的公交线网以及与公交线网相匹配的发车频率方案。

城市交通；同步优化；遗传算法；公交线网及发车频率；公交规划

0 引 言

乘客出行时间是衡量公交系统合理化的最重要指标[1]，对于站点布局确定的规划区域乘客出行时间主要包括两个部分：达到公交站点的等待时间和上车之后乘坐公交到达目的站点的在车行驶时间[1,2]。等待时间主要与线路发车频率有关，站点间的行驶时间与公交线网布局有关，如何确定最佳的线网布局及相应的发车频率是公交规划过程中的重要部分[3-5]。现有研究主要采用分阶段优化方式，对于如何根据出行需求来确定线网布局和发车频率，尚缺乏统一协调研究[6]。据此本文构建公交线网及发车频率同步优化模型并设计相应算法求解该问题。

1 问题描述

早期的公交线网规划没有考虑发车频率，主要是将直达最大化的线网布局作为最佳方案。如文献[7-9]以换乘最小化直达最大化为目标得到公交线网布局方案，但仅仅用可达性作为公交线网规划依据不能够完整体现出行者需求；文献[10]提出以出行时间设计公交线网，但文中虽然考虑了以时间成本为目标函数来优化公交线网，但在出行时间中线路发车频率是重要影响因子，文中缺乏线网布局和发车频率的同步优化。本文以出行时间为目标，构建公交线网及发车频率同步优化模型，并设计求解优于其他算法的遗传算法实现问题求解。

发车频率设计研究可以分为两个阶段，早期的发车频率是依据单条线路客流量，权衡车辆配备费用及乘客等待时间设计发车频率[11,12]，但依据单线路的发车频率设计方法忽略了公交线路在运营过程中线路之间相互影响关系。文献[13]提出公交线网发车频率设计应该考虑公交线路之间的相互关系，以公交线网为对象设计发车频率比单线路设计更加符合实际情况。文献[14,15]指出公交线网发车频率设计为NP-Hard问题，考虑问题复杂性设计了遗传算法实现了问题的求解。

现有的公交线网和发车频率设计分阶段进行。但出行时间与公交线网设计及发车频率都有关，文献[16]认为发车频率和线网同步设计更加合理，并基于已经形成的线路集，筛选线路组合成最优化方案。文献[16]中仍然是发车频率和线网分别进行优化，但考虑了两者解的组合进行优化，随着线网规模扩大，其可行线路数量呈指数增长，对于一定规模的城市，要找出组合优化解非常困难，工作量巨大。

根据上述分析，本文以出行时间最小化为目标构建公交线网与发车频率同步优化模型，并设计遗传算法实现问题求解。与现有的分阶段设计研究不同，本文采用线网与发车频率同步生成策略，能够实现公交线网与发车频率同步优化，适应于大规模线网设计。

2 模型构建

公交线网及线路发车频率同步优化问题是公交线网优化和发车频率优化问题的组合问题，目的是为了获取规划区域最佳线网布局及与线网中每条线路相匹配的发车频率。根据文献[17-19]相关研究，模型假设如下：

2.1 模型假设

（1）规划区域站点布局及规划线路条数已知；

（2）乘客的到达随机；

（3）乘客平均等待时间为相邻两辆车间隔时间的一半；

（4）乘客优先选择直达线路；

（5）车辆停靠时间忽略不计；

（6）乘客出行线路选择是基于最短路原则；

（7）乘客优先选择有直达线路的出行方案。

2.2 公交线网及发车频率同步优化模型构建

根据相关概念可知，乘客出行时间最小化是公交线网及发车频率设计的最主要目标。依据文献[16]研究，乘客出行时间由到站等待时间和在车运行时间构成，公交线网和发车频率同步优化比分阶段设计公交线网和发车频率更加合理，本文构建公交线网和发车频率同步优化模型如下：

2.2.1 目标函数

（1）公交到站等待时间模型构建

等待时间是指乘客到站后等待任意一辆覆盖乘客出行OD的车辆。当假设乘客服从随机到达规律时，根据文献[1]可知，乘客平均等待时间为：

总的等待时间计算如下：

（2）在车运行时间模型构建

在车运行时间是指，乘客从起始公交车站上车后到目的公交站点下车期间公交运行时间，与起始站点和终点站点的公交线路长度及公交本身速度有关。乘客总的公交运行时间为：

（3）公交线网与发车频率同步优化模型

根据上述分析可知，目标函数为

2.2.2 约束条件p

根据文献[1]中公交线网模型约束和发车频率相关研究，结合公交线网与发车频率同步优化实际问题，构建约束条件如下：

3 公交线网及发车频率同步优化模型求解算法

公交线网及发车频率同步优化本身属于NP-Hard问题，传统的算法很难得到整个规划区域的最佳线网布局及相应发车频率的方案。针对该问题，有关研究表明利用遗传算法迭代优化的性质能够很好求解该问题。据此本文设计遗传算法求解该问题，遗传算法求解流程如图1所示。

图1 遗传算法求解流程图

Step1：通过前期工作确定规划区域站点数量、线路条数、站点间距离等相关数据，作为数据输入；

Step3：依据乘客优先选择直达线路及以最短路出行条件的假设原则，分配乘客客流；

Step4：根据公式（4）计算种群内每个公交线网的适应度值；

Step5：对算法是否停止做出判断,如果停止则输出优化结果，如果未停止则进行下一步；

Step6：依据选择规则和设定的交叉变异概率,选择公交线网进行相关的交叉变异操作，得到与原种群规模一致的新的公交线网和相应发车频率方案；

Step7：对公交线网子代及其父代按目标函数值大小进行排序，取目标函数值大的作为新的种群，并转至Step3。

4 算例分析

（1）算例条件说明

该方法将应用至一个如图2所示的包含8个节点的线网，其中站点间的运行时间以及站点间客流OD如表1所示，该算例与文献[1]一致。本算例中规划线路数量为12条，发车间隔最小为4 min，最大发车间隔为20 min，每条线路最少站点数为3，最大站点数为4，整个线网车辆配备总数量不超过120辆。

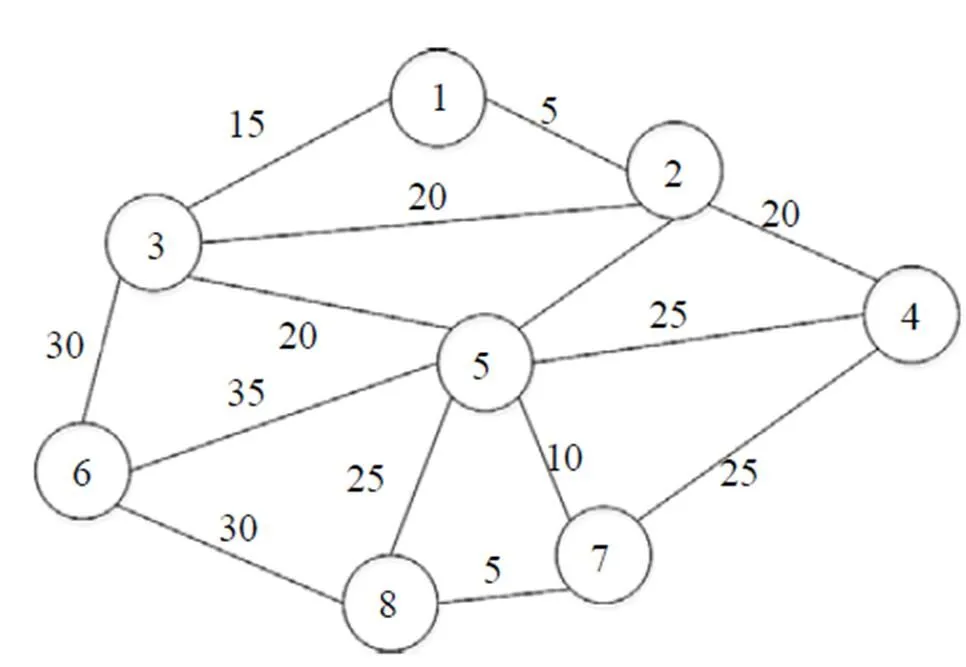
图2 算例站点及道路布局图

表1 公交站点OD矩阵表

（2）将算例的已知条件代入本文构建的公交线网和发车频率同步优化模型，运用Matlab编写模型求解，求得最终结果如见表2：

表2 线路及发车频率优化结果

Tab.2 Optimized results

（3）结果分析

① 通过对模型求解得到了公交线网与发车频率同步最优化方案，最终得到如表2所示的12条线路的具体线路方案以及每条线路相应的发车间隔，基于最短路以及优先选择直达出行的原则，满足整个出行需求总的出行时间为439 172 min。

② 通过公交线网及发车频率同步优化模型及相应的算法，可以同时得到等待时间最小化的公交线网及相应的发车频率方案，将以往分阶段进行的公交线网优化及发车频率优化结合进行整体优化，得到整体最优解，防止分阶段进行产生局部最优解。

5 结 论

不同于以往对公交线网及发车频率分阶段优化，本文结合乘客出行时间与公交线网和发车频率的设计关系，构建公交线网及发车频率同步优化模型，依据模型设计相应求解算法，实现了公交线网及发车频率同步优化，并结合历史案例，验证了本方法的可行性和合理性。

[1] CEDER A. Public transit planning and operation: theory, modeling and practice[M]. Elsevier: Butterworth Heinemann, 2007.

[2] SZETO W Y, WU Y. A simultaneous bus route design and frequency setting problem for Tin Shui Wai, Hong Kong[J]. European Journal of Operational Research, 2011, 209(2): 141-155.

[3] NIKOLIĆ M, TEODOROVIĆ D. A simultaneous transit network design and frequency setting: computing with bees[J]. Expert Systems with Applications, 2014, 41(16): 7200-7209.

[4] LI Y, XU W, HE S. Expected value model for optimizing the multiple bus headways[J]. Applied Mathematics and Computation, 2013, 219(11): 5849-5861.

[5] VERBAS İ Ö, MAHMASSANI H S. Exploring trade-offs in frequency allocation in a transit network using bus route patterns: methodology and application to large-scale urban systems[J]. Transportation Research Part B: Methodological, 2015, 81(1): 577-595.

[6] ARBEX R O, CUNHA C B D. Efficient transit network design and frequencies setting multi-objective optimizationby alternating objective genetic algorithm[J]. Transportation Research Part B: Methodological, 2015, 81(1): 355-376.

[7] BAAJ M H, MAHMASSANI H S. An aI‐based approach for transit route system planning and design[J]. Journal of Advanced Transportation, 1991, 25(2): 187-209.

[8] BAAJ M H, MAHMASSANI H S. Hybrid route generation heuristic algorithm for the design of transit networks[J]. Transportation Research Part C: Emerging Technologies, 1995, 3(1): 31-50.

[9] NES V, HAMERSLAG R, IMMERS R. Design of public transport networks[J]. Mathematical Models, 1988.

[10] MARTÍNEZ H, MAUTTONE A, URQUHART M E. Frequency optimization in public transportation systems: formulation and metaheuristic approach[J]. European Journal of Operational Research, 2014, 236(1): 27-36.

[11] NEWELL G F. Dispatching policies for a transportation route[J]. Transportation Science, 1971, 5(1): 91-105.

[12] SALZBORN F J M. Optimum bus scheduling[J]. Transportation Science, 1972, 6(2): 137-148.

[13] HAN A F, WILSON N H M. The allocation of buses in heavily utilized networks with overlapping routes[J]. Transportation Research Part B: Methodological, 1982, 16(3): 221-232.

[14] LI Y, XU W, HE S. Expected value model for optimizing the multiple bus headways[J]. Applied Mathematics and Computation, 2013, 219(11): 5849-5861.

[15] WU J, SONG R, WANG Y, et al. Modeling the coordinated operation between bus rapid transit and bus[J]. Mathematical Problems in Engineering, 2015, 2015(1): 1-7.

[16] OUYANG Y, NOURBAKHSH S M, CASSIDY M J. Continuum approximation approach to bus network design under spatially heterogeneous demand[J]. Transportation Research Part B: Methodological, 2014, 68: 333-344.

[17] KIM M E, SCHONFELD P. Integration of conventional and flexible bus services with timed transfers[J]. Transportation Research Part B: Methodological, 2014, 68(1): 76-97.

[18] AMIRIPOUR S M M, CEDER A A, MOHAYMANY A S. Designing large-scale bus network with seasonal variations of demand[J]. Transportation Research Part C: Emerging Technologies, 2014, 48(1): 322-338.

[19] CHEW J S C, LEE L S, SEOW H V. Genetic algorithm for biobjective urban transit routing problem[J]. Journal of Applied Mathematics, 2013, 2013(1): 1-15.

（中文编辑：李愈）（英文审改：孙湛博）

Simultaneous Optimization of Transit Network and Frequency

CHEN Wei1，HUANG Dan-rui2，WU Qi2

（1. Chongqing Urban Transportation Research Institute Co. Ltd, Chongqing 400020, China;2. School of Transportation and Logistics, Southwest Jiaotong University, Chengdu 610031, China）

Passengertravel time is an important evaluation index for public transportation system. At the planning level, the design of transit network and frequency are mainly based on passenger travel time. Existing research usually conducts the transit network design and timetabling through separate tasks. This scheme, however, usually leads to sub-optimal conditions. This paper constructs a model to simultaneously optimize transit network and timetabling. Genetic algorithm-based solution approach is then proposed. The feasibility of the model is tested using a real world case.

urban traffic; simultaneous optimization; genetic algorithm; transit network and frequency; transit planning

1672-4747（2018）02-0112-05

U491

A

10.3969/j.issn.1672-4747.2018.02.018

2017-03-13

陈巍（1989—），男，汉族，四川广安人，硕士，重庆城市交通研究院有限责任公司交通规划师，研究方向为公共交通规划。

黄丹芮（1994—），女，汉族，四川乐山人，西南交通大学交通运输与物流学院硕士研究生。

陈巍，黄丹芮，吴奇. 公交线网及发车频率同步优化研究[J]. 交通运输工程与信息学报, 2018, 16(2): 112-116.