城市近郊区轨道社区的接驳公交线路优化

惠煌，马健霄，冯 昕，朱震军，许馨方

（南京林业大学 汽车与交通工程学院，江苏 南京 210037）

0 引言

在城市近郊区，轨道交通的线网密度较小，站点间距较大，该区域内存在较大的轨道交通服务空白，居民通过自行车、步行等方式接驳效率较低，依靠轨道站点通勤受到距离、费用、换乘次数等因素的制约。本文的轨道社区是指分布在轨道站点周围1～3km，围绕轨道站点开发建设，受其直接服务，内部有成熟的支路网将各个小区紧密连接在一起，居民通勤出行主要依靠轨道站点的连绵成片的居住片区。大型轨道社区的出行需求量大且集中，出入口位置影响着居民出行。随着轨道交通网络的发展，大量的轨道站点被轨道社区包围，轨道站点的服务范围不再局限于轨道交通线路一侧的居住区。接驳公交作为城市公共交通系统的重要组成部分，能够填补轨道交通的服务缺口，满足轨道社区居民通勤出行需求。

城市近郊区公交线路通常服务于中心城区外围，交通密度相对较低，许多乘客出行较为集中且有一个共同的目的地[1]。现有研究较多关注公交的运营特点和服务目的，分析城市接驳公交的客流特性[2-5]。Jaehyun等[6]研究发现，出行需多次换乘时，通勤者选择公交的概率会降低。管娜娜等[7]认为，轨道站点周边居民主要依靠社区公交满足出行需求。张思林、武倩楠等[8-9]研究认为，公交站点可以满足相邻需求点的乘客出行需求，离公交站点较近的居民更有可能选择公交出行，从而建立模型，通过客流预测、数据分析优化了发车间隔和站点布设方案，降低了公交运营成本，提高了公交运行效率，为后续优化公交线路、提高乘客换乘便捷性奠定了基础。构建模型是线路优化的关键步骤，孙杨等[10]以轨道交通与公交线路一体化为研究对象，构建公交线网优化调整的多目标规划模型，从而调整常规公交线路走向，优化线路的运营参数。Zheng等[11]引入需求系数建立了接驳公交路线优化模型。在模型求解方面，既往研究多直接采用启发式算法[12-15]。

既有研究较多关注多个公交站点接驳一个轨道站点（多对一）的情况，较少针对两条及以上轨道交通线路相交的城市近郊区，研究多个公交站点接驳多个轨道站点（多对多）的线路优化问题。本文以南京近郊区为例，构建双层规划模型，应用遗传算法对模型求解，优化接驳公交线路，旨在充分利用现有公交站点及轨道社区的出入口位置的前提下提高居民短距离出行的便捷度。

1 轨道社区接驳公交的特性及存在的问题

在城市近郊区，轨道交通线网密度和可达性较低，居民通过自行车或步行接驳轨道站点花费时间较多，而且在换乘站点周围的轨道社区居民会根据各自的偏好选择不同的轨道站点出行。出行目的决定客流的流向，掌握接驳公交服务对象的出行生成和吸引源，有利于明确接驳公交线路的走向。接驳公交乘客出行目的多样化，主要包括上班、购物、上学等。以通勤为目的的居民是接驳公交的主要客源，且大多数乘客需要经过换乘到达轨道站点。轨道社区居民出行和返程时间主要集中在早晚高峰，其余时段较为平缓。为减少通勤乘客的等待时间，早晚高峰时段发车间隔时间应小于平峰时段。

多对多的轨道社区接驳公交线路可以满足轨道社区居民选择不同站点出行的需要，其线路优化涉及乘客、运营者和政府等多个主体。接驳公交现存问题的相关调查结果如图1所示。

图1 接驳公交系统存在的主要问题

从乘客的角度看，接驳公交线路设计不合理是目前最主要的问题。公交站点与轨道站点的位置、候车时间、换乘时间等因素影响接驳公交线路的优化。乘客可接受的最长候车时间为6～10min。此外，乘客可接受的候车时间还与出行距离有关：距离轨道站点1～3km 时，居民倾向于乘坐公共汽车；距离轨道站点不足1km 时，居民则更倾向于步行。运营者对客流量和发车频率关注度较高，发车频率和线路长度会影响公交公司运营成本，乘客数量则直接关系到公交公司的收入。发车频率越高，乘客的满意度就越高，但车辆满载率会随之降低，公交公司收入将减少。因此，优化接驳公交线路需要充分了解客流特征，在保证候车时间尽可能短的前提下，提高公交车辆的满载率。

2 模型建立

双层规划模型是递阶型结构的系统优化问题，上层决策者先做出决策，下层决策者再根据上层的决策做出决策，以实现下层目标，将决策返回到上层，然后上层决策者再根据下层决策做出总体最优决策。城市公共交通系统规划符合双层规划的特点，公交公司为公交用户提供公交线路和基础设施，居民的出行需求又会影响公交公司的线路设置，既能体现公交公司和公交乘客的利益，又能体现两者之间的相互作用。当前，随着我国个体机动化水平日益提高，公共交通发展面临着严峻挑战。因此，提高运营效率、合理配置资源、完善运营组织尤为重要。而完善运营组织首先就要从乘客的出行成本和公交的运营成本出发，在有限的条件下达到财务平衡，实现可持续发展。乘客出行成本主要包括票价及时间成本。公交的运营成本主要涉及固定成本及运营成本，其中人员工资及工资性支出成本在公交运营成本中的占比超过50%，需要重点考虑，通过合理定编，控制劳动力投入，提高管理效能，最大程度降低人力资源的无效损耗，从而降低公交运行成本。所以，接驳公交线路的优化，应在满足居民出行需求的同时，保证成本最低。本文以出行成本和运营成本最小作为上层模型，乘客直达率最大作为下层模型。

（1）上层规划模型

上层规划模型的目标是乘客的出行成本和公交的运营成本之和最小。

式（1）中：C为总成本；C1为乘客出行成本；C2为公交运营成本；η1和η2为权重系数。

乘客出行成本C1包括：从出发地到公交站点的时间成本、在公交站点的候车时间成本、在车的时间成本和从公交站点到轨道站点的时间成本。其计算方法如下：

式（2）中：α为乘客单位时间成本；N为公交站点数量；i,j为公交站点序号；Dij为公交站点i与公交站点j之间的乘客流量；ρ1,ρ2,ρ3,ρ4均为时间权重；xij为该公交线路是否经过弧（i,j）的判定因子；s为公交线路起点；t为公交线路终点；若s,t之间有公交线路且经过弧（i,j），则xij=1，否则xij=0；t1为出发地到公交站点的时间；t2为候车时间；t3为在车时间；t4为下车后到轨道站点的时间；R1为乘客的平均步行距离；v1为乘客的平均步行速度；H0为发车间隔；v2为公交的平均行驶速度；L为乘客的平均乘车距离，按式（3）计算；其他参数含义同前。

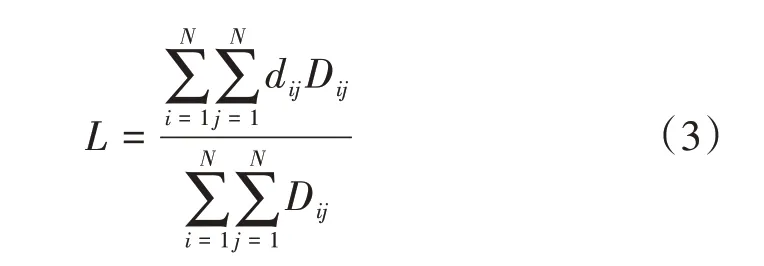
式（3）中：dij为公交站点i到公交站点j间的距离；其他参数含义同前。

公交运营成本C2包括：公交车辆的固定成本、运营成本和公交站点的固定成本。其计算方法如下：

式（4）中：lst为公交线路从起点到终点的长度，按式（5）计算；λ为公交线路一天内总运营次数；Fq为公交车每千米的运营成本；μ为公交线路运力配置；Fp为公交车的固定成本；为s,t之间是否有公交线路且在i站点停留的判定因子，若s,t之间有公交线路且在i站点停留，则=1，否则=0；ei为站点i作为接驳公交停车站点一天的固定费用；其他参数含义同前。

式（5）中：所有参数含义同前。

综上所述，上层规划模型为：

（2）上层规划模型约束条件

①线路长度约束（ls）t：公交线路的长度影响乘客的出行时间和换乘次数，若线路过短，会降低公交线路的覆盖率；若线路过长，会增加乘客出行时间，影响公交运营效率。该约束条件表示为：

②发车频率约束（f）：发车频率影响居民的出行时间和公交公司的运营成本。该约束条件表示为：

③公交站点数量约束（W）：公交线路站点设置过少，公交公司的收入随之减少；公交线路站点设置过多，乘客的出行时间随之增加。该约束条件表示为：

（3）下层规划模型

下层规划模型的目标函数是乘客直达率最大。乘客直达率Z为直达客流量与公交需求之比：

3 算法求解

双层规划模型属于非线性模型，求解较复杂且解的正确性难以检验，通常只能得到局部最优解，一般采用启发式算法求解。在公交线路的优化中，遗传算法有较大优势，其以概率为基础，从一个面开始随机搜索，而且运算简单、收敛速度快，是一种基于自然遗传机制和自然选择原理的搜索优化算法。上层随机给出初始公交线路，下层根据初始公交线路计算乘客直达率，将下层计算出的乘客直达率返回上层，求解上层目标，以上层目标作为整体目标开始迭代，直至满足迭代的终止条件。

具体步骤为：

（1）选择合适的种群规模M、迭代总数gmax、交叉概率Pc和变异概率Pm；

（2）进行二进制编码，产生初始接驳公交线路；

（3）计算每条接驳公交线路的适应度函数值并排序；

（4）根据适应度函数值选择是否遗传，淘汰适应度函数值低的；

（5）根据概率进行交叉、变异，生成新的接驳公交线路；

（6）若g=gmax，则进入步骤（7）；否则，令g=g+1，返回步骤（3）；

（7）若N=vub，则终止算法；否则，令N=N+1，返回步骤（1）。

4 案例分析

4.1 研究区域

以南京市中华门站和安德门站轨道社区为例，研究接驳公交线路优化问题。轨道站点和公交站点分布如图2 所示，通过调查获取各公交站点间的出行交通量，如表1 所示。中华门站位于地铁1 号线上，共有4 个出入口，分别通往雨花西路和集合村路。安德门站是地铁1 号线与10 号线的换乘站，设有6 个出入口，通向小行路和安德门大街，并设有公交枢纽站。在安德门站和中华门站周围分布着大量的轨道社区，通勤出行需求集中，但与轨道站点的距离、出行成本、公交效率等因素制约着轨道社区居民选择轨道交通出行。

表1 公交站点间客流量表 单位：人/h

图2 轨道站点和公交站点分布图

4.2 参数标定

研究区域设置各参数为：η1=1,η2=6,λ=50,μ=6,ρ1=ρ2=ρ3=ρ4=0.25,R1=R2=300,em=1.5,α=0.2,v1=1.5m/s,v2=15km/h,H0=10min,2.5km≤lst≤5.0km,L=2.9km,5≤W≤15,f=12 对/h。每辆公交车的成本为25万元，公交车使用年限为10年，天然气的消耗量为0.34m3/km，天然气的价格为4.4 元/m3，公交站点的建造成本为5 000 元/个。Fp=250000/(365×10)≈70,Fq=34×4.4/100≈1.5,ei=5000/(365×3)≈4.6。应用遗传算法求解，设置种群规模为50，迭代次数为100，交叉概率为0.8，变异概率为0.1。

4.3 线路优化

本次线路优化的遗传算法迭代过程如图3 所示。可以看到，迭代至第65代时适应度值趋于平稳，模型以及算法有效适用。该案例的网络较为简单，可以随机产生初始值，从而得到最优解。当网络较为复杂时，初始值对解的影响较大，随机产生初始值可能陷入局部最优解，因此可以人工赋较优的初始值。

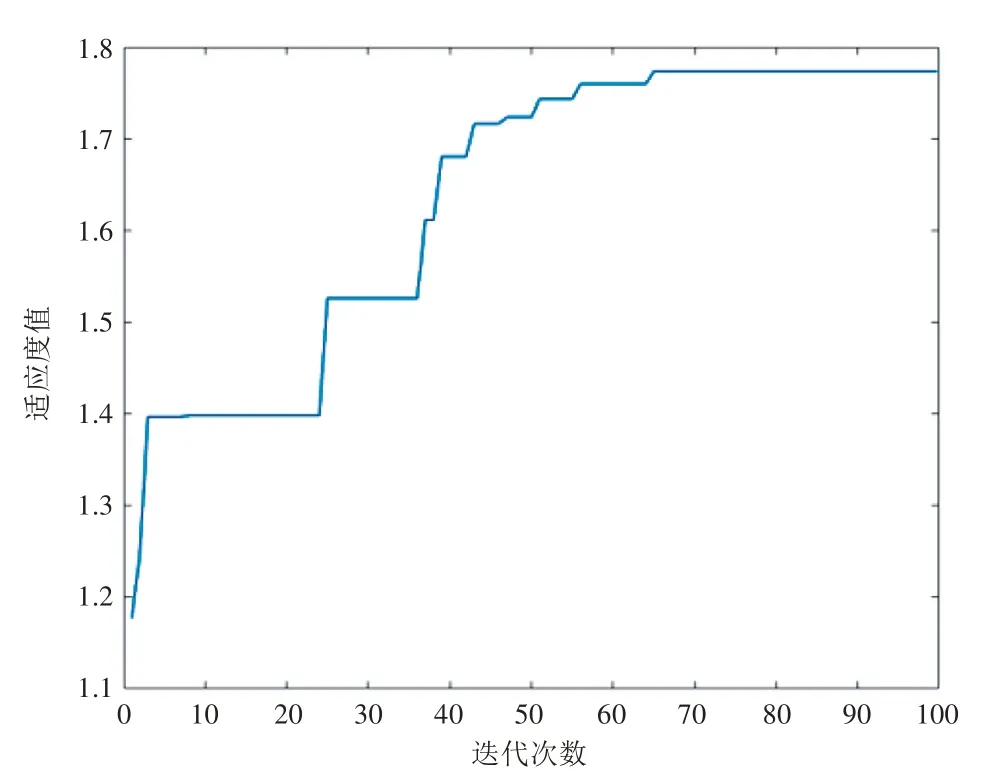
图3 遗传算法迭代过程图

综合考虑模型最优解选择最优方案，如图4所示，算法的最终结果为中华门站和安德门站优化了两条公交线路（接驳公交线路1 和接驳公交线路2），解决了多对多的接驳公交线路优化问题。线路1和线路2的长度分别为3.1km和4.8km，平均长度为3.95km。接驳公交线路1 和接驳公交线路2 分别有9 个、15 个公交站点，平均站间距为359m，满足了接驳公交的功能定位。线路涵盖两个轨道站点，基本覆盖了区域内的常规公交站点。建模求解得出，线路没有涉及的西云村和能仁里二村，现有常规公交线路较多，其中能仁里二村共有8 条常规公交线路，满足了周围轨道社区居民的出行需求，居民通过步行到达相邻站点乘坐接驳公交较为方便。

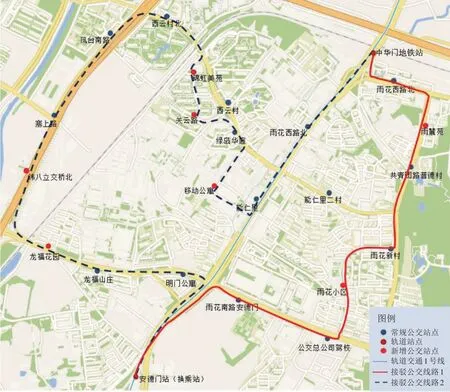
图4 接驳公交线路优化图

接驳公交线路利用现有站点，减少了建设成本，但有些站点间距较大，轨道社区居民需要长距离步行到达站点。考虑轨道社区出入口位置和居民出行需求，为更好地服务站点周边居民出行，减少步行距离，缩短接驳公交站间距，新增雨麓苑、雨花小区、龙福山庄等7 个接驳公交站点。线路在保证公交运营成本和乘客出行成本之和最小的情况下，乘客直达率较大，如表2所示。

表2 模型最优解

5 结语

本文分析了城市近郊区轨道社区接驳公交的特性，构建了轨道社区公交接驳线路优化模型，应用遗传算法求解。以中华门站和安德门站为实例，以出行成本和运营成本最小化、乘客直达率最大化为目标，求解得到两条多对多的轨道社区接驳公交线路。线路的优化充分利用了区域的常规公交站点，为缩短公交站间距、满足居民出行偏好、减少步行距离，新增了7个接驳公交站点。线路没有通过的公交站点，借助现有常规公交可以较好地满足居民的出行需求。

本文的接驳公交线路优化仅衔接了两个轨道站点，随着城市近郊区轨道交通网络逐渐成熟，接驳模式更加多样化，可进一步考虑在成网条件下分析接驳公交客流出行特征和时空分布特征，优化设计接驳公交线路，以衔接轨道交通线网上更多的轨道站点。在下一阶段研究中，构建模型时可以根据线网结构、公交运营效率等实际情况，加入更多道路和车辆参数；考虑低碳出行，可以将碳排放的相关参数加入，以完善模型。