弧边内凹蜂窝负泊松比结构的面内冲击动力学数值研究

尤泽华，肖俊华

(1. 燕山大学工程力学系，秦皇岛 066004；2. 燕山大学河北省重型装备与大型结构力学可靠性重点实验室，秦皇岛 066004)

负泊松比材料由周期排列的胞元构成，受到冲击时各胞元向载荷冲击点集中，从而使材料的抗压能力得到提升，材料具有高抗压性能[1−2]。传统材料(非负泊松比材料)受到纵向冲击时，材料横向发生膨胀，材料的抗压性能较低。同时，负泊松比多胞材料含有许多空隙，在受到外载时材料容易产生大的变形，从而具有较高的能量吸收效果[3−4]。负泊松比多胞材料除了具有良好的力学性能，胞元之间的空隙使得其具有较低的结构密度。负泊松比材料的优良力学性能使其广泛应用于实际工程中，例如：利用其高剪切模量可以作为汽车工业中的弹性座椅和建筑工程中的路面材料等[5]；利用其高抗压性能可以制作飞机机翼的纤维增强复合材料、金属泡沫、飞机涡轮喷气发动机的叶片等[6]；利用其负泊松比特点可以作为传感器[7]和过滤器[8]的制作材料；利用其轻质特点可以制作新型的作战服、人体防护装备、防弹衣等[9]。

负泊松比材料的胞元具有内凹多边形几何结构，主要有蜂窝六边形内凹结构、内凹三角形结构、星形结构等，之后又扩展出旋转刚体结构、手性结构、穿孔板结构、结点-纤维结构[1]。GIBSON和ASBBY[10]最早设计出以内凹六边形为胞元周期结构的负泊松比蜂窝材料，该材料受拉时通过肋骨位移变形获得与受力垂直方向上的膨胀，其泊松比受胞元的内凹角度、肋骨尺寸等因素影响，当胞元内凹角度不够大时，材料不具有负泊松比特性。SMITH 等[11]通过观察负泊松比泡沫材料在受力过程中的胞元变形，仿照轴对称胞元的肋骨结构去掉一定比例肋骨，建立了一种新型的负泊松比泡沫材料。该模型称为缺失肋模型，它不改变胞元内部的肋角，而将肋骨选择性去除。与原模型相比这种材料的负泊松比效应不再借助于凹角的胞元变形，而是胞元在受力之后产生旋转从而产生负泊松比效应。HOU 等[12]通过将内凹三角形孔隙随机嵌于平面材料中得到负泊松比特性，讨论了随机夹杂度与泊松比之间的关系。

常见的二维负泊松比结构有多边形内凹结构和手性结构，其中多边形内凹结构主要有三角形内凹结构、星形内凹结构和多边形内凹结构等[13−14]。蒋伟等[15]对传统的负泊松比结构单元进行再设计，提出一种新型的环形结构，随后沈建邦和肖俊华[16]在该结构的基础上提出可变弧角弧边负泊松比蜂窝结构。王彦斌和刘海涛[17]提出一种可变曲率内凹曲边负泊松比结构，并分析了结构的力学性能与结构参数之间的关系与动力学冲击下的力学性能。TAYLOR 等[18]研究了正交椭圆孔隙材料的泊松比与孔隙长径的关系。WANG 等[19]通过在基中制作特定排列的类花生型孔隙提出一种新型的负泊松比材料。吉美娟等[20]通过建立纸蜂窝结构单面冲击和双面冲击模型，探究了结构的动力响应、变形模式和缓冲吸能特性。马芳武等[21]应用LS-DYNA模拟了不同冲击倾角和冲击速度下内凹三角形负泊松比材料的面内变形模态和动力响应。郭春霞等[22]对正弦负泊松比蜂窝梁进行了平面三点弯曲实验研究，分析了相同质量时传统蜂窝梁和负泊松比蜂窝梁在面内的弯曲破坏模式和吸能效果。张权等[23]数值研究了面内冲击载荷作用时星形梯度负泊松比蜂窝结构的动态响应，探讨了冲击速度、厚度梯度、角度梯度对结构变形模式、动态响应、能量吸收特性的影响。王梁和刘海涛[24]将星型和内凹六边形结合设计出一种新型内凹蜂窝结构，计算了结构的相对密度并数值模拟了轴向拉伸变形。魏路路等[25]结合负泊松比内凹六边形结构和负泊松比手性结构，设计出一种内凹-反手性结构，研究了结构的抗冲击性能。严效男等[26]分析了热塑性聚氨酯弹性体蜂窝结构的压缩过程，探讨了胞元凹角、宽度和壁厚对结构的力学性能和能量吸收特性的影响。姚永永等[27]数值研究了传统内凹六边形结构的双向冲击行为，探讨了不同冲击速度时结构变形模式、动力响应曲线和能量吸收特性。刘海涛等[28]将圆弧杆设计于传统星形结构，利用能量法和数值模拟讨论了结构参数与等效泊松比和等效弹性模量之间的关系。

目前有关胞元为弧边结构负泊松比蜂窝材料的动力学性能研究非常有限，本文研究一种新型的二维弧形曲边内凹蜂窝结构，其胞元结构由全弧边组成，弧边角度可以改变从而可以控制材料的整体力学性能。在前期静力学性能分析[29]的基础上，利用数值方法研究了不同速度冲击时结构的面内变形失效模式，获得了结构的动力响应曲线，讨论了冲击速度、胞元弧边内角、压缩应变对结构能量吸收效率和平台应力的影响规律。该研究丰富了二维负泊松泊松比蜂窝材料的动力学分析，为该类结构的曲边胞元设计和表征提供了参考。

1 胞元与相对密度

图1 为可变弧角内凹弧边负泊松比蜂窝材料胞元示意图，其中：θ 为弧边内角；r为弧线半径；m为连接杆长度；h为弧线半弦长；杆件横截面为矩形；t为肋板厚度；d为面外厚度。蜂窝结构由胞元阵列构成。

相对密度是蜂窝结构的一项重要物理参数，定义为胞元的等效密度与制备材料密度的比值[30]：

式中： ρre为材料的相对密度； ρc为材料的等效密度； ρs为制备材料(本文取为铝合金)的密度。结构中连接杆只起连接作用，图1 胞元的相对密度可以通过图2 计算。

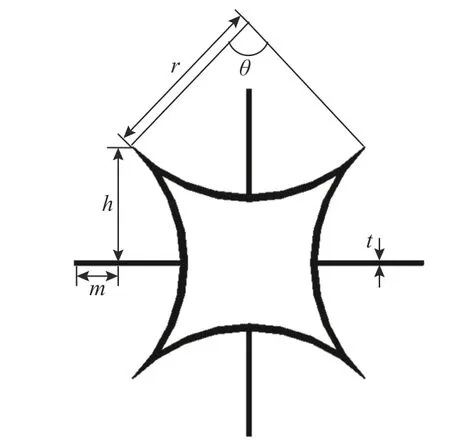
图1 弧边内凹蜂窝胞元[29]Fig. 1 Concave honeycomb cell with arc side[29]

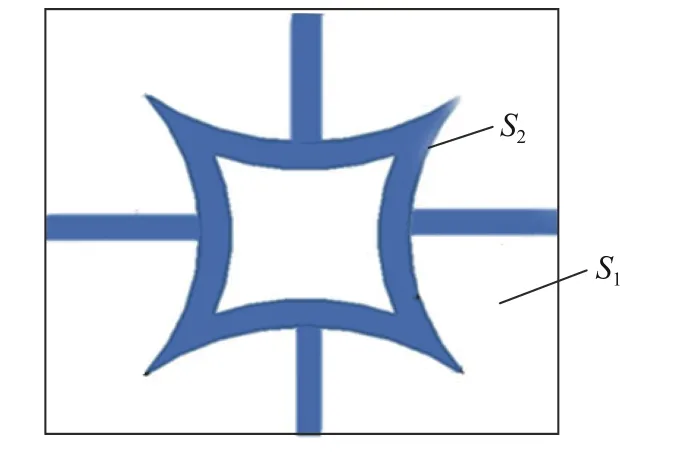
图2 相对密度计算示意图Fig. 2 Schematic diagram of relative density calculation

等效密度为制备材料所占胞元空间的比值与制备材料密度的乘积[30]：

式中：S1为胞元的二维面积(图2 中方框面积)；S2为材料几何形状在平面中的面积。将式(2)代入式(1)可得：

对于薄壁胞元，肋板厚度t比杆长和弧长小很多，S1和S2可按下列公式进行计算：

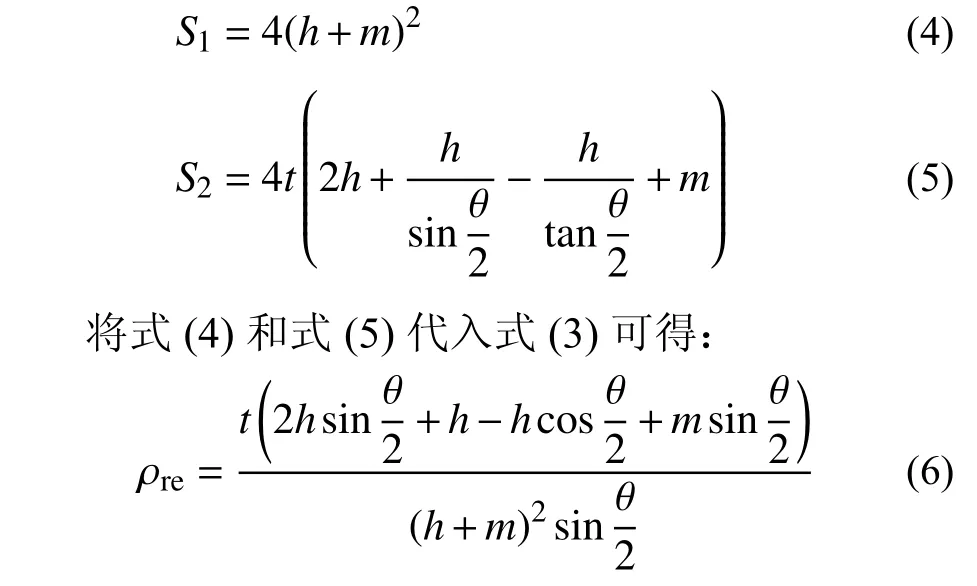
由图2 可以看出，当胞元厚度和弧边角度分别增加时，S2随之增加，而S1不变，材料的相对密度随着厚度和胞元弧边角度增大而增大。当材料受压缩冲击时，弧形肋边受到挤压导致曲率增大，胞元的弧形肋边弦长变小、弧度增加，两侧距离变小，结构整体向内部压缩后，其密实化程度逐渐提升，相对密度随之增加。

2 构建结构

利用二维单胞(图1)构建内凹蜂窝胞元结构模型(图3)，几何参数如下：胞元中心到胞元端部的高为30 mm，胞元之间连接杆伸长度为15 mm，弧边的内角分别取30°、45°、60°、75°和90°，整体结构模型由胞元按照19×19 方式阵列构成。

图3 冲击动力学结构模型Fig. 3 Structural model of impact dynamics

利用ABAQUS 研究面内冲击动力学性能。材料截面为长方形，截面高度为10 mm，厚度为1 mm，选用铝合金材料，具体参数见表1。构件置于两个板之间，两个板的属性为解析刚性板，使其在冲击过程中不发生变形并提高计算效率，顶部板和底部板分别与材料设置为绑定接触，接触面无摩擦。

表1 材料属性[31]Table 1 Material properties[31]

施加载荷和边界条件如图4 所示，顶端板冲击速度分别为7 m/s、21 m/s、35 m/s 和70 m/s，速度向下对结构进行冲击，底部为固定板，构件整体限制其Z方向(垂直于平面方向)位移。单元选择8 结点六面体单元，分析方式选择显式动力学分析，有限元分析时将顶部刚性板和底部刚性板分别与材料绑定，以避免在冲击过程中发生刚性板与材料之间发生穿透现象。

图4 边界条件和施加载荷示意图Fig. 4 Schematic diagram of boundary conditions and load conditions

3 冲击变形失效模式

图5 和图6 分别给出了冲击过程中弧角为30°和90°结构的局部变形模式。已有研究[29]表明：30°弧角胞元为正泊松比胞元，Y轴方向受到冲击时，胞元由内凹结构逐渐膨胀为外凸结构；而90°弧角胞元为负泊松比胞元，在冲击过程中逐渐向中心压缩。在变形带与顶板之间明显有一条弧形空隙带，结构中间的胞元发生扭转和位移，胞元发生扭曲变形，呈现出类星形的罗叠排列。比较图5 和图6 可以发现，在相同速度冲击下，胞元弧角较大的结构在冲击过程中密实化区域较薄，但是整体的变形范围较大。

图5 30°弧角胞元结构冲击变形模式Fig. 5 Impact deformation mode of 30 degree arc angle cellular structure

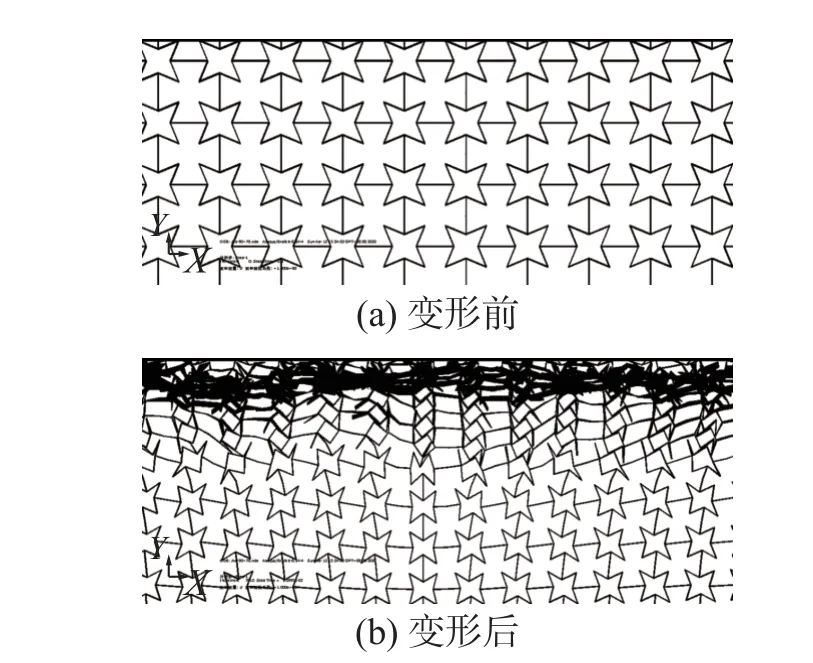
图6 90°弧角胞元结构冲击变形模式Fig. 6 Impact deformation mode of 90 degree arc angle cellular structure

图7 为弧角90°胞元在冲击过程中的变形模式。在变形初期胞元向几何中心压缩，材料的相对密度随之减小；随着变形增加，胞元上下连接杆错位，胞元受到扭矩的影响发生扭转变形，对角方向上的弧线夹角在扭转过程中相互贴合；随着变形继续增加，胞元在压力作用下各边贴合直至压缩成为片状。

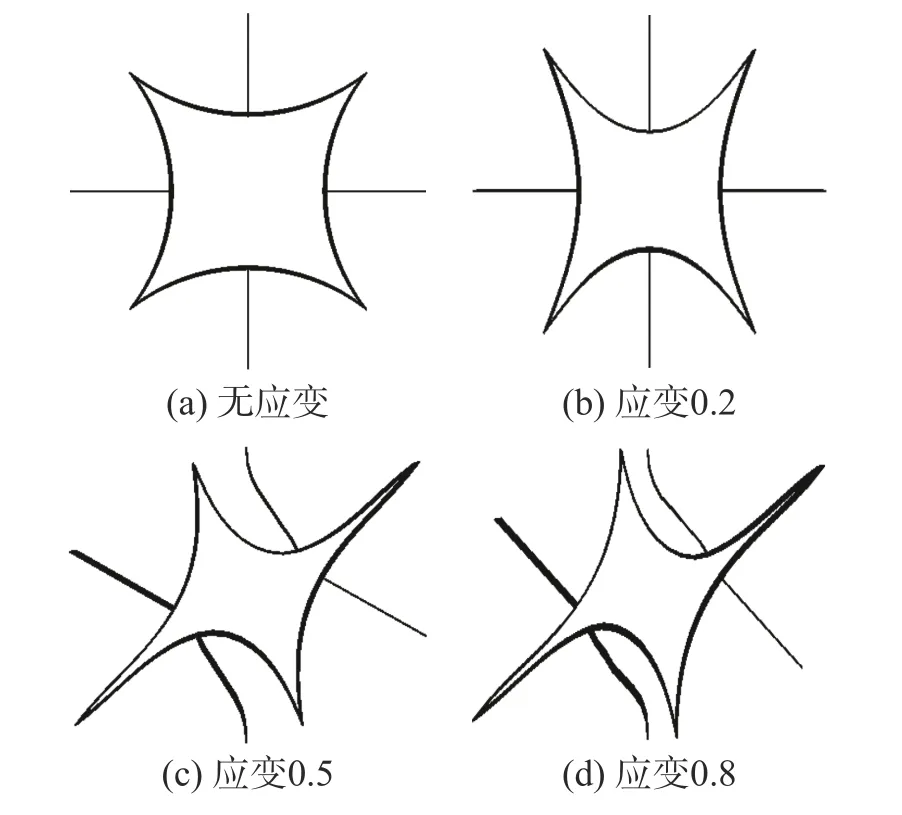
图7 胞元冲击变形模式Fig. 7 Deformation mode of the cell under impact

图8 分别为胞元弧形肋内角为30°和90°时整体结构在21 m/s 速度冲击下的变形模式。从图8中变形来看，当胞元弧角为30°时结构初始变形区域主要集中在上部，呈现V 字型；随着应变的增加，材料的中部开始进入密实化，上方V 字型变形区域开始扁平化，变形区域左右两侧位移有明显的向外增加的趋势，这与30°胞元结构的正泊松比力学性能相符合；在冲击过程后期，结构的变形区域开始压缩，变形主要集中在中间区域，上方与下方形成密实化的长方形区域带。当胞元弧角为90°时，在冲击过程初期，变形区域与30°弧角胞元结构大致相似，但是90°胞元结构的上方变形区域较大，且下方也有微小变形，材料中间区域出现向内位移趋势，这与90°胞元结构的负泊松比力学性能相符；随着变形的增加，结构上方区域变形保持不变，结构下方变形程度增加，变形方式与上方相似，中部保持向内挤压状态，整体呈现X 型。相对于30°弧角胞元结构来看，90°弧角胞元结构在冲击过程中的变形区域更大，由其负泊松比效应所表现出来的变形模式非常显著；对比30°弧角胞元结构，90°弧角胞元结构在整个冲击过程中变形更加平均，结构的密实化程度由于材料向内压缩也相对较高，因此，在冲击过程中的能量吸收效率比30°弧角胞元结构更好。

图8 结构的冲击变形模式Fig. 8 Impact deformation modes of the structure

4 动力响应曲线

图9 为不同弧边肋角时负泊松比结构受不同速度面内冲击时的应力-应变动力响应曲线，其中横坐标为名义应变，纵坐标为名义应力。

由图9 可以看出，结构在初始受冲击阶段名义应力快速增大，随后微弱降低并在某一数值范围内波动；最后结构进入密实化阶段，名义应力继续增加。冲击过程应力应变曲线可分为三个阶段：初始阶段、稳定阶段和锁定阶段。初始阶段的应力称为初始应力，稳定阶段的应力称为平台应力，锁定阶段的应变称为锁定应变。在初始阶段，结构中的大部分胞元处于向几何中心压缩的状态；之后结构进入稳定阶段，胞元在压缩与扭转双重作用下发生变形，成为类星形结构，此时结构中大部分胞元变形类似于图7(b)；最后结构进入锁定阶段，此时胞元接近压实状态，即处于图7(d)形变情况。从动力响应曲线可以看出，不同冲击速度下、相同应变情况时，结构中的名义应力随着冲击速度的增加而增大。弧边内角不同时，由于结构中胞元几何参数的变化，相对密度随弧边肋内角的增加而增大，结构受到冲击后，在产生相同的应变时其密实化程度相对于弧边内角较小的结构增大，因此结构进入密实化阶段时所对应的锁定应变较小，即：胞元的弧边角度越大，密实化程度越高，结构进入密实化时间越早，结构在密实化阶段所对应的应变越小。本文所得动力响应曲线不同于非负泊松比材料的结果[32]。

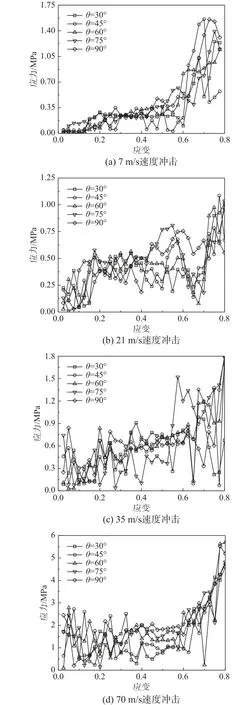
图9 不同冲击速度和弧角时应力-应变曲线Fig. 9 Stress-strain curves under different impact velocity and angle

结构在冲击载荷作用时，其能量吸收特性与平台应力和密实应变有很大关系，通常用材料的体能量吸收值进行评价，体能量吸收值、平台应力和锁定应变如下式[31]：

5 能量吸收率

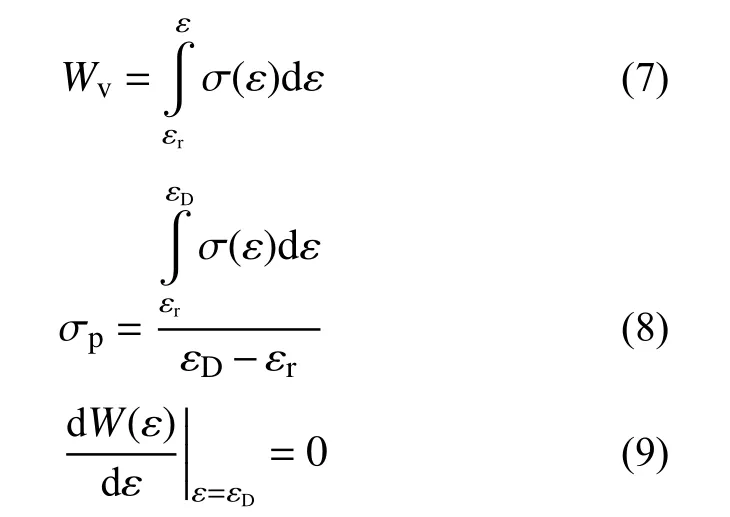
式中：Wv为材料在冲击过程中的体能量吸收值；εr为初始应变；εD为冲击过程中的锁定应变；σ(ε)为冲击过程的应力；σp为平台应力。

图10 为不同弧边肋内角结构在不同冲击速度下的能量吸收曲线。由图10 可知，当弧边肋内角一定时，低速冲击时结构在冲击前期吸能效果较低，在冲击中期阶段结构的能量曲线有较大增加，而后趋于能量稳定吸收状态。胞元弧边肋角度越大，体能量吸收值的显著增加阶段越早出现。当冲击速度一定时，在冲击初始阶段各结构间的能量吸收效率差距较小，而在冲击中后期阶段，结构的弧边肋角越大，其体能量吸收值越高；随着冲击速度的增加，这种变化逐渐变得不明显。高速冲击时，弧边肋角大的胞元结构其体能量吸收值在冲击初始阶段高于角度小的胞元结构，并在整体上呈现这种趋势。

图10 不同冲击速度和弧角时体能量吸收值曲线Fig. 10 Curves of volumetric energy absorptivity under different impact velocity and angle

6 平台应力

图11 为不同弧角结构的平台应力随冲击速度的变化曲线。已有研究[33]表明：多孔结构的平台应力与冲击速度大致成二次关系，这与本文结果相一致。图11 中显示：平台应力随冲击速度的增加迅速增大；冲击速度相同时，平台应力随弧角的增加而增大，冲击速度越大，不同弧角结构之间的平台应力差距越大，弧角为90°时结构的吸能效果最好。

图11 平台应力随冲击速度的变化曲线Fig. 11 Variation of platform stress with impact velocity

图12 为不同冲击速度时平台应力随曲边弧角的变化曲线。可以看出，同一冲击速度时结构的平台应力随弧角的增加而递增，且冲击速度越大这种现象越明显。这是由于结构的相对密度随着弧角的增加而增大，冲击过程中胞元弧角参数越大其结构所能承受的平台应力越高。对比图11 和图12 可以发现：平台应力受胞元弧角的影响较小，其值主要由冲击速度决定。

图12 平台应力随胞元弧角的变化曲线Fig. 12 Variation of platform stress with cell angle

7 结论

针对可变弧边内凹多胞蜂窝结构，利用数值手段研究了结构在冲击载荷作用下的变形失效模式、动力响应曲线、能量吸收特性和平台应力特征。研究发现：

(1) 冲击载荷作用下，结构胞元出现旋转位移，胞元发生扭曲变形，呈现出类星形的罗叠排列，在变形带与顶板之间有一条弧形空隙带。

(2) 胞元弧角较小时(文中以30°为例)，初始变形区域主要集中在上部呈现V 字型，随着应变的增加，材料中部开始进入密实化，上方V 字型变形区域开始扁平化，变形区域左右两侧有明显的向外位移，在冲击过程后期，结构的变形区域开始压缩，变形主要集中在中间区域。胞元弧角较大时(文中以90°为例)，冲击过程初期变形区域与低弧角胞元结构大致相似，随着变形增加，中部保持向内挤压状态，整体呈现X 型。

(3) 结构在初始受冲击阶段名义应力快速增大，随后微弱降低并在某一数值范围内波动；最后结构进入密实化阶段，名义应力继续增加。冲击过程应力-应变曲线可分为三个阶段：初始阶段、稳定阶段和锁定阶段。

(4) 低速冲击时结构在冲击前期吸能效果较低，在冲击中期阶段结构的能量曲线有较大增加，而后趋于能量稳定吸收状态。胞元弧边肋角度越大，体能量吸收值的显著增加阶段越早出现。冲击速度一定时，在冲击初始阶段各不同弧角结构间的能量吸收效率差距较小，而在冲击中后期阶段，结构的弧角越大其体能量吸收值越高。

(5) 平台应力随冲击速度的增加迅速增大；冲击速度一定时，平台应力随弧角的增加而递增，且冲击速度越大这种现象越明显。