基于SiPESC 平台的声子晶体能带结构分析算法研究及软件实现

姜殿恒，陈飙松，张 盛，李云鹏

(大连理工大学工业装备结构分析国家重点实验室，辽宁，大连 116024)

声子晶体是一类拥有带隙和缺陷态的特点的多介质周期性结构[1]。因其拥有带隙和缺陷态的特性，声子晶体可以阻隔与调控声波与弹性波在介质中的传播[2−3]，具有丰富的工程应用前景[4− 7]，可应用在各类减振降噪系统中[8−10]。声子晶体的能带结构分析可使用多种数值分析方法，诸如传递矩阵法、平面波展开法[11]、时域有限差分法[12]、多重散射理论[13−14]、有限元方法[15]等。各类方法的离散方式不同，数值计算手段不同，具有不同优势和劣势，从而适用于不同类型的分析问题。有限元方法具有不受问题维度及模型的几何特征所约束的特点，适用于各类能带结构分析问题，广泛应用于不同介质、不同周期性的声子晶体的能带结构分析。有限元方法计算量大、计算过程复杂，对于有限元方法的算法研究与软件开发是声子晶体仿真方法研究的核心问题。

声子晶体的有限元方法能带结构分析通常借助于诸如COMSOL、ABAQUS 等成熟的商用有限元软件[16]。此类软件没有直接的能带分析模块，研究人员通过设定多个模态分析步，分别调用商业软件中的广义特征值计算模块以完成声子晶体仿真功能。COMSOL 软件支持Hermitian 矩阵的广义特征值求解，只能定义网格的疏密性，无法进行独立单元的修改操作，因而无法使用该软件进行模型拓扑优化计算。ABAQUS 等结构有限元软件可对有限元网格单独修改，却不支持Hermitian矩阵的广义特征值求解。

本文软件基于工程与科学计算平台SiPESC 的有限元分析模块SiPESC.FEMS[17]开发。SiPESC平台为“微核心+插件”的设计模式，所有有限元分析功能被封装为名为插件的软件模块(在后文中通称软件模块)。本文依托于SiPESC.FEMS 软件模块中的模型文件导入功能、多类型单元库及后处理功能，实现了有限元方法的声子晶体能带结构分析功能，完成了声子晶体能带结构分析软件。该功能可同样用于各类周期隔振结构的仿真计算。通过将该软件与COMSOL 对比，验证了其实体单元能带结构计算能力、结构单元能带结构计算能力、大规模结构能带结构计算能力。

1 有限元能带结构分析的基本理论

声子晶体能带结构体现了弹性波在声子晶体介质中的传播能力。通过将波矢遍历不可约布里渊区的边界，计算得到对应波长的波矢在声子晶体中的传播频率，将其绘制为波矢频率关系曲线即为声子晶体的能带结构，又称色散关系曲线。

波在理想无限周期声子晶体中的传播可以看作是一种平稳状态，Bloch 证明了当简谐波在介质中传播时介质位移符合简谐波位移场u(r,t)。

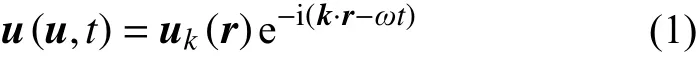
则单胞对应周期维度的维度正方向边界位移u+与维度负方向边界位移u−符合Bloch 边界条件是式(1)成立的必要条件。

因此声子晶体的能带分析问题可以归结为含Bloch 边界条件约束的广义特征值问题：

显然，用于模态分析的结构线性有限元分析中的刚度矩阵K与质量矩阵M为实对称矩阵。Bloch 边界条件中显含复系数，将原实广义特征值问题变为复数矩阵广义特征值问题。同时，由于约束的施加方法为酉合同变换，可通过Hermitian矩阵得定义公式证明约束后的矩阵Kˆ 、Mˆ为Hermitian矩阵，符合Hermitian 矩阵的定义式，即：

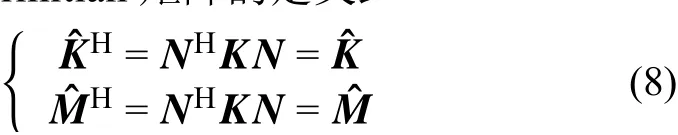
因此，声子晶体能带结构分析，经过上述公式推导，可整理为Hermitian 矩阵的广义特征值问题。能带结构分析往往只关心低阶的前几十阶特征对，而非全部特征对，需通过稀疏Hermitian 矩阵得广义特征值求解算法对其求解。

2 Hermitian 矩阵子空间迭代算法

Hermitian 矩阵是一类复共轭对称矩阵。结构有限元分析中常用的实广义特征值算法无法直接用于复Hermitian 矩阵的广义特征值问题的求解。本节在实数子空间迭代法的基础上发展了用于Hermitian 矩阵子空间迭代算法。

子空间迭代法是一类典型的特征值迭代求解方法，由BATHE[18]为求解结构动力学问题引入力学领域。子空间迭代法代表了求解大型稀疏矩阵特征值的经典思路，即通过多向量的逆迭代方法构造模态变换基底，使用正交的变换基底构建一个随着子空间迭代步数增加逐步逼近原问题特征值的特征子空间。

Hermitian 矩阵子空间迭代法的算法流程如图1所示。

图1 Hermitian 子空间迭代法算法流程Fig. 1 Hermitian subspace iterative algorithm

算法的计算细节描述如下：

1) 首先，构造数值随机、各列互相正交的实数试探矩阵。该矩阵可描述为由多列正交的试探向量组成：X0={x1,x2, ··· ,xs}。

2) 迭代求解该广义特征值问题直至问题收敛。

3) 将该试探矩阵同Hermitian 质量矩阵M相乘，得到用于逆迭代的复特征向量Un：

使用归一化后的试探矩阵重新计算式(9)～式(16)，重复迭代直至该广义特征值问题收敛，得到指定个数的特征对。

并且，由于子空间变换矩阵Qn、特征向量Rn块内正交性，一组正交向量经过正交变换所产生向量是必然正交的。因此，在Hermitian 矩阵的广义特征值求解中，同样无需做块内正交化。将Hermitian矩阵的共轭转置退化为转置，则可以推导得到用于实数子空间迭代法的归一化公式。

3 定位格节点匹配方案

在声子晶体计算中施加Bloch 边界条件是其与普通结构振动问题计算的最大区别。理想声子晶体需要对周期维度上的所有节点施加Bloch 边界条件，方法是，对空间中的主从边界节点进行一一对应的暴力搜索节点匹配。经典的三维空间暴力搜索点-点匹配算法的时间复杂度为O(n2)。当声子晶体的模型自由度增加时，节点匹配流程的计算时间占比大幅增加，匹配时间与广义特征值分析处于同一量级，大幅增加了声子晶体仿真的计算时间。因此，高效的声子晶体能带结构分析，必须降低节点匹配阶段的运算时间。本文通过引入碰撞检测领域中的定位格节点匹配方案，发展了用于声子晶体能带结构分析的主从节点匹配策略。

3.1 定位格方案描述

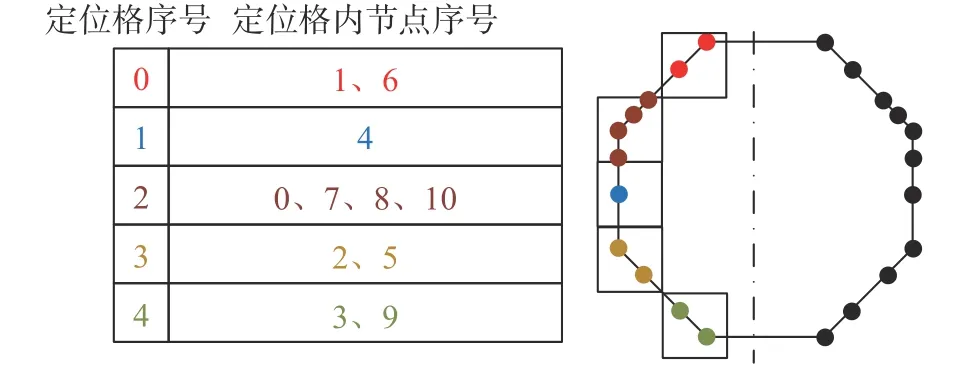
图2 定位格节点关系Fig. 2 sub-patches-node relationship

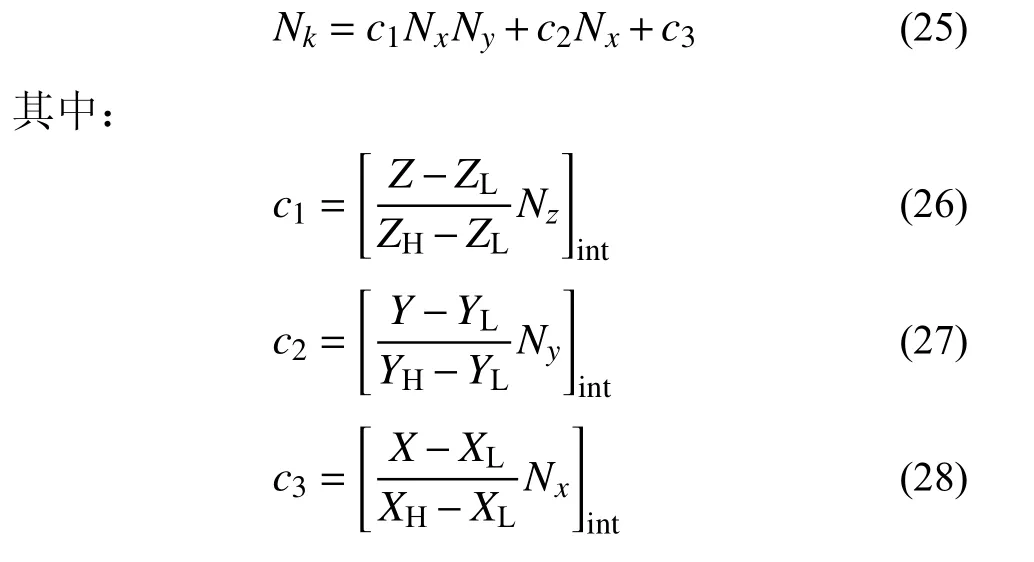
[]int为取整操作。将主节点使用节点排序后的序号整理为相应的定位格-节点关系。当计算x、y、z维度的周期边界条件时，令该周期维度的定位格数Nx、Ny、Nz等于1 即可。

3) 建立主节点和定位格的关联信息数组。该方法中需要针对主节点构造2 类数组：长度为定位格数nb的定位格数组与长度为主节点个数nm的节点数组。定位格数组记录了当前定位格第一个节点的序号，主节点数组记录了除第一个节点之外的所有节点序号。

4) 按照如下流程将定位格中的节点依次插入定位格数组和节点数组：

a) 将定位格中第一个节点序号放入定位格数组的相应位置。

b) 将该定位格中的第二个节点序号放入第一个节点序号为序号的节点数组中。

c) 对第二个节点之后的节点循环，将后一个节点序号放入以前一个节点序号为序号的节点数组中。

d) 最后将没有对应节点序号放入的定位格数组与节点数组的值设置为 −1。

图3 中展示了以2 号定位格的数据为例的节点数组与定位格数组的构建顺序。至此，主节点定位格的两类数组已经构建完成。

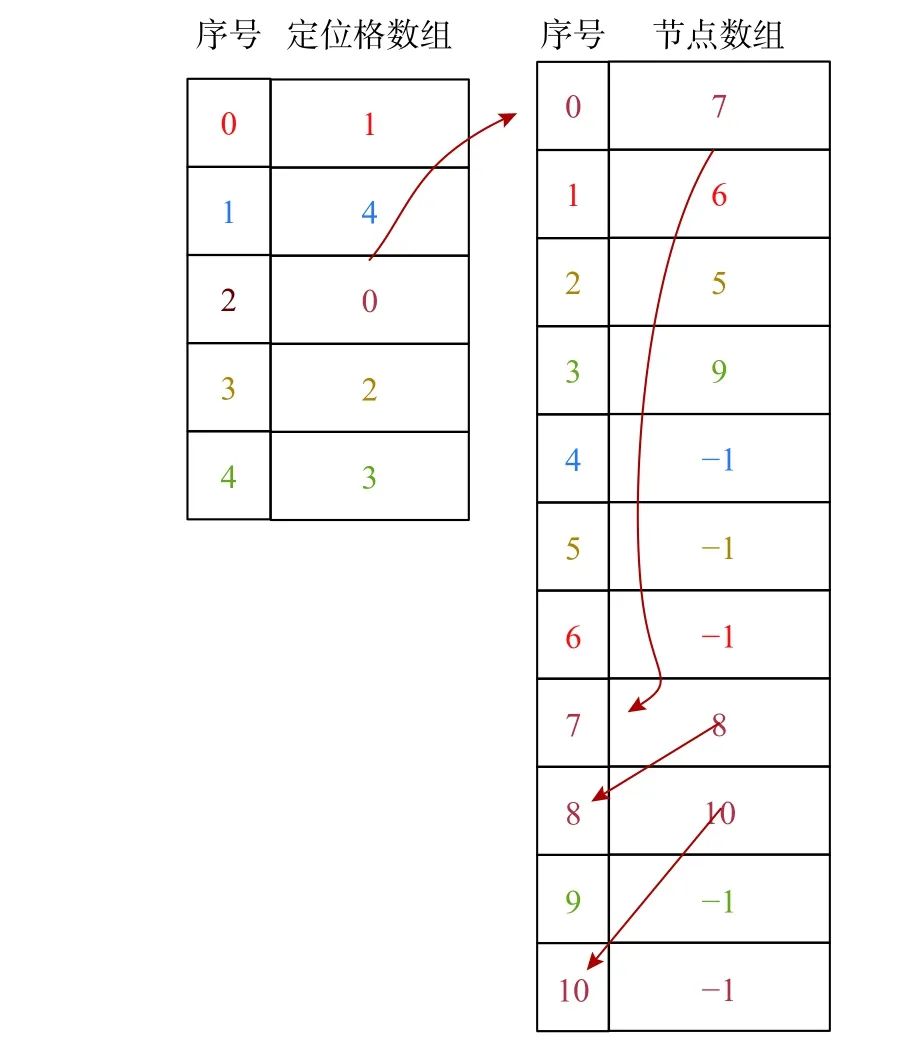
图3 主节点和定位格的关联信息数组Fig. 3 Association information array of master node and sub-patches

5) 将从节点与主节点进行匹配。先使用式(25)计算从节点与定位格的匹配关系，再顺序对节点数组和定位格数组中的节点按照插入顺序进行遍历，直至找到相应匹配节点或遍历至节点序号为−1时无匹配节点停止匹配。

3.2 节点匹配算法讨论

空间节点匹配问题是多体动力学、计算机视觉、边界元方法等问题的核心问题。其中比较典型的为：快速多极边界元问题的自适应树结构[20]，和本文引入的定位格节点匹配。这两类匹配算法的核心思想是简单且相同的，即通过增加中间层来降低节点匹配的计算量。同时，二者依托数据结构的不同造成它们搜索效率的不同。

自适应树结构根据其处理的二维/三维空间问题，分别对应四叉树/八叉树的数据格式，平均搜索速度为O(Nlog4N)/O(Nlog8N)，最劣搜索速度为O(N2)。定位格是一种哈希表数据格式，平均搜索速度为O(N) ，最劣搜索速度为O(N2)。在理想情况下，定位格方法的搜索速度更高。

对于实际的碰撞或边界元仿真等数值问题而言，节点在空间中必然分布不均。而树状数据结构可以适应空间节点分布不均的问题，定位格方法则没有该类优点。在本文所讨论的有限元网格声子晶体界面匹配问题中，在单胞界面上的网格节点(在保证良好的网格质量的前提下)在通常情况下是均布在单胞界面上的。这一现状使得本文在进行算法选择时无需考虑节点在空间中分布不均的问题，消除了定位格方法本身的劣势并可以充分发挥其优势，因此针对该问题定位格方法更为优越。同时，其占用空间大小固定，避免了反复增加数组空间的时间；数组在内存中储存连续，也使得使用C++语言中的指针遍历数组效率高于内存中不连续的列表结构。

4 声子晶体能带分析软件模块实现

本节使用前文描述的节点匹配方法及广义特征值求解算法，设计实现声子晶体的能带分析软件模块org.sipesc.fems.phononic。声子晶体的能带结构分析可归纳为3 个有别于传统有限元分析的步骤，即：

a)匹配主从节点，处理约束关系；

b)施加Bloch 边界条件；

c)在该边界条件下进行Hermitian 矩阵的广义特征值分析。

SiPESC 科学计算平台已经拥有完善的线性有限元分析功能，只需在SiPESC 平台上实现节点匹配和Hermitian 特征值求解，即可实现声子晶体的能带分析功能。

声子晶体能带分析的有限元方法具体流程如图4 所示，共可划分为11 个计算步骤。图4 虚线线框内为实现能带分析功能新增加的分析模块，其余计算步骤为SiPESC 科学计算平台已经具备的有限元分析功能，可分别使用MDofUpdate 自由度更新类与MMain 声子晶体能带结构分析主控流程类进行计算控制，其余的计算流程都可以上两计算类使用接口调用实现。二者继承自SiPESC 平台的线性流程基类MTaskManager，使用平台统一的工厂模式在有限元计算流程中调用。本节所实现的声子晶体能带分析软件模块org.sipesc.fems.phononic 整体UML 类关系如图5 如所示。

图4 SiPESC 平台能带结构分析流程Fig. 4 band structure analysis process of SiPESC platform

图5 中org.sipesc.core 软件包为SiPESC 科学计算平台的基础软件包，包含平台所需的各类基础功能、扩展所需继承的基类、代数方程组求解器与其他矩阵计算类。org.sipesc.core.engdbs 为平台的数据库软件包，负责数据库相关的IO 操作和数据库相关类型的创建与修改。org.sipesc.fems.elements 为平台的单元软件包，包含各类实体单元、结构单元、和用于自由度控制的单元控制类。

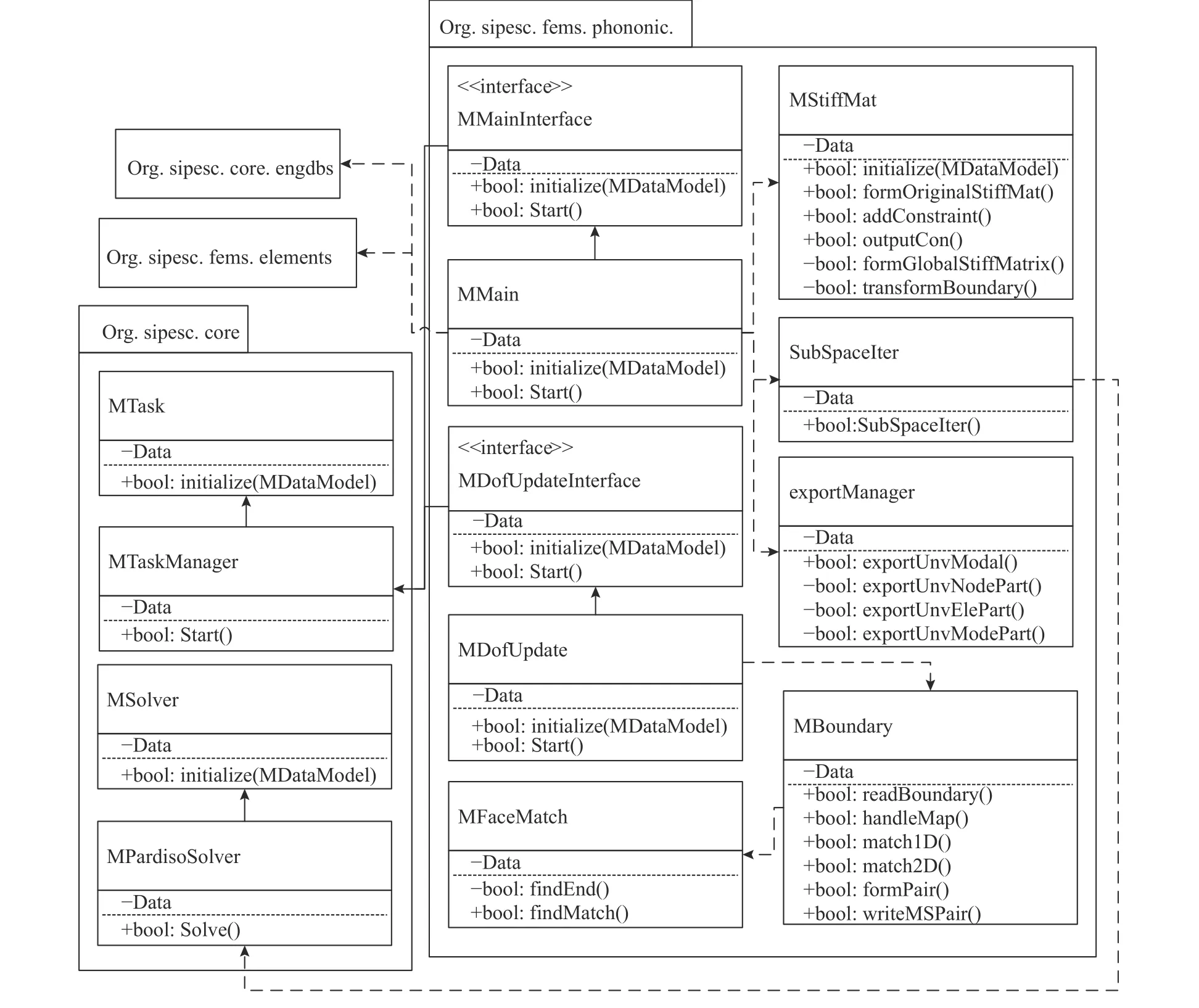
图5 SiPESC 科学计算平台声子晶体软件模块的UML 类图Fig. 5 UML class diagram of phononic crystal plugin in SiPESC platform

4.1 约束自由度处理模块

MDofUpdate 类继承于SiPESC 平台的线性计算流程类MTaskManager，拥有初始化方法initialize和计算流程方法Start。该类所实现的功能是将单胞的边界节点划分为界面主节点与界面从节点，对主从节点根据对应的周期维度进行匹配，得到一一对应的主从节点关系。最后将节点自由度划分为主从自由度，用以后续计算的自由度排序处理。

约束自由度处理的主要步骤为主从节点匹配，针对该问题抽象出边界节点匹配类MBoundary。该类通过readBoundary 方法识别主从边界节点，用以后续的算法匹配计算。声子晶体的周期性可分为1 维、2 维、3 维 这3 种，其中1 维、2 维周期边界条件都可通过3 维周期边界条件退化得到。针对具有三维周期性的声子晶体问题，可将主从边界节点类型分为3 类：点主从约束、线主从约束、面主从约束。如图6(a)、图6(b)、图6(c)所示，图中α 为顶点主自由度，a、b、c为边主自由度，A、C、E为面主自由度，其余为从自由度。图6(d)、图6(e)、图6(f)为约束关系所整理的约束关系树。首先讨论图6(a)面主从约束的处理，以最为常见的简立方体晶格为例，针对三维周期问题该晶格存在3 主面、3 从面，在不考虑顶点和棱边的情况下，主面节点与从面节点一一对应。在该主从节点匹配类中通过节点匹配方法match2D，调用MFaceMatch 类进行面节点的匹配。MFace-Match 类为定位格策略节点匹配类，该类实现了第3 节中所叙述的定位格节点匹配策略，进行快速的主从节点匹配。匹配后面主从节点可直接套用Bloch 边界条件公式进行计算。

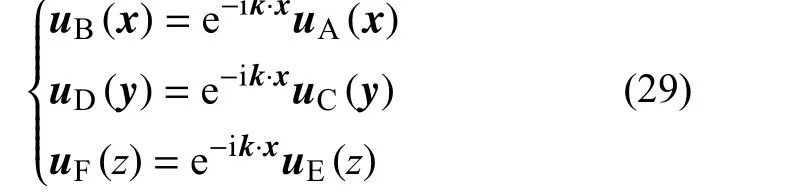
线约束与点约束会存在某一节点同时为主面节点与从面节点的情况，属于多层的主从约束匹配问题。线约束的几何关系如图6(b)，可将其整理为如图6(e)的主从约束树。简立方体晶格棱线d、g上 的节点分别在x、z周 期维度方向上是a棱线上节点的从节点，同时在x、z周期维度方向上为i棱线的主节点。经过简单的递推，可将主从关系整理为单层主从约束。而后调用match1D 方法针对边主从节点，进行匹配，边主从节点的匹配方式仅需要匹配非周期自由度的坐标即可。

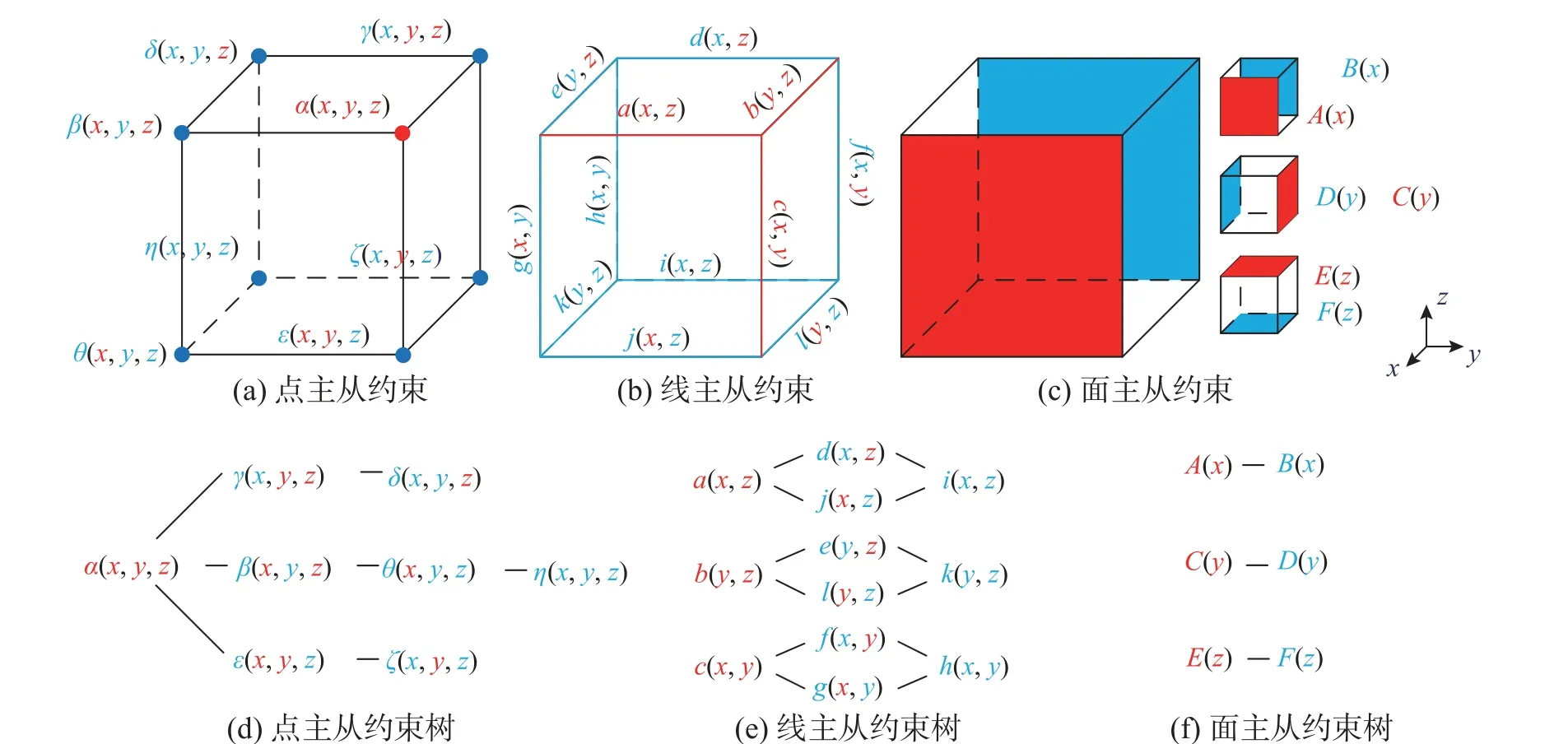
图6 三类约束几何关系及其关系树Fig. 6 Three kinds of constrained geometric relations and their relation trees

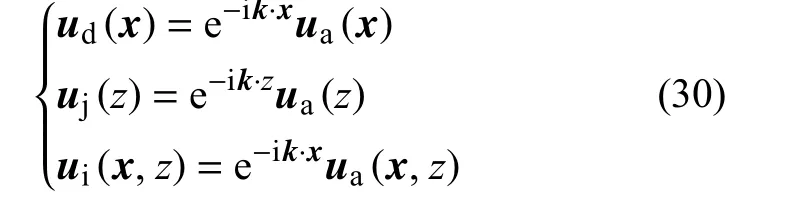
点约束同线约束在处理方法上是一致的，仅仅将2 层主从约束变为3 层主从约束，且各顶点无需进行节点匹配。

4.2 能带分析模块

MMain 流程类为声子晶体能带分析计算主控流程类，其负责了从组装无约束条件下的声子晶体单胞总刚度矩阵至计算得到能带色散曲线的全部流程具体流程如图7 所示。

图7 能带结构分析算法流程Fig. 7 Band structure analysis algorithm

有限元能带结构分析的计算主体为结构的总体刚度矩阵K，总体质量矩阵M。针对有限元总体矩阵对象，抽象出有限元总体矩阵类MStiffMat。该类通过formGlobalStiffMatrix 方法实现有限元的总体刚度矩阵组集，获得有限元的总体刚度、质量矩阵。继而通过transformBoundary 方法实现了直接消去法的约束变换矩阵N的计算。使用addConstraint 方法实现直接消去法的约束变换矩阵乘法公式(8)。最后使用outputCon 方法将施加约束变换后的总体刚度矩阵和总体质量矩阵输出至MMain流程类中。

针对Hermitian 矩阵广义特征值求解问题抽象出子空间迭代计算类SubSpaceIter。该类实现了第二节中的Hermitian 子空间迭代广义特征值算法。通过该类求解得到当前波矢约束条件下的广义特征值。

最后，针对结果输出操作抽象出结果输出对象exportorManager，该类使用exportUnvModal 方法调用私有节点数据输出方法exportUnvNodePart，私有单元数据输出方法exportUnvElePart，私有模态数据输出方法exportUnvModePart，将计算结果输出为SiPESC 平台的后处理文件类型*.unv。

4.3 能带分析算法讨论

能带结构分析可以归结为一个不断对矩阵做摄动的特征值重分析问题，这类摄动问题有一类简单的计算技巧，即使用摄动前的收敛解作为摄动后的初值。很多研究人员都已经将该技巧使用在其所做的数值研究中。这一技巧可以使特征值迭代时的试探向量较随机值更接近于终值，可以极大地加快能带计算时的收敛效率。而COMSOL中的能带计算流程(参考COMSOL 官网的声子晶体算例)是使用参数遍历方法，在不同的波矢点上反复进行初始向量随机的LANCZOS 方法，并没有继承上一步的收敛解。这是SiPESC 与COMSOL效率差异的第一点原因。

SiPESC 平台与其他商用有限元软件也有显著区别。这些结构有限元软件无法施加复数的边界约束条件，只能使用实边界条件施加约束。将刚度矩阵K划分为实部和虚部：

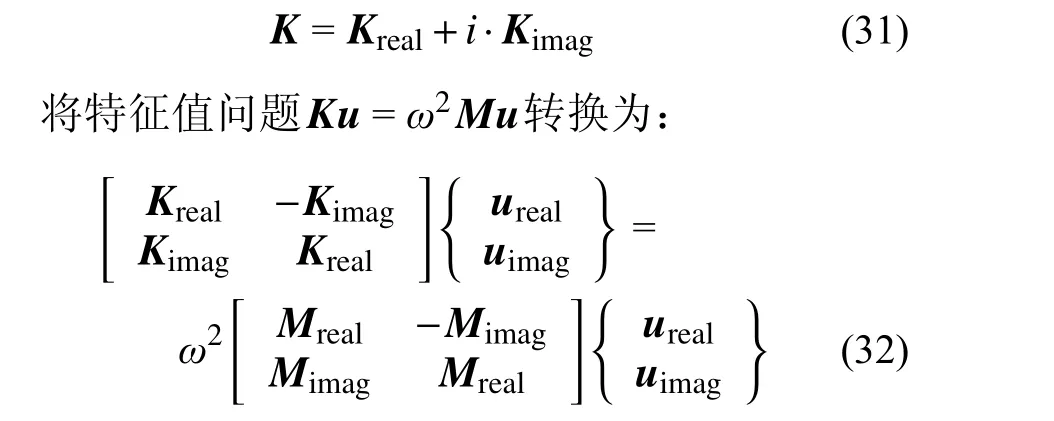
进行求解。这一算法将矩阵维度增广为2 倍，其求解的同阶特征对也会变为2 倍。例如，使用SiPESC 平台求解10 阶模态可获得10 阶特征对，使用上文所述办法只能求解5 阶特征对，每阶特征对出现2 次。由于增加求解的特征对数量时，特征值算法的计算量并非线性增长，因此二者同时计算10 阶特征值时SiPESC 计算效率远高于使用同类商业软件。

5 数值算例

5.1 计算环境说明

为验证所开发数值仿真软件模块的计算能力，在本节中分别针对实体单元组成的声子晶体模型，结构单元组成的声子晶体模型及大规模声子晶体模型进行了数值算例验证。选取文献中应用较多的多物理场数值仿真软件COMSOL Multiphysics 5.5 软件作为标准对照软件。

受现实因素限制，无法使用同一计算环境对两软件进行比较，现将它们部署的硬件环境列举于表1。显然，COMSOL 所部署的硬件环境的CPU 主频(3.20 GHz)高于SiPESC 平台所部属硬件环境的CPU 主频(2.00 GHz)，COMSOL 所部署的硬件环境的DDR4 内存全面优于SiPESC 平台的DDR3 内存。同时，通过将SiPESC 所部属的工作站并行核数限制在6 核(通过OpenMP 设置)，使两种计算环境最大并行线程数一致。因此，理论上，COMSOL 平台在算例测试上计算效率更佳。为证明本文所实现软件模块的高效性，在此忽略SiPESC 平台计算在环境上的劣势，将二者视为同环境进行对比。

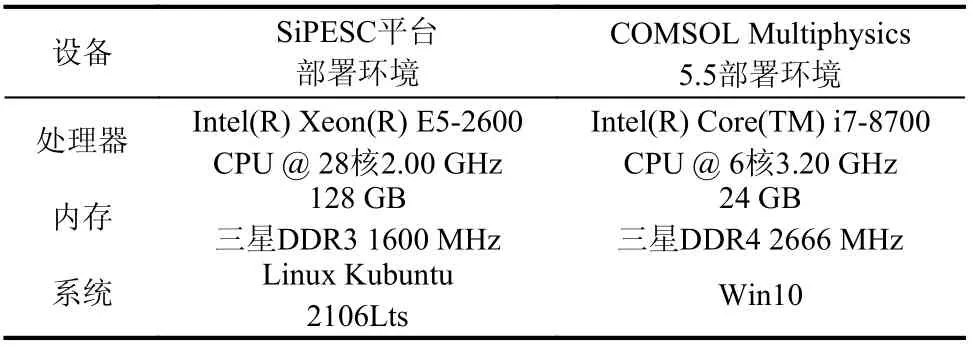
表1 材料数据Table 1 Material data

为了验证本文所实现的软件效率，选取了3 例弹性波声子晶体算例进行测试，因此在COMSOL计算中选用了固体力学模块，施加Floquet 周期性条件进行模型建立。为保证计算网格的一致性使用COMSOL 软件进行建模，MSC.Patran 前处理软件进行网格显示。在折叠结构算例中，额外使用了固体力学中壳体单元的物理场模块，以进行结构单元模拟。在第5 节中所使用的计算环境都统一遵从5.1 节的说明，不再额外在具体算例描述中叙述。

5.2 经典局域共振声子晶体算例

本节使用刘正猷于2000 年提出的经典局域共振声子晶体构型[21]作为测试模型，选取COMSOL Multiphysics 5.5 软件作为比较对象，以验证本文程序的计算速度与计算精度。该模型为3 组元声子晶体模型，使用硅橡胶包裹铅球体埋置入环氧树脂基体，结构如图8 所示。具体材料参数如表2所示，结构几何尺寸见表3。

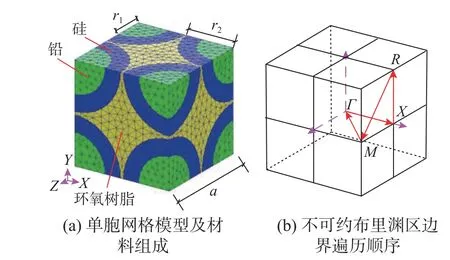
图8 局域共振声子晶体模型Fig. 8 Locally resonant sonic materials

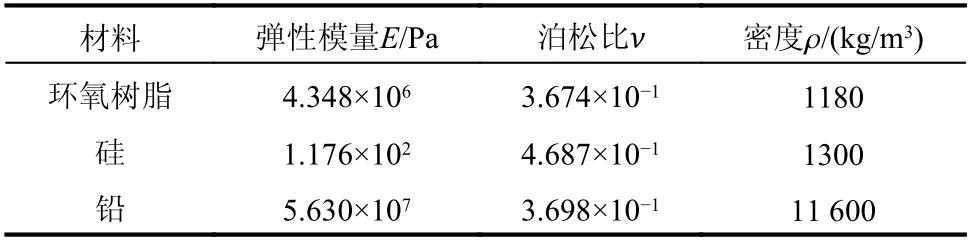
表2 材料数据Table 2 Material data

表3 几何尺寸Table 3 Geometric dimension

算例使用COMSOL 软件默认单元：10 节点二阶四面体单元，计算网格两软件完全一致。该声子晶体单胞有限元模型网格具有134 898 自由度，将不可约布里渊区边界离散为120 个波矢点。共计算20 阶模态，SiPESC 计算时间为4 h :31 min，COMSOL 计算时间为11 h : 39 min，SiPESC平台的声子晶体能带分析程序在相同的计算环境下效率显著高于COMSOL。

分析能带结构及其振动模式(图9)，显示该结构在遍历不可约布里渊区中低阶呈现出3 类共振模式。其中L1、L2、L3共振模式为铅球芯体在橡胶包覆层下围绕三个坐标轴的旋转共振模式；L7则体现为橡胶包覆层的旋转共振模式。这两类共振模式都呈现为旋转振动模式，难以与低频长行波产生耦合作用。L4、L5、L6与L′4、L′5、L6′都呈现出铅球芯体与树脂基体的反向振动，与低频长行波有较长的耦合作用，导致了较宽的第一带隙的产生。其中 Γ 点处L4、L5、L6共振模式能带穿透了L1、L2、L3共振模式能带，由于绘图工具顺序绘图的逻辑无法在图上呈现，特此注明。

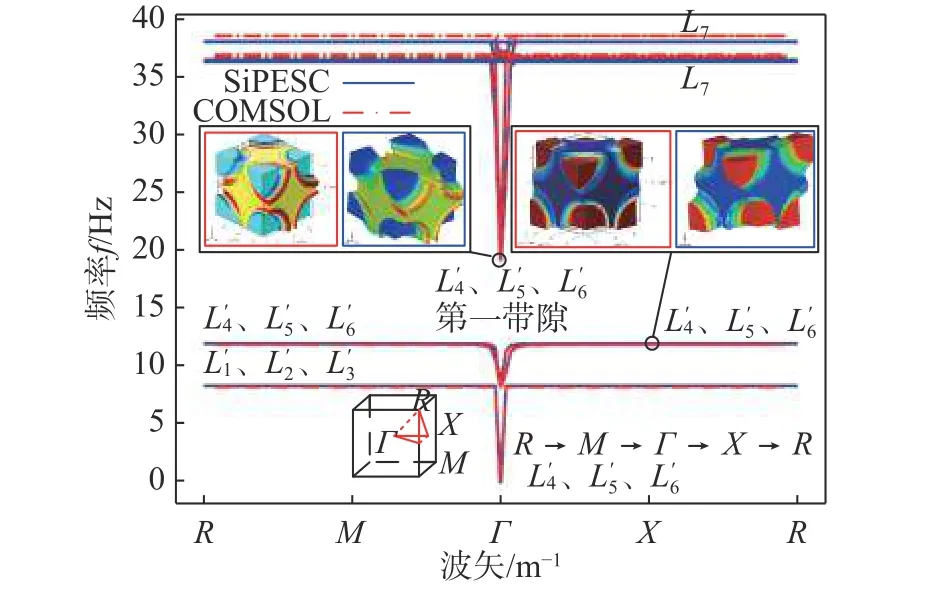
图9 局域共振声子晶体能带结构及振型Fig. 9 Band structure and mode shapes of local resonant sonic crystals

将二者能带分析结果进行对比，SiPESC 与COMSOL 能带分析结果精度在低阶一致，高阶剪切振型有较小误差。其原因大致为两类软件的单元对剪切项的处理不同。本文使用单元为防止剪切自锁现象，使用减缩积分进行积分计算。

模态振型进行对比，图9 中振型图中展示了两组振型结果。在每一组中左图为COMSOL 软件计算结果，右图中为SiPESC 软件计算结果。通过振型对比两软件计算振型一致。SiPESC 后处理显示时将二阶单元处理为线性单元显示，在计算中仍为二阶单元计算，特此注明。

该算例证明，本文所实现软件较商业软件具有一致的计算精度和较高的计算效率，基本实现了高效的声子晶体能带结构仿真功能。

5.3 大规模固/气声子晶体算例

为测试本能带结构分析软件的大规模计算性能，使用2 组元60 万自由度的气/固声子晶体模型能带结构[22]，固体材料为树脂，材料的物理性能见表4，几何结构如图10 所示，几何尺寸见表5。共计算20 阶模态。

表4 材料数据Table 4 Material data

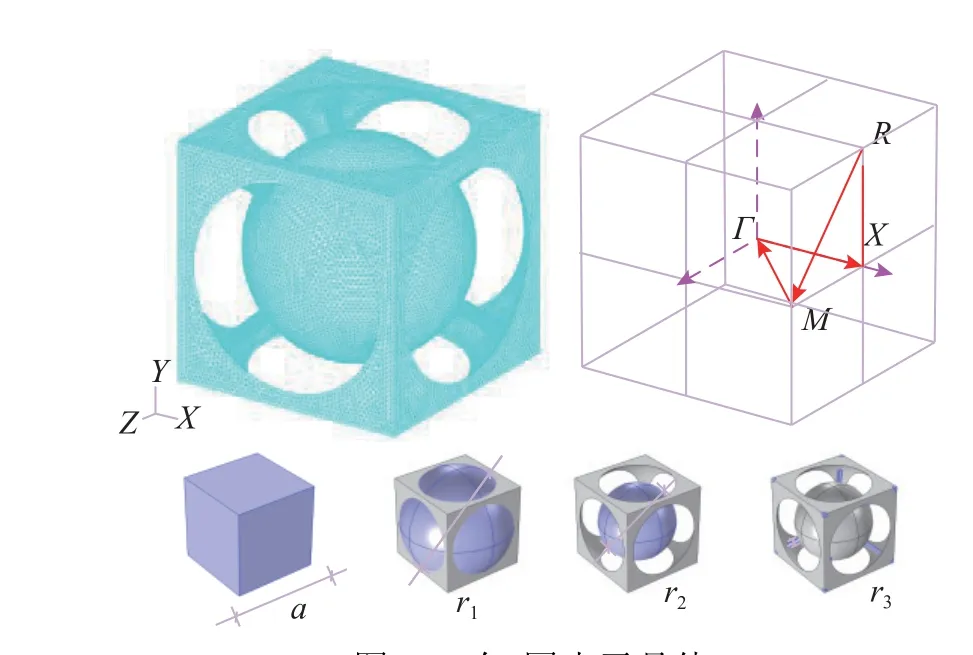
图10 气/固声子晶体Fig. 10 Gas / solid phononic crystal

表5 几何尺寸Table 5 Geometric dimension

本算例使用4 节点线性四面体单元，有限元模型具有659 952 自由度，将不可约布里渊区离散为100 个波矢点，遍历计算能带结构，计算环境同算例1。计算时间为9 小时47 分钟，能带结构如图11 所示，与参考文献[21]一致，该结构存在低频完全带隙和高频完全带隙。其中低频第一带隙与经典局域共振振型一致，芯体和框架呈现反向位移呈现局域共振特性，高频带隙带隙中心频率位于ct/2a附近，符合布拉格散射特性。图中分别呈现了第一、第二带隙两侧的单胞振型。左侧一组振型为第一带隙两侧频率的振型：内部埋置的树脂球振动和外框基体振动。右侧线框中为第二带隙两侧频率的振型：分别是横波引起的外框的扭转振动，及纵波引起的涨缩振动。

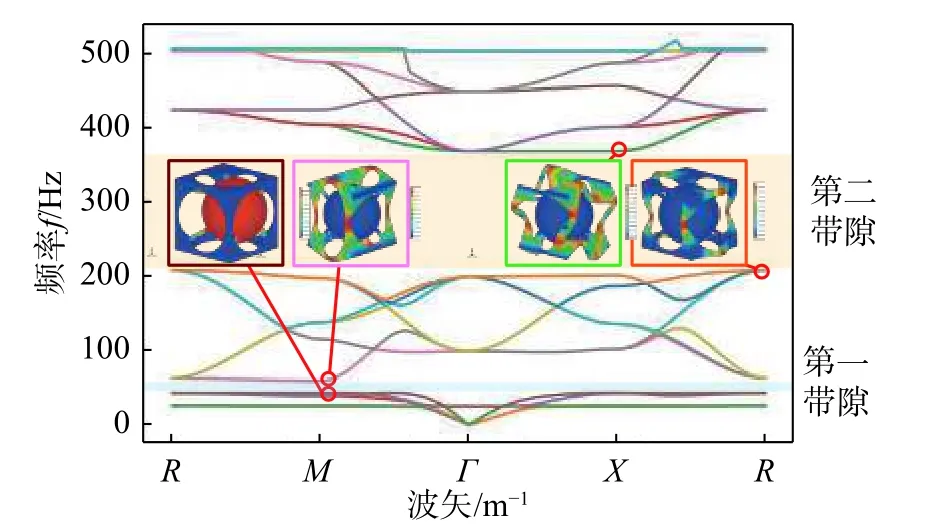
图11 气/固声子晶体能带结构及振型Fig. 11 Band structure and mode shapes of gas/solid phononic crystal

该算例证明，本文所实现软件具有大规模声子晶体能能带结构分析计算能力，适用于大规模声子晶体计算。

5.4 折叠结构声子晶体算例

为测试软件的结构单元计算能力，本节使用具有二维周期性的折叠结构声子晶体模型计算能带结构[23]。在文献调研过程中，有文章[24]指出对该模型的单胞划分会影响能带分析结果。本文基于COMSOL 5.5 版本进行了数值仿真，分别使用2 种单胞划分方式(图12 中划分方式1 和划分方式2)、2 种网格密度(1.5 k 自由度及20 k 自由度)组合进行4 类能带结构分析，使用COMSOL软件计算其10 阶能带结构，具体材料数据见表6，几何尺寸见表7。SiPESC 平台则使用划分方式1 k～1.5 k 自由度网格进行计算与COMSOL 软件进行对比。

表6 材料数据Table 6 Material data

表7 几何尺寸Table 7 Geometric dimension

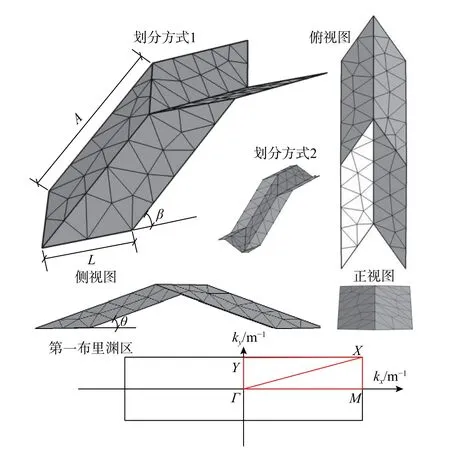
图12 折叠结构声子晶体模型Fig. 12 Folded structure phononic crystal model

对比计算得到能带结构如图13 所示，图中实线为SiPESC 计算结果，虚线为COMSOL 计算结果。SiPESC计算使用80 s，COMSOL 使用4 小时30 秒以上时间不等。从图中观察得知，5 类分析的能带结果大致相符。为探究结果的精确度，此处取子绘图13(a)与子绘图13(b)讨论。由于符合标准的有限元单元一定遵循分片实验，随着网格加密其结果将逐渐逐渐收敛至解析解。在子绘图13(a)中，划分方式1、方式2 在网格加密后都趋向于SiPESC 平台1.5 k 自由度的结果，因此可以得出结论，在针对该问题的能带结构仿真中，SiPESC 平台1.5 k 自由度时的板单元精度高与COMSOL 软件20 k 自由度时的板单元能带仿真精度。在子绘图13(b)中只有SiPESC 平台的结果中L1与L2两类共振模式的能带简并于X点。观察L1与L2两类共振模式可以得出二者是一组反对称的共振模式，在周期结构中二者的共振模式完全相同。因此L1与L2两类共振模式在X点的频率也必然是相同的，两能带必须交于一点，因此证明了SiPESC 平台结构单元能带分析精度高于COMSOL软件。

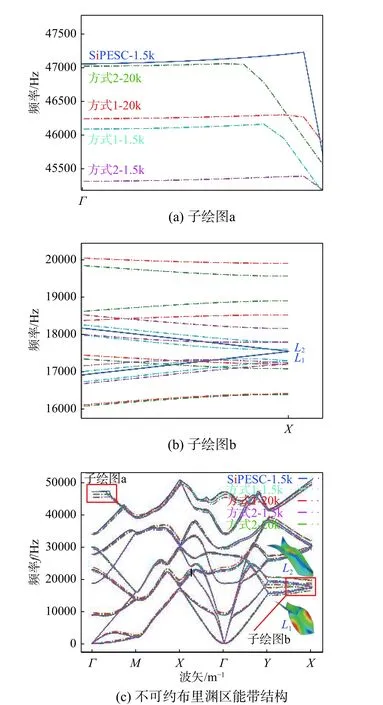
图13 折叠结构声子晶体能带结构Fig. 13 Band structure of folded phononic crystals

显然，该折叠结构不存在完全带隙，RM、RY方向能带结构相似、能带集中，符合各向异性周期结构的特性。该结构具有复杂的极化特性，已有诸多研究学者进行过讨论。

本节算例1 与算例3 与COMSOL 进行了求解效率对比，其结果为，COMSOL 软件的求解时间是SiPESC 平台计算时间的2 倍以上，验证了SiPESC 平台能带分析软件具有高效的仿真效率。求解算例1、3 时的内存负载，二者大致相当都在10 GB以下，在求解大规模模型算例2 时SiPESC 共使用内存30 GB。证明SiPESC 平台在内存充足的情况下有能力求解更大的单胞结构。精度二者大致相当，在计算结构单元时SiPESC 有明显优势。

6 结论

本文基于SiPESC 平台，实现了声子晶体高效能带结构分析软件，分别实现了用以广义特征值分析的Hermitian 矩阵的子空间迭代法，与用以进行主从节点匹配的定位格匹配方案。

(1)针对Hermitian 矩阵的广义特征值计算问题，发展了Hermitian 矩阵的子空间迭代法，并讨论了对称矩阵与Hermitian 矩阵在使用子空间迭代法时的算法差异。

(2)针对能带计算中的节点匹配问题，将用于碰撞检测的定位格匹配方案，应用于声子晶体能带结构分析的主从约束匹配。

(3)基于SiPESC 工程与科学计算平台有限元分析模块，编写了用于声子晶体能带结构仿真的软件模块。并介绍了该软件模块的架构设计和多层主从约束处理等设计细节。

(4)通过将软件模块与经典多物理场仿真软件COMSOL Multiphysics 进行对比，验证了该软件模块所实现算法具有可靠的数值精度和可观的计算效率。在此基础上计算了66 万自由度的气固声子晶体模型、100 个离散波矢点的20 阶模态自振分析，进一步验证了本文所实现软件具有高效的大规模分析能力。