套筒灌浆连接受力失效机理与有限元仿真验证
2022-11-30刘良林肖建庄
刘良林,肖建庄,丁 陶
(1. 同济大学土木工程学院,上海 200092;2. 井冈山大学建筑工程学院,江西,吉安 343009)
套筒灌浆连接能实现钢筋的可靠连接[1],可视为机械连接[2]。与其它机械连接相比,套筒灌浆连接通过套筒灌浆料硬化使被连接钢筋与套筒形成整体,形成高质量的接头结点确保结构的整体性,特别适合用于预制混凝土构件单元的连接[3−4],是预制混凝土结构中钢筋连接的主流方式[5]。目前,国内外学者开展了套筒灌浆连接受拉的广泛试验研究[3−12],传力机理研究也有报道[13],形成了有益的结论,即套筒灌浆连接应该发生套筒外钢筋断裂失效,该失效模式保障了接头性能不低于被连接钢筋的基本要求,同时实现了套筒灌浆连接组成材料充分利用及材料界面受力性能不低于被连接钢筋,提升了接头的可靠性。然而,传力机理中荷载由钢筋到达套筒的传递方式和对套筒灌浆连接受力性能的影响研究比较少见。基于此,本文从套筒灌浆连接受拉的传力机理出发,分析套筒内部的荷载传递方式与路径,探讨其对接头力学性能的影响,再基于火灾危害性与普遍性[14−16],结合已有的高温后套筒灌浆连接试验结果进行验证分析,并进一步通过有限元仿真实施拓展性研究,为形成套筒灌浆连接设计方法、促进套筒灌浆连接预制混凝土结构的安全应用提供依据与技术支持。
1 套筒灌浆连接受力机理
套筒灌浆连接由套筒、套筒灌浆料与被连接钢筋组成,并形成套筒灌浆料与钢筋、套筒与套筒灌浆料的材料界面。当套筒一端的钢筋受到拉力作用后,套筒灌浆连接的组成部分以及材料界面共同发挥作用,将荷载传递到套筒的另外一端。
1.1 材料的功能
在套筒灌浆连接的制备阶段,依靠套筒灌浆料的黏结硬化,将套筒与被连接钢筋连接成整体。投入使用后,在拉力作用下(图1),套筒灌浆连接作为整体受力,因此组成材料各自发挥抗拉作用抵抗外部荷载的影响。套筒灌浆料为高强水泥基胶凝材料(28 d 强度可达85 MPa[17]),但其抗拉能力远低于抗压强度,约为后者的十分之一[18]。套筒一般采用金属制备,也有研究表明可采用纤维增强复合材料(FRP)制备[19−21],且两种材料的抗拉能力远高于套筒灌浆料。考虑到被连接钢筋也属于金属材料,从材料受拉的角度看,套筒灌浆连接的薄弱环节主要在于套筒灌浆料。然而,事实上,通过材料间的相互作用,改变了荷载传递的路径与作用形式,充分发挥组成材料的优势性能,最后实现套筒外钢筋断裂。这种相互作用,主要依靠材料间界面的黏结达到,包括套筒与套筒灌浆料界面、套筒灌浆料与钢筋界面的黏结作用。

图1 套筒灌浆连接构造Fig. 1 Configurations of the grouted sleeve connection
1.2 套筒灌浆料与钢筋界面
当套筒灌浆连接受拉时,钢筋与套筒灌浆料之间的相互挤压作用R垂直作用在钢筋横肋表面,并可分解成纵向分量Rz、法向分量Rρ,且在横肋前形成压碎区[13],见图2(a)。为了便于分析,取靠近套筒端部的套筒灌浆料与钢筋界面的微段进行分析,见图2(b)。纵向分量Rz对套筒灌浆料形成剪切作用,由套筒灌浆料与钢筋界面的化学胶结力、摩擦力与机械咬合力形成的黏结强度抵抗,其中主要是钢筋横肋间的灌浆料键与钢筋横肋的机械咬合力。随着荷载的增大,剪应力增大,压碎区不断增长直至充满钢筋横肋间隙,界面的机械咬合力局部失效并产生初步的相对滑移,相邻的灌浆料键逐次投入工作,相对滑移逐步增大,导致已有压碎区破坏面逐渐被磨平,直至全部灌浆料键被剪断后在横肋顶部形成剪切面(图2(c)),随后荷载持续下降,相对滑移稳定增大,套筒灌浆料附着在钢筋表面随钢筋徐徐拔出套筒,界面黏结承载力由材料的摩擦力构成,发生套筒灌浆料与钢筋界面黏结滑移失效。
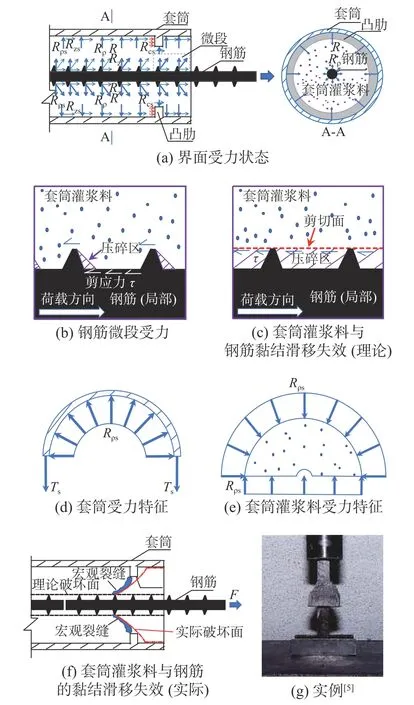
图2 套筒灌浆连接内部传力示意Fig. 2 Force transmission mode inside the grouted sleeve connection
1.3 套筒与套筒灌浆料界面
在套筒的支撑下,基于套筒灌浆料圆柱体自身力学平衡,纵向分量Rz、法向分量Rρ传递至套筒与套筒灌浆料界面,成为纵向分量Rzs、法向分量Rρs,见图2(a)所示。法向分量Rρs挤压套筒,由套筒的环向拉力平衡,见图2(d),并形成反力作用于套筒灌浆料,使得套筒灌浆料处于法向受压状态(图2(e))。纵向分量Rzs在界面形成剪应力,随着荷载的增大而增大,并由化学胶结力与摩擦力组成的界面黏结强度平衡。由于化学胶结力较小,套筒灌浆料与套筒的界面黏结强度主要为二者的摩擦力。当剪应力克服黏结强度,界面出现滑移导致黏结承载力由静摩擦力转化为动摩擦力,荷载下降,界面相对滑移增大。由于套筒灌浆料抗拉强度较低,套筒中部的套筒灌浆料圆柱体(图1(b)中钢筋的对接空隙)容易纵向受拉拉断,断裂的套筒灌浆料圆柱体与钢筋整体被拔出套筒(如CS-06 试件[13]),发生套筒灌浆料与套筒界面的黏结滑移失效。
1.4 失效模式
基于上述分析,套筒灌浆连接受拉后,发生的失效模式包括三种情形,即材料的断裂、套筒与套筒灌浆料界面黏结滑移失效、钢筋与套筒灌浆料界面黏结滑移失效。对于材料的断裂,还需要进一步明确断裂材料的类型:首先是套筒灌浆料,根据肖建庄等[22]的计算,其断裂不能决定套筒灌浆连接的力学性能;其次是套筒,根据国内外的研究[7−9],试件达到峰值荷载后,套筒仍然处于弹性状态,平均应力不到屈服强度标准值的0.5 倍[18],表明套筒不应该发生断裂;最后是钢筋,根据作者实测[23],钢筋应力从靠近加载端开始,沿着钢筋黏结长度的增大而减小,因此钢筋断裂有可能发生,但是发生的位置应该位于套筒外。
当在套筒内表面设置凸肋后(图1(b)),平衡套筒灌浆料与套筒相对滑移引发的挤压作用Rcs(图2(a)),并阻碍二者的相对滑移,抑制发生套筒灌浆料与套筒界面黏结滑移失效。实际工程中,为了安装密封胶塞,凸肋往往离套筒端部有一定距离(图2(f)):套筒灌浆料连接受拉后,由于凸肋的有利作用,套筒凸肋之间的部位只发生套筒灌浆料与钢筋界面的黏结滑移失效,即理论破坏面位于钢筋横肋顶部;同时,凸肋的楔入作用,首次改变了破坏面的位置;由于同等条件下,套筒与套筒灌浆料界面的黏结承载力低于钢筋与套筒灌浆料界面的值[13,22],在凸肋与套筒端部的范围,应该发生套筒灌浆料与套筒界面黏结滑移失效,再次改变破坏面的位置。因此最终发生复合式的界面黏结滑移失效,见图2(f),这可用EINEA 等[5]试验研究的Type 3 试件来证明(图2(g))。相对套筒长度,密封胶塞长度较短,因此总体上,该复合式失效模式仍然属于套筒灌浆料与钢筋界面黏结滑移失效。
总之,一般情况下,当套筒内表面无凸肋时,套筒灌浆连接受拉后可能发生的失效模式包括套筒外钢筋断裂、套筒灌浆料与钢筋界面黏结滑移失效、套筒与套筒灌浆料界面黏结滑移失效等三种类型之一。当套筒表面具有凸肋或具有类似功能的构造(如锥形套筒[7])与构造物(如焊接钢环[5,9])时,套筒灌浆连接受拉后可能发生的失效模式则为套筒外钢筋断裂、套筒灌浆料与钢筋界面黏结滑移失效中的失效类型之一。
2 套筒灌浆连接受拉承载力计算方法
根据上述受力特征、失效模式,套筒灌浆连接受拉承载力的计算方法确定如下。
2.1 套筒与套筒灌浆料界面黏结承载力
假设界面黏结强度沿着套筒长度均匀分布,忽略化学胶结力,只考虑摩擦力,建立界面的黏结承载力F1计算表达式,见式(1)。其中,µ为界面摩擦系数,Dis为套筒内径,lb为钢筋黏结长度。应该指出的是,界面的摩擦系数µ,偏安全考虑,建议取动摩擦系数值。根据图2(d)的套筒受力平衡,建立法向分量Rρs的计算方法见式(2),其中Ts为纵向单位长度套筒的环向拉力。由于套筒处于弹性状态,Ts的计算方法见式(3),其中tw为套筒厚度、fys为套筒屈服强度。结合表达式(1)~式(3),可得套筒灌浆料与套筒界面黏结承载力。

2.2 套筒灌浆料与钢筋界面黏结承载力
基于常温下作者的实测结果[23],并结合高温后拔出试验试件的数据,通过拟合分析建立无侧压的情况下高温后套筒灌浆料与钢筋界面的黏结强度τu计算方法见式(4)。根据图2(e),灌浆料处于法向受压状态,有助于提升套筒灌浆料与钢筋界面的黏结强度,国内外文献[5, 8 − 9]普遍采用法向应力的平方根形式考虑该作用,即得到界面黏结强度的修正值τu,0,具体的计算方法见表达式(5)。假设套筒灌浆料与钢筋界面的黏结强度为均匀分布,界面的黏结承载力F2计算方法见表达式(6)。式(6)中的整体系数k2主要用于反映套筒的影响,研究表明套筒的引入能够增大钢筋的刚度[24],提升套筒灌浆连接接头整体性。
式中:d为钢筋直径;k为拟合系数,表征荷载类型的影响程度;fcg为套筒灌浆料抗压强度;k1为考虑法向应力Rρs、钢筋黏结长度lb、钢筋直径d等因素共同影响的组合系数;k2为套筒灌浆连接的整体系数,表征套筒对钢筋刚度的增强作用。
2.3 钢筋受拉承载力
规程[17]要求套筒灌浆连接发生套筒外钢筋断裂失效,表明接头受力过程中,钢筋能达到其抗拉强度,因此建议套筒灌浆连接中钢筋受拉承载力F3计算方法如表达式(7)所示。
式中:fstk为钢筋抗拉强度标准值;As为钢筋横截面面积,其余参数含义同前。
2.4 套筒灌浆连接受拉承载力与失效模式识别
基于上述传力机理的分析,总结套筒灌浆受拉承载力F的计算方法,即取表达式(1)、式(6)、式(7)计算结果的最小值,见式(8)。根据承载力取值结果,获得套筒灌浆连接受拉的失效模式:当F=F1,表明套筒灌浆料与钢筋界面黏结承载力、钢筋受拉承载力均不低于套筒灌浆料与套筒界面黏结承载力,即发生套筒灌浆料与套筒界面黏结滑移失效,必须要指出的是,一般的商用套筒内表面均含有凸肋,因此该失效模式普遍不会发生;当F=F2,表明套筒灌浆料与套筒界面黏结承载力、钢筋受拉承载力均不低于套筒灌浆料与钢筋界面黏结承载力,即发生套筒灌浆料与钢筋界面黏结滑移失效;当F=F3,表明套筒灌浆料与套筒界面、套筒灌浆料与钢筋界面的黏结承载力均不低于钢筋受拉承载力,即发生套筒外钢筋断裂失效。
3 套筒灌浆连接承载力计算方法应用
3.1 材料性能修正
火灾是建筑服役期间可能遭遇的重大灾害之一。高温作用后,材料的性能下降。本课题组、马江剑[25]根据试验数据,通过拟合分析建立高温后套筒灌浆料抗压强度计算方法,分别见式(9)、式(10)。高温后HRB400 级钢筋的屈服强度、抗拉强度以及弹性模量按照余志武等[26]提出的方法计算。实测结果表明[27−29],高温后套筒灌浆连接的套筒始终处于弹性状态,其屈服强度的计算方法也参照余志武等[26]提出的高温后钢筋屈服强度计算方法执行。

3.2 拟合系数k 的确定
根据国内外套筒灌浆连接单调递增受拉作用的试验[5,7, 30 −31],收集到27 组发生套筒灌浆料与钢筋界面黏结滑移失效的试件,假设表达式(5)、式(6)中系数k1=k2,将黏结承载力实测值F2,tt与按照式(6)获得的计算值F2,tc绘制于图3(a)中,发现k=0.203 时,二者存在较好的线性关系,相关系数可达0.96。同时,利用国内外反复拉压加载试验结果[4,32 −33],收集19 组发生套筒灌浆料与钢筋界面黏结滑移失效的试件数据,仍假设表达式(5)、式(6)中系数k1=k2,将黏结承载力实测值F2,ct与计算值F2,cc(按照式(6))绘制于图3(b)中,发现k=0.158 时,二者也存在较好的线性关系,相关系数可达0.97。因此,单调递增受拉、反复拉压作用时,建议表达式(5)中拟合系数k分别取0.203、0.158,表明反复拉压作用对套筒灌浆连接受力性能具有重大影响,造成套筒灌浆料与钢筋界面黏结承载力相对单调递增受拉的值下降幅度可达22.0%。

图3 不同荷载作用下界面黏结承载力拟合Fig. 3 The fitting coefficient of connection under different loadings
3.3 组合系数k1 与整体系数k2 的确定
遭遇火灾后经过加固的结构还可能遭遇地震作用并发生失效,基于此,本课题组通过试验研究了高温后(最高温度600 ℃)套筒灌浆连接反复拉压的力学性能。研究结果表明[27−29],试件(商业套筒,内有凸肋)的失效模式主要包括两种类型:套筒外钢筋断裂(失效模式Ⅰ)、套筒灌浆料与钢筋界面黏结滑移失效(失效模式Ⅱ),表明前述关于套筒灌浆连接失效模式种类的分类结果正确可行。表1 中列出了钢筋为HRB400 级、灌浆料A 与C 系列共72 个、24 组试件的峰值荷载平均值Ft以及实测失效模式。当假设k2等于1 时,按照式(7)计算钢筋抗拉承载力F3c,见表1 所列。很明显地,试件实测值Ft高于计算值F3c,即套筒的引入提升了钢筋的整体性,视为套筒灌浆连接的整体系数k2,并将其值也列于表1。发生失效模式Ⅱ的试件整体性已经下降,出于安全考虑将整体系数值取为最大值,因此表1 中采用“≤”符号表示。根据电镜扫描技术[34],高温作用后套筒灌浆料内部出现裂缝与孔隙导致套筒灌浆料与钢筋黏结强度下降,400 ℃高温作用后试件失效模式发生转变,600 ℃高温作用后黏结强度低于钢筋屈服强度。因此,对于>400 ℃高温作用后的套筒灌浆连接整体性系数建议取1.0。
根据表1 中整体系数的取值情况,发现当k2=1.18 时,钢筋抗拉承载力的修正值F3′c与实测值Ft非常接近,最大偏差不超过8.0%,表明整体系数取1.18 较为合理,该值也与ACI 318−14[35]中要求的系数1.25 较为接近。为了便于分析,建议整体系数k2取1.2,由此得到组合系数k1也取1.2,该值与我国长期以来的恒载分项系数一致,有助于实际应用与推广。
3.4 修正后套筒灌浆连接承载力计算方法初步应用
根据上述系数取值情况,利用表达式(6)计算高温后套筒灌浆连接反复拉压荷载作用下的界面黏结承载力F2c,a、F2c,b,对应分别利用表达式(9)、式(10)计算高温后套筒灌浆料抗压强度,均列于表1。从表1 发现:≤400 ℃高温作用后,F2c,a、F2c,b近乎相等(最大偏差5.6%)且均高于F3′c(幅度可达28.2%以上),表明界面黏结承载力高于钢筋抗拉承载力,应该发生套筒外钢筋断裂,即失效模式Ⅰ,将其作为预测结果列于表1;600 ℃高温作用后,F2c,a、F2c,b相差明显且前者高于后者,幅度可达15.6%,同时前者、后者分别大于(幅度最高为4.4%)、小于(幅度最高为12.5%)F3′c,表明F2c,a的计算结果更精确。综合不同高温作用后的套筒灌浆连接反复拉压作用下承载力计算情况,建议采用表达式(9)计算高温后套筒灌浆料残余抗压强度,并基于由表达式(6)计算的黏结承载力(表1 中F2c)高于由表达式(7)计算的抗拉承载力(表1 中F3′c)28.2%而建议该差值大于28%时,判断试件发生失效模式Ⅰ,否则发生失效模式Ⅱ,预测情况列于表1。可以发现,除试件组GS-A-400-CH 外,其余试件组失效模式的预测情况与实测结果完全一致,表明表达式(6)、式(9)用于高温后套筒灌浆连接反复拉压力学性能分析是可行的。

表1 套筒灌浆连接承载力计算方法的应用Table 1 Applications of the new method for bearing capacity of connections
4 套筒灌浆连接受力有限元仿真分析
研究发现[27−29],高温后套筒灌浆连接反复拉压作用下失效模式在400 ℃、600 ℃时完全不同,同时≤600 ℃高温作用后试件承载力下降幅度不超过10%。因此,有必要进一步明确套筒灌浆连接失效模式转变以及承载力明显下降的临界温度,有助于识别高温后套筒灌浆连接的适用性与安全性,为此利用ABAQUS 软件开展有限元仿真分析。
4.1 模型建立
根据规程[36]的规定,套筒灌浆连接的反复拉压作用相当于地震作用,因此套筒灌浆料受压本构采用本课题组建立的动态荷载作用下单轴受压本构模型(表达式(11)),见图4(a)的第一象限中曲线[37],钢筋本构采用双折线模型(图4(b)),套筒采用理想弹塑性模型(图4(c)),均采用软件中C3D8R 单元模拟。套筒灌浆料与套筒界面采用Tie连接,套筒灌浆料与钢筋界面采用Cohesive 单元连接。在牵引力作用下,Cohesive 单元最常用的本构模型为双折线[38−39],见图4(d),在软件中采用COH3D8 单元模拟。在图4(d)中,根据图2(e)套筒灌浆料受力特征,σmax取套筒灌浆料抗压强度;τmax采用表达式(5)确定;s0、sf取值根据文献[23]建立的方法确定,分别为0.77 mm、13.55 mm。根据对称性,建立基于XOY 面的半结构模型(图5(a)),单元数为7232,网格最大尺寸为12.5 mm,网格划分情况见图5(b)。
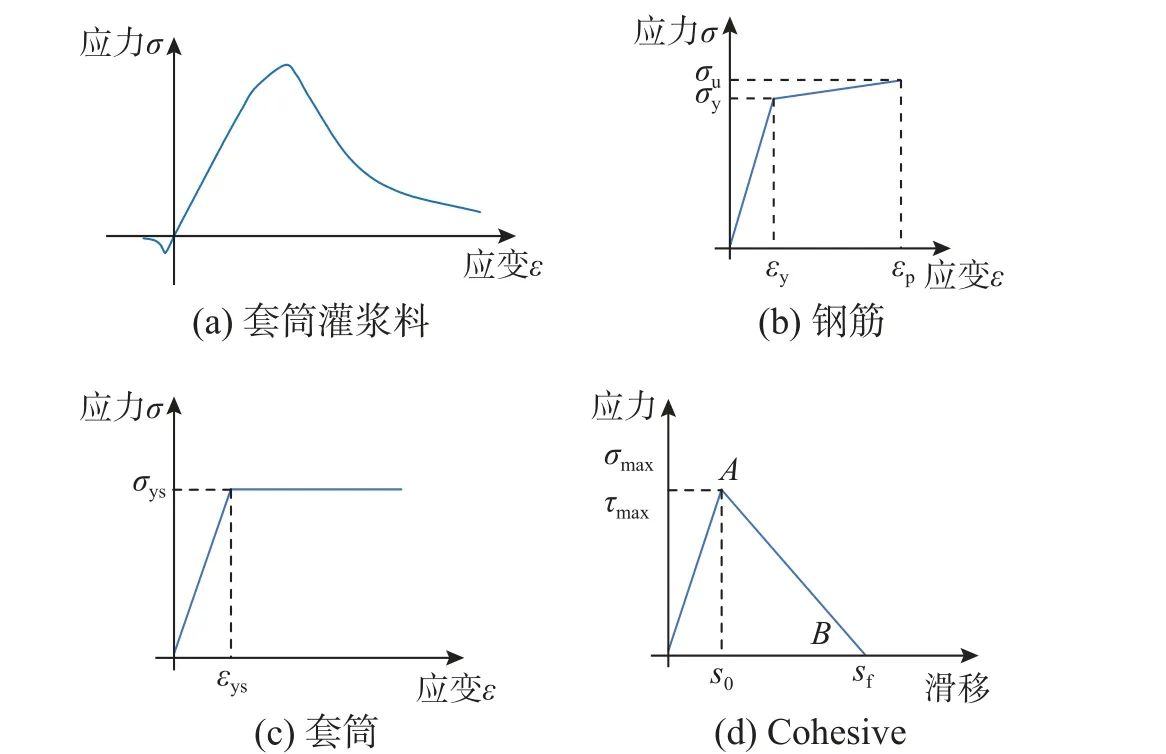
图4 材料本构Fig. 4 Constitutive models of materials

图5 模拟对象Fig. 5 The simulation model

4.2 结果对比与验证
由于≤400 ℃高温作用后试件的力学性能接近,因此以400 ℃为代表并联合600 ℃,开展文献[27 − 29]中C 系列高温后套筒灌浆连接反复拉压作用仿真分析,得到套筒灌浆料与钢筋界面损伤变量值(D)与加载时程(tc)的关系、荷载-位移曲线、加载完成状态分别见图6、图7、图8 所示。在图6 中,设置0.7 为损伤临界值,即超过该值后发生严重破坏或失效、小于该值则基本完好[40]。从图6发现400 ℃高温作用后模拟对象在UT、CH、CL分别作用下的套筒灌浆料与钢筋界面损伤变量值分别为0.39、0.36、0.34,均小于0.7,表明界面基本完好;600 ℃高温作用后模拟对象在三种加载方式下的损伤变量值均达到1,表明界面失效。在图7 中,列举了试件实测与模拟对象的荷载(F)-位移(Δ)曲线,发现:模拟与实测结果的曲线特征基本一致,且模拟曲线的上升段与强化段和钢筋本构关系曲线形状一致(图4(b));模拟结果曲线的上升段与实测结果几乎完全重合;400 ℃高温作用后,模拟对象的下降段与实测结果一致,也呈现竖直线性下落的特征;600 ℃高温作用后,模拟对象的下降段与实测结果一致,均呈现非线性下落的特征;峰值荷载与表1 中的实测值非常接近,最大偏差约为6.0%。从图8 中发现,400 ℃高温作用后,模拟对象均出现套筒外钢筋断裂失效(失效模式Ⅰ),与实测结果完全一致(表1);600 ℃高温作用后,模拟对象中套筒中部的矩形框(指套筒中部因为凸肋隔断形成的套筒灌浆料圆柱体空隙),相对初始状态(图6(d))明显增大,即套筒灌浆料与钢筋发生明显相对位移,结合图6中该界面的损伤情况,判断模拟对象发生套筒灌浆料与钢筋界面黏结滑移失效(失效模式Ⅱ),与表1 中的实测一致。因此,高温后套筒灌浆连接反复拉压作用有限元仿真分析方法正确可行。
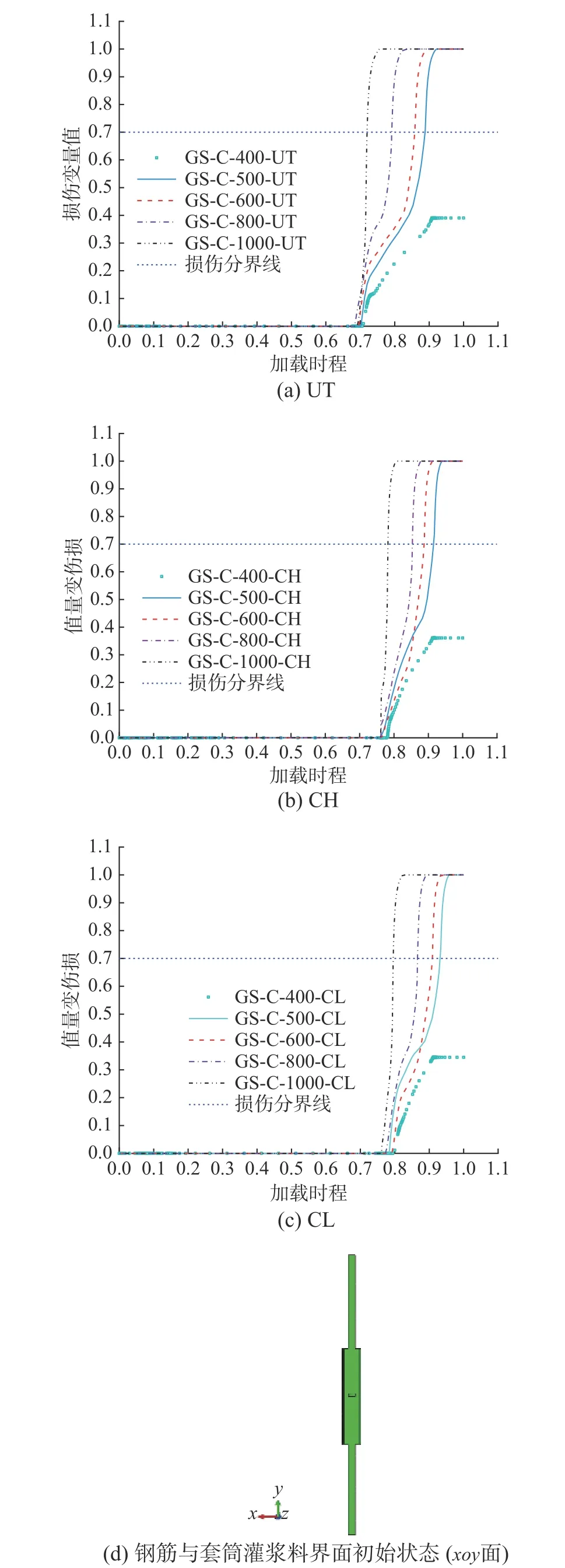
图6 高温作用后试件的套筒灌浆料与钢筋界面损伤变量发展特征Fig. 6 Damage developments between grout and steel rebar of heat-damaged grouted sleeve connections
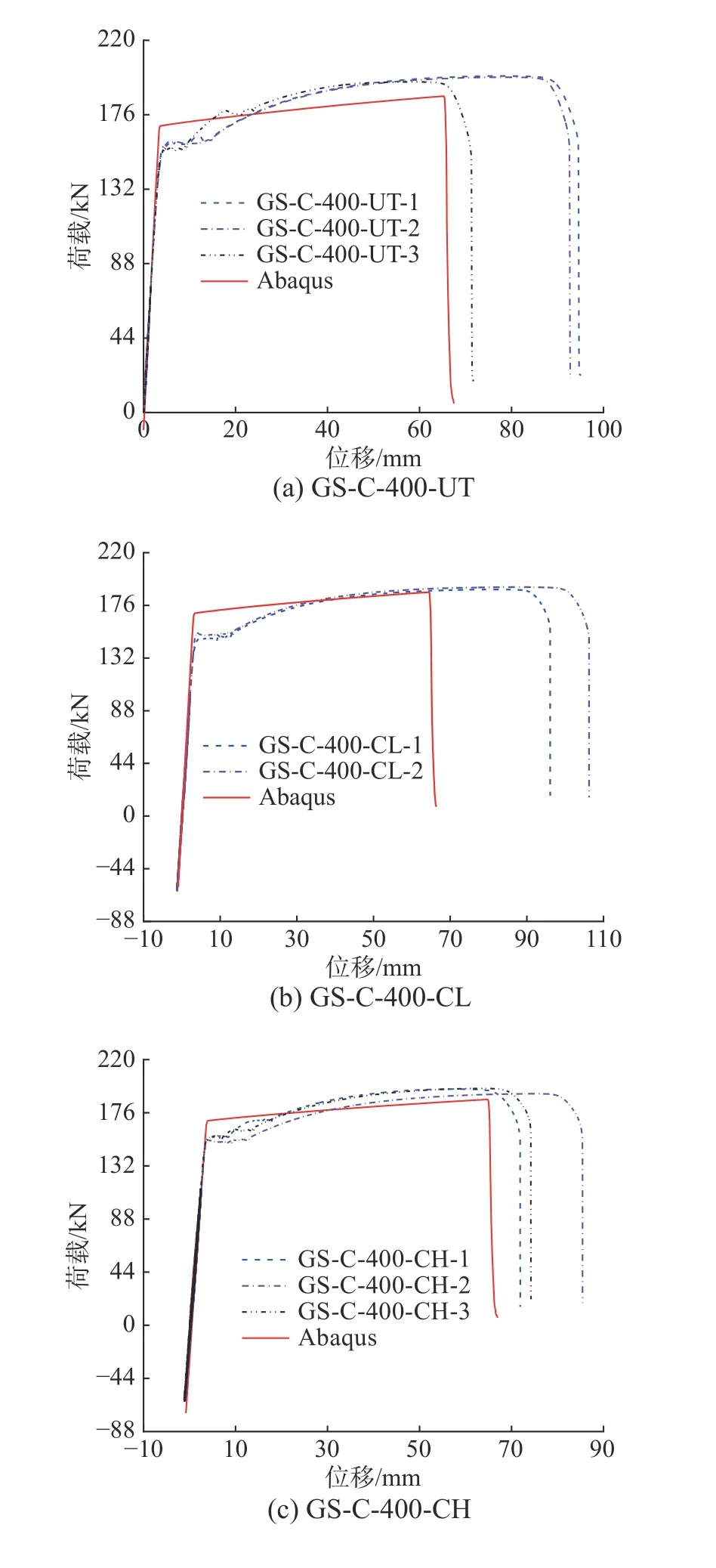
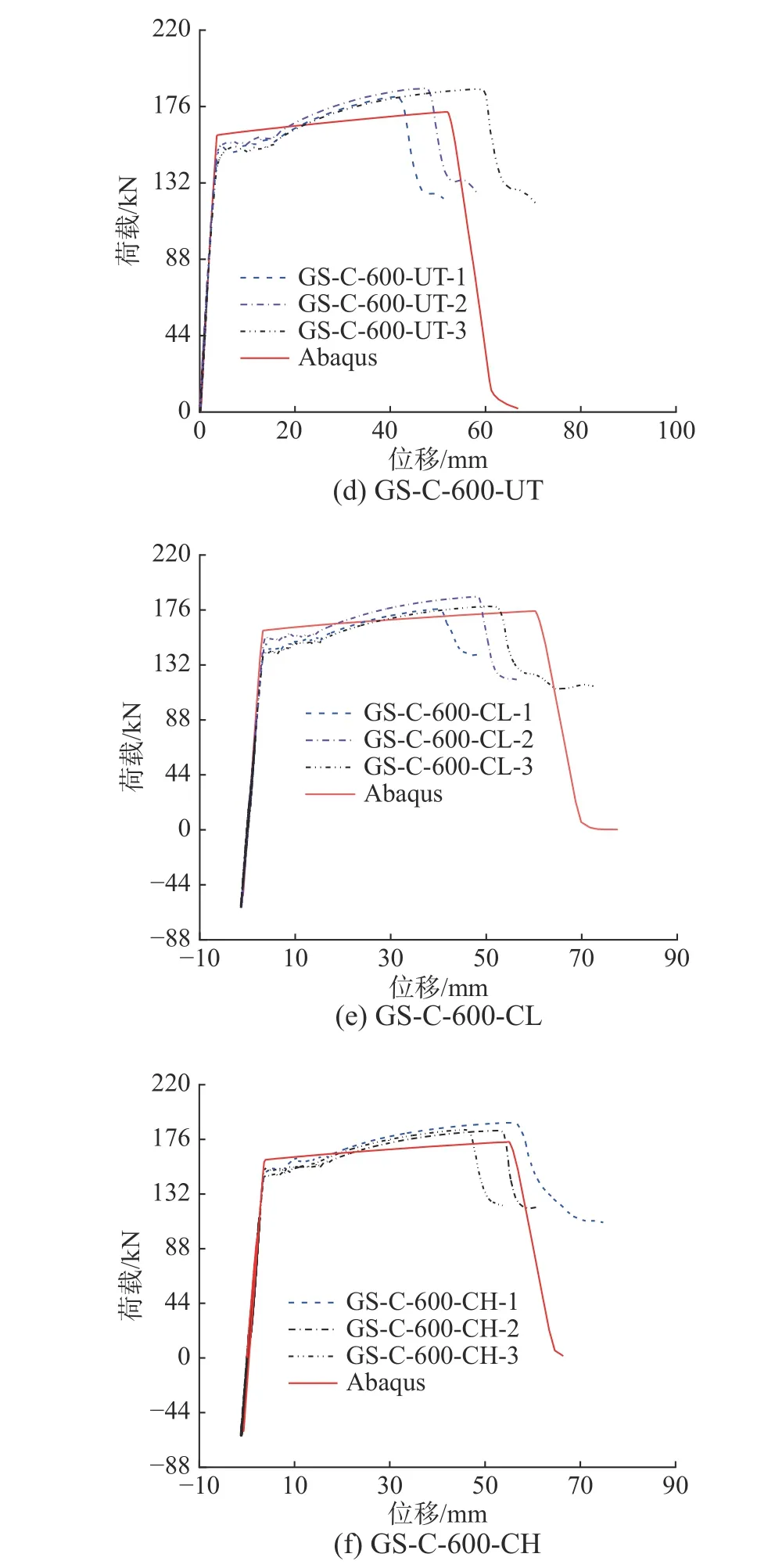
图7 荷载(F)-位移(Δ)曲线Fig. 7 Curves of loads and displacements


图8 失效模式示意Fig. 8 Failure modes from simulations
4.3 变参数分析
基于上述模拟方法的可行性,增加500 ℃、800 ℃、1000 ℃等三种目标温度,进一步开展高温后套筒灌浆连接反复拉压性能的仿真分析。将套筒灌浆料与钢筋界面的损伤变量值发展时程绘制于图6,并列出模拟对象的荷载-位移曲线、加载完成后的失效特征分别见图9、图10 所示。同时,还将模拟对象的峰值荷载列于表2。从图6 发现,500 ℃、800 ℃、1000 ℃高温作用后界面损伤变量值均达到1,表明界面完整性遭到破坏;在图9 中,发现中部矩形框相对初始状态明显增大,而且温度越高,矩形框越大,且钢筋并未断裂。因此,判断500 ℃、800 ℃、1000 ℃高温作用后模拟对象发生失效模式Ⅱ,即400 ℃为套筒灌浆连接失效模式转变的临界温度。从图10 还发现,500 ℃、800 ℃、1000 ℃高温作用后模拟对象荷载-位移曲线的上升段与强化段和钢筋本构关系曲线形状一致(图4(b)),但下降段比常温下模拟对象曲线下降更平缓,温度越高越缓和且强化段越短。


图9 高温后(500 ℃、800 ℃与1000 ℃)模拟对象失效特征Fig. 9 Failure modes of heat-damaged connections after exposed to 500 ℃, 800 ℃ and 1000 ℃
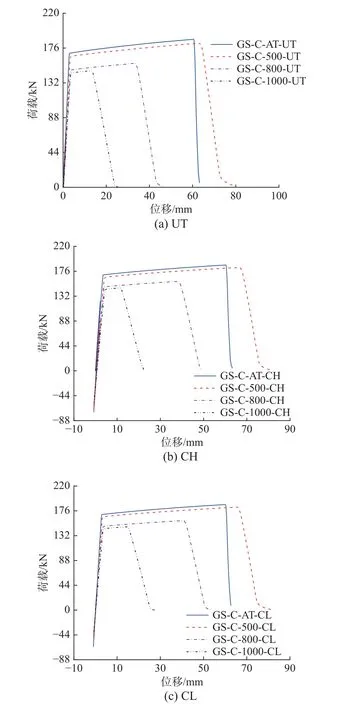
图10 高温后(500 ℃、800 ℃与1000 ℃)套筒灌浆连接模拟对象的荷载-位移曲线Fig. 10 Curves of loads and displacements of connections after exposed to 500 ℃, 800 ℃ and 1000 ℃
将三种高温作用后的峰值荷载列于表2。从表2 发现,相对常温下的峰值荷载模拟值187.0 kN,500 ℃、800 ℃、1000 ℃高温作用后模拟对象的峰值荷载下降幅度最小分别为2.3%、15.1%、20.6%,即≥800 ℃高温作用后峰值荷载下降幅度明显,可达15%以上。同时,基于500 ℃、800 ℃、1000 ℃高温作用后模拟对象在反复拉压作用下均发生失效模式Ⅱ,因此以表达式(6)计算套筒灌浆料与钢筋界面的黏结承载力,也列于表2。对比模拟值、计算值发现,二者最大偏差8.2%,比较接近。此外,根据表1、2 发现,500 ℃、800 ℃、1000 ℃高温作用后套筒灌浆连接的峰值荷载计算值相对常温值(200.1 kN)下降幅度最小分别为0.9%、13.4%、22.0%,与模拟结果的下降幅度非常接近,再次表明表达式(6)的计算结果准确可行。根据模拟情况与计算结果,发现≥800 ℃高温作用后套筒灌浆连接峰值荷载相对常温值出现明显下降,因此,建议400 ℃、800 ℃分别为套筒灌浆连接反复拉压作用下失效模式转变、峰值荷载明显下降的临界温度。除以上分析结果外,以下的已有研究成果也可作为该建议的佐证:

表2 高温后套筒灌浆连接承载力计算与模拟Table 2 The bearing capacity of connections by calculations and simulations
1)关于400 ℃为失效模式转变临界温度的参考。根据肖建庄等[41− 42]的研究成果,≤400 ℃高温作用下高强水泥基胶凝材料的强度下降缓慢,>400 ℃高温作用下高强水泥基胶凝材料的强度急剧下降;马江剑[25]的电镜扫描结果显示,400 ℃高温作用后水泥基胶凝材料发生结晶水脱离,500 ℃高温作用后水泥基胶凝材料中的Ca(OH)2分解为CaO 与H2O,胶凝材料的性能发生改变,即变得疏松、裂纹变大;套筒灌浆料出现裂缝与缝隙,则导致胶结力下降,出现失效模式的转变[34]。
2)关于800 ℃为承载力明显下降临界温度的参考。以屈服强度为例,相对常温值,700 ℃、800 ℃、900 ℃高温作用后钢筋屈服强度下降幅度分别为9.3%、12.3%、14.3%[26],可以看出800 ℃为钢筋的抗拉承载力设计值明显下降的临界温度。根据接头不低于被连接钢筋性能的原则,以800 ℃作为接头承载力明显下降的临界温度,既体现了该原则的存在性,又具有工程设计参考价值。
5 结论
基于上述理论分析、数据拟合、有限元仿真的结果,得到如下的结论:
(1) 根据套筒内部构造,套筒灌浆连接受力的失效模式包括两大类型:当套筒内表面存在凸肋等突起物时,发生套筒外钢筋断裂、套筒灌浆料与钢筋界面的黏结滑移失效中两种模式之一;当套筒内表面光滑时,发生套筒外钢筋断裂、套筒灌浆料与钢筋界面黏结滑移失效、套筒灌浆料与套筒界面黏结滑移失效中三种模式之一。
(2) 提出套筒灌浆连接承载力计算方法以及失效模式识别依据,并通过试验数据计算结果,建议单调递增受拉、反复拉压作用下的拟合系数分别取0.203、0.158,组合系数、整体系数均取1.2,但400 ℃高温作用后组合系数应取1.0。
(3) 通过套筒灌浆连接受力有限元仿真分析,捕捉到套筒外钢筋断裂失效过程及其模式,有助于套筒灌浆连接失效模式的精确识别。
(4) 套筒灌浆料抗压强度达到85.1 MPa、钢筋黏结长度达到7.7 倍钢筋直径时,套筒灌浆连接失效模式转变、承载力明显下降的临界温度分别为400 ℃、800 ℃。
