基于非定常气动力降阶的AGARD445.6 硬机翼不同迎角颤振研究

容浩然，戴玉婷，许云涛，杨 超

(北京航空航天大学航空科学与工程学院，北京 100191)

现代战斗机具备的高机动性，使之需要在大迎角条件下飞行；导弹机动时舵面处于大迎角状态；飞机在遇到阵风时机翼可能会进入较大的迎角状态；风力机叶片、涡轮叶片等机械部件通常也是在有稳态迎角状态工作。非零迎角状态机翼的颤振特性与零迎角时有一定区别，但传统的气动弹性试验以及计算研究通常采用零迎角，针对三维机翼不同迎角的气动弹性研究相对较少。ASHLEY[1]、EDWARD 等[2]、DOGGETT 等[3]和YATES 等[4]的研究表明：机翼迎角是跨音速段的颤振特性的重要影响参数，他们利用风洞试验、理论方法等研究了跨音速段迎角对颤振边界的影响，但以上研究都属于小迎角范围，且迎角对颤振边界的影响主要是由跨音速段气动非线性引起；YE 等[5]分别对矩形机翼和三角翼完成了不同迎角的颤振风洞试验；张伟伟等[6]和全景阁等[7−8]对比不同迎角下大后掠三角翼的气动弹性时域响应特性，研究了分离涡破裂前和破裂后三角翼的气动弹性稳定性特性，得到了有益规律；翼型小迎角经典颤振和大迎角失速颤振方面，叶正寅等[9]使用数值计算方法研究NACA0012 翼型在不同迎角下的颤振特性，发现到达某一迎角后，颤振边界突然下降；刘畅畅等[10]对NACA0012 翼型完成不同迎角的风洞试验，颤振结果与叶正寅流固耦合计算结果基本一致；LI 等[11]使用数值计算、循环神经网络降阶方法，研究了NACA64A010 二元翼段在跨音速小迎角范围内不同迎角的颤振边界；另外，TALLEY 等[12]针对AGARD445.6 软机翼，基于模态法使用数值计算、降阶模型方法分析不同迎角、来流马赫数下的气动弹性时域响应，发现迎角增加后，颤振边界降低。根据现有研究，在超过某一迎角后，机翼的颤振边界可能下降，因此，有必要对不同迎角下三维机翼的颤振特性进行研究。

气动弹性研究中，非定常气动力计算方法有ONERA 模型[13−14]、Leishman-Beddoes(L-B)模型[15]等。随着计算机技术的兴起，计算流体力学(Computational fluid dynamics, CFD)开始应用于各项工程和研究[16−17]。但是基于CFD 的流固耦合(Fluid-structure interaction, FSI)方法的非定常建模通常计算量大、计算时间长，因而需要发展高效、高精度的非定常气动降阶模型(Reduced order model, ROM)，快速、准确计算非定常气动力。非定常气动降阶方法主要包括系统辨识法和特征提取法，前者以自回归滑动平均法(AutoRegressive moving average, ARMA)、Volterra 级数、机器学习等为代表，后者以本征正交分解(Proper orthogonal decomposition, POD)、动力学模态分解(Dynamic mode decomposition, DMD)为代表。在各种非定常气动降阶方法中，人工神经网络(Artificial neural network, ANN)具有很强的非线性拟合能力[18]，且ANN 天然就具备对多输入/多输出系统的描述能力，这些优势使得近年来ANN 在非定常气动降阶领域应用非常广泛。MARQUES 等[19]建立了多层神经网络，分别以单俯仰运动为输入和俯仰运动、来流马赫数耦合输入，以翼型升力系数和力矩系数为输出，辨识跨声速段不同马赫数下二维翼型非定常气动力，由于只考虑了当前时刻输入与当前输出之间的关系，本质是一种定常模型；QIU等[20]建立了多层神经网络，把时间序列数据作为输入，预测了二维翼型的失速颤振；WINTER 等[21]基于反馈模糊神经网络建立了AGARD445.6 机翼变马赫数气动降阶模型，预测了不同马赫数下给定广义运动的广义力，快速计算频域气动力系数矩阵，然后使用pk 法研究了机翼跨音速颤振特性；王博斌等[22]建立了带反馈的径向基神经网络(Radial basis function neural network, RBFNN)气动降阶模型，辨识预测跨声速不同频率、不同振幅俯仰运动下二元翼段的气动特性；KOU 等[23]在此基础上其与自回归(AutoRegressive eXogenous,ARX)方法并联得到混合降阶模型；LI 等[24]和KOU 等[25]建立了长短时记忆单元(Long short-term memory, LSTM)循 环 神 经 网 络(Recurrent neural network, RNN)，考虑跨音速条件下，以俯仰、沉浮耦合和马赫数作为输入，辨识预测了不同马赫数下翼段气动特性，并将气动降阶模型用于颤振特性预测。目前的非定常气动降阶研究中，研究对象大多针对零迎角刚性翼型，针对非零迎角三维弹性机翼的非定常气动降阶研究较少。

本文首先介绍了基于模态叠加的流固耦合方法、基于RBFNN 的非定常气动力ROM 建模方法和两种基于降阶模型的颤振预测方法；针对AGARD445.6 硬机翼[26]，完成不同初始迎角流固耦合颤振计算，总结了随着初始迎角增加颤振边界变化规律；选取10°初始迎角条件，建立基于RBFNN 的非定常气动力ROM，预测不同速度、减缩频率的非定常气动力，预测10°迎角的颤振特性；基于10°迎角非定常气动降阶建模的研究结果，建立考虑初始迎角输入的非定常气动力ROM，快速预测机翼不同迎角的颤振特性；最后基于建立的ROM 分析颤振边界随迎角变化的机理。

1 计算方法

1.1 基于模态叠加的流固耦合方法

多自由度线性系统受迫振动方程为：

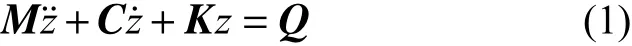
式中：M、C、K分别为系统的质量矩阵、阻尼矩阵、刚度矩阵；z为多自由度系统真实位移；Q为外部作用力。系统真实位移可以表示为广义坐标的线性叠加：

式中：Φ 为结构质量归一模态；d为广义坐标，则式(1)可化为：

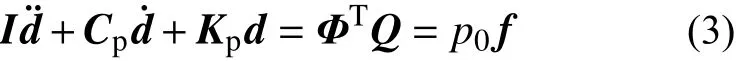
式中：I、Cp、Kp分别为广义质量矩阵(单位阵)、广义阻尼矩阵、广义刚度矩阵(对角阵且对角元素为固有角频率平方)；p0为来流动压；f为时域广义力系数。气动弹性系统中通常忽略结构阻尼，则式(3)的微分方程组解耦。通过施加初始广义速度扰动d˙0，使用CFD 方法求解气动力Q，采用四阶龙格-库塔方法求解此微分方程组，即可得到该初始条件下的气动弹性时间响应。

在流固耦合计算中引入假设：只考虑垂直于机翼所处平面方向的变形，即机翼处于xoy平面，模态只考虑z方向分量。该假设在静变形和动态变形不太大时是合理的。

在计算具有初始迎角机翼的气动弹性响应时，应先计算该迎角下的静气动弹性变形，在静气动弹性计算收敛后施加广义速度扰动，得到动气动弹性时间响应，具体步骤如下：

1)给系统施加阻尼，计算式(3)直至收敛得到静气弹结果；

2)在静气弹的基础上施加广义速度扰动d˙0，同时取消阻尼，计算式(3)得到动气弹时域响应。

RBFNN 由BROOMHEAD 等[27]提出，其结构包含三层：输入层、隐含层和输出层，其中隐含层的激活函数为径向基函数，输入靠近基函数中心点时神经元才会被激活，输出层激活函数为线性函数。典型的RBFNN 结构如图1 所示。

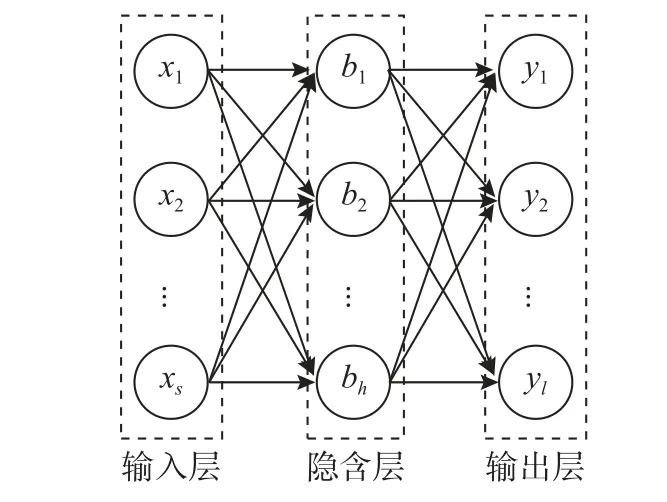
图1 径向基神经网络结构Fig. 1 Structure of RBFNN

1.2 基于径向基神经网络的非定常气动降阶方法

式中：隐含层的激活函数一般为高斯基函数，bv为隐含层第v个神经元输出；cv为第v个神经元的中心向量；σv第v个神经元的宽度。隐含层到输出层为线性变换：

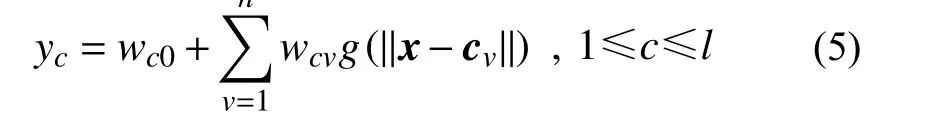
式中：yc为输出层第c个输出；wcv为隐含层第v个神经元到输出层第c个神经元的权重。RBFNN 训练过程中，在隐含层神经元个数、基函数、中心向量和宽度确定后，权重的学习仅需求解线性方程，因而RBFNN 相比于传统多层前馈神经网络结构简单、训练成本低、收敛速度快。另外，只要隐含层数量足够大，RBFNN 能以任意精度逼近非线性函数。

RBFNN 一般有两种：正则RBFNN 和广义RBFNN。正则RBFNN 的隐含层数量与训练样本量相同，隐含层中心向量与对应的输入向量相同，正则RBFNN 通常足够精确，但考虑本文的问题，输入样本量较大导致神经网络结构庞大，可能导致训练困难、矩阵出现病态，训练结果可能过拟合；本文选择建立的广义RBFNN，则是逐个添加隐含层神经元，直到均方误差达到设定要求，建立的模型则为满足误差要求的最简RBFNN 结构，详细步骤为：

1)用神经网络拟合训练样本，得到训练样本中误差最大的输入向量；

2)增加隐含层神经元，其中心向量为上述误差最大的输入向量；

3)优化权重矩阵，返回步骤1)，直到均方误差达到设定要求或隐含层神经元数量达到设定上限。

1.3 基于气动降阶模型的颤振预测方法

在有初始迎角的气动弹性分析中，广义位移、广义力均可以表示为静气弹量和相对于静气弹量的叠加，即 ξ=ξs+ξt，其中：ξ 为广义位移、广义力、广义力系数；下角标s 为静气弹量；下角标t 为相对于静气弹量。因此，颤振方程式(3)可以表示为：

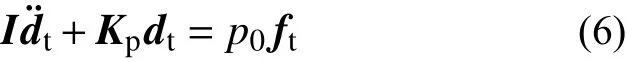
为了描述方便，若无特别说明，后续所述广义位移、广义力、广义力系数等均为相对于静气弹量，并省略下角标t。本文基于非定常气动力ROM 的颤振预测涉及两种方法，时域下的龙格库塔法(RK 法)和频域下的VG 法[28]。

RK 法中，使用降阶模型预测颤振方程式(6)中的广义力系数f，设定初始条件，使用四阶龙格库塔方法数值求解方程式(6)，即可得到气动弹性时域响应。

VG 法中，临界稳定的颤振方程可以化为式(7)。定义减缩频率和无量纲来流速度，即减缩速度如式(8)：

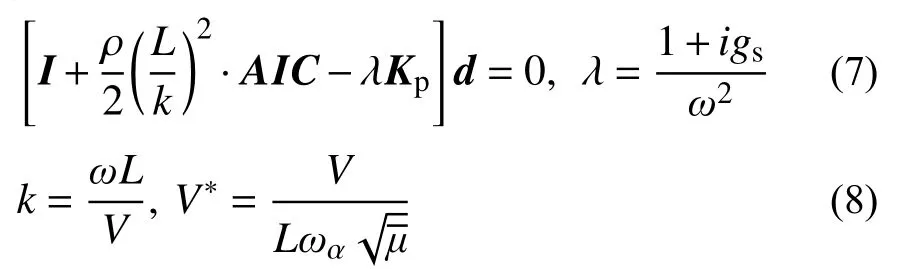
式中：L为参考长度；ρ 为密度；V为来流速度；ωα为扭转模态角频率；μ为质量系数；AIC为频域气动力系数矩阵；gs为阻尼；ω为结构运动角频率。AIC与减缩频率和来流速度有关，因为机翼在大迎角时速度的改变会改变机翼的静变形位置，从而对非定常气动特性产生影响，进而影响AIC矩阵。通过降阶模型预测某一减缩频率、速度下的时域广义力系数，再将结果转化到频域，即可得到该减缩频率、速度下的AIC矩阵。基于降阶模型，使用VG 法预测某一迎角颤振特性的步骤为：

1)给定一系列速度输入V*，计算该速度下的AIC。

2 基于流固耦合的数值算例与结果分析

2.1 流固耦合方法验证

使用ANSYS Fluent 软件进行气动力计算。首先验证SA 湍流模型计算分离流的适用性，选取一大后掠角三角翼模型VFE-2[29]，三角翼前缘后掠角为65°，平均气动弦长为0.436 m，展长为0.610 m，模型详细几何参数见参考文献[29]。其前缘可以更换，本文选取带尖前缘的VFE-2 三角翼模型。计算条件为雷诺数6×106、来流马赫数0.4、迎角13.3°，网格如图2 所示，网格数量1.13×106，最大y+为24。计算不同展长截面的压力系数分布，与试验结果对比后发现趋势基本一致，如图3 所示。

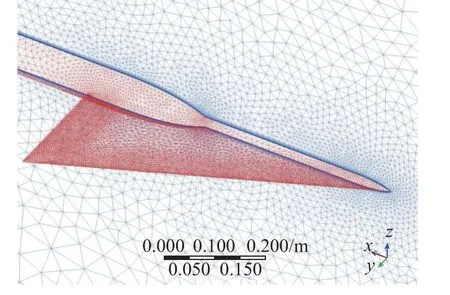
图2 VFE-2 计算网格Fig. 2 Mesh distribution of VFE-2

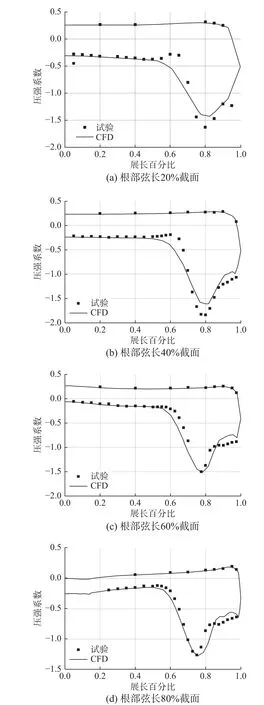
图3 不同截面压强系数分布CFD 与试验对比Fig. 3 Pressure coefficient at various sections by CFD and experiment

AGARD445.6 机翼展长为0.762 m，参考长度L取根部半弦长0.28 m，机翼详细几何参数见参考文献[21]。计算网格采用六面体网格划分，如图4所示，网格数量为1.38×106，第一层网格厚度为10−5m 量级，动网格变形方法为扩散光顺，湍流模型采用SA 模型，时间步长0.0002 s。选取来流马赫数0.451，迎角10°，使用上述网格(最大y+为25)和细网格(最大y+为6)计算机翼90%展长处的压强分布如图5，同时计算翼面法向力系数(垂直翼面方向)对比如表1，可以发现两套网格计算结果基本相同，这是由于ANSYS Fluent 软件中对SA 模型进行了y+去敏感化处理[30]。为了节省计算量并避免出现动网格负体积问题，使用最大y+为25 的网格进行后续计算。

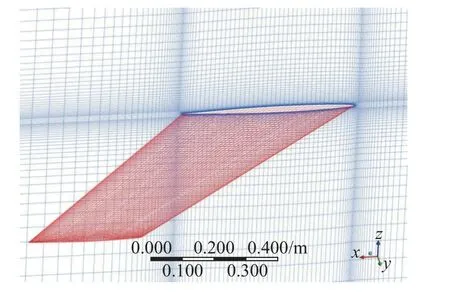
图4 AGARD445.6 计算网格Fig. 4 Mesh distribution of AGARD445.6 wing

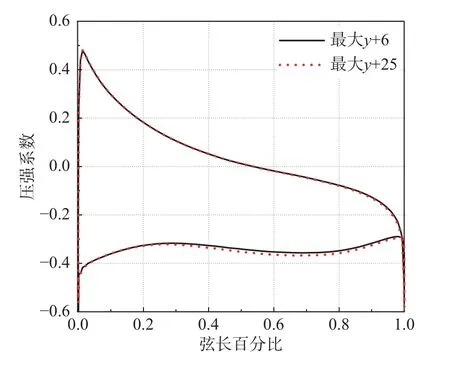
图5 迎角10°90%展长处压强系数分布对比Fig. 5 The comparison result of pressure coefficient at 90%span and angle of 10°

表1 迎角10°法向力系数Cn 对比Table 1 The comparison result of normal force coefficient Cn at angle of 10°

然后，采用文献[21]的AGARD445.6 软机翼3 号模型的颤振试验数据验证流固耦合方法。由于机翼颤振形式为前两阶模态耦合，计算取用前两阶模态，频率如表2。编写用户自定义函数(User defined functions, UDF)完成流固耦合数值仿真。选取来流马赫数0.499、空气密度为0.428 kg/m3的风洞试验条件进行0°颤振计算，通过改变大气压强和温度，保证密度不变的同时改变来流速度，不同条件下求得两阶模态的广义位移响应如图6。最终本文计算得到颤振速度与文献试验结果[26]对比如表3，本文采用的流固耦合方法计算结果与试验结果基本一致。

表3 试验与流固耦合计算结果对比Table 3 Flutter results of CFD and experiment

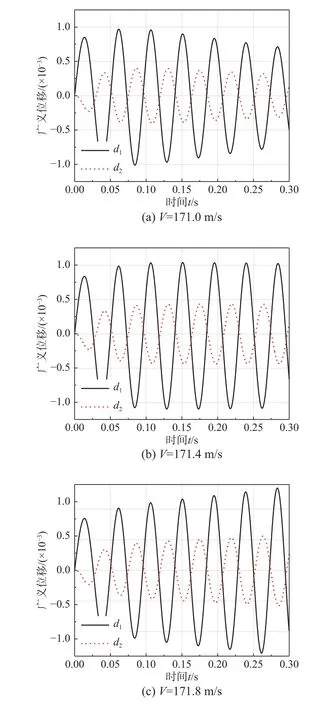
图6 0°迎角不同来流条件广义位移响应Fig. 6 Time responses of wing tip displacement at various velocities (angle of 0°)

表2 AGARD445.6 软机翼前两阶模态频率Table 2 Mode frequency of AGARD445.6 weakened wing

2.2 不同初始迎角下的机翼颤振边界规律

本节计算机翼0°～10°迎角的颤振特性。由于软机翼在大迎角下静变形过大不符合本文假设，使用硬机翼模型进行后续研究，前两阶模态频率如表4[26]。

表4 AGARD445.6 硬机翼前两阶模态频率Table 4 Mode frequency of AGARD445.6 solid wing

选取来流马赫数0.451、空气密度1.113 kg/m3。为了减少计算量的同时便于得到迎角与颤振特性的规律，本文设计了不同速度和初始迎角的计算状态点，计算得到的颤振特标准差误差棒如图7所示。通过计算每个状态点的广义位移时域响应即可得到该迎角下颤振边界和颤振频率范围，以10°迎角为例，通过数值仿真计算发现V*=0.459 时响应收敛、V*=0.472 时响应发散，如图8 所示，则10°迎角的颤振边界和颤振频率比在两者之间。从图7 中不同状态的颤振计算结果中可以看出，在迎角0°～7°，颤振边界减小，而7°～10°初始迎角时颤振边界反而增加。

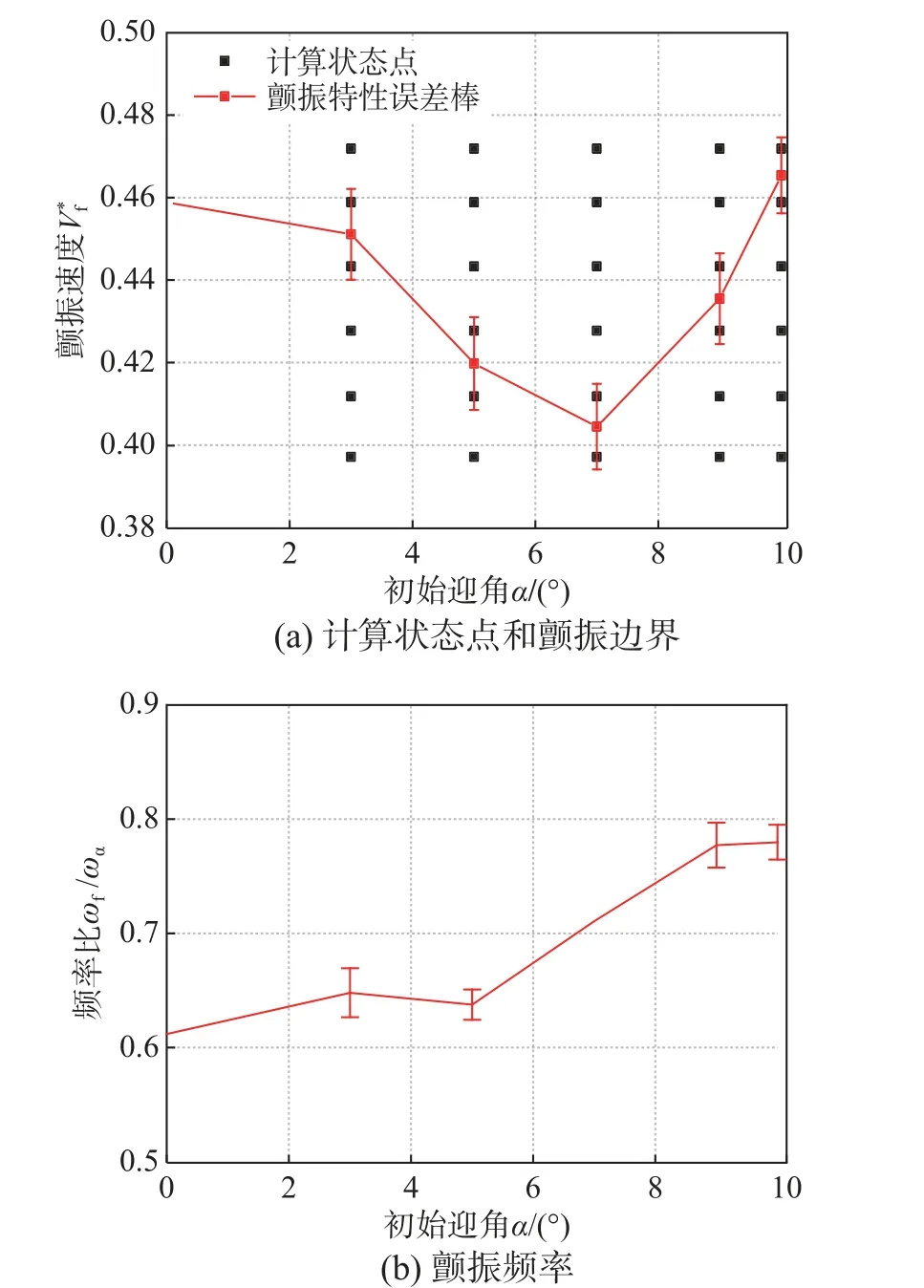
图7 计算状态点和颤振特性标准差误差棒Fig. 7 Calculation conditions and standard error bar of flutter boundary and frequency ratio

图8 10°迎角不同来流条件广义位移时域响应Fig. 8 Aeroelastic responses at different reduced velocities (angle of 10°)

3 基于降阶模型的颤振预测与结果分析

3.1 10°迎角气动降阶与颤振预测

机翼在大迎角时，速度的不同会影响机翼的静变形量，从而导致非定常气动力特性的改变。为了探究ROM 中速度输入的影响，在10°迎角条件下建立两种气动力ROM：ROM1 仅有广义位移输入，不考虑速度的输入，输入输出形式如式(9)；ROM2以速度和广义位移为输入，输入输出形式如式(10)。

式中：fij为第j阶广义运动引起的第i阶时域广义气动力系数；Δt为时间步长；n为时间步延迟数；m为样本量。

静气弹基础上设计正弦叠加形式广义位移的训练信号如式(11)：

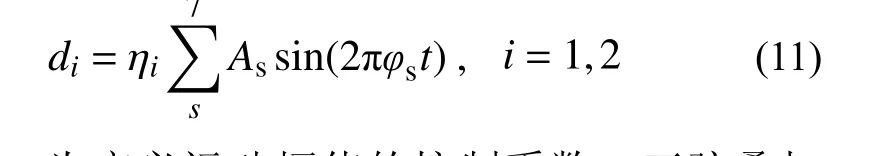
式中：ηi为广义运动幅值的控制系数；正弦叠加的幅值As为随机数；频率φs从5 Hz 开始，间隔10 Hz 直到65 Hz。分别给定两阶训练信号，计算1000 个时间步，对应的广义力系数作为ROM1 训练集。ROM1 训练信号图像如图9。

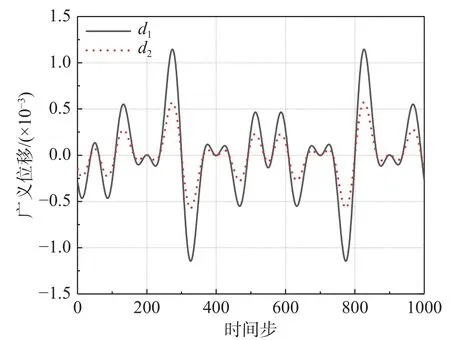
图9 ROM1 训练信号Fig. 9 Training signal of ROM1

ROM2 的训练集中，选取4 个速度条件，在不同速度下，分别给定各阶广义位移以式(11)的训练信号，计算对应的广义力系数作为ROM2 训练集。由于给定了4 个速度阶梯，ROM2 训练集的CFD 计算量为ROM1 的4 倍。ROM2 训练信号和速度条件如图10。

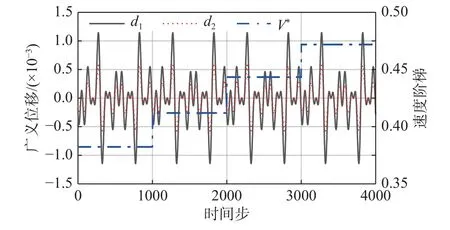
图10 ROM2 训练信号Fig. 10 Training signal of ROM2

设计不同速度、减缩频率条件正弦形式广义位移测试信号，并得到频域广义力系数矩阵AIC作为测试集。由于大迎角下存在的气动力非线性，测试信号的正弦运动选取小幅值以减少气动力非线性对频域广义力系数矩阵AIC和颤振特性预测的影响，一阶广义运动幅值取0.0003，二阶广义运动幅值取0.0002。两种ROM 训练集和测试集包含的减缩频率、速度信息如图11，测试集中，选取了4 个训练集范围外的减缩频率和速度条件，测试降阶模型的泛化能力。

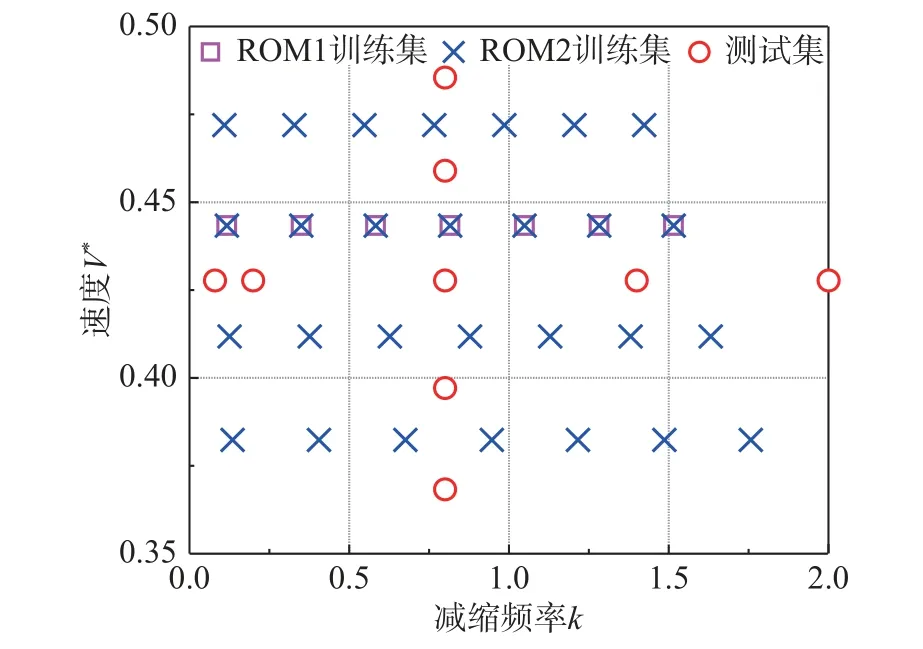
图11 训练集、测试集包含的减缩频率、速度信息Fig. 11 Ranges of reduced frequencies and reduced velocities of training data set and test data set

两种ROM 辨识结果如图12 和图13，辨识误差如表5，其中定义误差e为式(12)的形式，其中：yCFD为CFD 计算结果向量；yROM为降阶模型计算结果向量。

图12 ROM1 辨识结果Fig. 12 Identification results of ROM1

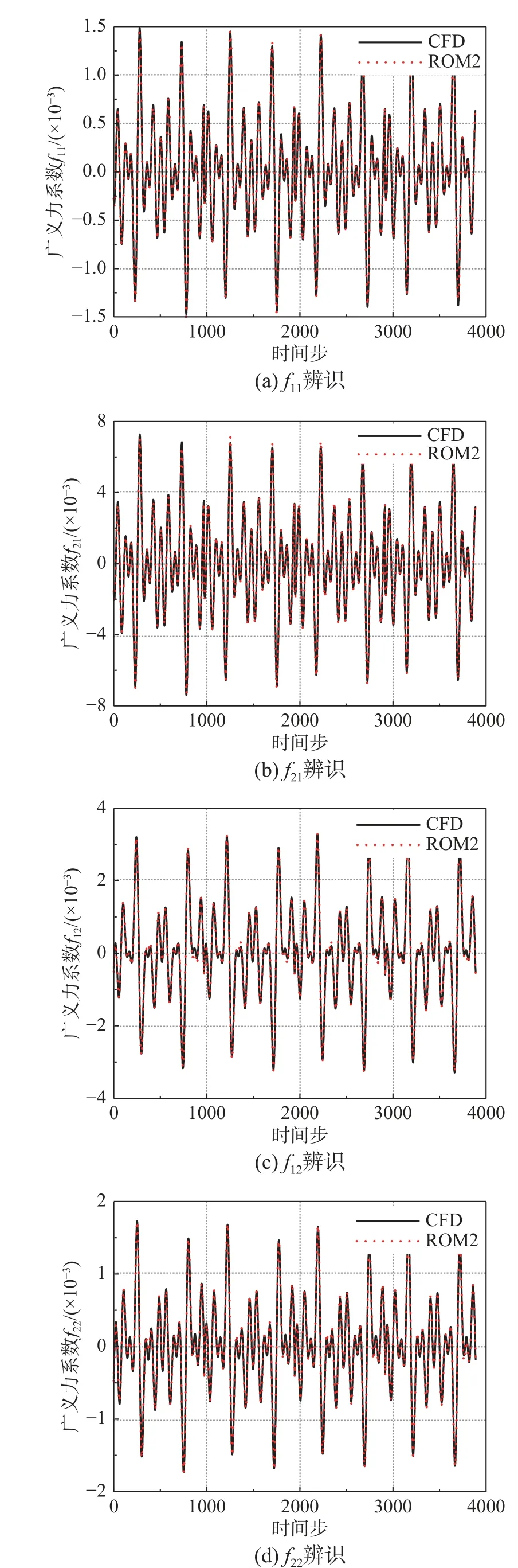
图13 ROM2 辨识结果Fig. 13 Identification results of ROM2

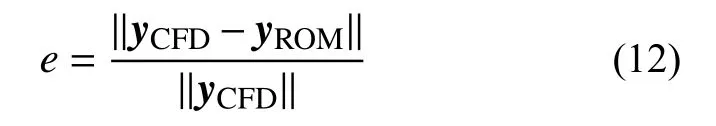
表5 ROM1 和ROM2 辨识误差Table 5 Identification error of ROM1 and ROM2

使用得到的两种ROM，预测速度V*=0.428，不同减缩频率下的频域气动力系数矩阵AIC，并与预测集CFD 计算结果对比如图14，速度不变时，两种降阶模型预测集结果均与CFD 计算结果基本一致，且训练集之外部分的预测结果也较好，证明了ROM 的泛化能力；基于两种ROM 预测减缩频率k=0.4，不同速度下的频域气动力系数矩阵AIC，并与预测集CFD 计算结果对比如图15，显然ROM2 的预测与CFD 结果吻合更好。

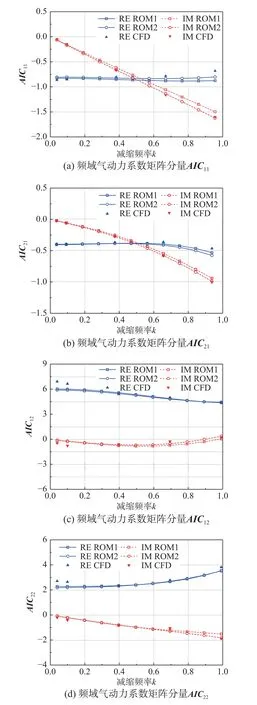
图14 V*=0.428，不同减缩频率k 的AIC 分量Fig. 14 AIC components at V*=0.428 and various reduced frequencies

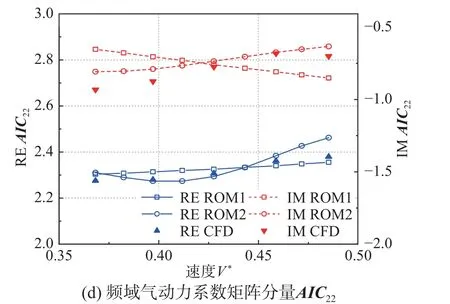
图15 k=0.4，不同速度V*的AIC 分量Fig. 15 AIC components at k=0.4 and various reduced velocities

基于建立的两种ROM，使用RK 法和VG 法的颤振预测如图16～图19，颤振预测结果对比如表6 所示，结果仍然是ROM2 的颤振边界预测精度更高，且能较准确的预测不同速度下的广义位移时域响应。可以看出，考虑速度输入的ROM2的不同速度的AIC预测和颤振预测精度更高，但增加速度输入后，ROM 训练集需要的CFD 计算代价也将大量增加；不考虑速度输入的ROM1 虽然不同速度的AIC预测和颤振预测误差相对较大，但是训练集需要的CFD 计算代价较低。另外，RK 法和VG 法预测结果基本一致。

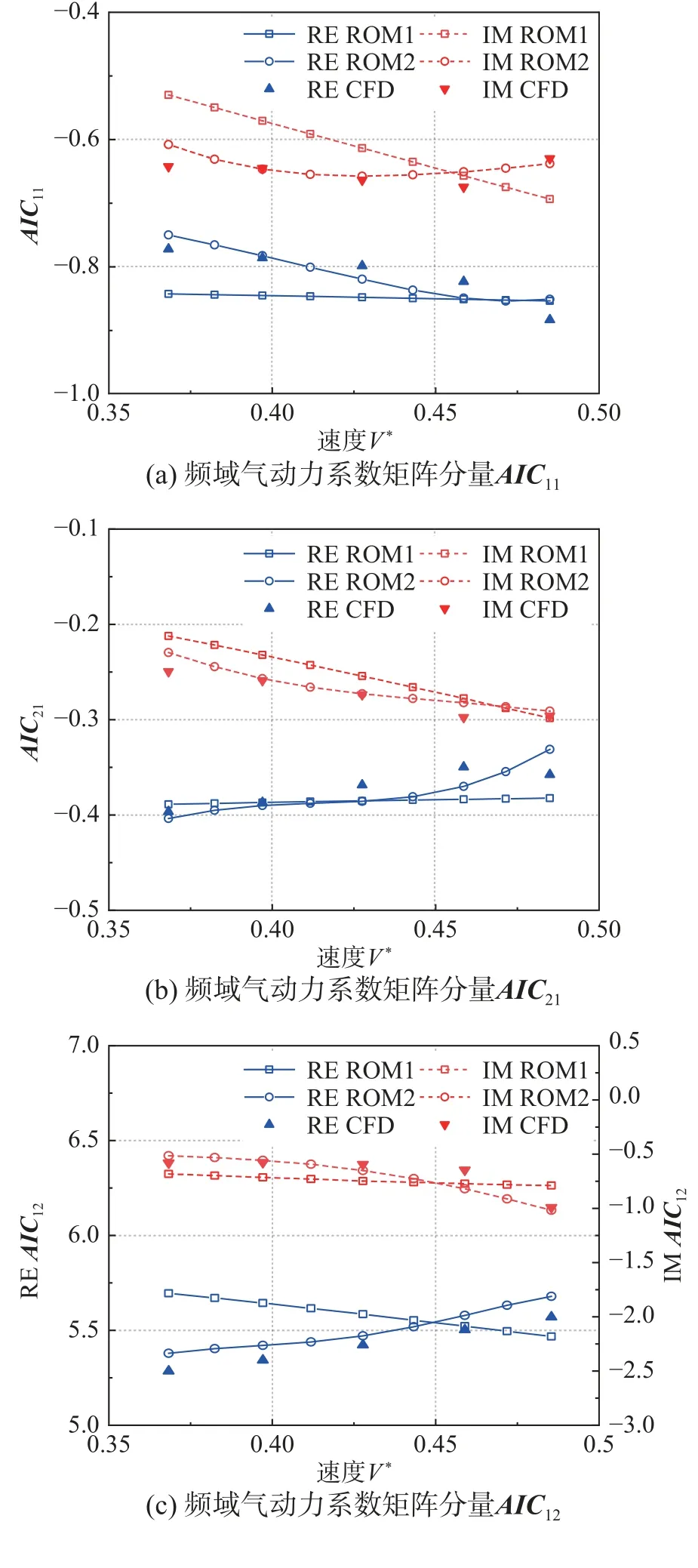
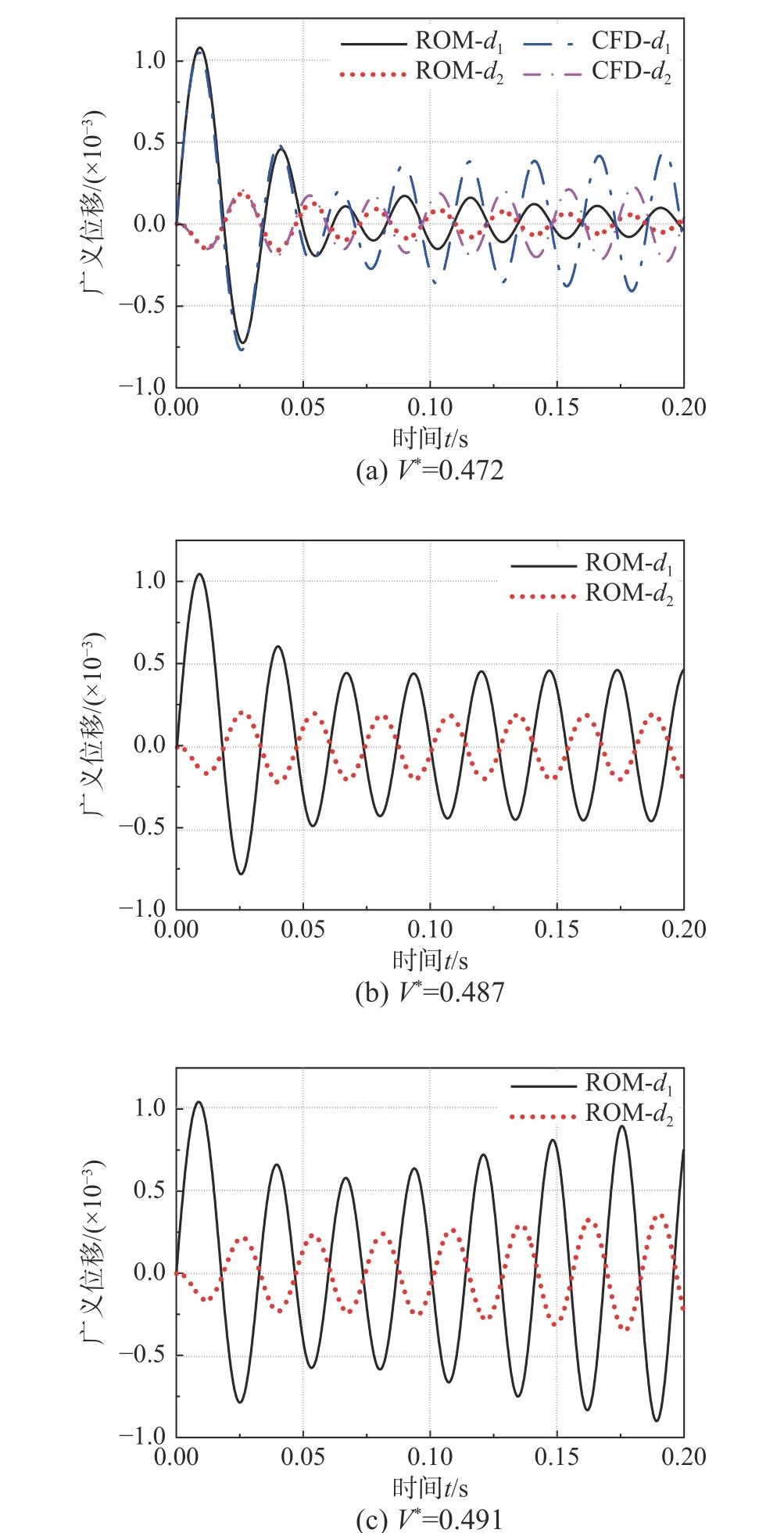
图16 基于ROM1，RK 法的颤振预测Fig. 16 Flutter prediction by ROM1, RK method

图17 基于ROM2，RK 法的颤振预测Fig. 17 Flutter prediction by ROM2 and RK method

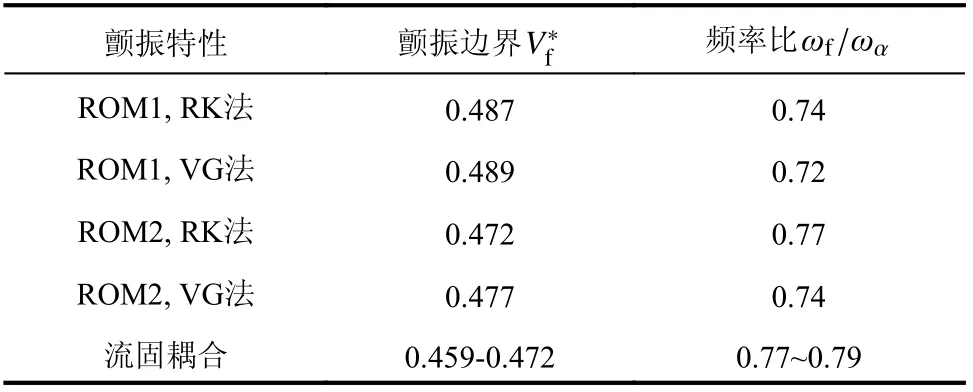
表6 基于降阶模型的10°迎角颤振预测与流固耦合对比Table 6 Flutter prediction by ROM and FSI, α = 10°

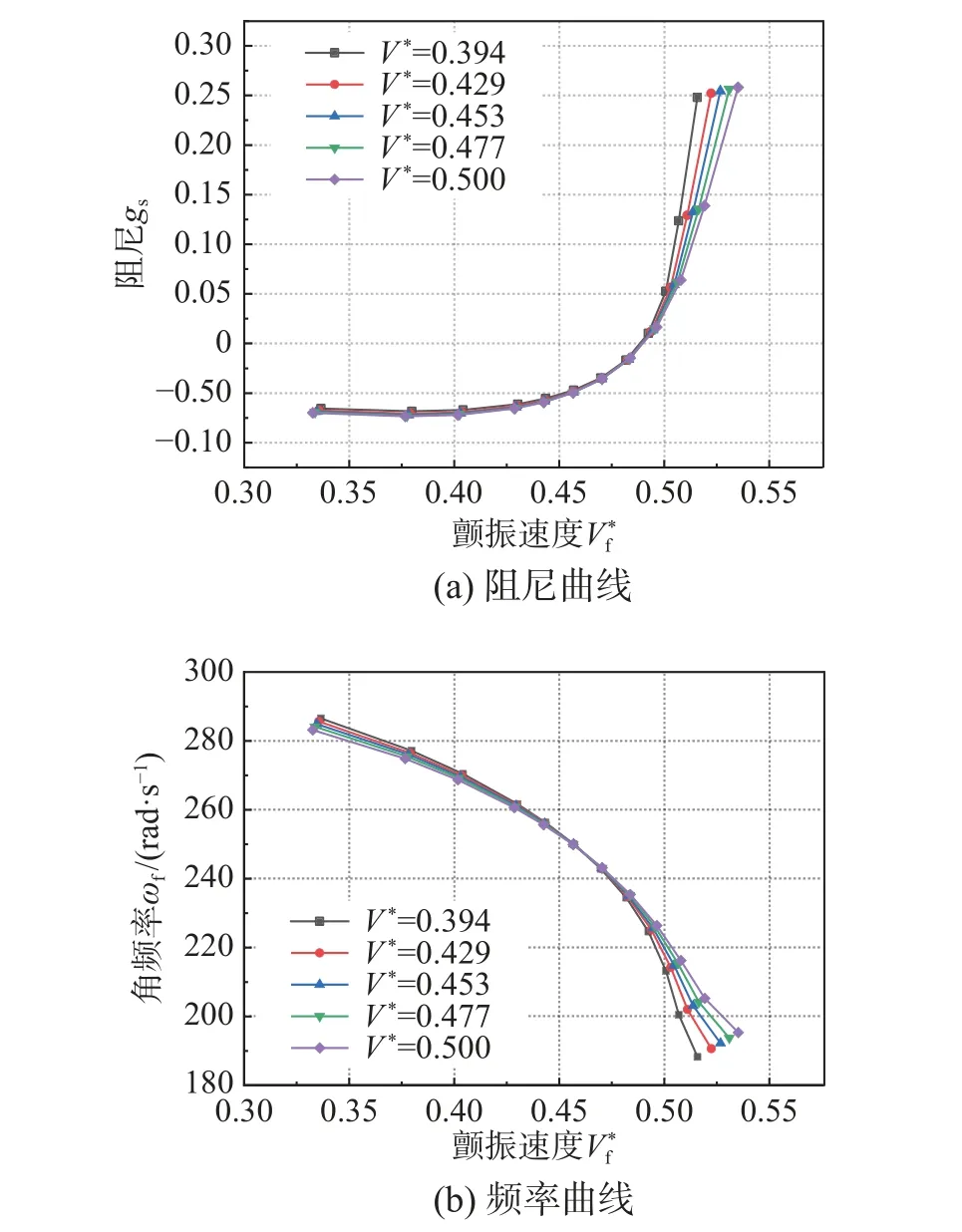
图18 基于ROM1，VG 法的颤振预测Fig. 18 Flutter prediction by ROM1 and VG method

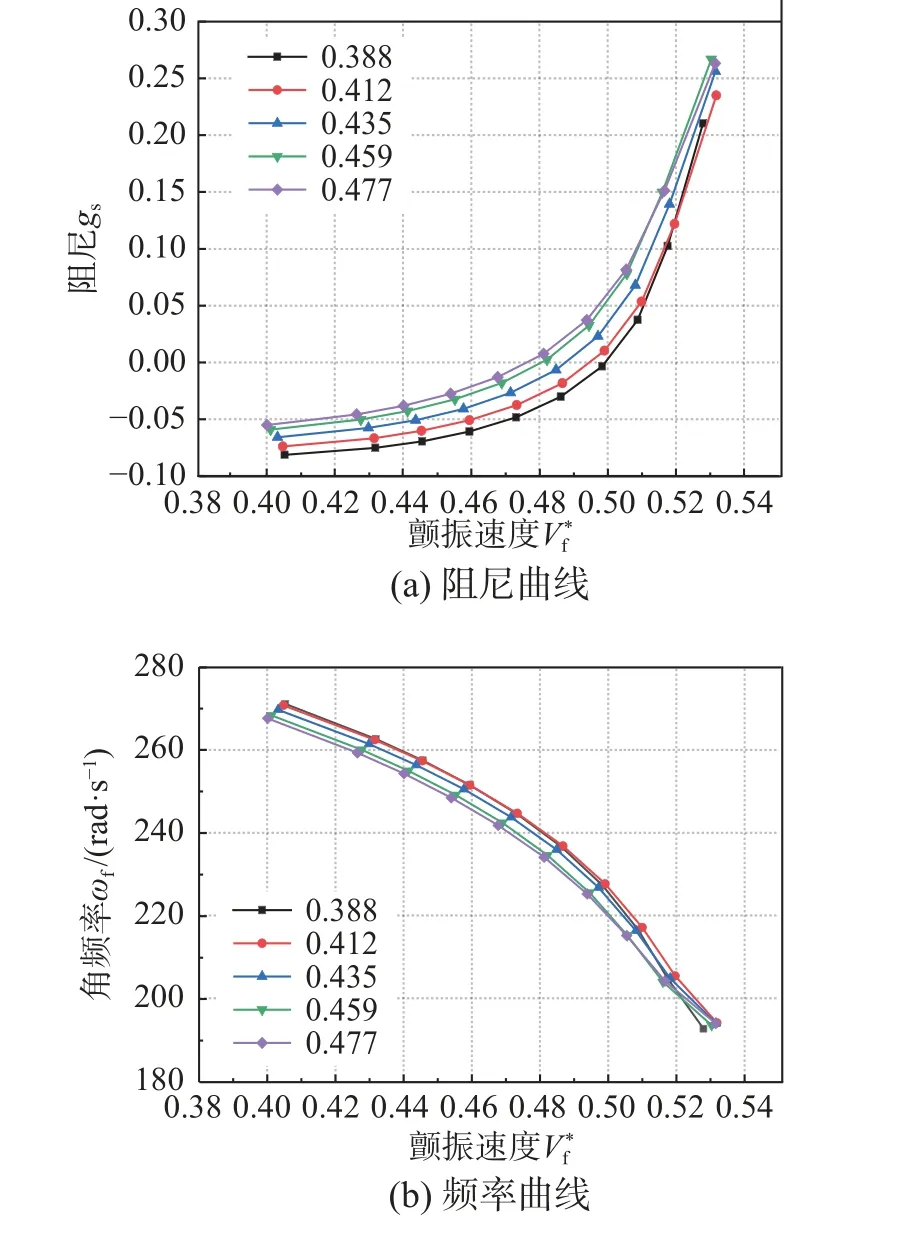
图19 基于ROM2，VG 法的颤振预测Fig. 19 Flutter prediction by ROM2 and VG method

3.2 考虑初始迎角输入的气动降阶与颤振预测

为了进行不同迎角的颤振预测和颤振特性分析，需要建立考虑初始迎角α 输入的非定常气动力ROM。为了降低CFD 计算量同时得到定性正确的规律，降阶模型ROM3 输入为不同时间步的广义位移和初始迎角，而不考虑速度输入，输入形式如式(13)。

为了对迎角7°颤振边界拐点附近的非定常气动力特性进行更精细的建模，ROM3 分为两部分：ROM3A 模 型 的 迎 角 输 入 为[0°, 2°, 4°]，ROM3B 模型的迎角输入为[4°, 6°, 8°, 10°]。后续使 用ROM3A 完成迎 角[0°, 1°, 2°, 3°, 4°]、使用ROM3B 完成迎角[4°, 5°, 6°, 7°, 8°, 9°, 10°]的频域气动力系数矩阵AIC和颤振预测。广义位移训练信号依然采用式(11)，训练信号和初始迎角条件如图20 所示；测试集选择计算减缩频率k=0.4，迎角α=[0°, 3°, 5°, 7°, 10°]下的频域气动力系数矩阵AIC。训练集、测试集计算的速度V*=0.443。降阶模型的辨识误差如表7 所示。

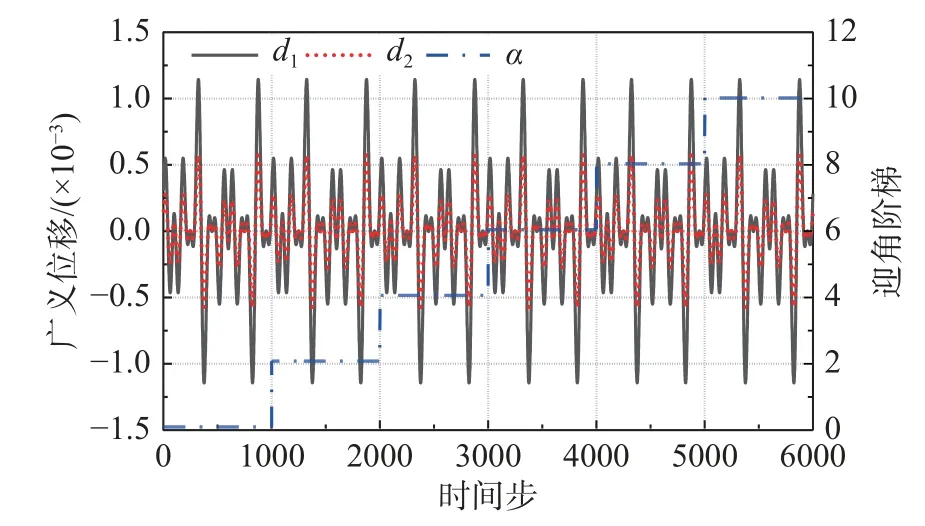
图20 ROM3 训练信号Fig. 20 Training signal of ROM3

表7 ROM3 辨识误差Table 7 Identification error of ROM3

基于ROM3 预测速度V*=0.443，减缩频率k=0.4，不同初始迎角下的频域气动力系数矩阵AIC，并与测试集CFD 计算结果对比如图21，ROM3 能准确预测AIC随迎角变化的规律；使用RK 法和VG 法预测得到的不同迎角颤振特性如图22 所示，两种预测方法的结果基本一致。虽然随着迎角的增加，来流速度对机翼静变形量的影响增大，但ROM3 预测的颤振边界随迎角变化趋势与流固耦合结果基本一致，说明ROM3 虽然没有考虑速度输入，但仍能得到正确的颤振边界变化规律。之后ROM3 将用于迎角对颤振特性影响的机理分析中。

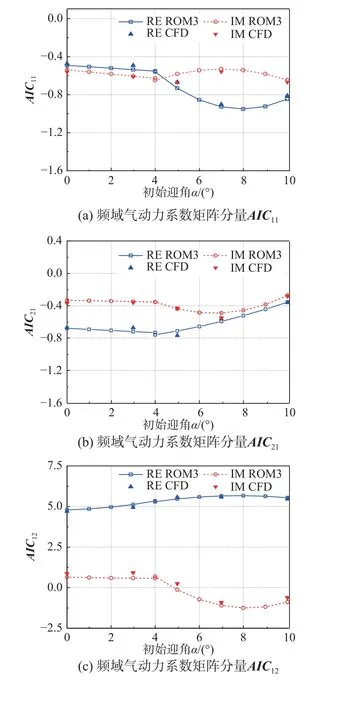
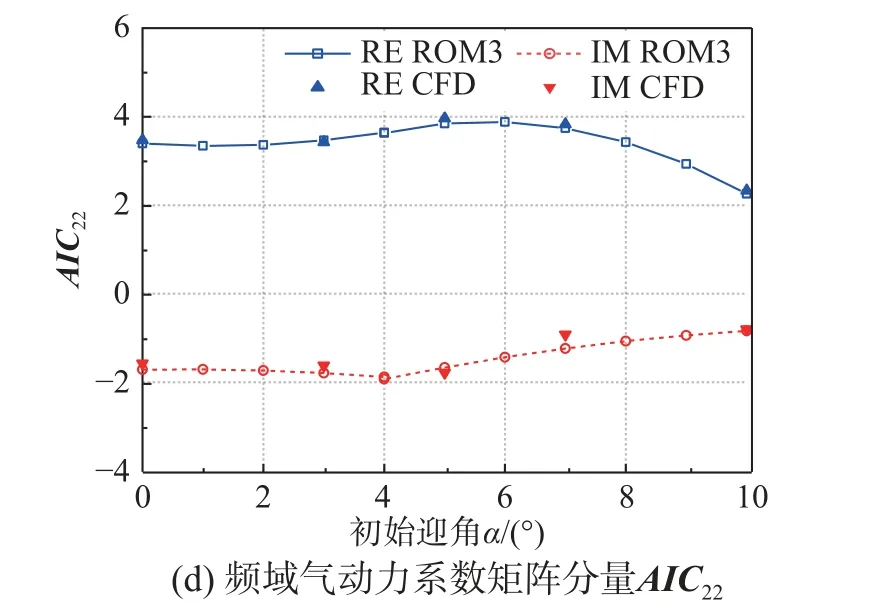
图21 k=0.4，V*=0.443，不同迎角α 的AIC 分量Fig. 21 AIC components at k=0.4, V*=0.443 and various angles of attack

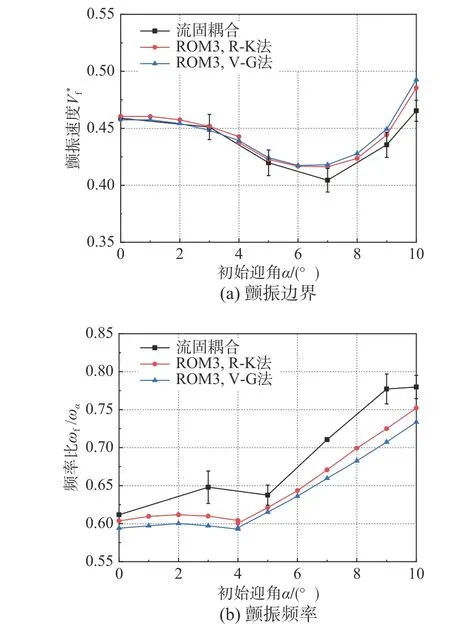
图22 不同迎角ROM3 颤振预测与流固耦合结果对比Fig. 22 Flutter prediction by ROM3 and CFD at various angles of attack

4 迎角对颤振边界影响的机理分析

将图21 中ROM3 预测的频域气动力系数矩阵AIC转化为时域广义力系数fij，其与广义位移dj的幅值比和相位差随迎角的变化规律如图23 所示。发现5°迎角内，相位差基本不变，广义力系数的幅值比随迎角的增加略有增大；7°迎角后，随着迎角的增加，4 个广义力系数的相位差开始变化，而广义力系数f21和f22的幅值比下降。即迎角小于5°时，静气弹基础上的相同运动下，广义力的幅值随迎角增加略有增大；迎角大于7°后，静气弹基础上的相同运动下，二阶广义力的幅值随迎角增加开始下降。

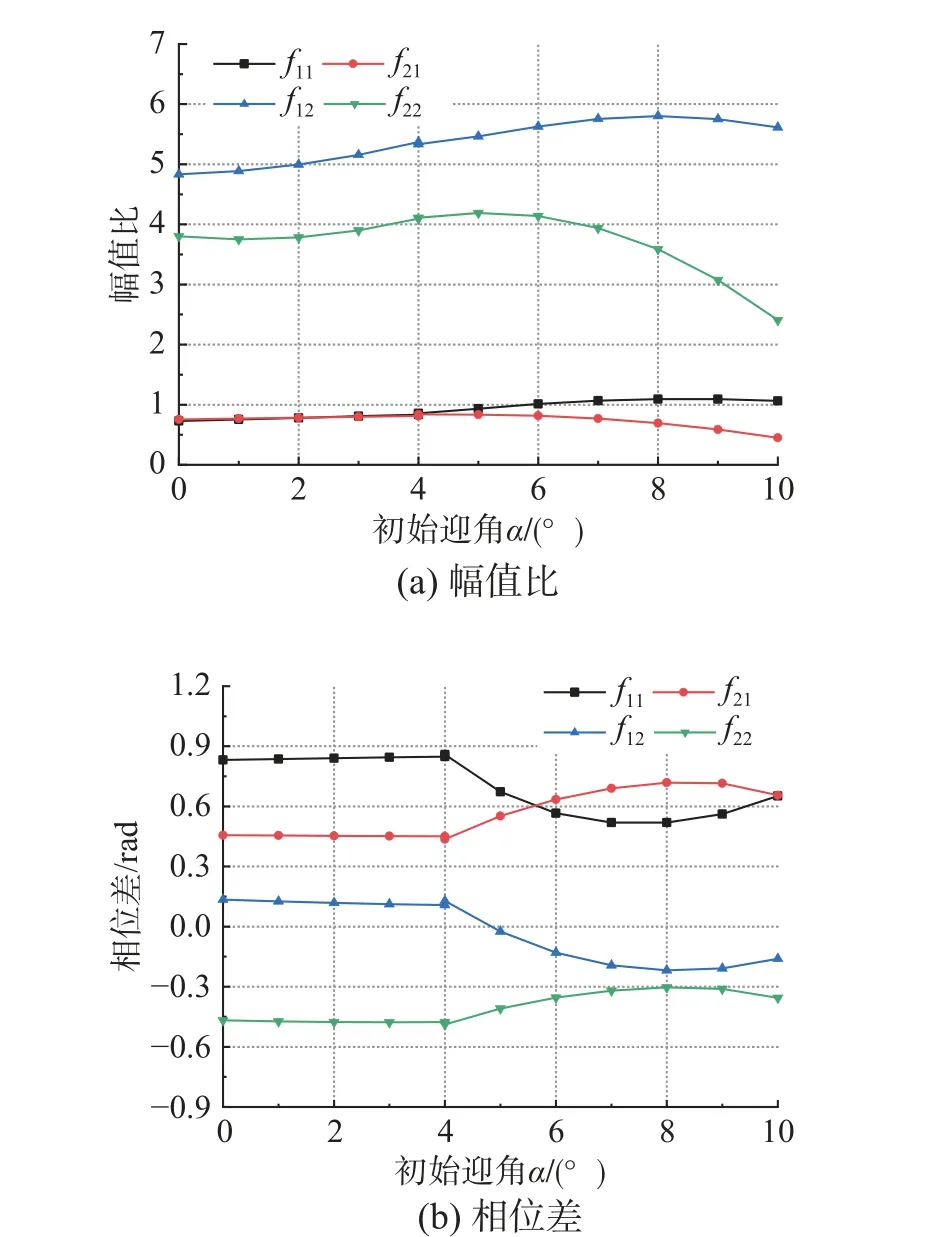
图23 k=0.4，V*=0.443，不同迎角α 下的广义力系数fij 与广义位移dj 的幅值比和相位差Fig. 23 Amplitude ratio and phase between general force coefficient and general displacement at k=0.4, V*=0.443 and various angles of attack by ROM3

为了探究上述规律的原因，选取来流马赫数0.42，迎 角0°、5°、7°、10°，速 度V*=0.427 的状态进行研究。后三个非零迎角条件下，静气弹收敛后的机翼上表面压强云图和流线图如图24 所示。可以发现5°迎角前机翼表面基本为附着流；随着迎角的增加，展向涡导致机翼上表面的分离区范围扩大，改变了上翼面的压强分布。然后在静气弹基础上分别给予两阶模态相同幅值、减缩频率k=0.42 的正弦运动。得到的广义力系数fij可以表示为式(14)：

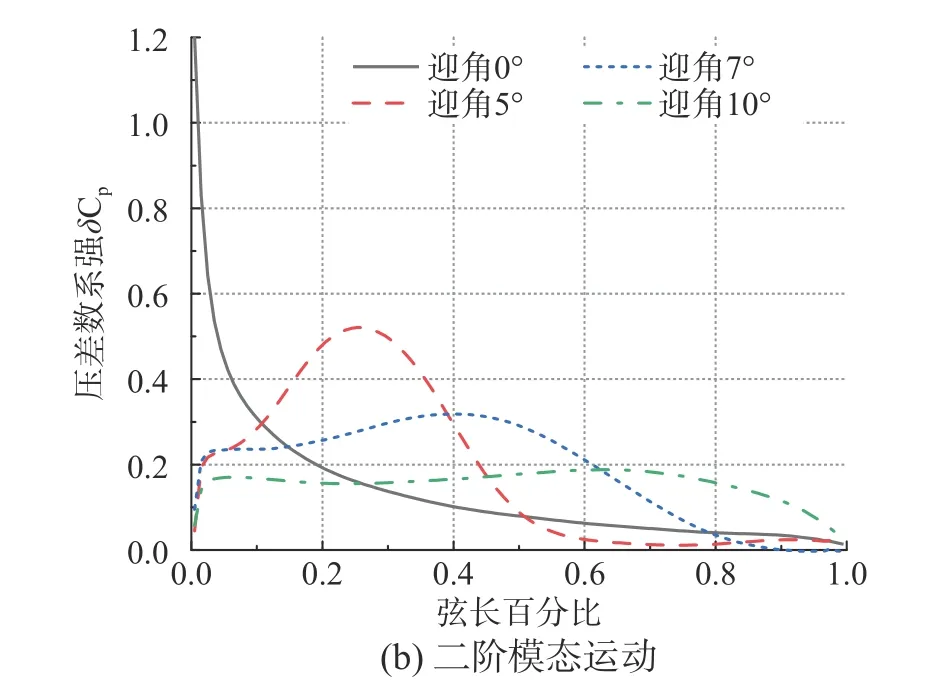
图24 机翼上表面压强云图和流线图Fig. 24 Pressure contour and streamline of the upper surface of the wing

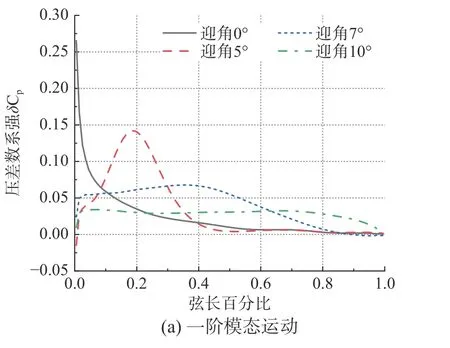
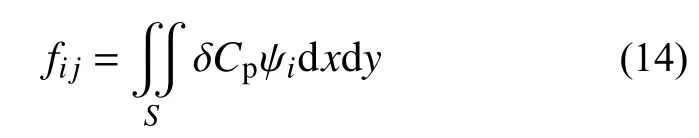
式中：ψi为第i阶模态的z方向分量；S为面积；δCp为相对于静气弹的上下翼面压强系数之差。在分别给两阶模态正弦运动后，选取广义力系数正弦的第一个峰值时刻，对比展向90%截面的δCp弦向分布如图25 所示。可以看出，小迎角时δCp主要集中于前缘，随着迎角的增加运动引起的δCp逐渐后移；大迎角后展向涡出现，导致δCp逐渐平均到整个翼弦。

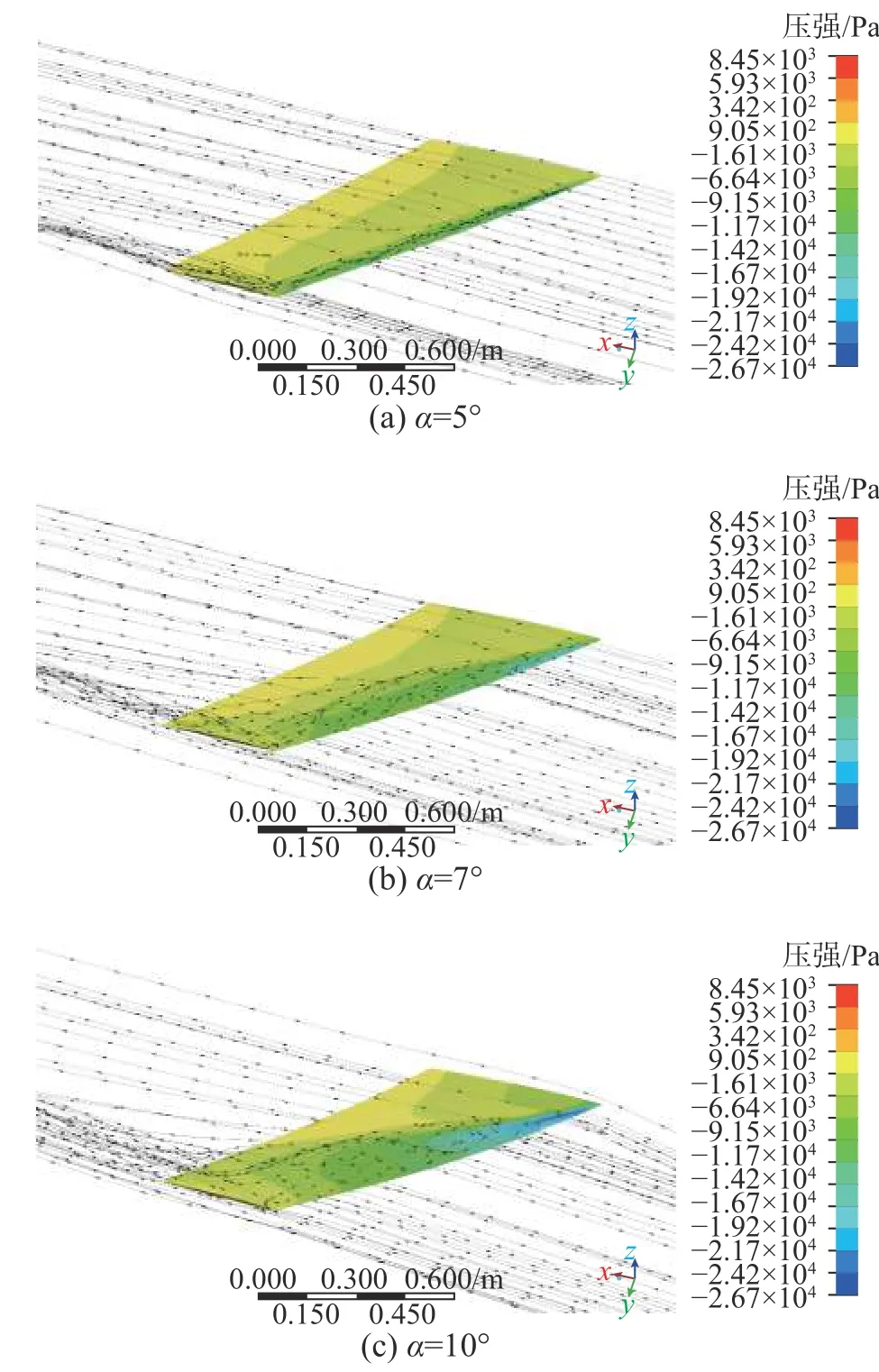
图25 不同迎角展向90%截面的δCp 弦向分布Fig. 25 δCp distribution at 90% span section for different angles

δCpψi体现了第i阶广义力系数在翼面上的分布，其于90%展长截面的弦向分布如图26 所示。可以发现，5°迎角前广义力系数分布与δCp分布类似，随着迎角的增加，其分布逐渐后移；5°迎角后，由于弯曲模态ψ1为正值，一阶广义力系数分布皆为正，而扭转模态ψ2沿弦向从正到负，导致二阶广义力系数分布出现负值。经过式(14)积分后得到该截面不同迎角的广义力系数如图27 所示。随着迎角的增加，小迎角时截面广义力系数略有增加，大迎角时截面二阶广义力系数f21和f22下降。

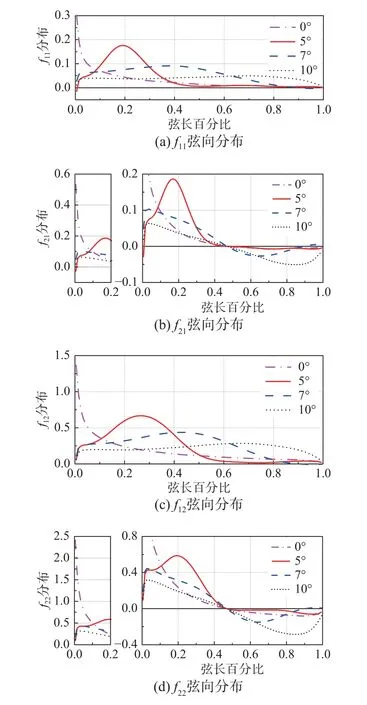
图26 90%展长截面广义力系数分布Fig. 26 Generalized force coefficients at 90% span section

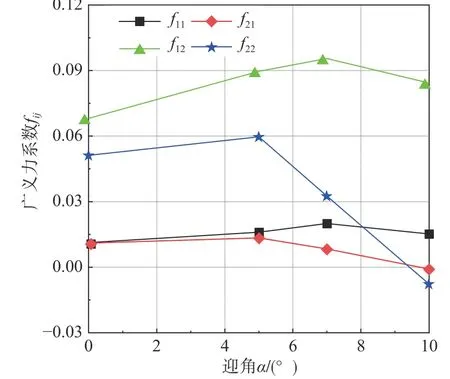
图27 通过式(14)积分得到90%展长截面的广义力系数Fig. 27 Generalized force coefficients at 90% span section is obtained by integrating equation (14)

5 结论

本文发展了流固耦合方法和ROM 方法计算初始迎角对颤振边界的影响。针对AGARD445.6 硬机翼模型，计算不同迎角和速度下的气动弹性响应并总结出了颤振特性随迎角的变化规律；在10°迎角下研究了考虑速度输入和不考虑速度的非定常气动力ROM，并预测了10°迎角的颤振特性；建立了考虑初始迎角输入的非定常气动力ROM 并预测了0°～10°不同迎角的颤振特性，最后分析了颤振边界随迎角变化的机理。本文主要结论如下：

(1)对于本文的AGARD445.6 硬机翼，当初始迎角小于5°时，随着迎角的增大，广义力系数幅值略微增加，导致颤振边界逐渐下降；初始迎角7°～10°，随着迎角的增大，展向涡的产生改变了机翼上翼面压强分布，导致二阶广义力系数的幅值下降，最终导致颤振边界的增加。

(2)基于RBFNN 的非定常气动力ROM 可以准确预测不同速度、减缩频率的非定常气动力，预测10°迎角的颤振边界时，考虑速度输入后ROM 的预测结果更精确，另外颤振预测的时域RK 法和频域VG 法预测结果基本一致。

(3)不考虑速度输入而考虑迎角输入的ROM能正确预测的颤振边界随迎角变化的趋势，与流固耦合计算不同迎角的颤振特性规律基本一致。