两边连接竖放波折钢板墙内嵌墙板抗侧性能及优化设计

2022-11-30谢志栋

工程力学 2022年12期

窦超，谢志栋，杨娜

(1. 北京交通大学土木建筑工程学院，北京 100044；2. 结构风工程与城市风环境北京市重点实验室，北京 100044)

钢板剪力墙结构体系符合双重抗震防线、延性好、耗能能力强等抗震设计要求，应用到许多高层及超高层建筑中，且近些年来出现了各种新的改进形式[1−4]。对于四边连接平钢板剪力墙结构国内外学者进行了大量的试验和理论分析[5−10]，形成了较为成熟的计算理论和设计方法。但研究同时发现，由于内嵌平钢板极易屈曲，形成的拉力带对框架柱产生较大的附加弯矩作用。为了避免拉力带对边缘框架的不利影响及门窗开洞的需要，XUE 和LU[8]提出了两边连接平钢板剪力墙，即内嵌墙板仅与框架梁相连、不与框架柱连接。虽然此类墙板改善了框架柱的受力，但由于缺少边缘构件的约束，墙板拉力带不能充分发展，其刚度和承载力受到较大削弱。

相比平钢板剪力墙，波折钢板墙中波折大大提高了墙板的面外刚度和抗剪屈曲荷载。合理设计时具有受剪屈服的抗侧机理，对边缘框架的锚固刚度要求以及附加弯矩的不利影响显著降低，同时滞回曲线饱满，耗能能力有显著提高[11−18]。对于四边连接波折钢板剪力墙已有很多学者开展了研究。EMAMI 等[11− 12]进行了波折钢板墙滞回试验及数值对比分析。结果表明，尽管发生剪切屈曲后墙板承载力会突然下降，但随即又逐步上升，并没有持续丧失承载力。KALALI 等[13]研究了波形钢板墙的单向推覆性能及滞回性能，指出合理选择波形钢板墙的板厚及波折尺寸时，能够获得比平钢板墙更优越的受力性能。ZHAO 等[14]的数值参数化分析发现，相比平钢板墙，波形钢板墙具有更好的抗震性能，并对周边框架的需求降低。DOU 等[16]提出了波折墙板的抗侧承载力公式，指出部分墙板存在屈曲或屈服后抗侧承载力显著下降的问题，延性是波折墙板设计中的一个重要指标。TONG 等[17− 18]对加劲波折钢板墙以及双层波折内嵌墙板的抗剪承载力进行了数值分析研究，提出了达到充分加劲效果的加劲构件刚度取值和极限承载力计算方法。FENG 等[19]通过理论推导得到了板带加劲波折墙板的屈曲荷载。ROUDSARI 等[20]通过数值分析研究了墙板开洞对波形钢板剪力墙的刚度、承载力和延性的影响。王威等[21]通过对4 片波形钢板墙及其与混凝土板组合墙体的低周往复加载试验并结合有限元研究，揭示了竖放波形钢板应用于组合墙体中可以提高其承载性能。DENG 等[22]提出了波形钢板剪力墙多高层整体结构的一种高效数值计算模型，可用来进行地震模拟分析。BROUJERDIAN 等[23]提出了一种平钢板和波折钢板通过螺栓连接形成的组合截面钢板墙，并对其抗侧性能进行了参数化数值分析。

由于波折墙板可看作正交异性板，其两个方向的面外抗弯刚度存在巨大差异，这就导致对于竖放波折墙板两侧边柱的约束对其性能影响很小，而上下框架梁的约束作用更大。利用这一特点，竖向放置的波折墙板更适合用于两边连接剪力墙中[24−28]。目前对于两边连接波折钢板墙以及加劲钢板墙，魏瑶等[24]讨论了加劲三角形波折墙板的弹性屈曲性能；赵秋红等[25]对竖放波折钢板墙的抗侧性能开展研究，指出受自由边影响其承载力下降约16%。FANG 等[26]对半刚性框架—两边连接竖放波折墙板开展了试验研究，并提出了屈服荷载及极限承载力的计算公式，但并未讨论墙板的选型及延性设计。

可以看到，已有研究主要集中在四边连接波折钢板剪力墙，而两边连接波折钢板墙的研究较少。一方面，大多数研究仅关注波折墙板最大抗侧承载力，而忽视了墙板屈曲后的承载力和延性性能[11−14]，但屈曲后性能对抗震设计又是尤为重要；另一方面，相比平钢板墙，波折钢板墙的几何参数更多、抗侧机理更为复杂，目前研究只是给出了墙板参数对抗侧或滞回性能的影响规律，至于这些关键参数在设计中如何取值，并未给出定量的明确的建议[17−18]。因此，设计人员在波折钢板剪力墙的初步设计时，如何进行内嵌波折墙板的选型即定量地选取墙板的各个几何参数，尚没有研究成果可供借鉴。在这种情况下，其不得不借助复杂的有限元软件来建模进行不断分析尝试，才能确定合理的墙板选型，这无疑为初步设计带来了巨大的困难，制约着波折钢板墙的推广应用。

针对上述问题，本文在对有限元分析模型进行充分验证的基础上，对两边连接竖放波折墙板的抗侧性能及优化选型进行数值分析研究，揭示墙板的抗侧机制及关键几何参数对抗侧性能的影响；在墙板两侧边设置加劲构件，提出侧边加劲构件的选型和刚度设计建议；最后，阐明了波折墙板在往复荷载下和单向推覆下的抗侧性能差异，并在往复荷载作用下提出了两边连接加劲竖放波折墙板的优化选型取值表，为墙板的初步设计提供了重要参考。

1 有限元模型及验证

由于本文研究目的在于重点考察内嵌墙板的抗侧性能(而不考虑框架作用)，因此如图1 所示采用单层单跨铰接刚性框架—波折墙板的分析模型进行单向推覆和往复加载分析。内嵌波折墙板竖向放置，仅与框架梁刚性相连。之所以采用无限刚性的梁柱铰接框架，是为了保证内嵌墙板单独承担水平剪力，不考虑框架的抗侧贡献。

图1 铰接刚性框架模型Fig. 1 Hinged rigid frame model

在有限元软件ABAQUS 中建立上述模型，所有构件均采用S4R 壳单元进行模拟。波折墙板采用双折线弹塑性模型的Q235 钢材，屈服强度fy=235 MPa，弹性模量E=206 GPa，切线模量Et=0.01E，泊松比ν=0.3。采用von Mises 屈服准则和随动强化理论，以考虑包辛格效应的影响。边缘框架的弹性模量取为100E来实现刚性框架。约束框架底梁全部自由度，通过耦合梁柱连接节点的平动位移实现铰接框架。在上梁端部加载点采用位移控制方式进行加载。考虑楼板对框架梁的面外约束，限制梁翼缘的面外侧移。采用静力隐式算法进行单向推覆和往复加载分析。采用一致缺陷法施加墙板的初始几何缺陷，即缺陷与第一阶屈曲模态一致，幅值为1/750H。为了准确描述波折墙板的受力和变形，每一个波折子板面沿波长方向划分4 个单元[27]，同时单元宽高比小于1.5。

为了证明本文采用的有限元数值模型及分析方法能够有效地进行波折钢板墙结构的抗侧性能分析计算，必须将其与现有试验结果进行对比。这里分别选取文献[11]和文献[15]的四边连接波折钢板墙往复加载试验进行模拟对比分析。对于文献[11]中的试件3，根据试验实际尺寸、材性实验参数及边界条件建立模型(图2(a))，其中，墙板高为H=1500 mm，宽为B=2000 mm，厚度为t=1.5 mm。图2(b)给出了有限元分析结果与试验结果的对比。有限元得到滞回曲线包络面积比试验稍大，总体能够获得与试验吻合的极限承载力。

图2 有限元与文献[11]的试验结果对比Fig. 2 Comparison of FEA and test results in Ref. [11]

文献[15]对单跨两层波折钢板墙进行了往复加载试验。选取试件HCoSPSW-Ⅰ进行建模分析，内嵌墙板尺寸为H×B×t=1100 mm×1100 mm×2 mm，有限元模拟结果与试验结果的对比如图3所示。可以看到，当层间位移角1.0%时，极限承载力的有限元结果为618 kN，试验结果为610 kN；达到最大层间位移角时，二者分别为538 kN 和514 kN。对比结果表明，有限元数值分析不仅能够准确地得到钢板墙的极限承载力，且能获得较为真实的强度退化规律即屈曲后性能。

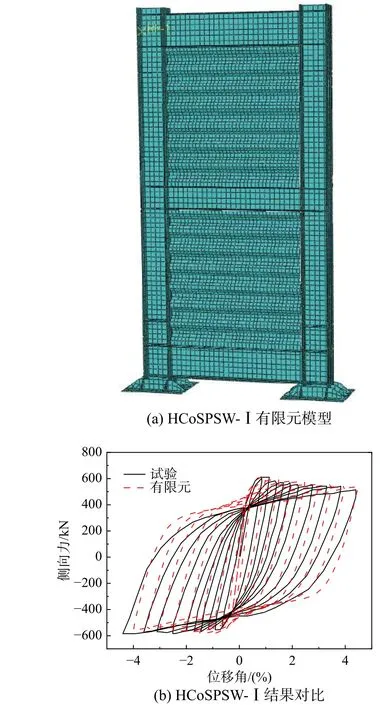
图3 有限元与文献[15]的试验结果对比Fig. 3 Comparison of FEA and test results in Ref. [15]

此外，对于两边连接竖放波折钢板墙，文献[28]开展了滞回性能试验研究。如图4(a)所示，试件S-3的开洞率为33%，墙板尺寸为H×B×t=1000 mm×1200 mm×3 mm，左右两侧边设置有100 mm×10 mm的平板加劲肋条。同理，采用文献[28]中的相同尺寸及材料、边界参数建立有限元模型(图4(a))进行往复加载分析，滞回曲线如图4(b)所示，与试验结果吻合较好，极限承载力比试验值低约4.6%，最大层间角时的承载力比试验值高约7.0%。

图4 有限元与文献[28]的试验结果对比Fig. 4 Comparison of FEA and test results in Ref. [28]

综上，本文采用ABAQUS 对波折钢板墙的建模和分析方法具有可行性，分析结果可靠，可以基于数值结果提出相应设计方法和建议。

为了更加直接地比较不同参数对内嵌波折墙板的影响，将墙板承载力进行归一化。定义内嵌墙板的最大承载力为极限承载力Vs，与大震层间位移角限值2.0%所对应的承载力称为残余承载力Vr，对应的归一化极限承载力系数φs和残余承载力系数φr分别为：

2 竖放波折墙板的抗侧曲线

Vy为墙板全截面剪切屈服承载力：

式中：τy为钢材剪切屈服强度；B和t分别为墙板的宽度和厚度(图1)。

上述两个承载力系数直接反映了墙板的承载效率，其越接近1.0 表明墙板以抗剪屈服机制为主，越接近面内抗剪受力状态，材料利用率越高。此外，残余承载力系数与极限承载力系数的比值φr/φs可用来评估墙板屈曲后承载性能，其值越大表明屈曲后承载力越稳定。

波折内嵌墙板的几何参数不同，其抗侧承载力曲线将会有显著差异，主要反映在屈曲后承载力及延性性能。选取两个典型算例，其几何参数及抗侧曲线如图5 所示。相比于第一类较为稳定的抗侧承载力，第二类曲线在极值点后出现迅速下降，表现出极不稳定的屈曲后承载能力，导致墙板的延性性能较差。因此在设计中，应通过波折墙板的优化选型，避免第二类情况出现。

图5 典型波折钢板的荷载-位移曲线Fig. 5 Load-displacement curves of typical corrugated steel plates

定义对应于上述两类曲线的墙板分别为“强墙板”和“弱墙板”，具体量化指标为：弱墙板残余承载力系数与极限承载力系数的比值φr/φs<0.85，意味着屈曲后承载力下降明显；而强墙板的φr/φs≥0.85，也就是说到达最大层间位移角时仍保持足够延性。

图6 所示为强墙板(算例1)和弱墙板(算例2)在最大层间位移角下的等效应力图，阴影区域代表材料屈服。可以看到，强墙板的屈服面积明显要比弱墙板的屈服面积大。强墙板能够实现平面内受剪从而接近于全截面屈服，而弱墙板部分截面并没有达到屈服。

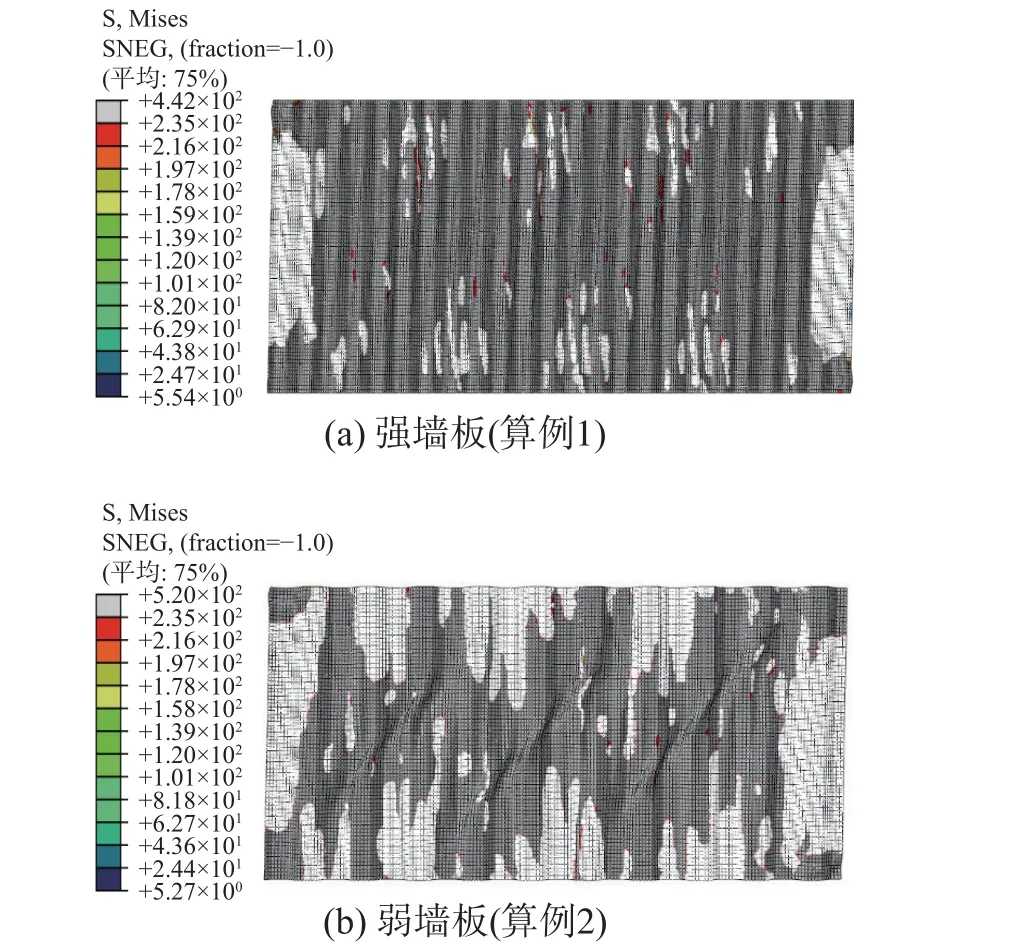
图6 典型波折钢板的等效应力图(层间位移角2%)Fig. 6 Equivalent stress diagram of typical corrugated steel plate (drift ratio 2%)

强墙板和弱墙板在残余状态下的面外变形模式不同(图7)，强墙板的面外变形为横跨几个波折的整体变形，最大面外变形为70 mm；而弱墙板的面外变形为横跨几个波折的“拉力带”变形，最大面外变形为93 mm。墙板面外变形的不同，导致墙板的抗侧机制发生不同。

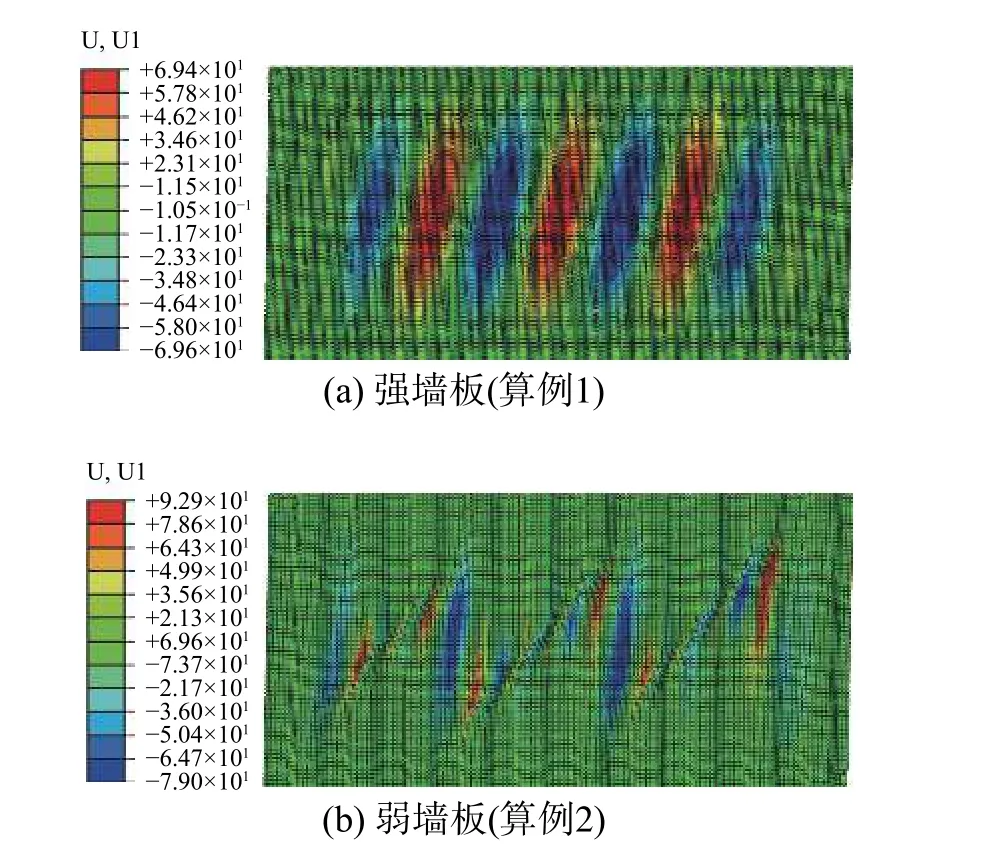
图7 典型波折钢板的面外变形(层间位移角2%)Fig. 7 Out-of-plane deformation of typical corrugated steel plate (drift ratio 2%)

3 几何参数对墙板抗侧性能影响

两边连接竖放波折墙板在设计时，需要6 个几何参数才能确定其外形特征(图1)，进而决定其抗侧性能，即墙板高度H、宽度B、墙板厚度t、波长Cl、波高Ca和波折角度θ。相比平钢板墙只有H、B和t的情况，波折墙板的几何选型复杂的多。

如前所述，上下框架梁的约束对竖放波折墙板影响很大。随着层高的增加，框架梁的约束作用减小，导致墙板的面外变形增大、面内剪切抗侧效率降低。图8 给出了不同高度下墙板的抗侧曲线，随着墙板高度增大其初始刚度及承载力均有所下降，尤其屈曲后抗侧曲线更为明显。

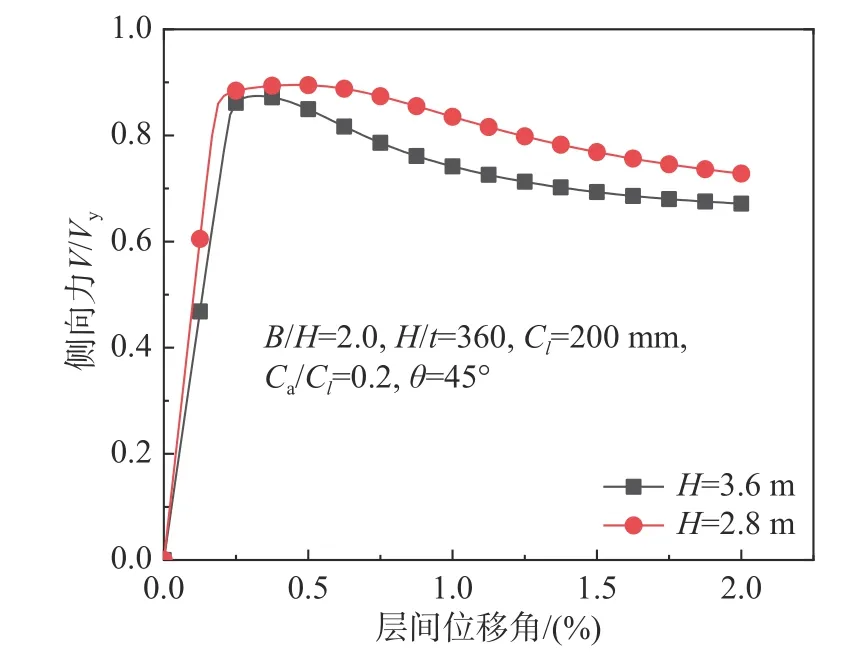
图8 墙板高度对抗侧承载力的影响Fig. 8 Effect of wall panel height on lateral resistance

因此，根据相关国家规范[29−31]，为了满足墙板选型的适用性，后续分析中波折墙板高度均偏于保守地取为H=3.6 m，采用Q235 钢，屈服强度fy=235 MPa。对于其他墙板参数的选取，结合前人研究，涵盖工程常用范围：B/H=0.5～2.0，H/t=240～900，Cl=300～700 mm，Ca/Cl=0.10～0.20，θ=30°～90°。

3.1 波折角度

保持其他参数不变，变化波折角度进行推覆分析，典型算例结果如图9 所示。随着波折角度θ 的增加，墙板的抗侧承载力尤其是屈曲后承载性能明显提升。这是因为，增大波折角度竖放墙板绕强轴的弯曲刚度将会增大[17]，从而减小波折板的面外变形，改善其面内抗侧受力。因此，在墙板选型设计中，在条件允许时建议选择较大的波折角度。其他算例得到类似结论，在此不赘述。

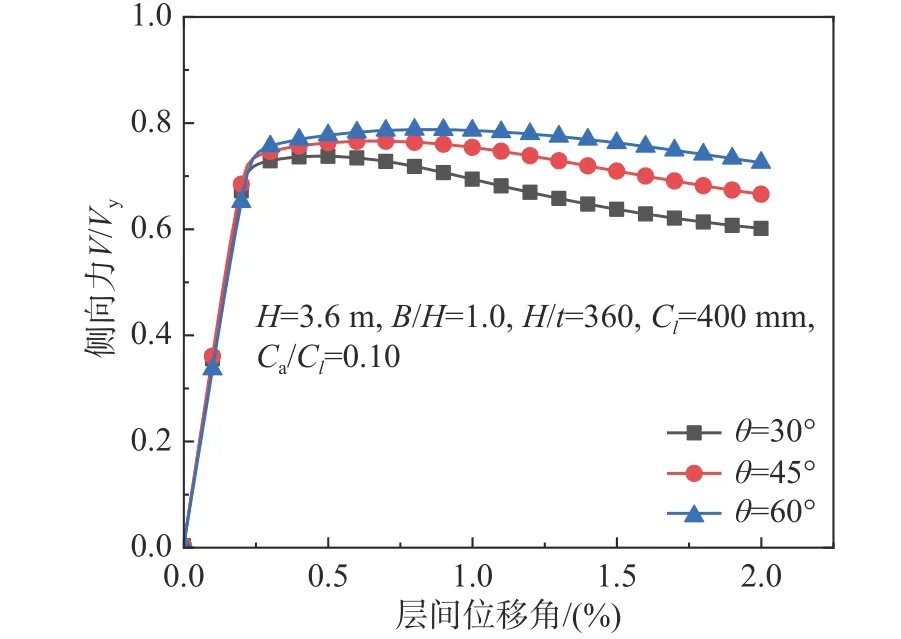
图9 子板面波折角度对抗侧承载力的影响Fig. 9 Effect of sub-panel inclined angle on shear resistance

3.2 墙板宽高比

选取算例：①H=3.6 m，H/t=600，Cl=500 mm，Ca/Cl=0.10，θ=45°；②H=3.6 m，H/t=450，Cl=600 mm，Ca/Cl=0.10，θ=45°；③H=3.6 m，H/t=360，Cl=400 mm，Ca/Cl=0.20，θ=45°，变化墙板宽高比B/H=0.5～2.0进行单向推覆分析，提取极限承载力和残余承载力如图10 所示。同时，图11 给出了算例3 中B/H=1.0时墙板残余承载力对应的主应力状态。

图10 宽高比对墙板承载力系数的影响Fig. 10 Effect of aspect ratio on strength coefficient

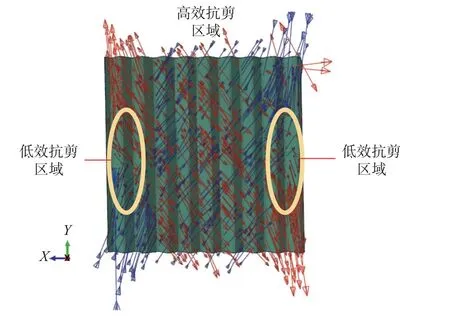
图11 墙板主应力(层间位移角2.0%时)Fig. 11 Principal stress distribution (drift ratio 2%)

可以看到，同一组算例随着宽高比的增加，墙板承载力系数增大，这表明抗侧效率提高，但增长速度逐渐变缓。这是由于墙板两侧边无有效约束，附近存在“低效抗剪区”(图11)，使部分墙板不能有效参与抗侧；而宽高比越大即墙板越宽，自由边的低效抗剪区所占墙板总面积的比例越小，对承载力影响也相应减小。

图12 为算例3 中不同宽高比下残余承载力状态即最大层间位移角时墙板屈服情况(阴影区表示屈服，非阴影区表示未进入屈服)。当宽高比较小时(B/H=0.5)，无约束自由侧边的影响很大，墙板大部分区域没有有效参与抗剪进入屈服，导致承载力系数较小。当宽高比增大到2.0 时，未进入屈服的低效抗剪区占比很小，墙板表现出较高的极限承载力系数和残余承载力系数，抗侧性能接近四边连接墙板。

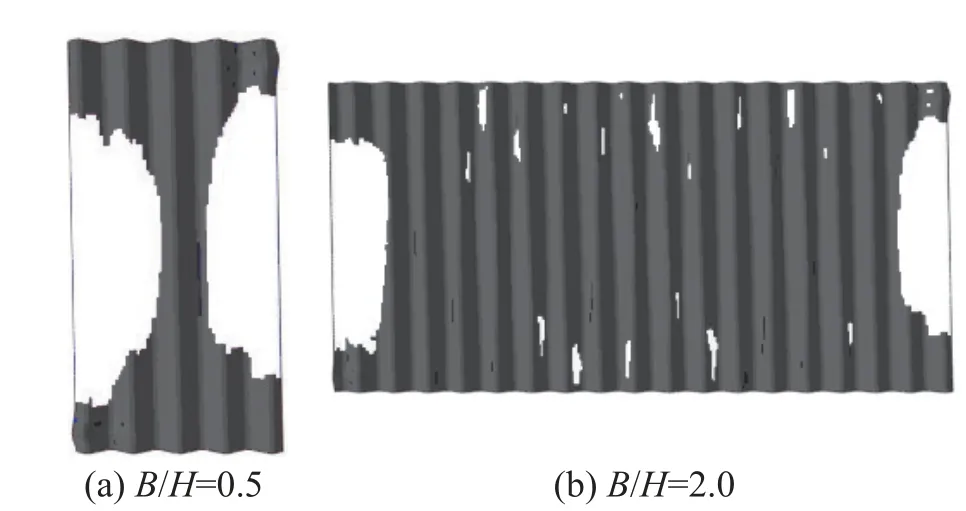
图12 宽高比对墙板屈服面积的影响Fig. 12 Effect of aspect ratio on yield area of wall

3.3 波形比

波形比Ca/Cl是波折墙板区别于平钢板的最大特征。典型算例的单向推覆抗侧曲线随波形比的变化如图13 所示。当波形比过小时(<0.10)，墙板的屈曲后承载力下降较快，残余承载力较低，延性较差。

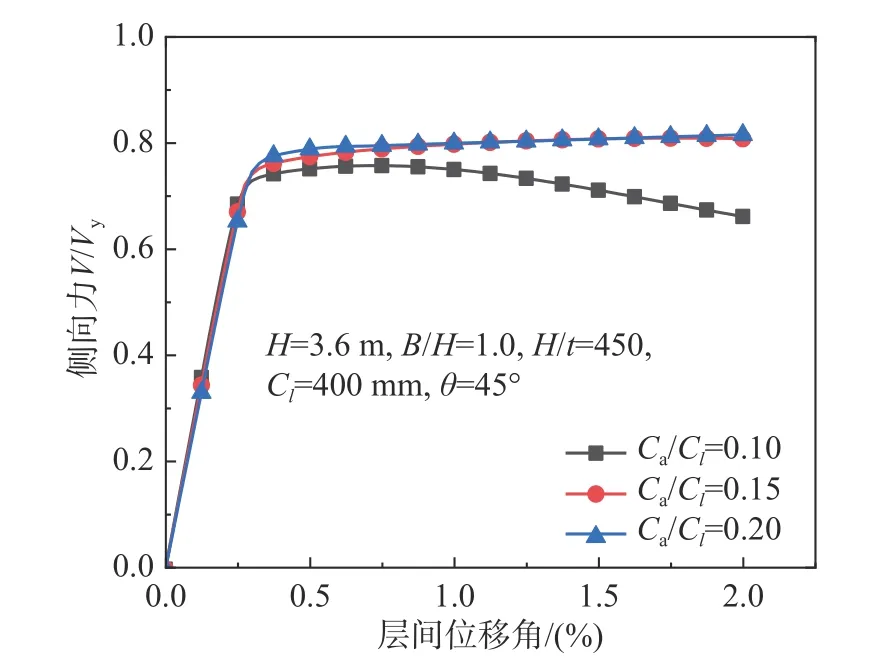
图13 波形比Ca/Cl 对承载力的影响Fig. 13 Effect of corrugation ratio on lateral resistance Ca/Cl

如图14 所示，不同波形比下墙板的面外变形模式相似，但Ca/Cl=0.10 时最大变形为112 mm，而Ca/Cl=0.15 时，墙板面外刚度显著增大，面外变形减小至仅为54 mm。墙板面外变形过大，使得墙板不再处于完全的面内纯剪状态，其承载力随着面外变形的增大而下降。其他算例下的结果类似，在此不赘述。研究分析表明[27]，过大波形比可能引起波折墙板发生相关屈曲破坏而导致承载力下降，因此在初步设计时，建议Ca/Cl在0.10～0.20 范围内取值。

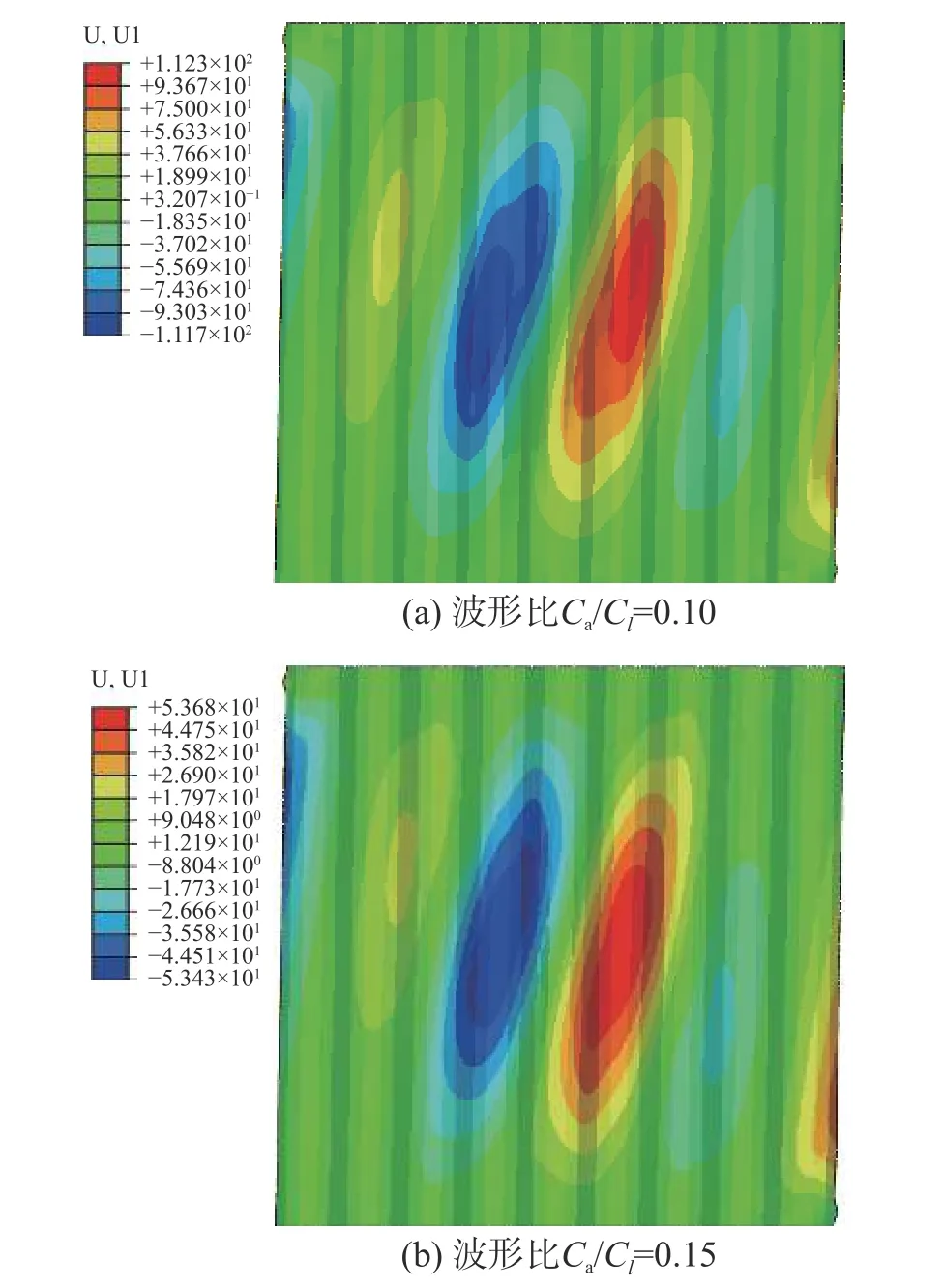
图14 不同波形比墙板的面外变形(层间位移角2%)Fig. 14 Out-of-plane deformation of panels with different corrugation ratios (drift ratio 2%)

3.4 高厚比与波长

如图15 所示，随着墙板高厚比H/t的减小(厚度增大)，其面外刚度增大面外变形减小，更接近面内抗剪受力状态，因此，承载力尤其是屈曲后承载力提高且更加稳定。

图15 高厚比对承载力的影响Fig. 15 Effect of height-to-thickness ratio on lateral resistance

墙板的波折长度Cl也是一个重要参数。图16的算例结果表明，波折长度对屈曲后承载性能及残余承载力系数影响较大。此外，随波折长度的增加，墙板残余承载力系数先增大后减小，也就是说存在最优波长，使得墙板的抗侧性能最优。

图16 波长对承载性能的影响Fig. 16 Effect of corrugation length on lateral resistance

从图17 和图18 可以看到，当波长Cl=400 mm时，墙板在残余状态下发生整体面外变形，但变形量较小，因此大部分区域的主应力为45°方向，即处于纯剪状态；当波长增大到700 mm 时，发生类似“拉力带”的局部变形，主应力方向改变，墙板不再是面内纯剪状态，导致抗侧曲线的下降。

图17 不同波长墙板的面外变形(层间位移角2%)Fig. 17 Deformation of corrugated panels with different corrugation length (drift ratio 2%)

图18 不同波长墙板的主应力(层间位移角2%)Fig. 18 Principal stress distribution of wall panels with different wavelengths (drift ratio 2%)

正是由于波长变化引起墙板面外变形破坏模式的改变，进而影响了墙板的抗侧稳定性能，导致最优波长的存在。为了得到最优长细比Cl*，进行大量变参数分析，发现最优长细比Cl*与其他几何尺寸之间存在如下关系：

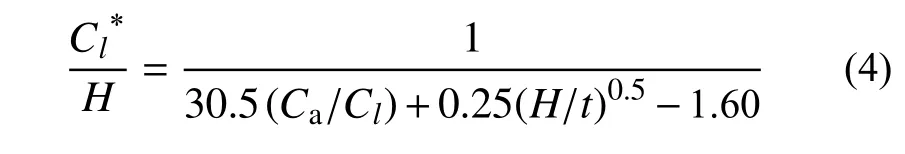
拟合式(4)与有限元结果对比如图19 所示。以图16 中的算例为例，由式(4)可得最优波长Cl*≈390 mm，与有限元结果Cl=400 mm 接近。

图19 最优波长结果Fig. 19 Result of optimal corrugation length

综上，在进行墙板的选型设计时，宽高比宜B/H≥1.0，波形比宜Ca/Cl≥0.15，波折角度宜θ≥45°，并根据式(4)确定最优波长Cl*，以使墙板具有较高的极限承载力、残余承载力及足够的延性性能。

4 两边加劲竖放波折墙板

由3.2 节可知，两边连接波折墙板的两自由边存在低效抗剪区。为了提高墙板的抗侧效率，本节对竖放波折墙板两侧自由边设置加劲构件，对加劲效果进行分析，提出加劲构件的设计建议。

4.1 加劲构件形式

两边连接竖放波折墙板中，两侧加劲构件提供了约束作用限制板边的面外变形，因此，加劲构件可不与框架梁连接，此时，暂不考虑加劲构件平面内抗弯刚度的影响。选用两种形式的加劲构件，单块钢板和方钢管(图20)，分别对典型算例设置两种加劲构件，抗侧性能如图21 所示。每组算例中，两种加劲构件的面外抗弯刚度相同，但方钢管的扭转刚度要显著大于加劲平钢板。

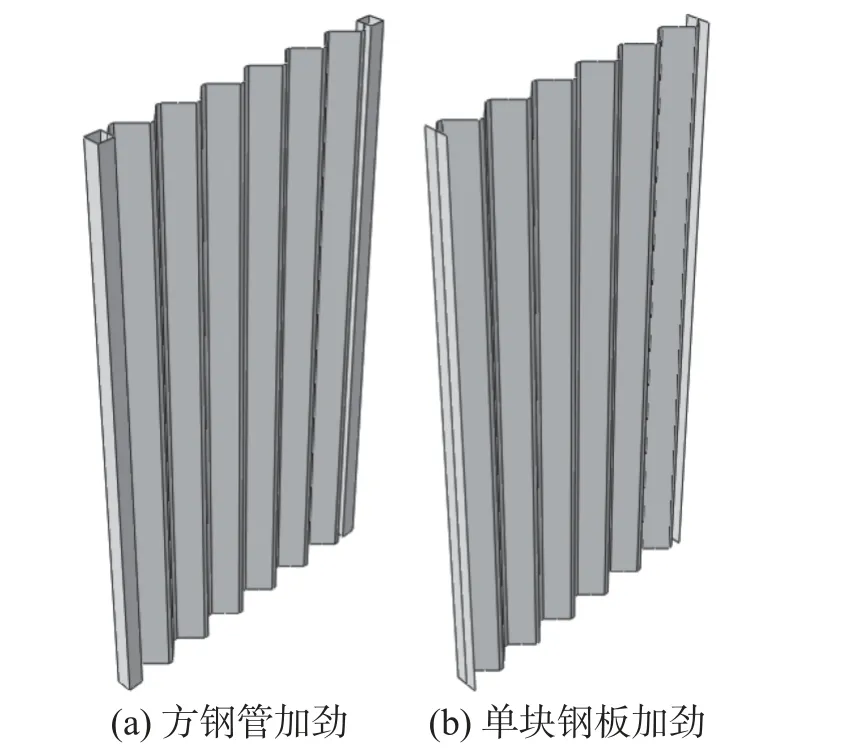
图20 加劲构件的形式Fig. 20 Form of stiffening member

图21 墙板加劲构件对抗侧性能的影响Fig. 21 Effect of stiffeners on the lateral resistance

结果表明，边缘加劲构件可显著提升竖放波折墙板的极限承载力和残余承载力。对于大宽高比墙板(B/H=1.5)，加劲构件的扭转刚度则对加劲效果几乎没有影响，主要是其面外抗弯刚度的贡献；对于小宽高比墙板(B/H=0.5)，扭转刚度有一定影响，但相比面外刚度仍然较小。

此外选取图22 的两个算例，加劲构件的面外抗弯相同但面内抗弯刚度不同，且加劲构件与框架梁相连。可以看到，加劲构件的面内刚度对墙板的抗侧性能几乎没有影响。其他算例得到类似结论，在此不赘述。

图22 加劲构件面内抗弯刚度对抗侧性能的影响Fig. 22 Effect of in-plane flexural stiffness of stiffening members on lateral resistance

综上，加劲构件的面外抗弯刚度对加劲效果起到决定性作用。在设计中，加劲构件建议选用方钢管，其截面开展、加劲效果更好。

4.2 界限约束刚度比

为了反映边缘加劲构件对墙板两侧边的约束强弱，引入约束刚度比η 参数，定义为加劲构件面外抗弯刚度与内嵌墙板抗弯刚度之比，即：

式中：Is为加劲构件的平面外抗弯惯性矩；Dx为墙板的强轴弯曲刚度；H为墙板的高度[17]。

选取典型墙板算例，变化加劲构件的刚度，得到墙板残余承载力系数如图23 所示。可以看到，当加劲构件的面外抗弯刚度较小时，墙板的残余承载力系数随着约束刚度比的增大而显著提高；随着约束刚度比的继续增大，残余承载力系数的增速减缓，这说明已起到了充分加劲作用。此外，对于不同宽高比的墙板，加劲构件的加劲效率也有所不同：宽高比较小时(B/H=0.5)，承载力提高程度更高，但达到充分加劲(即曲线接近走平)所需的约束刚度比也越大。

从上述算例结果可知，当约束刚度比η≥0.60 时，墙板的残余承载力系数已超过完全约束时的90%，此时可认为加劲构件为墙板两侧边提供了充分的支承和约束作用，对于其他墙板具有相同的结论，在此不再一一给出。

因此，本文将η*=0.60 定义为“界限约束刚度比”。当加劲构件采用界限约束刚度比时：一方面改善了墙板的抗侧性能；另一方面随着墙板的宽高比增大，加劲效果逐渐减弱(图23)。这也与前述分析结论一致：宽厚比越小的墙板其两侧自由边的影响越大，因而更需要进行加劲。图24 给出了算例1 中B/H=0.5 的墙板在未加劲和界限约束刚度加劲下，达到最大层间位移角时墙板的屈服区域。可以看到，加劲后墙板的低效抗剪区域明显减小，承载性能得到显著提升。

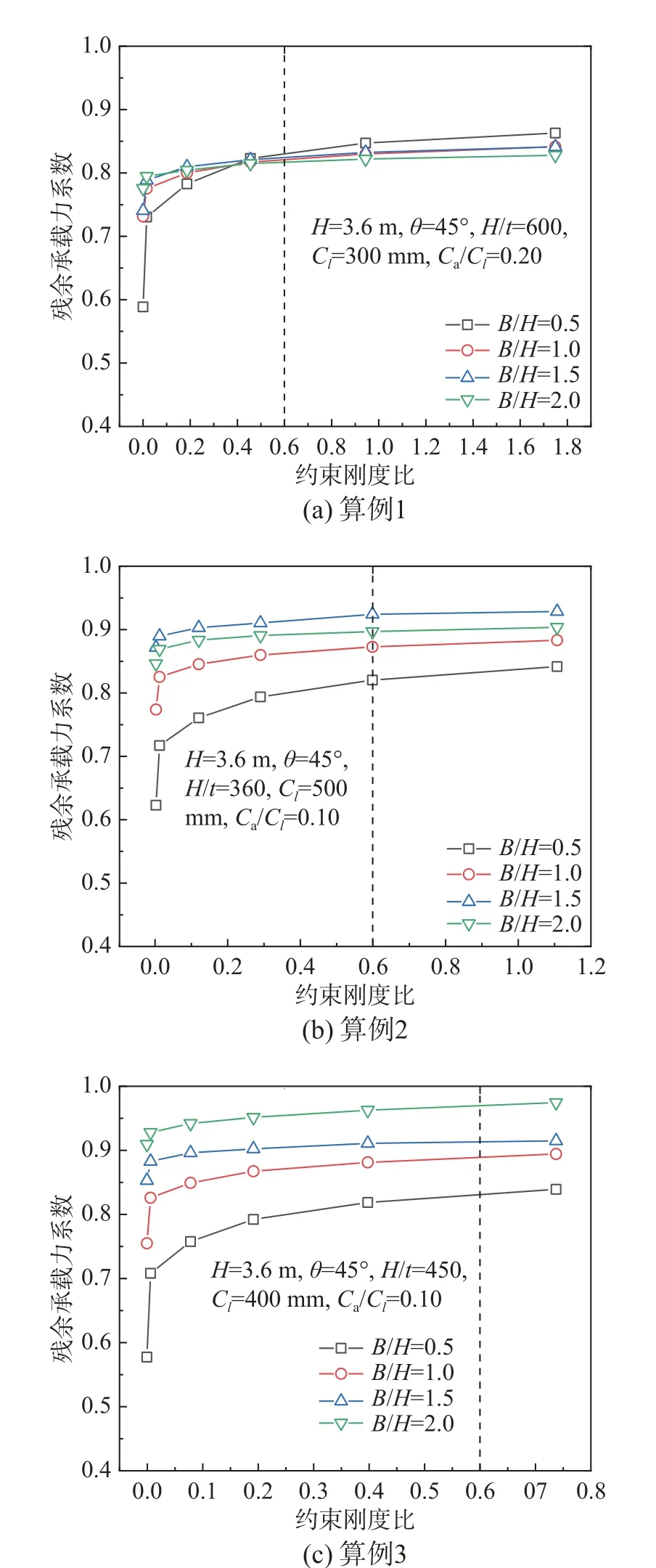
图23 加劲构件约束刚度比的影响Fig. 23 Effect of restraint stiffness ratio on lateral resistance

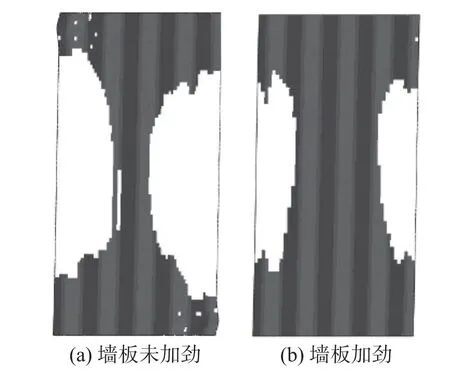
图24 墙板加劲前后屈服区域对比(层间位移角2%)Fig. 24 Yielding areas before and after stiffening for corrugated panels (drift ratio 2%)

5 往复加载下的抗侧性能及设计

波折钢板剪力墙的内嵌墙板作为抗侧构件，在地震作用下应当具有足够的变形和耗能能力，起到消能减震的作用。本节对两边连接加劲竖放波折墙板在往复荷载作用下的滞回性能进行分析。通过在上部梁端施加水平位移实现往复加载，按照层间位移角±0.5%、±1.0%、±1.5%、±2.0%的四个级别施加，每一级加载循环一次。

5.1 墙板的滞回曲线及骨架曲线

选取第2 小节单向推覆分析中弱墙板的典型算例：H=3.6 m，B/H=1.5，H/t=600，Cl=400 mm，Ca/Cl=0.10，θ=45°。图25(a)给出了墙板的滞回曲线，当层间位移角超过±0.5%后，峰值承载力随着位移角的增加而显著下降，表明墙板屈曲后抗侧性能极不稳定，影响了其延性和耗能能力。

图25(b)为墙板滞回分析的骨架曲线和单向推覆下抗侧曲线的对比。当层间位移角小于±1.0%时，骨架曲线与单向推覆曲线基本重合；但当层间位移角继续增大超过±1%后，骨架曲线呈现出明显的强度退化现象，最大层间位移角对应的残余承载力比单向推覆时降低了18%。究其原因，在于往复加载下面外残余变形在每个加载循环中不断的积累增大，导致加载后期墙板的变形将非常显著，大于单向推覆时同等层间位移角下的面外变形，因此承载力更低一些。

同样，对于单向推覆分析中的强墙板，选取典型算例：H=3.6 m，B/H=1.5，H/t=360，Cl=400 mm，Ca/Cl=0.20，θ=45°，分析结果如图26 所示。可以看到，墙板滞回曲线饱满呈梭形。并且随着层间位移角的增大，极限承载力逐渐上升，直至层间位移角2%时，这意味着强墙板具有稳定的承载力、足够的延性和良好的耗能能力。

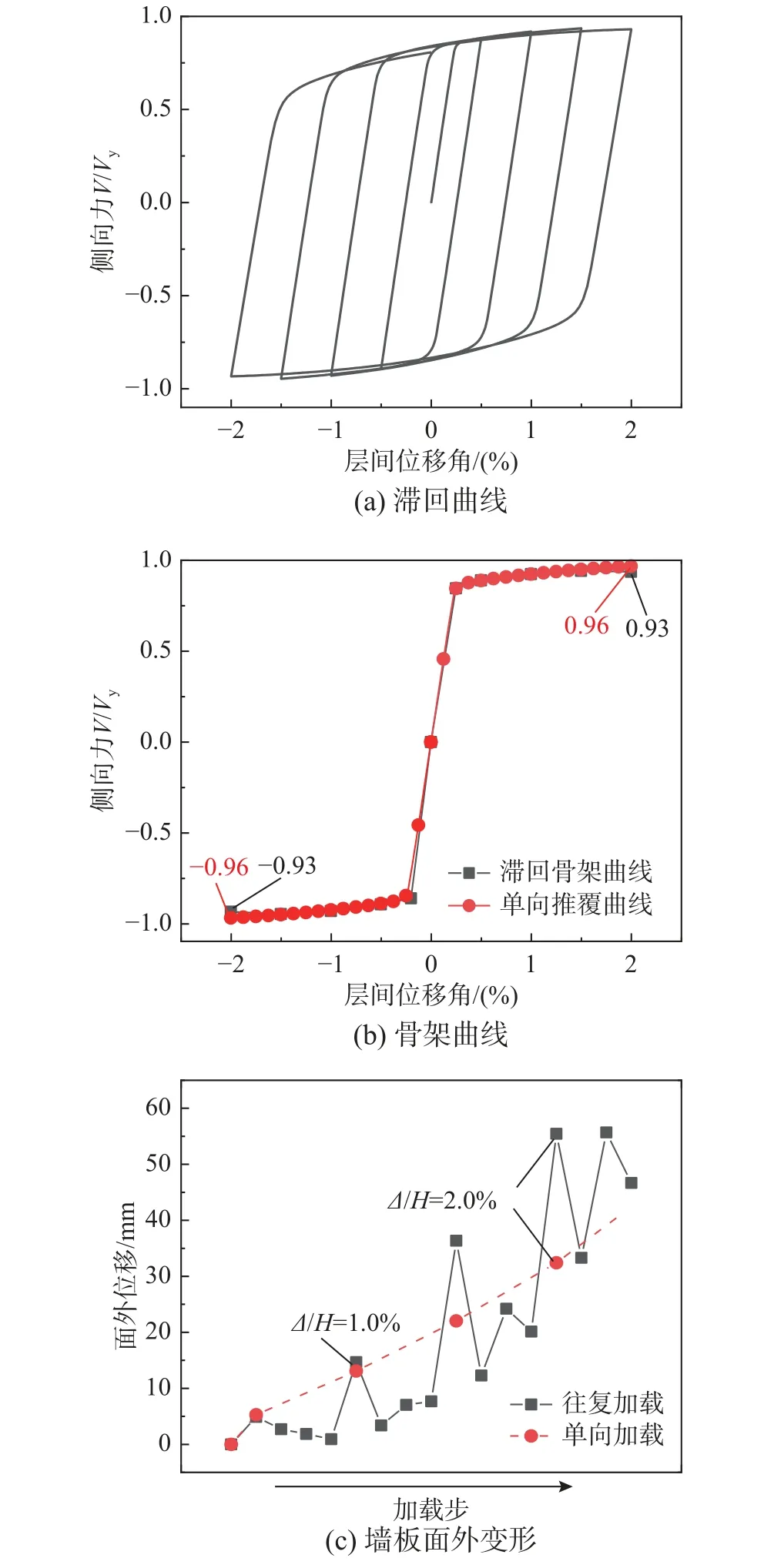
图26 单向推覆与滞回分析对比(强墙板)Fig. 26 Comparison of monotonic pushover and hysteresis analysis (strong wall panel)

图26(b)表明，与弱墙板不同，强墙板的滞回骨架曲线与单向推覆曲线基本重合。这是由于尽管往复加载下墙板面外变形仍不断积累，但此强墙板在层间位移角2%时最大面外变形只有55 mm，且与单向推覆下的面外变形量比较接近(图26(c))。

5.2 墙板优化设计建议

如前所述，对于内嵌波折墙板，其优越的抗侧及滞回性能的发挥依赖于墙板参数例如宽高比、高厚比、波折角度、波长和波形比等的合理取值，设计中应避免选择“弱墙板”。但由于影响参数众多，波折墙板的初步设计选型是一件复杂且困难的事情。因此，如何合理选择墙板参数，使其具有良好的抗侧承载力、延性变形及耗能能力，是设计人员急需的。

5.1 节分析表明，由于往复加载下墙板的面外累积变形，会导致滞回分析的骨架曲线通常低于单向推覆曲线。在抗震设计中，墙板的滞回性能相比单向推覆性能更为重要，因此，本节基于往复加载分析，提出两边连接加劲竖放波折墙板的优化选型建议。选定墙板性能的优化目标为：在往复加载下达到最大层架位移角2.0%时的残余承载力系数φr≥0.85，同时φr/φs≥0.85，后者保证了墙板在最大层间位移角时仍有足够的承载力，即骨架曲线没有明显的强度退化，具备良好的延性变形和耗能能力。此外，优化分析模型中加劲构件与框架梁刚接，其约束作用更大。

在第3 节的墙板参数取值范围内进行大量变参数分析，共128 个算例，从中选择满足上述优化目标的参数组合，最终确定墙板优化选型如表1所示。本表适用于钢材等级等于或低于Q345、同时采用方钢管加劲构件且满足界限肋板刚度比η*≥0.60 的情况。可以看到，采用优化选型的墙板后，在墙板层间位移角2%时依具有足够的抗侧能力(φr≥0.85)。设计人员设计波折墙板时，可根据水平荷载首先确定墙板的宽度和厚度，再基于表1根据宽高比和高厚比确定其他参数使得墙板的抗侧性能达到最优。

设计两个优化墙板，对表1 的适用性进行验证：①H=3.2 m，B/H=0.5，t=8 mm，Cl=400 mm，Ca/Cl=0.15，θ=60°；②H=3.0 m，B/H=1.0，t=12 mm，Cl=500 mm，Ca/Cl=0.1，θ=75°，滞回曲线如图27所示。可见，根据优化选型表进行初步设计得到的墙板其滞回曲线饱满，承载力稳定，具有很好的延性和耗能能力。