双余度机电作动系统静态力均衡技术研究

杨建忠，石林轩，孙晓哲

(1.中国民航大学安全科学与工程学院，天津 300300；2.中国民航大学天津市民用航空器适航与维修重点实验室，天津 300300)

0 前言

随着电传飞控技术的发展，多电/全电飞机已成为未来民机的发展方向与趋势，其中，大量采用电力作动技术是多电飞机最重要的特征之一[1]。现在的功率电传作动器主要有电静液作动器EHA(Electro-Hydrostatic Actuator)和机电作动器EMA(Electro-Mechanical Actuator)，其中EMA直接采用电力驱动，完全消除了对液压的依赖。虽然现阶段由于机械卡阻等问题导致其不能大量应用到主飞行控制舵面上，但是它仍然是未来飞机实现多电/全电的关键应用[2]。波音787将EMA用在了扰流板和水平安定面[3]。C919的水平安定面也使用了EMA。

作动系统是飞行控制系统中关键的子系统，它必须要有很高的安全性和可靠性。根据适航规章25.1309要求，要保证其高安全性概率要求，一般采用余度技术，由于主动/主动的工作模式与主动/被动工作模式相比具有输出力大、故障瞬态小、对故障检测要求低等优点，被普遍认为是该系统应用在飞机上的优选形式[4]。目前，机电作动系统的架构布局以及工作驱动形式被广泛研究和讨论，包括欧盟和美国波音。1999年，由欧洲国家资助的HISYS项目中提出的一种双余度的机电作动系统，2个余度之间完全独立，没有机械交联，实现了最高的灵活性，该系统作为原型，在空客的集成测试台进行了测试[5]。在波音的COVADIS项目中，以A320为原型开发了用在副翼上的机电作动器，它也是一种双余度的架构布局，该系统进行了铁鸟实验以及飞行实验[6]。

然而，要使这种余度主/主式EMAs能大量应用到飞行控制系统甚至是主控舵面上，需要解决的关键问题之一是力纷争问题。由于并联驱动舵面的各个通道的差异导致了作动器之间输出位移和力不一致，引起同一舵面多个主动作动器之间互为负载和相互对顶的现象即为“力纷争”现象。力纷争现象长时间存在会使舵面结构疲劳甚至破坏，严重时影响飞行安全[4]。现在已经有大量关于余度液压作动器以及液压与功率电传作动器的混合作动器的力纷争研究并且取得了较为理想的成果，文献[4，7-8]对传统的余度作动系统的力纷争研究提出了很多可以参考的均衡方案。WANG和MARÉ[9]在2014年提出了通过在位置控制回路中引入均衡偏移量，它是作为作动器之间的力差值的积分函数来实现静态力均衡的。COCHOY等[10]提出了2种通过引入位移、速度以及力等差值反馈的控制策略，力纷争现象得到了很好的改善。付永领等[11]在2014年提出了3种减小静态力纷争的力均衡控制策略，这些方法对力纷争都有不同程度减弱效果。

现阶段文献研究对于余度EMAs的力纷争研究甚少，因其力纷争形成原因和机制的特殊性，在一定条件下会对系统造成较大影响，因此必须采取有效的方法将它消除或限制[12]。

德国宇航中心(DLR)在2017年研究总结了双余度主/主式机电作动器系统的力纷争形成的关键原因，仿真得出了这些原因能够带来的最严重的影响，总结出对该种系统采取力均衡控制的必要性。该机构在2018年研究了一种有效的力均衡控制方法，包括最优线性二次输出调节器(LQR)的反馈回路和基于一般回归神经网络(GRNN)的前馈控制器，所实现的控制方案在与商用单通道飞机副翼物理特性相匹配的实验平台上进行了验证[12-13]。但是这些研究没有特别区分到动、静态力纷争机制上的不同，对其设计的力均衡控制方法在理论上也没有针对性。

本文作者针对双余度机电作动系统的特点，深入探究其静态力纷争产生的根本原因，并据此提出相应的静态力均衡控制方案并仿真验证其效果。

1 双余度机电作动系统建模

1.1 EMA建模

所研究的EMA为齿轮驱动式，丝杠和电机单独安装，齿轮箱用于连接电机和螺母。忽略换相过程对无刷直流电机的影响，则基本方程[14]为

(1)

其中：Uc为控制电压；Rc为绕组电阻；Lc为绕组电感；Cm为电磁转矩系数；Ce为反电动势系数；TL为电机轴的负载转矩；i为电机电流；ω为电机角速度；Jm为电机侧转动惯量；Bm为阻尼系数；F为滚珠丝杠负载；ig为齿轮减速比；p为滚珠丝杠导程；x为作动器直线输出位移。

系统仿真参数如表1所示。系统的参数由物理襟翼机电作动系统缩比模型经过系统辨识得到。

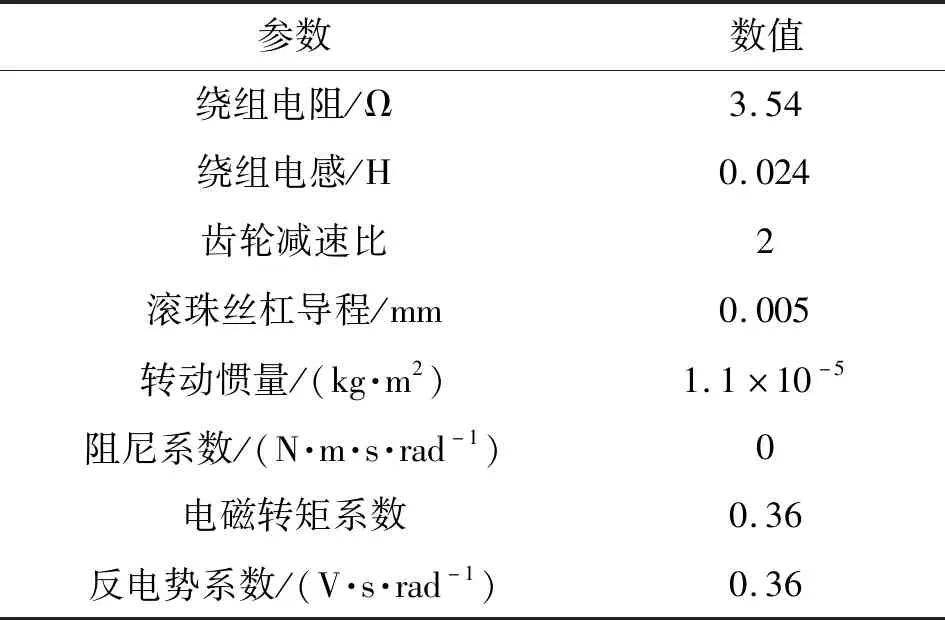
表1 系统仿真参数

根据系统参数和某商用飞机的系统性能要求设计了控制器[9]，性能主要包括动态跟随性能和抗负载性能。该系统采用三闭环控制，由外到内分别为位置环、转速环、电流环。对设计的控制器进行仿真和实验验证。

1.2 舵面建模

研究的双余度主/主式机电作动系统由2个相同的EMA并联驱动舵面共同承担负载，它与舵面的连接处用连接刚度来表示：

(2)

式中：kL1、kL2为连接刚度；x1、x2为输出位移；F1、F2为输出力；FL为舵面的外部空气负载；xt为舵面位移；mt为舵面质量。

综上，得到了考虑舵面气动负载和连接刚度的双余度机电作动系统的完整数学模型，如图1所示。

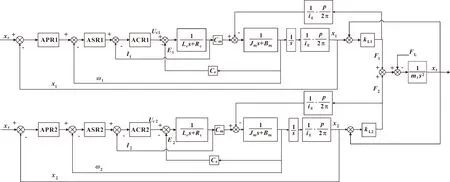
图1 EMAs完整模型方块图

2 静态力纷争分析

当系统接受指令并到达稳态后,通道的输出力持续不一致的现象就是静态力纷争;而动态力纷争就是系统到达稳态之前的瞬态过程中通道输出力不一致的现象。静态力纷争可以引起作动器之间长时间力不平衡的现象，严重时甚至会造成通道间不但没有共担负载，反而互为负载，从而可能会破坏系统结构，造成重大影响。动静态力纷争的定义如图2所示。

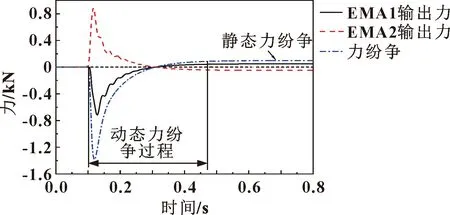
图2 动静态力纷争定义

通过数学推导分析使系统产生静态力纷争的主要因素，并进行仿真分析和验证，评估它们对力纷争的影响程度，为下一步设计静态力均衡控制方法提供理论依据和基础。

2.1 静态力纷争数学分析

通过传递函数的方框图等效，得到带三闭环控制的双余度机电作动器系统方块图如图3所示。

图3 双余度机电作动系统等效方块图

由图3可得:

(3)

(4)

由于系统输入的都是阶跃信号，因此当系统达到稳态时，各部分的直流增益为

G1(0)=G2(0)=1;H1(0)=H2(0)，代入式(3)，并由式(3)—(4)可得:

(5)

所以当系统达到稳态时，得

(6)

以上只是一个理想情况。在实际系统中，还存在一些例如位置传感器的反馈参数偏置、传动装置间隙等不确定性因素使得作动器输出位置产生静态偏差，这些因素也会引起系统产生一定程度的静态力纷争[11]。因此，2个通用的位置偏移E1和E2额外引入到公式中，它们可以用来代表所有因为系统不确定性因素导致的静态位置误差。式(6)经过改写后，得到静态力纷争等式为

(7)

其中：E1为通道1的不确定性所造成的位置误差；E2为通道2的不确定性所造成的位置误差。

由式(7)可知：各个EMA的输出力主要由2个因素决定的，分别是连接刚度不一致和不确定性因素造成的静态位置误差。

2.2 仿真分析与验证

下面将通过2个实例仿真来验证上述分析：

(1)为了不让控制器进入饱和的非线性工作状态，设置指令为0.1 s时1 mm的位置阶跃信号，仿真EMA1位置传感器反馈参数在-1%～1%偏置下的静态力纷争情况。

(2)保持2个作动器无位移输出，负载力从-4 kN到4 kN缓慢变化。EMA1通道连接刚度为1.1×108N/m，EMA2连接刚度为1.0×108N/m。

根据2.1节中的理论分析，静态位置误差导致的静态力纷争情况应当符合式(8)：

(8)

因此静态力纷争γ如式(9)所示:

γ=F1-F2=kL(0-E1)=-kL·E1

(9)

由于连接刚度不一致导致的静态力纷争情况应当符合式(10)：

(10)

由图4可以看出：静态位置误差以及负载力大小对静态力纷争的大小影响呈线性关系，其中静态位置误差造成的影响较大，而连接刚度不一致对静态力纷争产生的影响较小，但在大负载状态下仍不可忽略。由此理论分析也得到了验证。

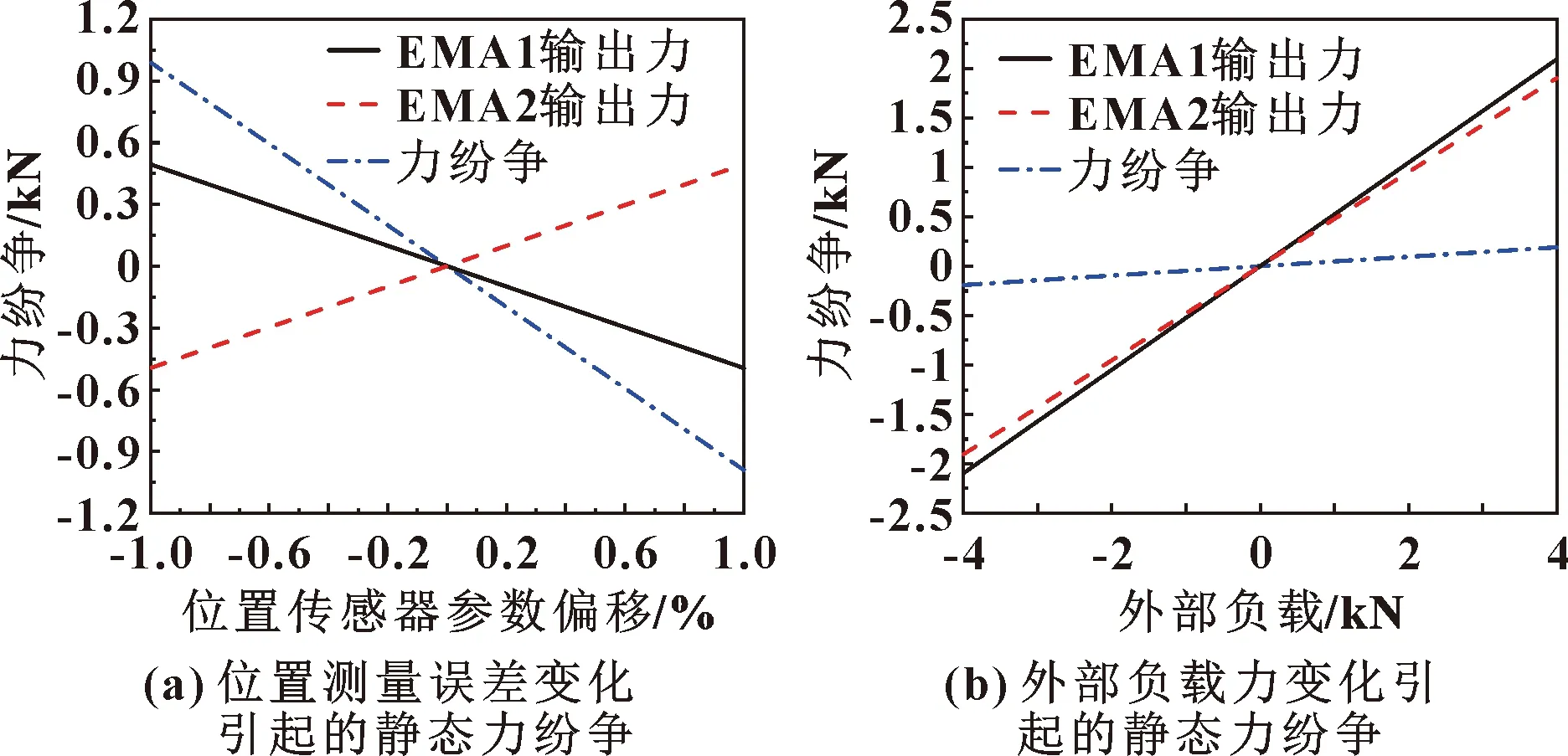
图4 静态力纷争

3 静态力均衡控制技术设计

由上节可知，EMA的输出力主要由2个因素决定，其中因为连接刚度无法轻易改变，因此选择调节静态位置偏差来缓解静态力纷争。

因此，文中设计了一个力均衡控制器，它通过补偿各个通道中的位置反馈来改变位置误差，从而消除静态力纷争。静态力均衡控制方法如图5所示,由此，将式(7)调整为

kL1·F1+E1=kL2·F2+E2+ECO

(11)

其中:ECO为补偿的位置偏差量。

图5 静态力均衡控制方法

消除静态力纷争的过程其实就是消除稳态误差的过程。根据经典控制理论，设计了2种控制器，并进行仿真验证和分析。根据第2节的分析设置统一的仿真条件和指令以模拟静态力纷争的情况。

条件：通道1连接刚度为1.1×108N/m,通道2连接刚度1.0×108N/m，位置传感器参数偏置1%。

指令：0.1 s时刻输入1 mm的位置阶跃指令，4 s时输入8 kN的阶跃负载力。这里用8 kN是为了提高连接刚度不一致产生的静态力纷争。

3.1 积分环节的力均衡技术

积分控制因长期、低频的效果以及对动态性能影响小，可以减少各种响应的稳态误差等特点，已被应用在其他类型作动器系统的力均衡技术上[15]。图5中的控制器表达式为kI/s，其中kI为积分系数。

当力纷争产生时，其值经过积分控制器后变为位移补偿量，加入到通道的反馈回路中最终改变作动器的实际输出位移量，并且该补偿量逐渐累积直至没有力纷争，2个通道最终补偿值的总和为式(11)中的ECO。下面仿真分析了它在双余度机电作动系统中的力均衡效果，仿真结果如图6所示。

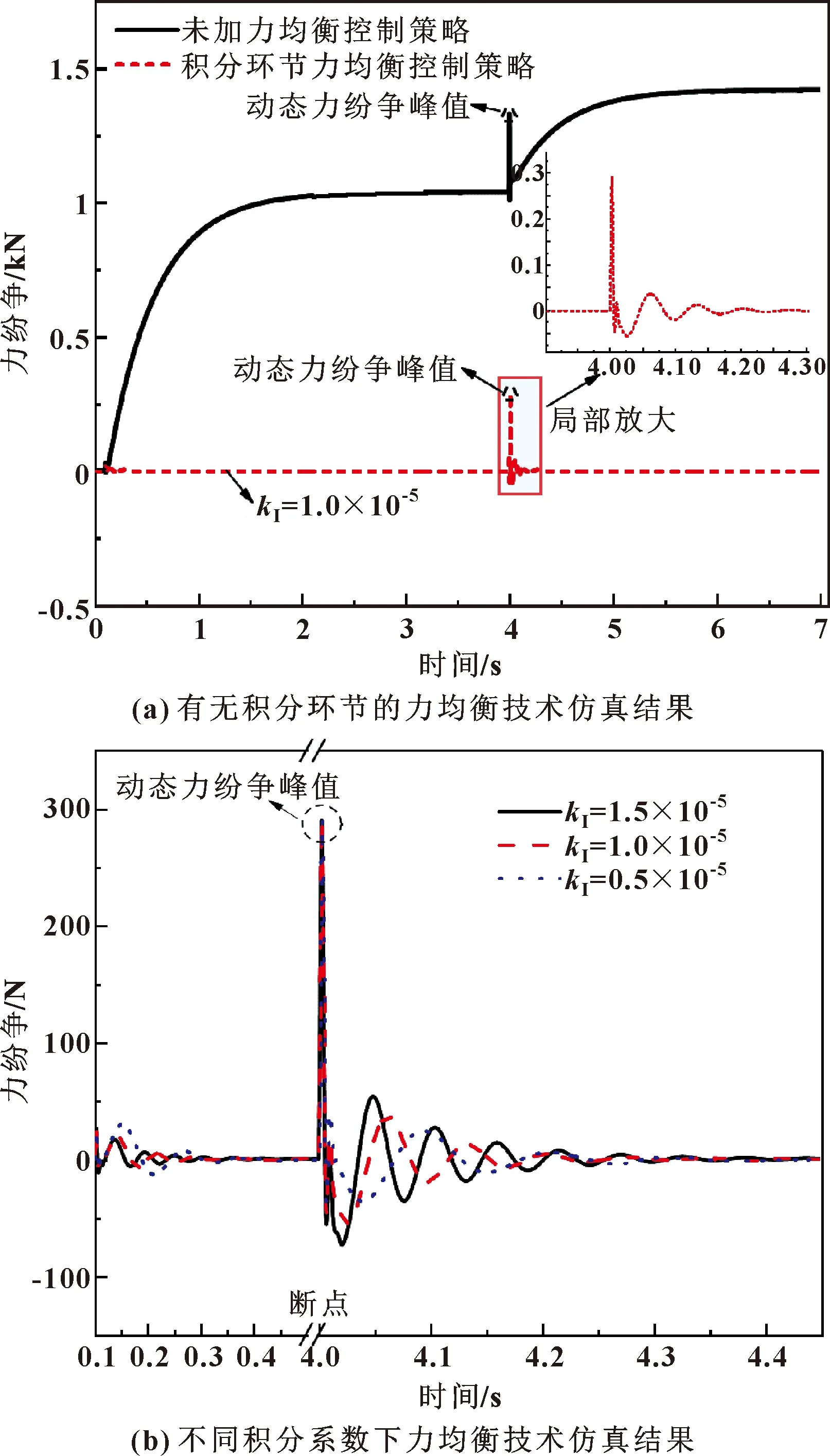
图6 积分环节力均衡技术仿真

通过调参确定了积分环节中系数项kI的取值范围。从图6(a)可以看出，加入了积分环节的力均衡控制方法后，静态力纷争得到了消除。要注意的是，4 s时刻产生了一个由于负载阶跃引起的动态力纷争峰值，这一部分不在静态力均衡的讨论范围里，因此不对该部分进行分析。

进一步观察图6(b)中3种系数下的积分环节控制方法的对比，可以看出：积分环节使得静态力纷争得到了消除，动态力纷争的大小也在可接受范围内，但其振荡时间较长。此外，在无负载的位置跟随状态下，kI越小，振荡的幅度越大。而在负载状态下，忽略动态峰值，kI越大，其力纷争的振荡越剧烈。因此，积分环节系数的大小让力纷争在2种状态下的稳定性表现上是相反的。综上，纯积分环节的力均衡技术可以很好地消除静态力纷争，但是在快速性上较差、动态时间较长。

3.2 比例积分环节的力均衡技术

针对传统积分环节力均衡控制方法在快速性上的弱点，增加比例环节对其进行改进。图5中的控制器表达式变为kP+kI/s。

仿真选取kP=0.5×10-6，kI=1.0×10-5。并且对比纯积分环节kI=0.5×10-6的力均衡控制方法，结果如图7所示。

图7 2种力均衡技术对比

从图7中可以看到：比例环节会对力纷争迅速作出反应，以减小偏差，并加快这一进程；而积分环节使得它能够消除稳态误差，使静态力纷争为0。此外，忽略初始时刻短暂的动态力纷争峰值，其稳定性也优于纯积分环节的力均衡技术。

3.3 总结

纯积分环节的静态力均衡控制技术可以很大程度上消除静态力纷争，但是其系数值的选取需要兼顾系统位置跟随和抗负载扰动状态下的表现，并且在快速性上较差、振荡时间过长；改进后的比例积分环节力均衡技术在选取适当的系数值后，可以较快较稳定地消除该系统的静态力纷争。

4 结论

此研究主要得到以下主要结论：

(1)双余度EMA中产生静态力纷争的两大主要因素为通道间产生的静态位置偏差以及通道间连接刚度不一致，并且其影响可以叠加。

(2)传统积分环节的力均衡技术可以消除该系统的静态力纷争，但存在快速性差、振荡时间过长的问题。经过改进后的比例积分环节的力均衡技术很好地解决了上述问题。

(3)静态力均衡技术无法解决在系统某些条件下的动态力纷争峰值问题，也无法避免动态上的振荡现象，需要进一步研究动态力均衡控制方法。