基于粒化散布熵和SSA-SVM的轴承故障诊断

叶震，李琨

(昆明理工大学信息工程与自动化学院，云南昆明 650500)

0 前言

滚动轴承由于其运行环境常处于高速、高载、高温状态下，导致各种故障频发。对于轴承振动信号非平稳、非线性特性，如何更丰富、更全面地提取出信号中的深层故障信息显得尤为重要。熵值是提取特征信息的方法之一，被广泛应用于各种模式识别中，如样本熵[1]、近似熵[2]、模糊熵[3]和散布熵[4-5]等。但上述方法仅从单一尺度对时间序列复杂程度进行刻画。而针对机械系统故障诊断问题，振动信号往往过于复杂，此时单一地对它进行信号特征提取存在着信息表达不足、无法全面概括不同故障类型特征信息的问题，从而无法准确诊断机械系统故障。同时，散布熵值的求解局限于待求解时间序列的信号特征，有必要在单一尺度散布熵的基础上，对振动信号进行深层次故障信息提取。因此，本文作者提出模糊信息粒化-散布熵(Fuzzy Information Granulation-Dispersion Entropy,FIG-DE)的方法，从多个尺度有效提取轴承振动信号的故障信息。

在信号故障特征提取的基础上,选择合适的诊断模型也尤为重要。支持向量机(Support Vector Machine，SVM)适用于处理小样本和非线性问题，凭借其学习效率高及泛化性能好等优点，已经广泛应用于故障诊断、模式识别等众多领域。但其惩罚系数c和核函数参数g的取值影响算法的分类性能。张小龙等[6]利用粒子群优化(Particle Swarm Optimization，PSO)算法搜索出SVM的最优参数，有效提高了滚动轴承的分类准确率。戚晓利等[7]利用灰狼优化算法优化SVM，在行星齿轮故障诊断上取得了较好的效果。但这些方法优化效率低，迭代时间较长且诊断精度不高。麻雀搜索算法(Sparrow Search Algorithm,SSA)是在2020年提出的一种优化算法。SSA算法在搜索精度、收敛速度、稳定性和避免局部最优值方面均优于现有算法[8]。

基于此，本文作者利用模糊信息粒化对轴承振动信号进行粒化处理，得到fLow、fR、fUp3个尺度下的模糊信息粒，对3组信号从3个尺度下分别求取散布熵并作为特征向量输入，由麻雀搜索算法(SSA)优化的SVM模型，实现滚动轴承的故障诊断识别。

1 模糊信息粒化

美国数学家ZADEH[9]教授提出的信息粒化(Information Granulation,IG)的概念，就是将一个整体时间序列多尺度粒化为一个个的部分进行分析研究。对于轴承振动信号而言，可以根据故障信息特点把信号划分为若干个信息粒来提取信号特征。关于模糊信息粒化方法,给出了数据粒的一种命题描述：

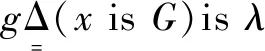
(1)

式中：x为论域U中取值的变量；G为U的凸模糊子集，由隶属函数μ刻画；λ为可能性的概率。一般定义U为实数集合R(Rn),λ为位区间的模糊子集。

模糊信息粒化就是以模糊集形式表示信息粒,含粒化窗口和信号模糊化两个部分。粒化窗口指的是将信号序列分割截取成若干子序列，作为操作窗口；信号模糊化即为将分割的子序列进行模糊化,得到模糊集(模糊信息粒)。

梯形、三角形、高斯型等是常用的模糊粒子，现有关于FIG应用的文献[10-12]大多采用三角形粒子，因此文中也以三角形模糊粒子作为隶属函数:

(2)

式中：x表示划分的粒化信号；l、m、n分别表示粒化窗口内数据变化的最小值、大致平均水平和最大值。

2 散布熵理论

散布熵是描述时间序列复杂程度的非线性动力学方法。对于长度为N的时间序列x={xi|1≤i≤N}，首先使用标准正态累计分布函数将x归一化为yi= [y1,y2,…,yN],yi∈(0，1)。进一步，将y映射到c个类别：

(3)

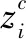
对映射序列zc按如下公式相空间重构：

(4)

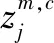
计算πv0v1…vm-1的概率：

(5)

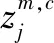
根据信息熵理论定义散布熵为

(6)

sDE值越大，时间序列的不规则性越高；相反sDE值越小，不规则性越低。

3 SSA-SVM算法

3.1 SSA算法

麻雀搜索算法是在2020年提出的一种新型优化算法。SSA算法的寻优步骤主要分为3个部分：

(1)发现者寻找并引导整个麻雀种群觅食。

发现者在每次的迭代过程中位置按如下公式更新：

(7)

式中：Xi，j为麻雀i在第j维中的位置信息；t为当前迭代次数；tmax为最大迭代次数；α∈(0,1]为一个任意数；Q为服从正态分布的随机数；L为d维列向量，元素均为1；R2∈[0,1]为预警值；fST∈[0.5,1]为安全值。

(2)追随者是根据发现者所引导的新位置进行觅食，在整个麻雀种群中，发现者与追随者的位置是实时更新的，只要追随者找到好的食物就能称为发现者，反之成为追随者，但其数量比重是不变的。

追随者在每次的迭代过程中位置按如下公式更新：

(8)

式中：XP为当前发现者所占据的最优位置；Xworst为当前全局适应度最差的位置；A∈{0,1}为d列向量,且满足A+=AT(AAT)-1，其中A+为伪逆矩阵。当i>n/2时,表明适应度较低的追随者i无法获取食物，需要更新位置寻找食物。

(3)在整个麻雀种群中，定义警惕者占总数量的10%～20%，且警惕者的初始位置是在种群中随机分布的，当警惕者意识到周围存在捕食者时，外围的麻雀将快速地向安全的地方飞行，来获取较好的搜索环境；内部的麻雀将在安全的区域内觅食。

警惕者在每次的迭代过程中位置按如下公式更新：

(9)

式中：Xbest为当前全局适应度最优位置；β为服从正态分布的随机数，起步长控制的作用；K∈[-1,1]，是一个随机数,表示麻雀种群位置移动的方向，同时也起到步长控制的作用；fi为当前个体的适应度值；fg、fw分别为当前全局最优和最差的适应度值；ε为最小的常数。当fi>fg时，外围麻雀发现了捕食者；反之区域内的麻雀发现捕食者。

3.2 SSA-SVM参数优化

SVM是一种常用的模式识别方法，具体理论见文献[13]。惩罚因子c及核函数参数g的取值密切影响着SVM算法的性能，本文作者提出利用SSA算法对SVM进行参数优化，对最优参数设置下的SVM模型进行故障分类识别,流程如图1所示，具体的实现步骤如下：

(1)获取滚动轴承不同故障程度的振动信号处理后划分为训练集和测试集；

(2)SSA参数初始化。设置种群规模、最大迭代次数N，设置参数c和g的取值范围为[0.01，50]，选用高斯核函数；

(3)按照式(7)—(9)更新麻雀的空间位置；

(4)利用适应度函数重新计算优化后各麻雀的个体适应度，更新并保存当前种群中最优的麻雀个体位置及适应度；

(5)若满足运算终止条件，则结束优化，输出适应度最优的麻雀个体所对应的位置，即为最优参数c和g，否则继续循环。

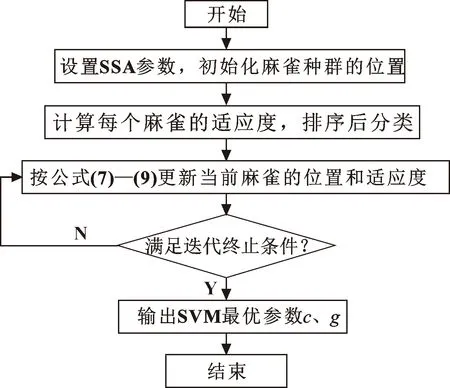
图1 SSA-SVM流程

4 实验分析

4.1 故障诊断流程

将信号模糊信息粒化处理后，得到3组信号序列fLow、fR、fUp。求取这3组数据的散布熵，组成特征向量输入SSA-SVM模型中，完成滚动轴承的故障诊断识别，诊断流程如图2所示。具体诊断步骤如下：

(1)选取合适大小的预设粒化窗口对原始轴承振动信号进行模糊信息粒化，得到fLow、fR、fUp3个尺度下的粒化数据。

(2)对3组粒化序列进行量化处理，设置DE参数，求取粒化后3组数据的散布值，构建特征向量矩阵。

(3)取特征向量的1/2作为训练集对SSA-SVM模型进行训练，再利用训练完成的SSA-SVM模型对剩余部分特征向量进行故障识别，从而实现轴承故障诊断分类。

图2 故障诊断流程

4.2 参数选取

基于文中所提出的FIG-DE的特征提取方法，对粒化后的3组fLow、fR、fUp求取散布熵值，可以提取更为丰富的故障特征信息。但在FIG-DE的特征提取的过程中，参数的取值也尤为重要。

在模糊信息粒化数据划分粒化窗口时，窗口的取值不宜过小，当粒化窗口为1时，则为直接对振动信号求取散布熵，失去了粒化的意义；当粒化的窗口过大时，会导致粒化后的时间序列长度过短，且会失去部分较为重要的信号特征。因此文中初始化粒化窗口win_num为3。

在DE值的计算过程中，需要定义3个参数：映射类数c、数据维数m、时间延迟t。参考文献[14-15]，选取时间序列的映射类别参数c=6，时间延迟t=1；针对嵌入维数m越大，对应所需的数据长度越长的问题，综合考虑选取m=3。

4.3 实验数据分析

选用公共数据集——凯斯西储大学电气工程实验室的轴承故障振动信号进行仿真实验。选用转速为1 797 r/min、采样频率为12 kHz时轴承不同故障类型和故障程度的振动信号作为数据样本。取每种故障类型的前120 000个采样点平均分为40个数据样本，每个样本的数据长度为3 000个采样点，为分析方便，分别以代码F1—F7的形式表示故障类型，其具体信息如表1所示。不同故障类型的时域波形如图3所示。

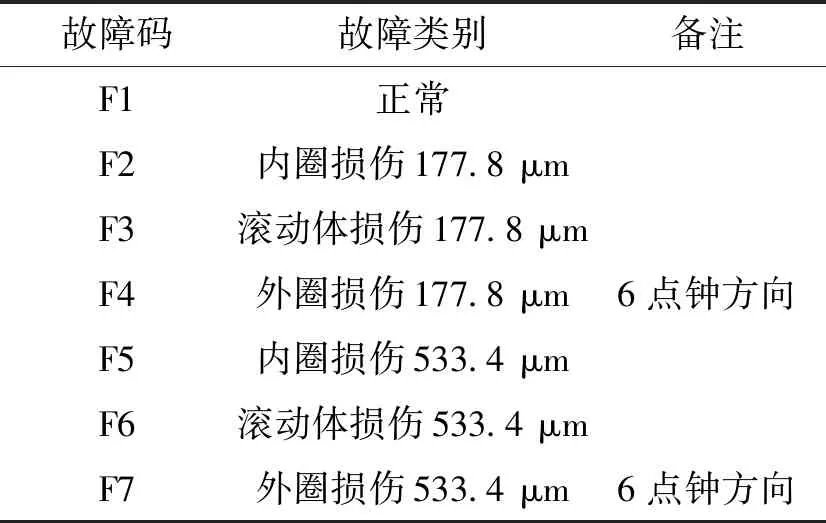
表1 轴承的故障码和故障类别

图3 7种状态的时域图

首先，对轴承各种状态的振动信号进行模糊信息粒化处理。以F1的振动信号为例，设置窗口长度win_num为3，经模糊信息粒化后数据长度由3 000变为1 000，在一定程度上明显优化了对信号的处理效率，信号经过粒化处理后得到3组数据序列fLow、fR、fUp。模糊信息粒化结果如图4所示。

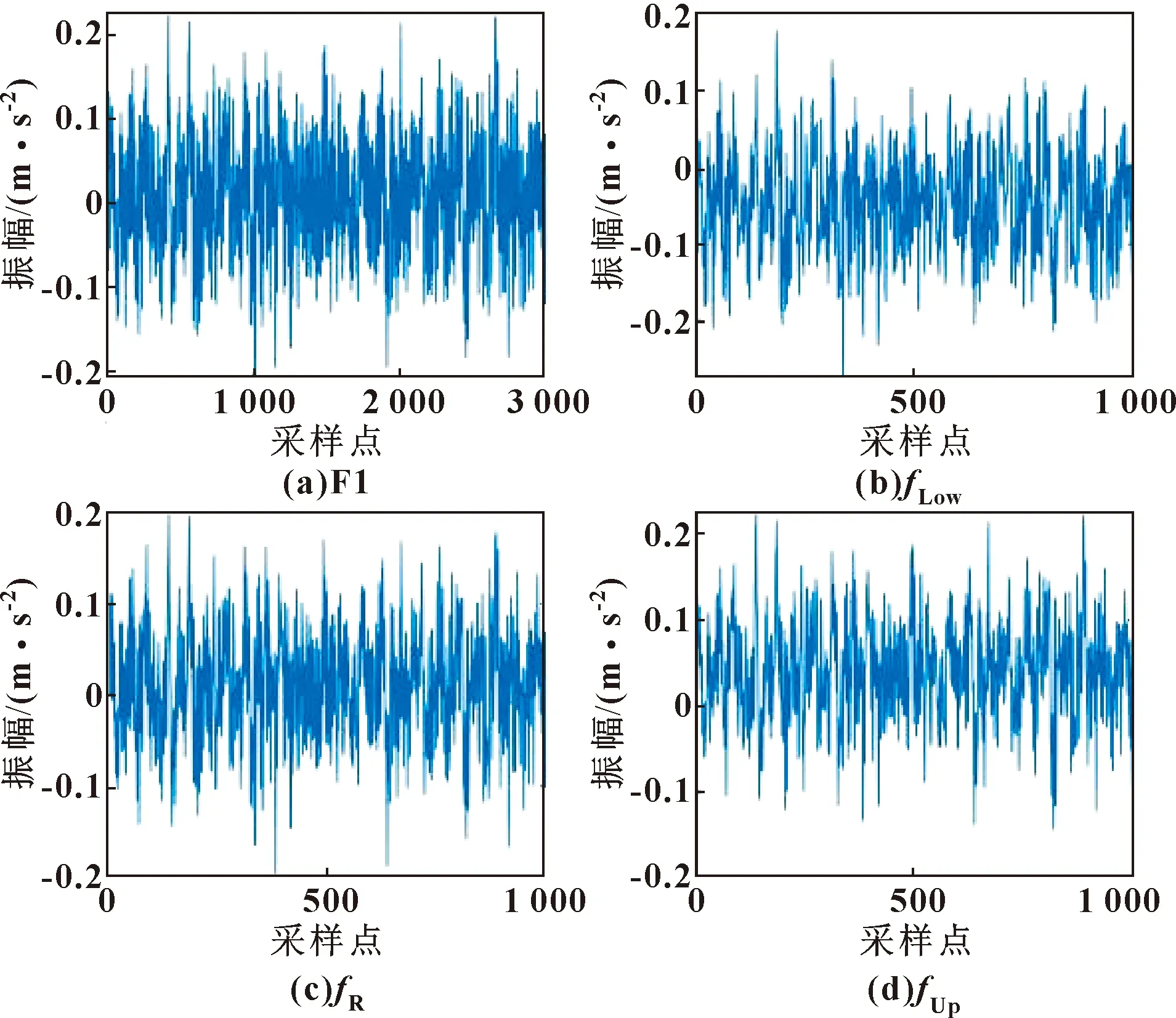
图4 信号模糊粒化结果

由图4可知：经过粗粒化后的滚动轴承故障振动信号，通过fLow、fR、fUp3组具有更明显特征的模糊粒化数据，弥补了滚动轴承故障振动信号在单一尺度下提取故障特征信息不全的问题。粗粒化的时间序列保留了原始振动信号的特征信息，同时用3组模糊粒子对特征信息进行了深层次刻画，提高了对原始振动信号故障特征信息的提取能力。在粒化窗口win_num为3的条件下，对3个尺度下的fLow、fR、fUp分别进行DE求解，并将所求得的熵值组成特征向量矩阵:

V=[fDE,Low,fDE,R,fDE,Up]

(10)

为进一步体现所选特征向量的可分性，将计算所得7组40×3的DE值进行可视化，其三维散点图如图5所示。

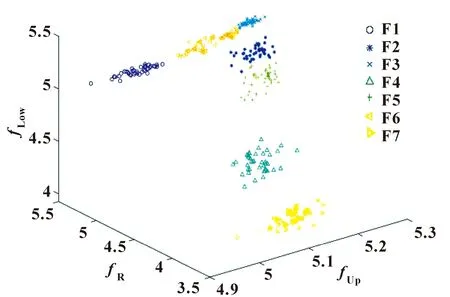
图5 FIG-DE的三维散点图

由图5可知：不同故障类型的数据样本呈现出较好的分离状态，各数据样本之间基本无交叉混叠现象，这表明滚动轴承振动信号经FIG-DP特征提取后所取得到的特征向量具有良好的区分度。

为量化采用FIG-DE进行故障特征提取的效果，建立SSA-SVM模型进行轴承故障诊断识别。SSA-SVM模型分类器的参数设置如下：麻雀初始种群为20，最大迭代次数为100，惩罚因子c和核函数参数g的寻优范围设定为[0.01,50]。将训练集输入至SSA-SVM模型中进行训练，经过优化后，c和g的最优参数分别为15.23和0.41，然后对训练完成的SSA-SVM模型使用测试集进行测试，测试效果如图6所示。

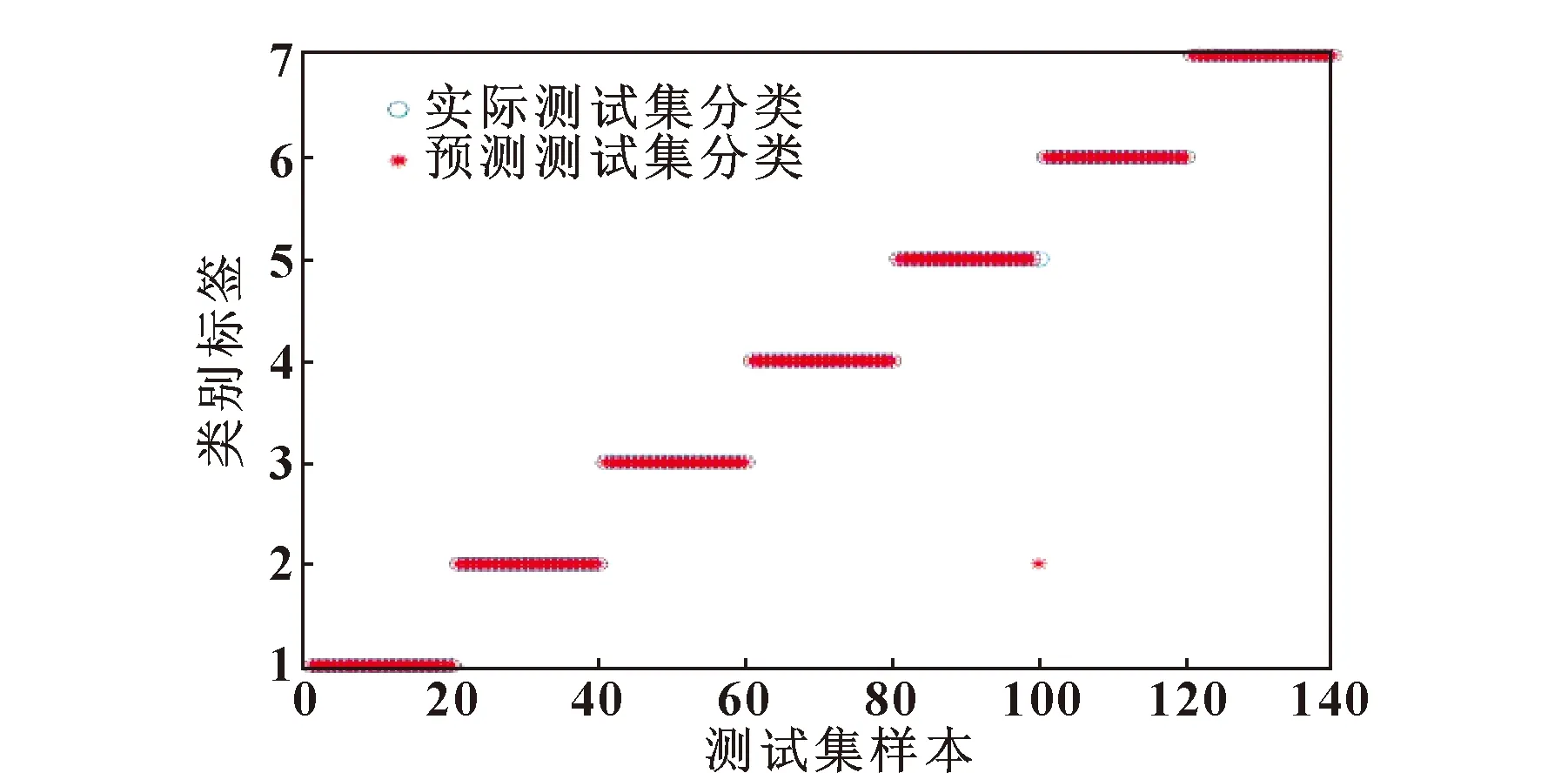
图6 基于FIG-DE与SSA-SVM诊断结果

由图6可以看出：所有测试样本类别基本上都得到了准确分类，实际故障结果与预测故障结果基本完全吻合，故障识别准确率达到了99.29%，这表明文中所提方法不仅能正确判断出轴承故障位置，还能准确识别出故障的损伤等级。

为验证SSA-SVM故障分类器的优越性以及高效性，使用PSO-SVM、GWO-SVM和SSA-SVM分别进行故障类型识别，3种模型统一设置种群数量为20，最大迭代次数为100，其各自的适应度迭代曲线如图7所示。可知：PSO-SVM优化算法容易陷入局部最优；GWO-SVM优化算法在第30代左右趋于稳定，其寻优结果和收敛速度均低于SSA-SVM优化算法；SSA-SVM优化算法在第20代左右即寻优结束，其收敛速度快并且可以得到更好的寻优结果。

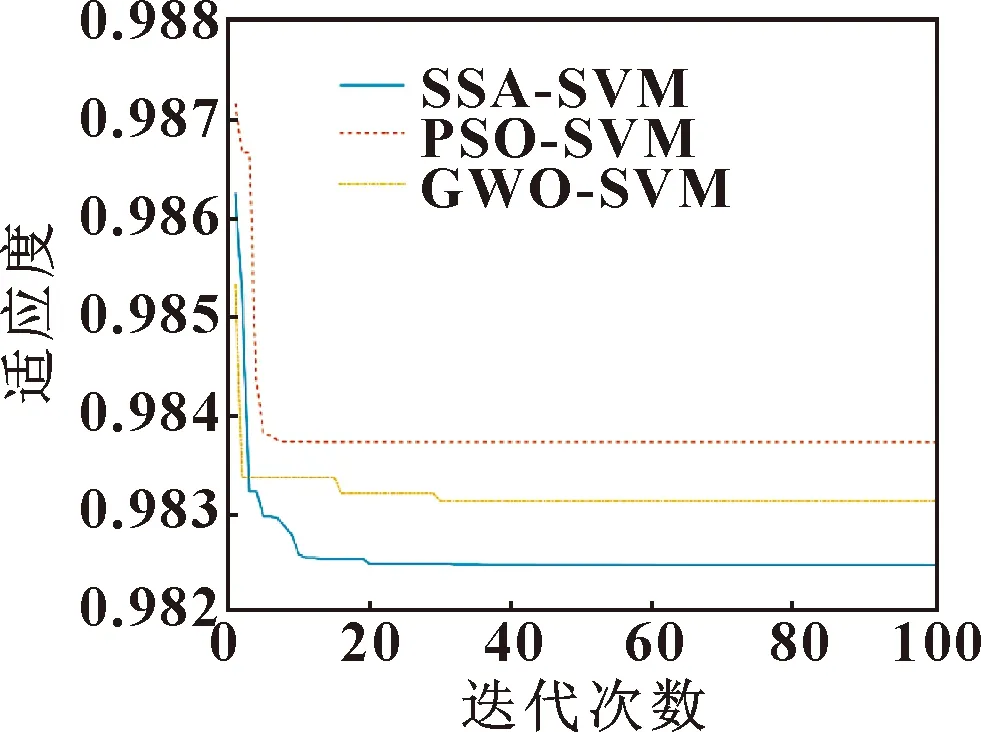
图7 分类适应度寻优曲线

经3种模型搜索出适应度最优对应的c和g设置为SVM参数并进行训练，训练完成后输入测试集进行测试，c和g的优化及3种模型的测试结果如表2所示。可知：不同优化方法得到的c和g的值不同，其中SSA-SVM模型的优化效果最好，测试准确率可达99.28%，与PSO-SVM及GWO-SVM模型的优化效果相比，在分类准确率上分别提高了2.85%和0.7%；在优化时长上，SSA-SVM模型所需迭代时间为2.53 s，明显优于其他2种算法，且分类错误数量仅为1，这充分表明了文中所提SSA-SVM方法在同类优化支持向量机模型中效果更佳。

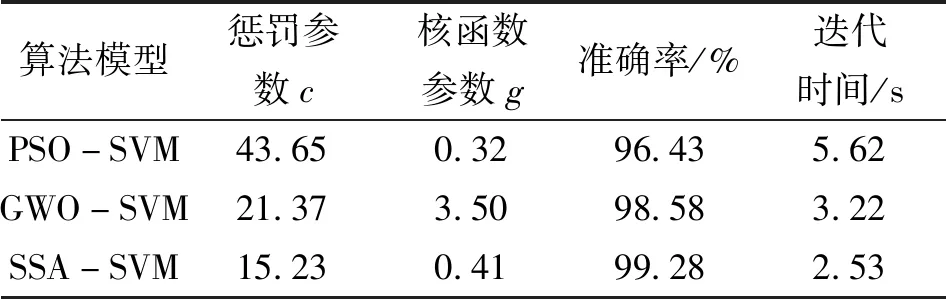
表2 轴承的故障码和故障类别

5 总结

本文作者结合模糊信息粒化与散布熵对轴承故障振动信号进行分析，提出了新的FIG-DE熵值求解方法，在多个粗粒化序列下对振动信号的特征向量进行了深层次提取。对模糊信息粒化后的振动信号求取DE值并作为特征向量矩阵，输入经SSA算法优化后的SVM进行分类诊断,取得了较好的效果。结果表明：

(1)相比基于散布熵的故障特征信息提取，FIG-DE方法通过粗粒化方式得到3个尺度下的粗粒化序列的信息，所提取的故障状态特征向量更加全面，具有一定的精度优势。

(2)FIG-DE算法简单、参数设置较少且定义了粒化窗口设置标准，经模糊信息粒化后数据长度明显缩短，在一定程度上优化了对信号的处理效率，并且所提取的特征向量仅有3组，缓解了特征向量过多造成的数据冗余问题，同时也改善了算法的自适应性。

(3)采用SSA算法优化SVM模型，可以更加准确快速地搜素出最优的惩罚参数c和核函数参数g组合，提高了SVM的分类精度。