低信噪比突发信号载波频差估计方法研究
2022-11-30李月园
李月园
(上海邮电设计咨询研究院有限公司,上海 200092)
0 引言
目前应用比较广泛的突发信号频差和检测算法主要有三种:第一种是能量检测算法,此算法主要检测信号短时能量,优点比较明显,主要表现在实现简单,同时可以在基带和中频中进行。缺点主要是对载波的频差无法准确估计[1],同时受信噪比影响比较大,不适用于低信噪比下的信号检测;第二种是匹配滤波法,此方法主要利用接收信号和本地信号的相关性完成,缺点是只能通过判决门限与信号电平来实现载波频差的估计,因此无法在高动态情况下准确估计载波频差[2];第三种是Power-Law算法,此算法的优点是可以在低信噪比下准确地检测出载波信号,缺点是计算过于复杂,无法进行实时处理。为了能够更好地实现低信噪比突发信号载波频差估计,该文提出了一种新的算法,此算法不但建立了对信号电平及频偏动态不敏感的特征量,同时还建立了能够表征信号与噪声差异的特征量。为了验证该算法的正确性,该文还进行了一系列的对比测试,测试结果表明,此方法频差估计的精度更高。
1 基本原理
1.1 构建模型
可以把突发信号的存在性检测进行模型构建,使用二元假设检测模型,此模型适用于高斯噪声环境[3],可以把接收信号等效复低通等效成公式(1)。
式中:M1为目标信号不存在,M0为目标信号存在;g(t)为复高斯白噪声;y(t)为有用信号,此信号的表达式如公式(2)所示。
式中:an表示的是发送的信息符号;sT(t)为基带发送成形滤波器的冲激响应;T表示周期;fd为载波频差[4]。
通常情况下,都是使用平方根升余弦成形滤波器。在工程应用,特别是高动态低速通信中,通信系统在高速运动的时候会出现很大的多普勒频移,多普勒频偏一般情况下和符号速率处于相同的量级[5]。
突发信号数据帧主要由两部分数据构成,一部分是前导码,另一部分是有用数据。前导码的主要功能主要由三个,第一个是实现突发信号功率检测,第二个是实现符号位同步,第三个是实现数据帧同步[6]。在使用的过程中,同构BPSK对前导码进行调制,该文提出的算法主要就是调制过的前导码进行二次功率谱变换,最终实现突发载波信号的频差估计。
1.2 算法原理
如果把不存在噪声的BPSK调制信号进行平方运算,可以表示为公式(3)。
式中:an为发送的信息符号;sT(t)表示的是基带发送成形滤波器的冲激响应;c(t)为随机信号,其表达式如公式(4)所示。
式中:an和am分别为发送的两个随机信息符号。
通常情况下c(t)还可以表示为公式(5)。
式中:v(t)为稳态波;z(t)为交变波分量。
BPSK调制信号有一个重要的特点,那就是序列{an}各符号之间都不存在相关性。当其值为+B或者-B且出现的概率一样时,就可以表示为公式(6)和公式(7)。
式中:E为随机序列;z(t)为交变波分量。
通过公式(6)可知,v(t)是一个周期信号,其周期是T。公式(7)中的z(t)表示的是交变波分量,因此可以把此信号进行傅里叶级数展开,得到公式(8)。
式中:Dm表示的是最大幅度谱分量,fk表示的是频差值。如果fk=1/T,则v(t)的傅里叶变换可以表示为公式(9)。
公式(9)中,Dm的表达式为公式(10)。
式中:G(f)=GT(f)×GT(f),如果载波信号不存在频差,对BPSK截短信号进行平方运算,结果是在频率f=m/T处的频谱会出现离散谱线,此时的幅度和|G(f)|是成正比的关系,并且幅度的极大值在零频处[7]。如果载波信号存在频差,频差的值是fk,做同样的运算后,其结果是f=2fk处存在幅度极大的离散谱分量。该文使用的方法充分利用了这个特点,先搜索出突发信号的前导头,然后再进行平方变换,最后可以得到最大幅度谱分量,实现载波信号的频差估计[8]。
2 算法实现
先对待检测信号x(t)进行采样处理,采样率设定为N/T,采样后的离散信号用x(n)表示,在进行频差估计之前必须要进行信号检测特征量的构建,具体的过程可分为五步。
第一步,把采样后的离散信号进行平方运算,如公式(11)所示。
第二步,进行离散傅里叶变换,如公式(12)所示。
式中:i=0,1,…,LN-1;w(n)为滑动窗,其长度是LN,h为采样点数,其范围是相邻两组l(n)观测窗向前滑动。
第三步,把m组的l(n)平均功率计算出来,其结果可以表示为公式(13)。
第四步,确定出Lm(i)中最大幅度谱线位置,此参数用imax表示。
第五步,确定出检测判决函数,此函数可以表示为公式(14)。
如果用η表示门限,当Tm(L)大于η时表示信号存在,反之则信号不存在。虚警概率可以表示为公式(15)。
由公式(15)可知,虚警概率不受电平信号的影响。在实际应用过程中,判决门限可以根据虚警概率进行有效调整,输入信号的电平不会产生任何的影响。
如果条件M1成立,就可以把Lm(i)最大幅度处的离散频率表示为公式(16)。
式中:[LT]为最接近l的整数,通过离散傅里叶变换粗测频率可以表示为公式(17)。
公式(17)中的分辨率是1/LT。由此可以看出粗测频率的精度受信号测量长度的影响很大,而突发信号的前导头的长度很短,所以粗测频率的精度不高。传统的算法通常会使用DFT结合插值的方式进行,这样也可以提高频率的估计精度,因此该文也使用了频率差值算法,其频差估计的表达式如公式(18)所示。
频差的估计为[-N/4T,N/4T],估计范围主要受采样倍数影响。如果N=8,频率估计在-2/T和2/T之间,此范围就可以适应大部分频率高动态情况的需要。如果出现极限状态,例如频差出现超过2倍符号率,此时可以进一步增大采样倍数,进而实现扩大频率估计范围。
3 测试结果和结论
3.1 测试结果
为了验证该算法的正确性,该文和Power-Law算法(简称PL算法)进行了一系列的对比测试,通过设置突发通信系统中的信道参数和信噪比范围进行测试,测试条件如下:sT(t)使用的是滚降系数0.35的根升余弦函数,信号的采样率设定成8/T,fd的取值范围设定为[0 , 2/T],仿真次数是5000次。设置虚警概率Pf<1%,观测长度分别设定为128、256、512,检测概率Pd(%)和信噪比关系测试结果如图1所示。
从图1的测试结果可以得出结论,信噪比比较高的时候,两种算法都能够得到比较高的检测概率。但是在信噪比较低的情况下,该文使用的新算法比PL算法检测概率更高。如果观察的长度更长,特别是在管长度为512时,优势更加明显。观测长度越长,低信噪比下的信号检测概率就越高,并且该文算法的信噪比门限可改善达到2dB。
在观测长度不一样的情况下,观测长度越长,该文算法的检测性能越明显,检测长度增加1倍,在检测概率相同的情况下,对应的信噪比门限大大降低,可以降低到1.5 dB左右。在实际的应用当中,可以根据检测概率的要求设置不同的观测长度。
在实际的工程应用中,通常对突发信号的正确检测率要求比较高,通常情况下都要求高于99.9%。根据前面的测试可知,观测长度为128时,正确检测概率99.9%对应的信噪比是3dB;观测长度为256时,正确检测概率99.9%对应的信噪比是1.5dB;观测长度为512时,正确检测概率99.9%对应的信噪比是0dB。该文算法在最小分辨率情况下,不同评率的估计精度也需要验证。为了能够进行科学的测试,设置载波频差fd=(L+δ)Δf,其中δ表示均匀分布的6个频率点,取值是0~0.5,并且取平均分布的6个频率点,各个点的测试次数为5000,频差估计性能的好坏通过归一化频率估计均方根误差(Root Mean Square Error, RMSE)衡量,此参数表达式如公式(19)所示。
测试结果见表1。
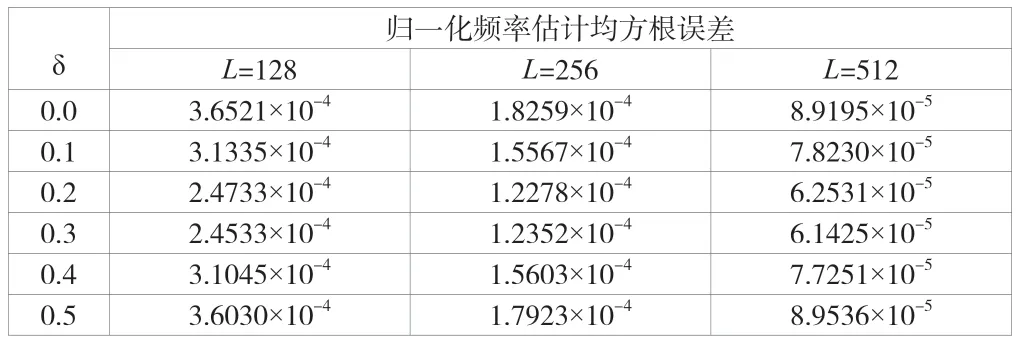
表1 频差估计测试结果
从表1的测试结果能够得到在低信噪比,且检测概率高于99.9%的信噪比门限下,RMSE的值都在1‰符号速率以下,并且观测长度的值越大,估计误差越小,观测长度每增加1倍,估计误差就会减小二分之一左右,频差估计的精度更高,该文算法在低信噪比的情况下可以完成频偏高精度估计。
该文算法和传统算法相比主要的区别有以下3点:1)该文算法能够实现直接对接收信号(此信号为匹配滤波前的信号)进行处理,并实现精确的频率估计,传统的算法需要先对接收信号进行位同步变换,使其转换成单音信号才能进行处理;2)该文算法的频率估计范围更广,在实际应用中是(-2/T,2/T),传统算法的范围在实际的应用中是(-1/2T,1/2T), 通过对比可知,该文算法频率估计范围是传统算法的4倍,还可以更高。3)该文算法在进行平方运算的过程中会出现交变波分量,这种分量不利于对频率进行精确估计,并且在进行平方运算的时候还会出现信噪比损失的情况。通常情况下,在观测长度相同的情况下,传统的方法估计精度更高一些。但是该文算法可以实现同步处理,这样对频率精度要求会更高,同时也能够很好地提高估计精度。在实际的工程应用当中,该文算法完全可以满足解调同步算法对频偏精度的要求。
该文算法的运算量主要集中在算法步骤中第一步的平方变换和第二步的复数乘法运算,与这两步的运算量相比,其他步骤的运算量基本可以忽略不计。平方变换需要多次的复数乘法运算,可以通过快速傅里叶变换实现,计算中的求模运算可以利用CORDIC算法,这样在减少运算的同时还可以提高精度。
该文算法在实现信号检测之后,虽然增加了极小的运算量,但是这样可以实现频偏的估计,并且可以通过前馈结构进行高精度频偏校正,大大提高了频偏估计的精度。传统方法都是通过判决反馈法进行大频偏粗估计,再通过位同步的运算后才能进行频率估计的运算。和传统算法相比,该文算法不需要进行大量频率槽内依次搜索判决,这样就可以略去二次频率精度估计操作,大大减少了运算量,整个运算的流程也大大简化。
3.2 结论
该文提出了一种低信噪比突发信号载波频差估计新算法,该算法以增加极小运算量为代价换取了频差估计精度的大幅度提高,其优点比较明显,主要体现在:1)该算法虚警概率不受电平信号的影响,判决门限调整非常方便。2)频差估计的范围调整非常方便。3)只要进行一次离散傅里叶变换就可以实现载波信号的高精度频差估计,运算简单,并且可以进行实时处理。该算法具有较强的实用价值。
