基于电子传动比的多边形轴类零件数控车床工作原理及其误差分析
2022-11-29倪明威罗红波
倪明威,罗红波
基于电子传动比的多边形轴类零件数控车床工作原理及其误差分析
倪明威,罗红波
(四川大学 机械工程学院,四川 成都 610065)
多边形轴类零件具有无键连接的特性,在许多传动场景中应用甚广,但传统加工方法存在精度低、效率低等缺点。近年来提出了两轴同向转动车削加工多边形轴的方法,本文旨在根据该方法减小数控车床在车削加工多边形轴时产生的平面度误差。基于多边形轴的成型原理,建立刀尖轨迹几何模型并分析得出了刀尖的轨迹方程,将刀尖轨迹方程代入MATLAB仿真得到了不同边数的多边形轴截面的仿真轨迹。对仿真轨迹进行几何分析后得到了截面直线度误差的表达式,即可以在实际加工通过调整加工参数来获得符合要求的加工误差。根据以上方法,最后得到了不同边形满足项目要求的平面度误差(不超过0.025 μm)所需要的加工参数。
电子传动比;多边形轴;误差分析;MATLAB仿真
多边形轴类零件常应用于高转速、传递较大扭矩等加工场景中,目前在航空、航天、发电等设备制造中关键零件应用较多。现有的数控机床加工工艺是回转体表面在数控车床上加工、多面体表面在数控铣床上加工,其缺点一是工件需二次装夹、带来定位误差,二是难以达到高精度零件回转体表面与多面体表面的位置精度要求、同时降低加工效率。另一种方案则是用车床通过回转运动加工多边形轴类零件,其截面成型原理为内摆线原理,将车床上固定的刀架通过齿轮组与车床主轴连接,使其能与车床主轴同向转动,车刀刀尖在工件截面上形成内摆线的轨迹,可以近似地看作是正多边形截面,该方法实现了连续加工,但由于其成型运动是回转运动,刀尖运动所形成的截面必然是曲边多边形,与理想的多边形截面存在误差。
在误差分析方面,已有对CA6140机床进行了改进的先例,由伺服电机直接驱动刀盘,并引入了编码器对刀盘的转速进行反馈控制,验证了回转车削多边形轴类零件的原理正确性,但其直线度误差较大,还有改进的空间[1-2]。也有从摆线方程入手的尝试,分析各个参数对于摆线形态及摆线直线度误差的影响,最终得到了一组合适的参数,通过仿真加工出截面形状为正六边形的轴,其直线度误差0.018 mm[3]。由此可见,车床同向回转加工多边形截面轴类零件的原理是正确的,且其直线度误差是能够通过分析参数来进行优化。
本文通过建立平面直角坐标系,分析刀尖运动轨迹并建立刀尖轨迹方程。借助MATLAB建立刀尖的仿真轨迹,在轨迹方程中寻求两回转轴中心距与刀具回转半径的关系式,并通过该关系式得出加工出各正多边形截面的直线度误差不高于0.025 μm时所需要满足的条件。
1 多边形截面的车削成型原理
1.1 建立刀尖轨迹运动模型
两个轴同时转动并不方便建立坐标系进行轨迹分析,所以通过转化运动,将工件轴中心作为基点,将刀具轴的运动视作一边做自转一边围绕基点做公转的运动,这样就能建立如图1所示的平面直角坐标系,图中:原点1是工件回转中心、其转速为1;2为刀具轴回转中心、其转速为2;转速比可表示为=2/1,即工件轴旋转一圈、刀具轴旋转圈;为工件在单位时间内转动的角度,根据转动方向不同,存在正负之分,此处规定工件逆时针转动方向为正;为刀尖;为刀具轴与工件轴之间的中心距;为刀具的回转半径。根据该坐标系可以分析得出刀尖的运动轨迹及求得该轨迹的参数方程。
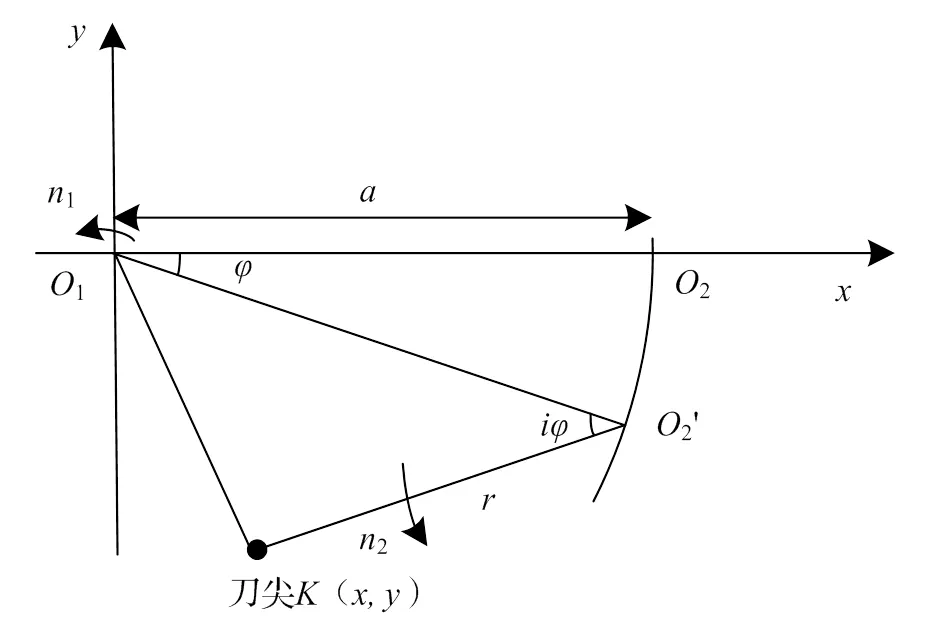
图1 平面直角坐标系中的刀尖轨迹
根据建立的平面直角坐标系可以得出刀尖的移动轨迹是内摆线。内摆线的形成原理是一个小圆内切一个大圆,且小圆绕大圆做无滑动的滚动,绕大圆滚动一周后,小圆上的一点所形成的轨迹就是内摆线,内摆线的轨迹并不是固定的,而是随着大圆和小圆的半径比的变化而变化的[4]。
刀尖相对工件中心1运动的轨迹方程为:

刀尖轨迹的几何推导如图2所示,在建立的平面直角坐标系(图1)中添加三条辅助线:第一条以O2'为起点,做平行于O1O2的平行线,交y轴于点A,交O1K于点B;第二条仍然以O2'为起点,做垂直于x轴的垂线,交x轴于点D;第三条以K为起点,做垂直于AO2的垂线,交点为C。
根据几何关系,可得到的已知条件有12'=、∠12'=。根据传动关系,传动比为,所以可得∠2'=∠12'∠12'=(1)。在△12'、△2'内运用三角函数可以求得线段2'、、1、2'的长度为2'=sin、=sin(1)、1=cos、2'=cos(1)。求出上述线段的长度后,根据几何关系不难看出,点的纵坐标的绝对值是线段与2'的和、横坐标的绝对值是线段1与2'的差,即:

根据该轨迹方程能得出,刀尖转动后形成的位移角为:

由此便得出了刀尖的运动轨迹以及参数方程,在理想情况下,只要回转半径足够大,内摆线的每条边都能视作是一条直线,也就实现了正多边形截面轴的近似加工[5]。
1.2 机械传动比方案与电子传动比方案
多边形截面轴的成型原理是将两轴同向且转速成比例旋转时,刀尖所形成的内摆线轨迹看作是多边形截面,传统方法实现同向成比例转速转动的原理是通过齿轮组传动实现的,一对齿轮啮合会使连接齿轮的两轴转向相反,但只需要在带动工件轴转动的主动轮与带动刀具轴转动的从动轮之间增加一个齿轮,就能实现两轴同轴转动,而车床主轴和刀具轴之间的转速比则可以根据三个齿轮之间的传动比来确定,在需要改变传动比时可以通过切换啮合齿轮来改变传动比关系(即换挡),但因为传动比由齿轮齿数比决定,所以改变传动比的范围有限。
随着数控技术的发展成熟,也有采用数控技术与反馈调节原理来实现同向成比例转速转动的方案,通过数控系统来同时控制工件轴和刀具轴的转向和转速,并引入反馈系统来实时监控调节两轴的转速比,将工件轴与刀具轴的转速维持为一个恒定比值[6]。原理如图3所示。
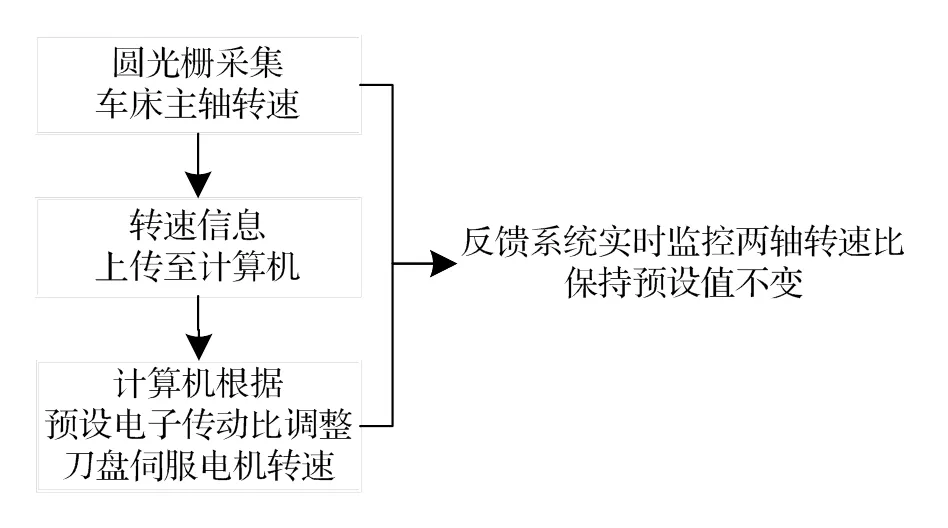
图3 保持电子转速比的流程
电子传动比方案相比于机械传动比方案,具有更高灵活性,调节传动比范围更大,可根据实际需求来进行调节,且改变传动比时无需停车换挡,具有更高的加工效率与加工精度[7]。
2 MATLAB仿真刀尖轨迹
为了得到更加直观的刀尖轨迹模型,在做参数分析之前运用MATLAB中的函数工具箱对刀尖形成的内摆线轨迹进行仿真。这也是最常用的将工程问题转化为数学模型来进行分析求解的思路,数学模型仿真具有更好的可靠性,对于快速求解、求得最优解都有极大的帮助。
采用MATLAB求解刀尖轨迹时用到的数学模型即上文分析得出的刀尖轨迹方程式(1)。为分析得到具体轨迹,此次仿真采用MATLAB自带函数工具箱中的ezplot函数,该函数能够根据给出的函数关系式自动绘制出函数的轨迹,无需给出具体的定义域。
根据ezplot函数,输入如下程序:
S=ezplot(‘x=acosθ-rcos[(i-1)θ]’,‘y=asinθ+rsin[(i-1)θ]’,[0,2*pi])
Set(S,'color','k')
规定工件转角的取值范围为0~2π,即工件转动一周时刀尖运动形成的轨迹,式中、、都可以根据实际加工时的需求来给定具体数值。图4是截面形状分别为三角形与正六边形的仿真图形。

图4 不同截面的仿真图形
另外,当中心距和回转半径二者比值一定时,无论二者数值如何变化,内摆线轨迹是保持不变的,如果能够找到一个合适的比值让刀尖形成的内摆线轨迹每条边的直线度误差符合要求,那么则能够根据这一比值与实际加工场合来对中心距和回转半径进行调整。同时通过刀具沿工件轴线移动即可成形截面为多边形的平面。
3 多边形截面直线度误差分析
3.1 多边形截面直线度误差计算[8]
根据内摆线的成型原理以及具体的轨迹参数方程可以得出:当刀具的回转半径越小,就会使得内摆线的每一条边的凹陷程度越大,所以在特定参数条件下,可以将内摆线的每一条边的曲率半径增加到足够大,就能将内摆线的每一条边都近似地认为是直线,内摆线就能近似地看作是一个正多边形,但这样的近似思想便会使正多边形轴截面的每条边产生直线度误差,进而影响到每个面的平面度误差。
误差分析的原理如图5所示。可知,刀尖通过加工形成的实际轨迹是一个凹边内摆线,它与理想情况下的正多边形是存在误差的,取其中一条边进行分析,建立了如图所示的平面直角坐标系,使曲线关于轴对称,弧和直线分别与轴有一个交点,令其分别为和,那么显而易见的是,线段的长度就是实际轨迹和理想轨迹之间的加工误差了,分析得出这样的结果后,问题便转化成了通过几何关系求出线段的长度。
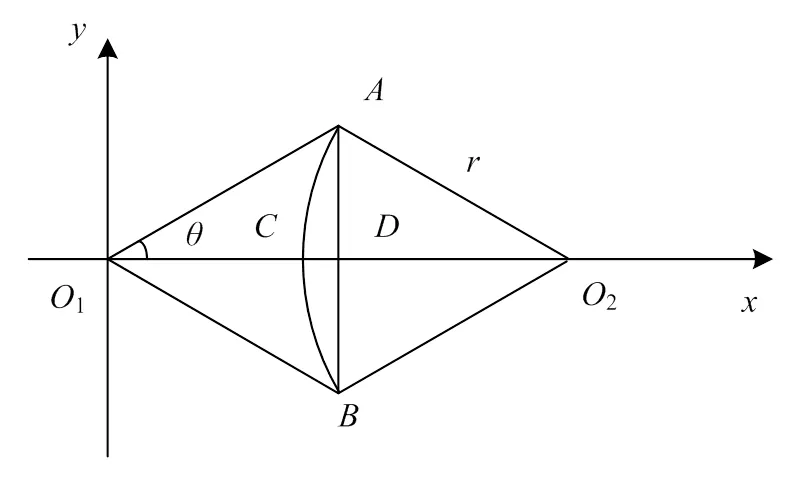
图5 截面误差示意图
误差计算以正六边形为例,图5中的点和点是成型截面中的顶点,设工件轴逆时针转动为正方向转动,那么刀尖在点时的位移角∠12=,由正多边形的几何性质可知=π/(为正多边形的边数),结合轨迹分析时得到的结论可知:
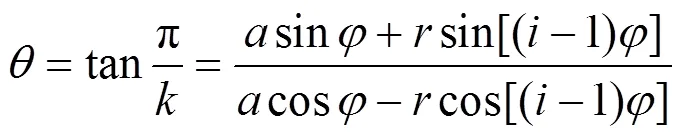
展开可得到:
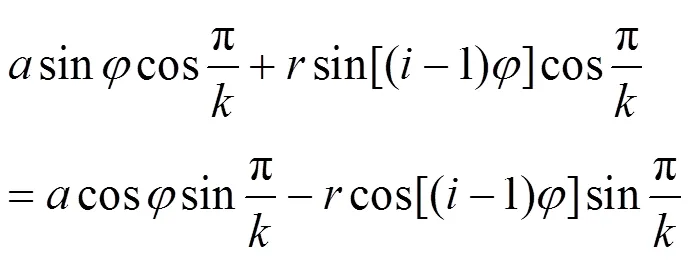
式(5)调整位置化简后,可以代入辅助角公式再化简得到:
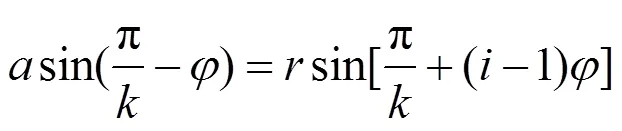
在图1中,对△12'、边12'、与边2'使用正弦定理可得:
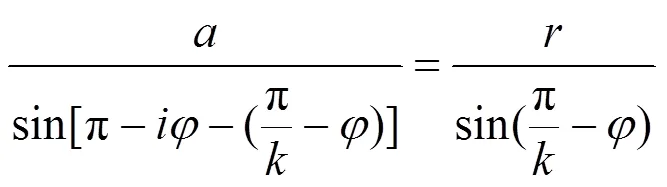
由于式(7)同时存在的加工边数和转速比之间存在联系,根据传动关系可知,当刀具轴上均匀装夹了把车刀,刀具轴与工件轴的转速比为(为整数)时,所形成的轴截面边数=×,故当刀具轴上只装夹一把车刀时,截面边数和转速比在数值上相等,化简式(7)可得:

联立式(6)(8)可以得到:
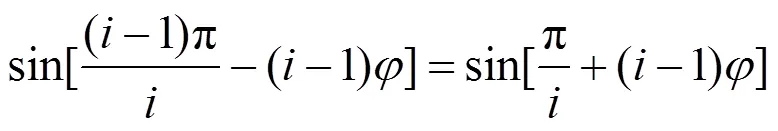
求解可得:
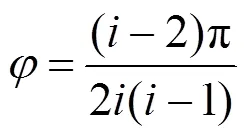
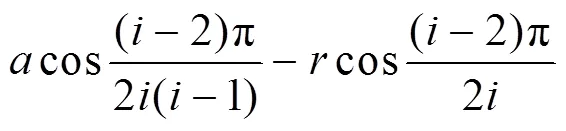

由式(10)可知:正多边形截面的误差由两轴中心距、刀具回转半径、转速比共同决定;两轴中心距与误差呈正相关,两轴中心距越大、则误差越大;而刀具回转半径与误差呈负相关,刀具回转半径越小、形成的曲面越凹、自然平面度误差也就越大[9];而由于本方案只采用一把车刀加工,所以转速比由实际的加工生产方案中的加工边数来决定,代入生产中常用的加工边数,即可获得对应的两轴中心距和刀具回转半径的代数关系如下:
加工正三角形截面轴时,=3,则有:

加工正方形截面轴时,=4,则有:
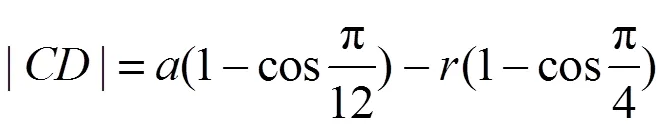
加工正五边形截面轴时,=5,则有:

加工正六边形截面轴时,=6,则有:
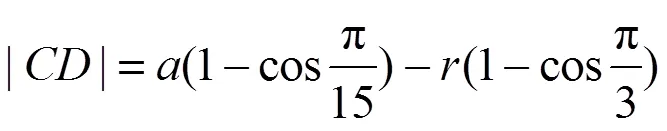
式(12)~(15)即为加工边数不同时所形成的不同误差与两轴中心距和刀具回转半径的关系式,在实际加工中可以通过调整两轴中心距和刀具回转半径来控制误差的大小。
而在前文中的MATLAB仿真分析轨迹时提到过,截面的凹凸程度与两轴中心距及刀具回转半径的比值有关,即当两轴中心距和刀具回转半径的比值发生变化时,成型截面的误差也会发生变化,下面将对其进行分析。
在理想情况下,加工得到的截面形状恰好是正多边形,即此时的||为零,但由于加工中的各项因素,导致加工误差必定是存在的,如果将加工误差近似地看作为零,即可得到相应的关系式如下:
加工正三角形截面轴时,令||≥0,则有:
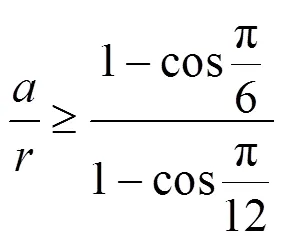
加工正方形截面轴时,令||≥0,则有:

加工正五边形截面轴时,令||≥0,则有:
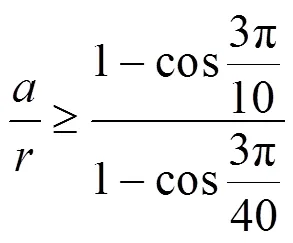
加工正六边形截面轴时,令||≥0,则有:
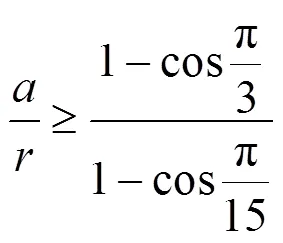
这样就得到了将误差近似看作0时初步得到的两轴中心距和刀具回转半径的比值,其他情况都是理想条件下时,尽量满足对应边数的比值,得到的误差会是一个比较满意的结果。在实际生产中,车间可根据这样的比值,结合加工零件的实际尺寸来调整两轴中心距及刀具回转半径,进而减小加工误差,提高加工精度。
3.2 多边形截面直线度误差验算
前文得出了加工时为了得到较好的直线度误差所需要满足的中心距与回转半径的比值关系,由于其关系式内存在余弦函数,故其比值为无限不循环小数,取临界值的本质是向临界无限靠近,所以小数点后的位数取得越多,截面的直线度误差就越小。
下面将以正六边形截面为例说明,验算该关系能否使直线度误差达到0.025 μm。
正六边形截面直线度误差为||=(1-cos(π/15))-(1-cos(π/3)),中心距与回转半径的比值为(1-cos(π/3))/(1-cos(π/15)),将余弦值小数点位数取到后六位时,比值为22.8812,回转半径同样取10 mm、12.5 mm、15 mm及20 mm,直线度误差如表1所示,可得当余弦值取到小数点后六位时,获得的直线度误差符合≤0.025 μm的要求,即在实际加工中,保持这一比值来对中心距与回转半径进行调整,就能加工出符合直线度要求的截面。而在实际加工中,当刀具的主偏角和副偏角为零时,通过刀具沿工件轴线水平移动即可将轴截面的直线度转化为整根轴的平面度,从而可得到轴上多边形平面度误差≤0.025 μm[10]。
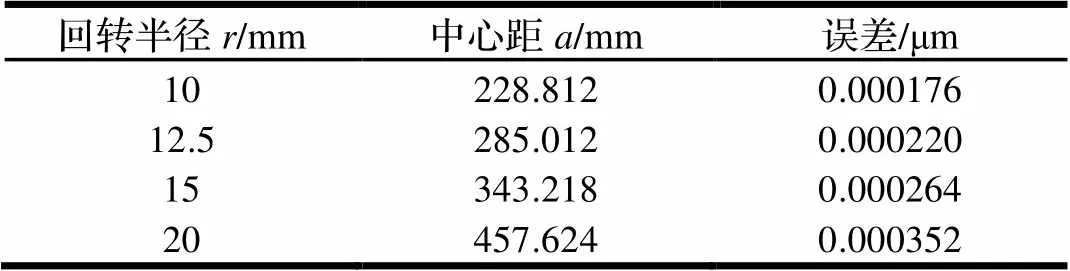
表1 中心距与回转半径比值为22.8812时的直线度误差
4 MATLAB仿真检验
前文得出了中心距和回转半径的比值,满足直线度误差不超过0.025 μm得到加工截面边数和对应的比值如表2所示。

表2 截面边数与对应的比值
仍以三角形与六边形截面为例,运用MATLAB软件对表2陈列的比值结果进行仿真检验,如图6所示,可以看出,截面的曲边得到了较好的修整,且原本容易产生应力集中的尖角也被转化为圆角,在一定程度上有助于提高轴的使用寿命[11]。
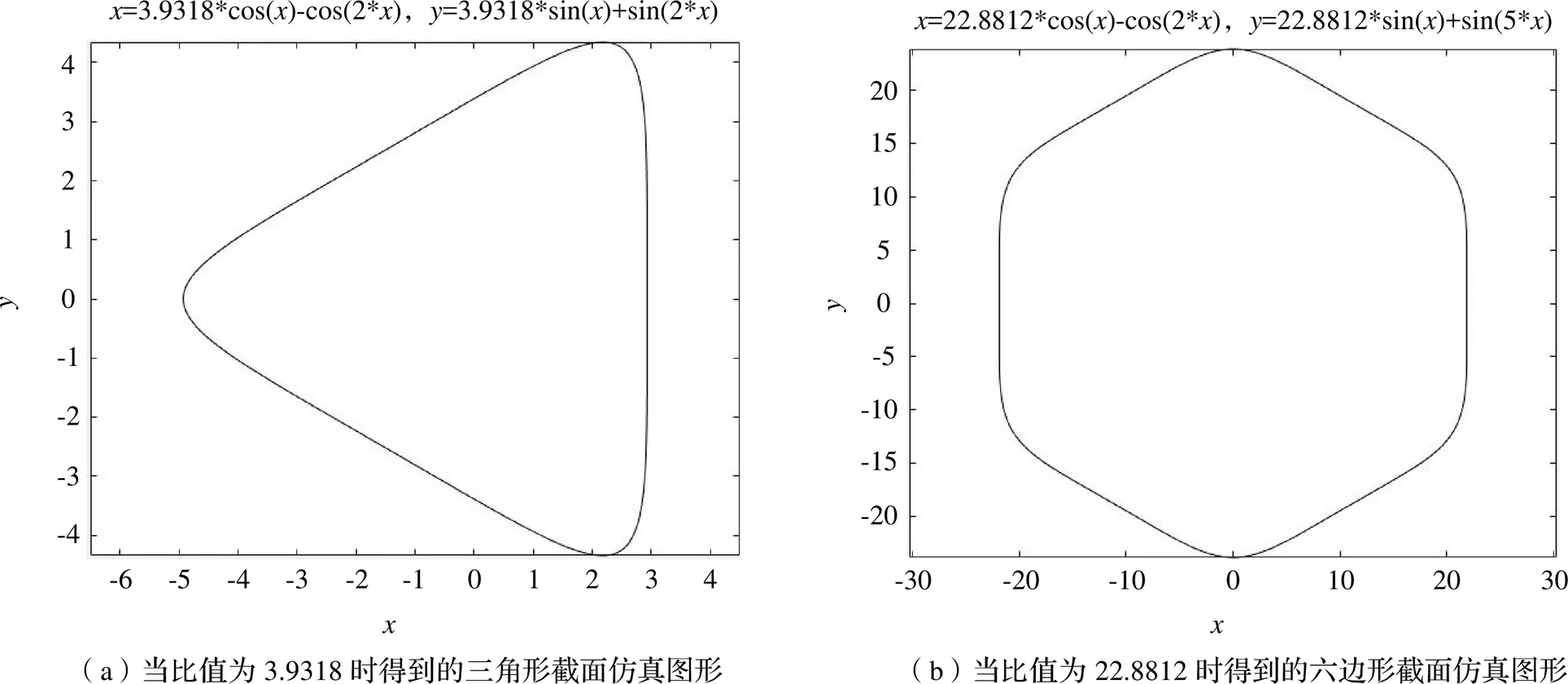
图6 成特定比例的不同截面仿真图形
5 结论
本文从对多边形截面轴的成型原理入手,对该类轴的误差进行了来源分析及优化计算,得出了如下结论:
(1)电子齿轮传动方案在大部分场合下具有比机械齿轮传动方案更大的选择范围、更高的加工效率及加工精度。
(2)两轴间的中心距和刀具的回转半径比值是影响截面内摆线轨迹曲边直线度误差的主要因素,当两者比值发生改变后,内摆线轨迹直线度误差发生变化。
(3)对于不同边数的截面而言,当中心距和回转半径成一定比例时,内摆线轨迹的曲边直线度误差能够得到优化。
[1]赵韩,徐林森,吴焱明,等. 固定轮系的旋轮线及在车削多面体中的应用[J]. 农业机械学报,2006(11):125-128.
[2]赵韩,徐林森,吴焱明,等. 车削多面体运动的矢量建模及误差分析[J]. 农业机械学报,2007(4):154-157.
[3]葛秀光,李佳,王丽萍,等. 摆线在多边形零件加工中的应用[J]. 机床与液压,2005(2):45-47.
[4]Sung L. M.,Tsai Y. C.. A study on the mathematical models and contact ratios of extended cycloid and cycloid bevel gear sets[J]. Mechanism and Machine Theory,1997,32(1):39-50.
[5]汪诤. 内摆线原理和车方机床分析[J]. 兰州交通大学学报,2010,29(4):119-121.
[6]韩绍民,赵庆志,刘世忠,等. 数控机床电子齿轮传动比计算方法及其机械性能研究[J]. 装备制造技术,2014(3):34-36.
[7]王义朋. 数控车方机床的加工和发展趋势研究[J]. 现代制造技术与装备,2018(6):159-160.
[8]胡昌军,钱瑞明,冯淑慧. 回转车床上的正多面体零件加工及误差分析[J]. 轻工机械,2008,26(6):4.
[9]扈传云,吴亚瑾. 端部为正多边形的轴类零件的加工[J]. 机械工程师,2001(7):42.
[10]邓中亮.非圆零件车削加工技术[M]. 1版. 北京:人民邮电出版社,1998.
[11]《机械设计手册》联合编写组. 机械设计手册[M]. 北京:化学工业出版社,1982.
Working Principle and Error Analysis of CNC Lathe for Polygonal Shaft Parts Based on Electronic Transmission Ratio
NI Mingwei,LUO Hongbo
( School of Mechanical Engineering,Sichuan University, Chengdu 610065, China )
Polygonal shaft parts have the characteristics of keyless connection and are widely used in many transmission scenarios, but the traditional machining methods have the disadvantages of low accuracy and low efficiency. In recent years, a method of turning polygon axes with two axes turning in the same direction has been proposed. This paper aims to reduce the flatness error of turning polygon axes on CNC lathes. Based on the molding principle of polygon axis, the geometric model of the tool tip trajectory was established and the trajectory equation of the tool tip was analyzed. The simulation trajectory of the polygon axis section with different number of edges was obtained by substituting the trajectory equation of the tool tip into MATLAB. After geometric analysis of the simulation trajectory, the expression of the section straightness error is obtained, that is, the machining error can be obtained by adjusting the machining parameters in the actual machining. According to the above methods, the machining parameters required by different edge shapes to meet the flatness error (not more than 0.025 μm) of the project were finally obtained.
electronic transmission ratio;polygon axis;error analysis;the MATLAB simulation
TH16;TH114
A
10.3969/j.issn.1006-0316.2022.10.002
1006-0316 (2022) 10-0008-07
2021-03-24
四川省科技计划重点研发项目(2021YFG0188);2017-2018四川省科技厅重点研发项目“基于电子传动比的多边形轴类零件复合数控车床”(2021YFG0188)
倪明威(1999-),四川成都人,主要研究方向为机械制造,E-mail:1284607302@qq.com;罗红波(1963-),四川成都人,工学硕士,副教授、硕士生导师,主要研究方向为数控机床、机械结构设计,E-mail:lhuuo630@126.com。
