基于区间映射和最大扰动区域的矢量地图可逆水印算法
2022-11-29张新长
奚 旭,张新长
1. 苏州科技大学地理科学与测绘工程学院,江苏 苏州 215009; 2. 广州大学地理科学与遥感学院,广东 广州 510006
矢量地图具有极高的社会经济价值,在数字经济、智慧城市、虚拟现实等新兴发展理念中具有重要基础功能[1-3]。在当前大数据时代,矢量地图的非法传播、倒卖与篡改等行为越来越猖狂,给数据合法拥有方造成了难以估量的损失[4-5]。数字水印[6-7]作为信息安全领域的前沿技术被引用到矢量地图中,为地理空间数据的版权保护提供了技术支持。
目前,矢量地图水印的研究成果已经非常丰富,根据传统的嵌入方式主要分为空间域水印算法和频率域水印算法[5,8],这两种算法通过直接或间接修改坐标值的方式实现水印嵌入。由于水印信息的嵌入会对坐标点造成扰动,因此,在设计水印方案的同时设计数据质量控制措施是矢量地图数字水印研究领域的一个重要方向[9]。文献[10]用相对位置精度和绝对位置精度作为约束条件,在线要素的周长和面要素的面积中嵌入水印,确保坐标点的变化在允许容差范围内。文献[11]利用多边形相似变换,基于量化索引调制的方法,将水印信息调制于多边形要素的空间关系的特征集合中,有效保持了要素的几何形状。文献[12]将水印嵌入至扩大倍数离散傅里叶变换的(discrete Fourier transform,DFT)相位和幅度上,在一定程度上减少了数据扰动等。以上研究均设计了质量控制方法,但仍然会在不同程度上降低数据保真度,因此,具有无损性质的水印算法越来越受关注。
可逆水印[13]算法在正确提取水印的同时可以恢复原始数据,保证数据质量不受影响,具有无损特性,是矢量地图数字水印研究的一个热点方向[14-16]。文献[17]基于离散余弦变换(discrete cosine transform,DCT)设计了矢量地图的可逆水印算法,这是可逆水印首次在矢量地图中的应用,但该方法是基于频率域变换实现的水印嵌入,在水印容量、可逆性及不可见性方面的表现都存在不足。为了提升可逆水印算法在矢量地图中的应用能力,国内外学者在提升算法性能方面做出了很多工作。文献[18—19]分别设计了基于差值扩张的矢量地图可逆水印算法,通过修改相邻顶点间的距离值实现水印嵌入,这类方法在水印容量方面表现出较好的性能,但嵌入水印时未考虑要素的几何特征,导致存在较多的要素形态扭曲情况。文献[20]对差值扩张算法进行了改进,通过修改顶点坐标与线要素的重心坐标的差值实现水印的嵌入,在提升水印容量方面效果显著,但数据的扰动情况并未得到改善。文献[21]以单个要素中特征点集的平均坐标为水印嵌入域,设计了一种可迭代嵌入的矢量地图可逆水印方案,该方法显著提升了水印容量,但迭代嵌入对要素的扰动情况介绍较少。文献[22—24]将地理坐标转换为极坐标,以极坐标为嵌入域设计了多种矢量地图可逆水印算法,并以QR码为水印信息载体,通过提升荷载能力的方式实现了水印信息的大容量嵌入,且采用QR码可减少对数据的扰动,但在不可见性的定量控制方面仍关注较少。综上所述,提升水印容量是矢量地图可逆水印算法研究的一个热点方向,水印容量的提升可以增大可逆水印的恢复提取概率,但也意味着载体数据需要牺牲更多的数据精度来提供水印嵌入空间。虽然可逆水印算法可以在提取水印后实现数据恢复,但过度扰动不仅会影响数据的可用性,也可能会暴露水印信息的存在,从而降低算法的安全性。因此,关注可逆算法下数据的扰动问题,设计科学合理的定量化可控扰动措施,对于提升矢量地图可逆水印算法的实用性具有重要意义。
针对上述问题,本文通过建立坐标点的状态区间轴,以量化索引调制的思想调制坐标点的状态值,将水印信息映射到状态区间中,状态区间根据矢量地图中坐标点的最大扰动区域(maximum perturbation region,MPR)进行范围限制,从而控制坐标点的合理移动范围,实现扰动程度可控的矢量地图可逆水印算法。
1 可控扰动的区间映射可逆水印算法
1.1 数据预处理方法
1.1.1 矢量地图预处理
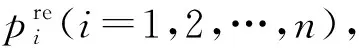
1.1.2 水印信息预处理


(1)
在嵌入水印时,将Wdecimal中的nw个水印序列按照设定的顺序嵌入nw个坐标值中。

(2)
1.2 水印嵌入方法
水印嵌入的基本思路如下:①建立一个可包含所有特征点的状态坐标轴,并将特征点按横坐标的值置于轴内;②设定合适区间等分状态坐标轴,使各个点在状态区间内;③继续将状态区间等分,得到状态值子区间;④利用水印信息依次调制重排序后的特征点的状态值,实现水印嵌入。
对区间的状态值(也称为序列号)作如下定义:假设xleft、x和xright(xleft≤x≤xright)是基于x轴排序序列中的3个坐标,将xleft和xright之间的区间等分为m(m≥2)个子区间,那么x坐标所在位置的子区间序列号就是区间状态值s。图1中所示x的区间状态值为3。

图1 m个等分区间时x的区间状态值Fig.1 The interval state value of x at m equal intervals
定义Q为包含xleft、x和xright所在的区间,即Q=(xleft,x,xright);xcenter为区间Q的中点,即xcenter=(xleft+xright)/2。设区间个数m=2c+1,则Q被等分为2c+1个子区间,如图2所示。

图2 x在Q中的区间状态值Fig.2 The interval state value of x in Q
定义w为x需要携带的水印,其中0≤w≤2c。x在嵌入水印后,其数值将映射到水印w所在的区间,因为0≤w≤2c,所以x的数值依然会在区间[xleft,xright)中。区间Q内的任意位置的x通过这种映射方法都不会超过Q的范围。
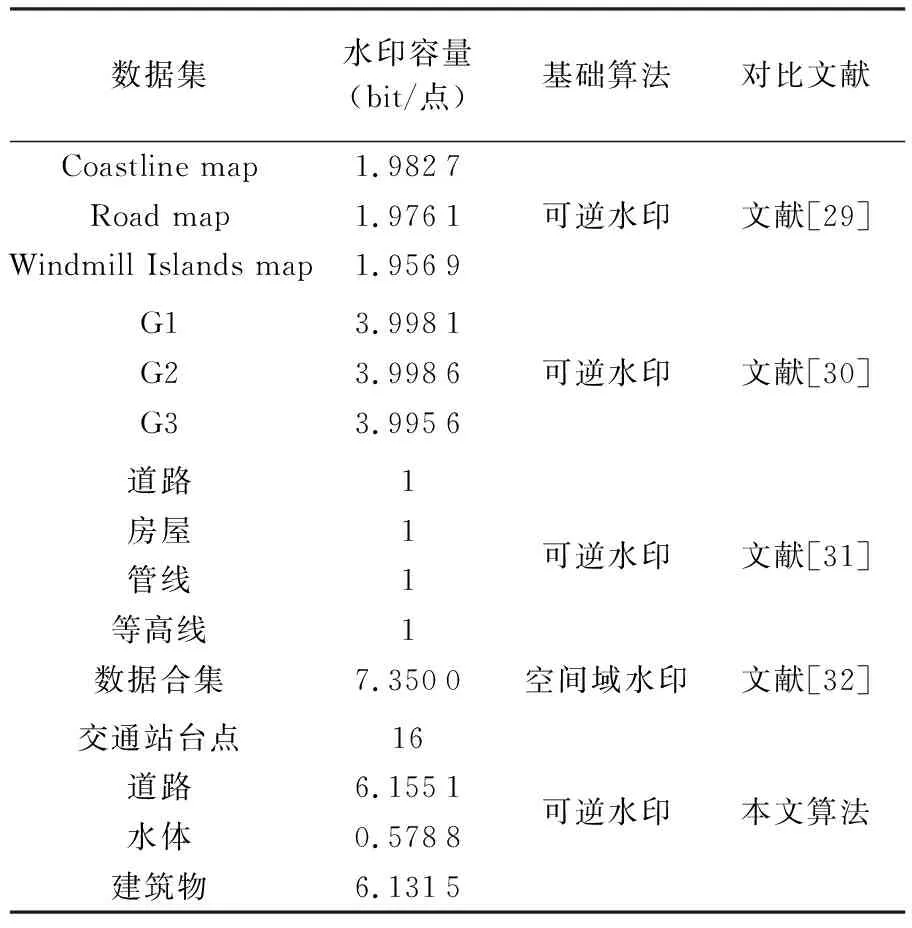
定义r为x位于区间Q中的系数,当x 图3 r值的设定规则Fig.3 The setting rule of r 在水印嵌入过程中,需要嵌入水印的x在区间Q的系数r可以通过式(3)进行计算 (3) 将x进行水印嵌入后的值记为x′,x′在Q中的区间状态值记为s′,s′也就是x′应该落在Q中的子区间的序号,其计算公式为 s′=2c×r+w (4) 因为w取值范围为0≤w≤2c,由式(3)可知,r的取值为0或1,所以s′的取值范围为0≤s′<2c+1,x′也不会超过Q的范围。通过式(5)移动x到第s′个区间 (5) (6) 定义区间Q的子区间的等间距ls为 (7) 图4 x经过区间映射嵌入水印Fig.4 The watermark embedded in x through interval mapping 通过对x区间状态值的映射可以实现水印的嵌入,如果区间Q不变,可以提取出x′的区间状态值,然后通过算法可以恢复原始的x。 在水印的提取阶段,x′在Q的区间状态值s′,可以通过x′与Q的子区间间隔ls求出 s′=[(x′-xleft)/ls] (8) 将式(8)转换为 s′=[(x′-xleft)/(xright-xleft)/2c+1] (9) 则水印x′携带的水印值w可以通过式(10)被提取出来 w=s′-r×2c (10) 最后,原始x可以通过式(11)进行恢复 (11) 在上述算法的实现过程中,坐标的区间状态值与水印的信息位进行了一一映射,坐标点所在的区间位置也记录了对应水印信息的索引信息,在数学原理上不仅能够对坐标进行水印嵌入,而且可以精确地提取出水印并恢复数据。 Ri=Dvi(ri) (12) 图5 基于Delaunay三角网的最大扰动区域计算方法Fig.5 The maximum perturbation region was calculated based on Delaunay triangular mesh 计算得到所有坐标点的MPR后,取最小半径Rmin作为xleft和xright的差值,此时xleft=x-Rmin,xright=x+Rmin。为了在水印提取时能重构状态区间轴,在水印嵌入前,首先找到坐标轴中最值xmax和xmin,然后自定义设置坐标轴大区间Lx的最小值和最大值,要求Xmin≤xmin、Xmax≥xmax。本文采用图层空间域的最值作为Xmin和Xmax,可实现全盲检测。提取时,只需要输入Xmin和Xmax作为密钥重构新的坐标轴即可。定义LX(Xmin,X,Xmax)为包含Xmin、X和Xmax的区间,将区间LX等分为Dx(Dx≥2)个子区间,每个子区间的长度为2Rmin,则有 2Rmin=(Xmax-Xmin)/Dx (13) λxi=[(xi-Xmin)/2Rmin] (14) (15) 图6为整个X坐标区间及x的虚拟坐标。 图6 虚拟坐标Fig.6 Virtual coordinates 基于区间映射与MPR扰动控制的矢量地图可逆水印算法嵌入流程如图7所示,具体步骤如下。 (1) 数据预处理:对原始矢量地图G,采用Douglas-Peucker算法,设置阈值τ,提取特征点pi;计算各特征点至地图几何中心的距离di,按距离值大小重排序;将二值水印图像I进行Arnold置乱,选择置乱加密的图像IA读取为二进制流水印信息Wbinary,并转换为十进制数Wdecimal。 (2) 构建区间状态轴:根据图层域的最值Xmin和Xmax建立一个可包含所有特征点x坐标的坐标轴LX,并将特征点集按坐标值大小置于LX中的相应位置,得到区间状态轴。 图7 水印嵌入流程Fig.7 Flowchart of watermark embedding (3) 获取区间状态值:根据原始矢量地图计算所有坐标点的MPR,取最小MPR的直径2Rmin作为区间状态轴的区间范围Q;利用水印位c继续将区间Q划分为2c+1个子区间,根据特征点所处的子区间位置获取每个特征点的区间状态值s。 (5) 将含水印特征点与非特征点一起写入文件,得到含水印矢量地图G′。 水印提取是水印嵌入的逆过程,基本步骤如下。 (2) 水印提取与数据恢复:根据1.2节提出的水印算法进行水印信息提取并同时恢复坐标值,对提取出的十进制水印数组(Wdecimal)′进行二进制流转换,并读取为二进制图像(IA)′;通过Arnold逆置乱,恢复得到水印图像I′。 (3) 水印检测:将提取到的多个水印图像I′与原始水印图像I进行对比验证,用归一化相关系数(normalized correlation,NC)衡量图像之间的相似性[27],具体公式如下 (16) (17) 式中,L为水印信息的长度。水印容量是衡量被保护数据含有水印信息量大小的主要指标,矢量地图的基本计量为顶点,因此水印容量指标定义为 (18) 在水印提取时,要对密钥进行解析,按照顺序对嵌入的水印点进行空间查找,从而提取出水印信息。一旦水印点被删除,查找不到,采用空值占位,也不会影响后续顶点的顺序。 2.1.1 原始矢量地图 本文选取涵盖点、线、面3种类型的矢量地图作为试验数据,如图8所示,分别为交通站台点、道路、水体及建筑物轮廓图。表1统计了预处理之后各个数据的基本信息,其中线、面数据的压缩阈值设置为2 m,点数据不进行压缩简化。通过计算,得到各个数据的MPR半径,确定了各数据的坐标点活动范围。可以看出,点密度越大的数据,其MPR范围越小,嵌入水印时可扰动的空间也越小。 图8 原始矢量地图Fig.8 Original vector maps 表1 原始矢量地图的数据信息 2.1.2 水印信息 试验嵌入的水印信息是一张大小为64×64像素的二值图像(图9(a)),图像内含有版权信息“地测学院”。为了提升安全性,采用Arnold算法[28]对其进行加密,在Arnold公式中所有参数取1的情况下(Arnold算法的公式参考文献[28]),得到本文水印图像的置乱周期为48次。图9展示了水印图像在置乱10次、20次、30次及48次时的结果,其中第10次、20次和30次置乱的水印图像为难以识别的噪声图,具有较好的隐蔽性,在第48次置乱时恢复成原始状态。本文选择第20次置乱的图像作为加密态的水印信息用于水印嵌入与提取。 图9 水印图像Fig.9 Watermark images 通过对二进制流水印信息的转化,得到c的最大可取数值为38,即每个坐标值最多可携带38 bit的水印码。为了防止水印嵌入后的坐标值在保存时被数据格式精度约减,产生较大误差,一般取较小值。综合考虑shape数据的存储特征及可嵌入量,将c值设置为8,即每个坐标值可携带8 bit信息。在可逆水印算法中,水印容量越大,提取出完整水印信息的概率越大。表2对比了近几年较热的大容量水印算法以及本文算法下的水印容量。在本文算法中,交通站点数据为非压缩情况下的有效水印嵌入量,可达到16 bit/点;水体数据中仅为0.578 8 bit/点,主要是因为水体数据的点密度很大,压缩后得到的特征点数量很少,因此水印容量明显小于其他数据。通过对比分析,本文算法在水印容量方面几乎仅次于文献[32],在有效水印嵌入量方面更是达到了16 bit/点,水印容量性能突出,本文算法的大容量特点主要得益于水印信息的十进制化操作以及坐标点状态值位置调制的包容性。 表2 水印容量对比 从拓扑质量、视觉观测和误差分析这3个方面进行水印不可见性分析。对含水印矢量地图拓扑检查发现不存在要素重叠及容差错误,因此水印嵌入未导致拓扑变更,图形质量得到较好维持。图10展示了道路图在水印嵌入前、后的对比情况, 在不放大的情况几乎难以察觉坐标点发生了偏移,放大后可见坐标点发生了细微改变,但要素的形状不存在明显的形变,要素的几何特征维持良好。表3统计了水印嵌入后与原始数据的误差值,在所有数据中,最大的误差改变量为0.000 851 32 m。根据国标《1∶500 1∶1000 1∶2000外业数字测图技术规程 GB14912—2005》中的地形图精度平面误差要求,1∶500地形图的点位误差为±0.15 m、1∶1000地形图的点位误差为±0.30 m、1∶2000地形图的点位误差为±0.60 m,由此可见,水印嵌入对数据的扰动非常小,不会影响数据的可用性。 表3 水印嵌入后的精度误差统计 图10 矢量地图嵌入水印前、后的叠置对比Fig.10 Superposition comparison of watermarked vector map and original vector map 为了检验本文算法的稳健性,分别对含水印矢量地图进行几何攻击、坐标点攻击以及裁剪攻击等,并与相关的水印算法作对比分析。限于篇幅,以下试验均在道路数据上进行。 2.4.1 几何攻击 本次试验的几何攻击主要包括旋转、平移、缩放及简化攻击。表4的统计结果显示,本文算法以及对比算法在不同强度的旋转、平移及缩放下,都可以提取到完整的水印图像,具有良好的抗几何攻击能力。在这些攻击下,数据未发生扭曲,得到的最小MPR的半径与原始数据的Rmin是一致的,特征点与原始数据也一致,因此可获取完整水印信息。本文算法预设的压缩阈值为2 m,在简化攻击时,不超过2 m的压缩阈值时可得到完整水印图像,超过2 m时,随着特征点的减少,可获取的水印信息也不断减少;而对比算法中只要有简化攻击,就无法提取出完整水印图像,且随着压缩阈值的提升,甚至无法完成提取试验。 表4 几何攻击试验结果 2.4.2 坐标点攻击 坐标点攻击包括随机增点和随机删点,试验强度为原数据的10%~60%逐步递增。图11所示为本文算法与文献[21]算法和文献[22]算法在不同强度坐标点攻击下得到的水印图像BER的变化曲线。图11(a)中,随机增点攻击对本文算法和文献[21]算法没有任何影响,始终可以得到BER值为0的完整水印图像;图11(b)中,随着删点比例的逐步增加,3种算法下可得到的水印图像的BER值都越来越高,本文算法与文献[22]算法结果比较接近,即便在60%的删点比例下,仍可以得到BER值低于10%的水印图像,展现出良好的抗删点攻击能力。综上,本文算法在抗增点和删点攻击均展现出优越的性能,具有较强的抗坐标点攻击的能力。 图11 坐标点攻击下水印图像的BER变化曲线Fig.11 BER variation curves of the extracted watermark images under point attacks 2.4.3 裁剪攻击 表5统计了在不同裁剪比例及裁剪位置情况下,本文算法及对比算法可提取到的最优水印图像。本文算法中,含水印特征点被删除时,该点所带的水印信息自动以空值占位,因此提取的水印图像不存在噪点。3种算法都随着裁剪尺度的增加,可提取的水印图像质量越来越差,但都展现出较强的稳健性,在30%、40%及50%裁剪比例下均可以获取可识别的水印图像。本文算法因有空值占位,在同一裁剪比例下,得到的NC值与BER值要明显要好于对比算法的结果;但在60%的裁剪尺度下,得到的水印可识别度较差,难以有效验证版权,而文献[21—22]得到的结果虽也难以完成验证功能,但仍有一定辨识度。总体而言,本文算法对裁剪攻击具有良好的稳健性,在50%的裁剪尺度下仍可提取出可靠的水印图像,足以胜任常规使用。 表5 裁剪攻击试验结果 从理论以及数学的角度,本文算法是可以完美无损地恢复原始矢量地图的,但对恢复后的数据与原始数据对比发现,恢复后的数据与原始数据存在一些极小的误差。主要原因在于受限于部分数据的MPR半径过小及GIS软件的精度位存储长度的限制,可供运算的结果在存储时会在精度位上进行四舍五入的约简,从而导致恢复后的数据与初始数据有一些微小误差。误差结果见表6,可以看出,这些误差对数据质量的影响很小,且仅限于数量不多的特征点,因此,本文算法具有较好的可逆性。 表6 数据恢复后与原始数据的误差统计 本文基于量化索引调制的思想设计了一种矢量地图区间映射的可逆水印算法,利用水印信息位调制坐标点的区间状态值的方式嵌入水印信息,通过区间位与水印信息位的一一映射实现水印信息的可逆提取与盲检测。在水印嵌入阶段,将二值水印信息进行十进制转化,并用于坐标区间状态值的调制,利用十进制数相较二进制数更强的信息承载能力实现水印的大容量嵌入;坐标的区间状态值范围采用最大扰动区域方法进行限制,将坐标扰动控制在合理范围内,从而控制了水印的隐蔽性。结合特征点提取,基于空间特征重排序等数据预处理,本文提出的可逆水印算法对常规几何攻击、坐标点攻击以及裁剪攻击等具有较强的稳健性,能较好地平衡水印方案的容量、不可见性及稳健性之间的相互制约关系。



1.3 基于MPR的扰动控制



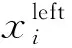
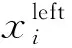
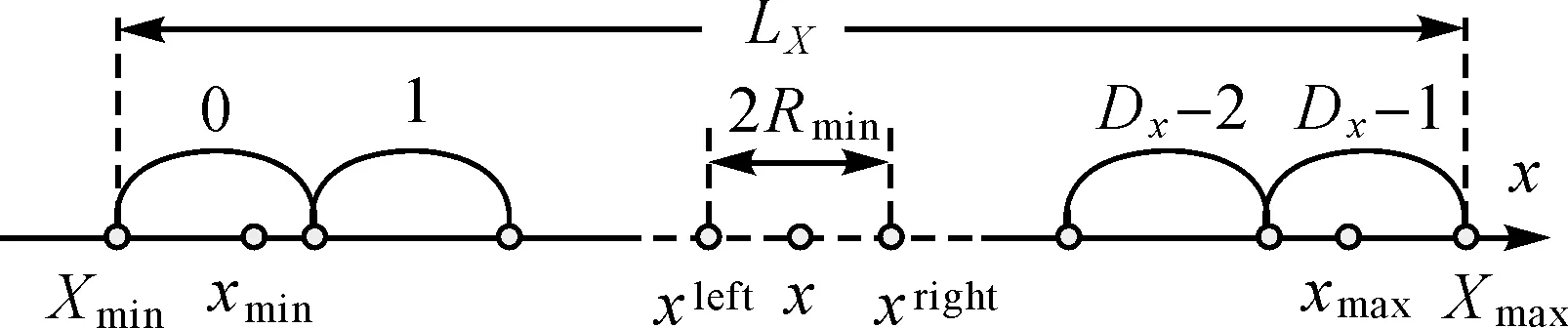

1.4 水印嵌入流程

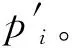
1.5 水印提取与检测


2 试验与分析
2.1 试验数据处理



2.2 水印容量分析
2.3 不可见性分析


2.4 稳健性分析



2.5 可逆性分析

3 结 论
