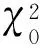GNSS模糊度解算的附加缩放因子的CLAMBDA方法
2022-11-29卢立果马立烨刘万科吴汤婷胡伟建
卢立果,马立烨,刘万科,吴汤婷,胡伟建
1. 东华理工大学测绘工程学院, 江西 南昌 330013; 2. 广西空间信息与测绘重点实验室(桂林理工大学),广西 桂林 541006; 3. 武汉大学卫星导航定位技术研究中心,湖北 武汉 430079; 4. 武汉大学测绘学院,湖北 武汉 430079
在一些GNSS定位场景下(比如姿态测量),GNSS天线之间的基线长度可以事先精确量取,常被用作先验信息参与基线处理和模糊度解算,以提高模糊度解算的成功率,称为附有基线长度约束的模糊度解算[1-2]。根据基线长信息的使用方式不同,主要分为3种方法:第一种是将基线长信息作为虚拟观测值,同伪距和相位观测值一起进行模糊度浮点解估计[3-5];第二种是将基线长信息用于模糊度整数值确认环节[6-8];第三种是基线二次型约束的整数最小二乘法(quadratically constrained integer least-squares,QC-ILS),它将基线长信息加入模糊度搜索及基线固定过程,通过扩大模糊度二次型的搜索范围,寻找满足混合二次型最小的模糊度向量[9-13]。由于QC-ILS解算是建立在标准LAMBDA(least-square ambiguity decorrelation adjustment)算法基础上,因此这种处理方法又称作约束LAMBDA算法(constrained LAMBDA,CLAMBDA)[10]。相较于其他两类方法,CLAMBDA可以严格地把基线长信息融合到整数最小二乘(integer least-squares,ILS)准则下[11]。针对弱GNSS模型,仅选取基线长信息参与模糊度解算,CLAMBDA可以显著提高模糊度解算成功率[12-16]。
尽管CLAMBDA具有优异的模糊度解算性能,但能否快速解算出模糊度是决定其具有实时应用的关键。文献[13]采用基于边界函数收缩的方法获得静态约7 ms、动态约20 ms的计算结果。文献[17]采用静态模拟数据获得约22 ms的计算结果。为更好地满足实时应用需求,文献[2]指出CLAMBDA在搜索方面仍有待进一步提高。而提高CLAMBDA解算效率的关键,首先在于如何设置合理的初始空间,其次在于如何更好地更新搜索空间。在CLAMBDA解算时,为保障初始搜索空间包含CLAMBDA解,通常设置一个非空的初始搜索空间(即至少包含一组模糊度候选向量)[13]。针对弱GNSS模型模糊度解算成功率较低,采用ILS等整数估计方法获得的初始模糊度向量将严重偏离真值[10],从而导致计算的初始搜索空间过大,难以快速获取CLAMBDA解。
因此,为进一步提高CLAMDBA的解算效率,本文将重点针对初始搜索空间的设置和更新开展相关研究。
1 CLAMBDA解算模型
加入基线长约束后的GNSS数学模型为[10]
(1)
式中,y为GNSS观测值;l为量取的基线长;a和b分别为模糊度和基线分量参数;A和B为相应的系数矩阵;E(·)和D(·)分别表示期望和方差算子。
对式(1)采用最小二乘估计,并进行正交分解
(2)
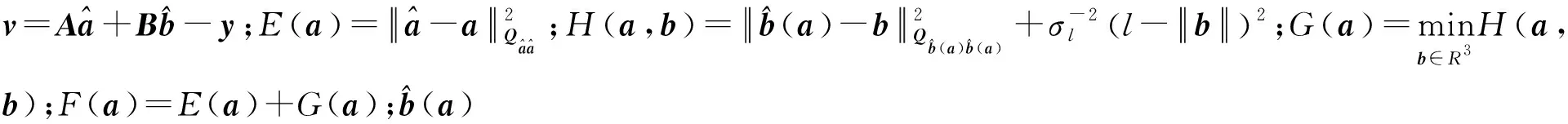
F(a)=min
(3)
式(3)通过约束条件,把模糊度ILS解算问题转化成QC-ILS问题。由于满足E(a)最小的模糊度不一定满足F(a)最小,即模糊度搜索空间不再为椭球体。当解算出各个整数模糊度a及其对应的b(a)后求取F(a),选择满足F(a)最小的a和b(a)作为最终固定的整数模糊度向量和基线分量。
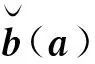
(4)
(5)
2 CLAMBDA快速搜索算法
2.1 边界函数法
为实现CLAMBDA的快速解算,目前性能最优的方法是基于边界函数进行搜索空间收缩的算法(bounding functions search and shrink strategy,BFS)[2,12]。
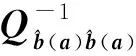
(6)
则F(a)存在下述不等关系
F1(a)≤F(a)≤F2(a)
(7)
式中
当搜索空间大小为χ2时,各自对应的模糊度候选整数向量空间为
(8)
式(8)表示在相同搜索空间内F1(a)包含的模糊度向量个数依次大于F(a)和F2(a),整数向量空间关系为
ΩF2(χ2)⊂ΩF(χ2)⊂ΩF1(χ2)
(9)

2.2 改进的搜索算法
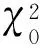
2.2.1 缩放因子定义
假令ASS的搜索空间大小为χ2,则满足如下关系式
(10)
式中,μ1为缩小因子,μ2为放大因子,为避免空间的放大和缩小过程陷入死循环,必须保证μ1×μ2≠1;i为模糊度向量个数统计指标,表示在搜索空间χ2内基于深度优先搜索算法枚举的候选模糊度向量个数[18-19];threshold为χ2内模糊度候选向量个数的阈值;k为收缩空间次数统计指标,表示F2(a)更新搜索空间的次数。μ1、μ2和threshold的具体设置下文将会进行详细讨论。
式(10)表示在搜索空间χ2中,枚举的候选向量个数超过阈值,说明当前搜索空间相对较大,则采用缩小因子降低χ2的数值;反之,如果在χ2内枚举出全部的候选整数向量个数没有超过阈值,但是所有整数向量的F2(a)值都大于χ2,未能更新搜索空间(k=0),说明搜索空间χ2相对过小,无法确认空间内包含满足二次型F(a)最小的模糊度最优解,则采用放大因子增大χ2的数值。
2.2.2 初始搜索空间设置
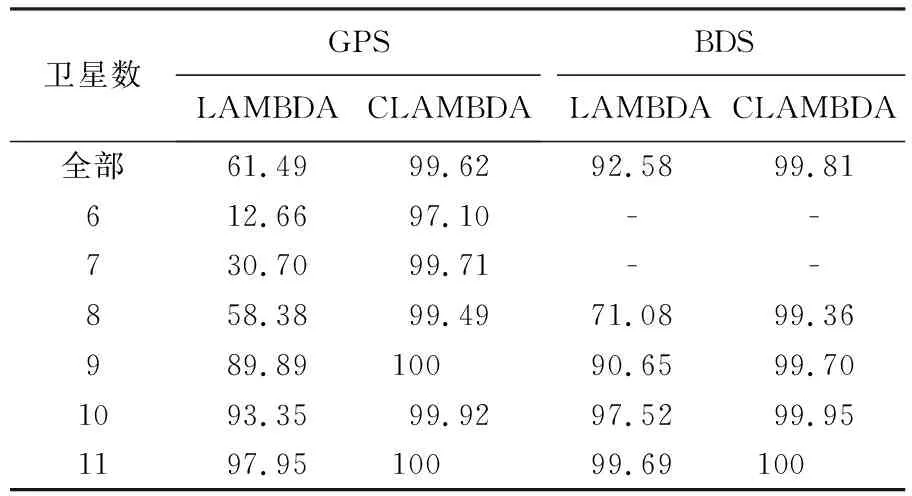
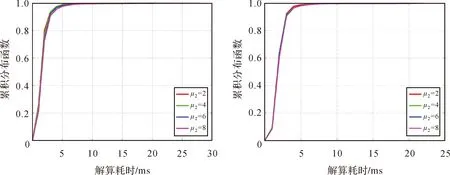
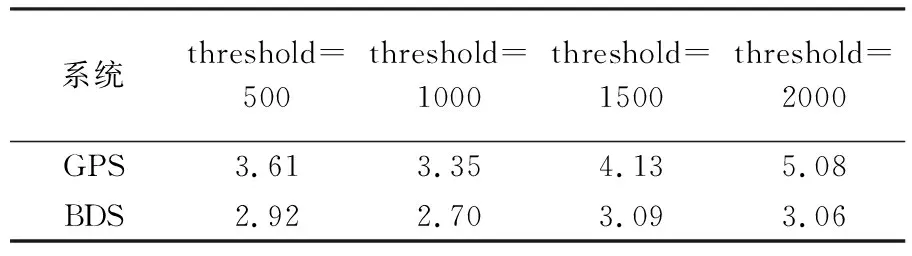
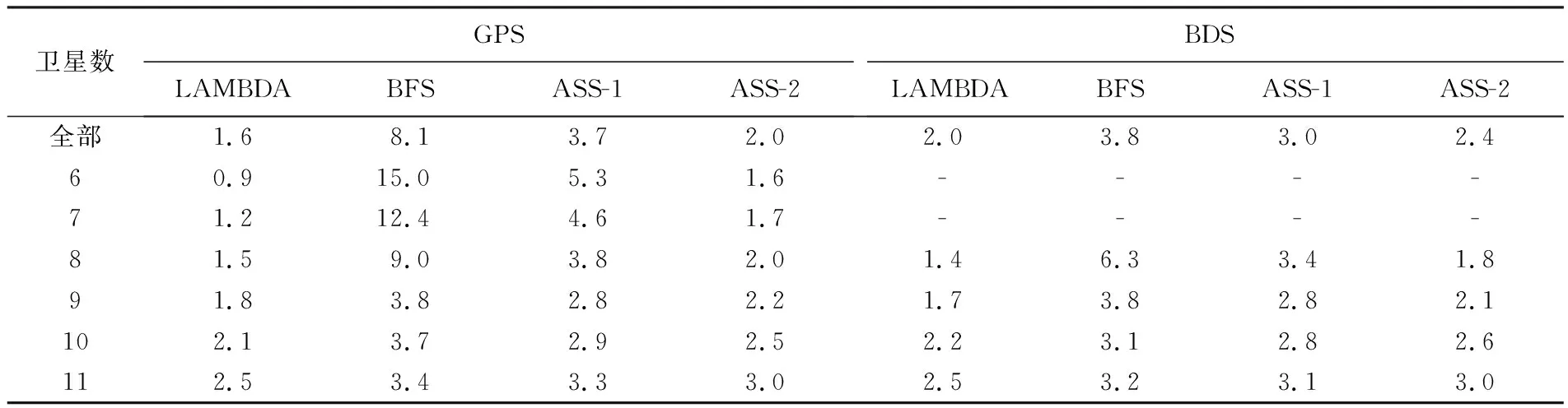
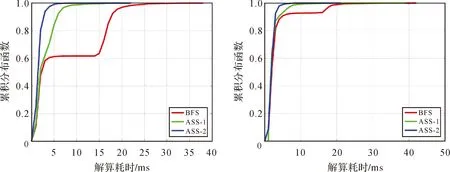
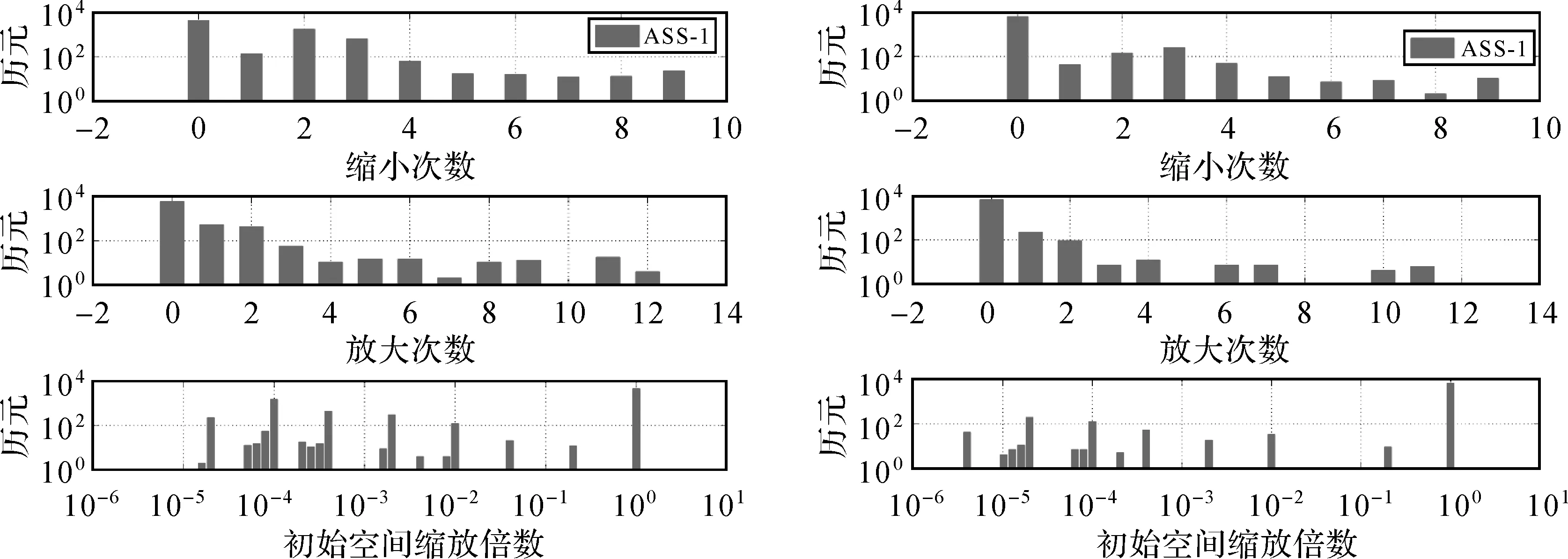
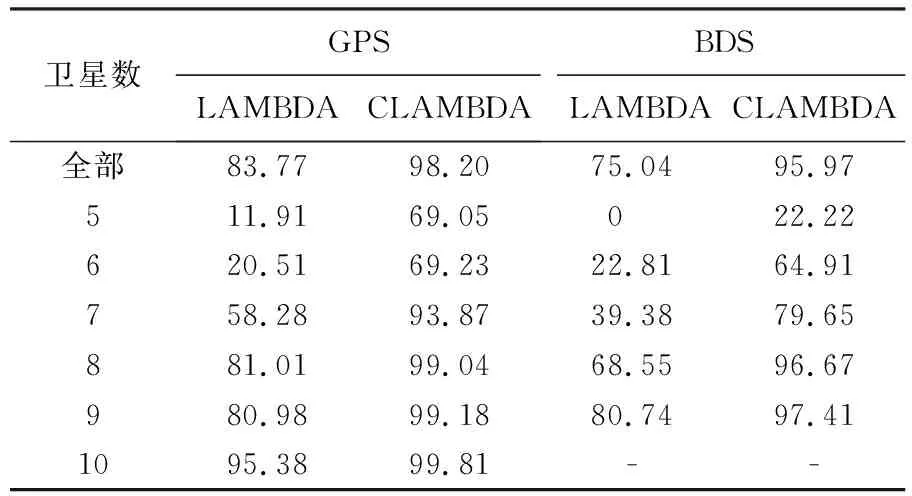
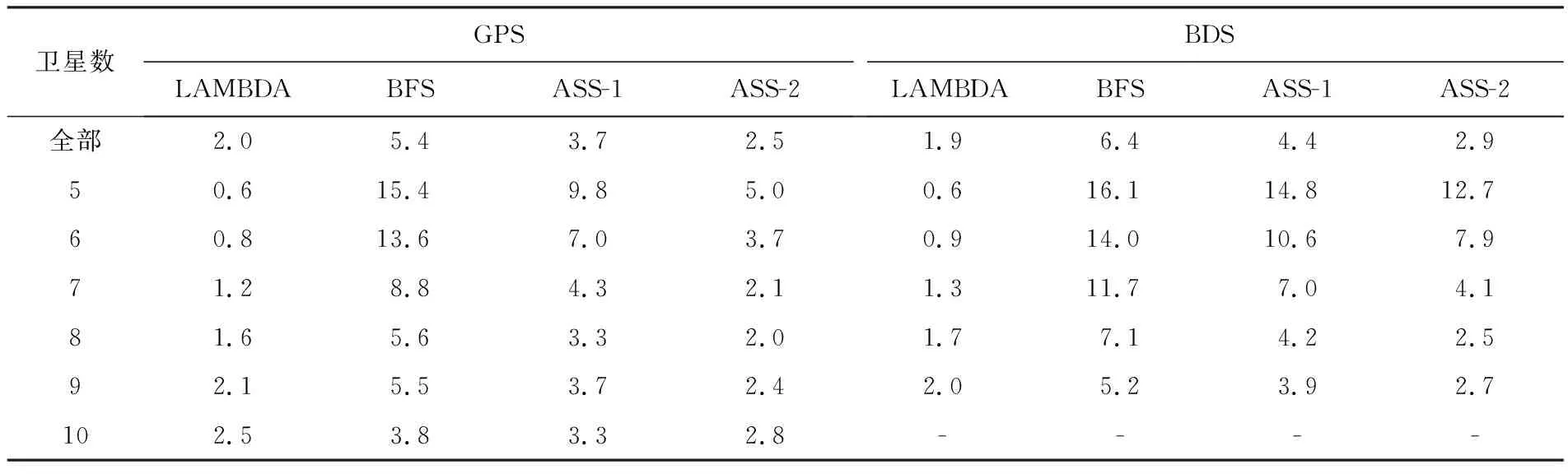
E0 (11) 2.2.3 实现流程 在BFS算法实现的基础上,基于缩放因子的ASS算法的具体步骤如下(图1): (2) 枚举出模糊度向量a,并计算对应的F2(a),更新i=i+1。 (7) 求取各个模糊度向量对应的F(a),选取满足F(a)最小的模糊度向量amin,此时amin即为CLAMBDA解。 图1 ASS搜索流程Fig.1 Flowchart of ASS search 为验证本文提出的基于缩放因子的ASS算法的搜索性能,采用LAMBDA算法和BFS算法(初始空间设置同ASS-1算法)来验证ASS算法的性能,并选取一组静态算例和一组动态车载算例进行试验对比分析,基本信息见表1。其中动态算例为GNSS测向试验,GNSS天线固连在刚性载体上,基线长度保持不变。为了纯粹地比较不同模糊度解算方法的效果,尽量不引入前后历元的观测信息,本文采用单历元模式进行模糊度解算,并使用NovAtel公司发布的高精度事后动态处理软件GrafMov计算结果作为参考真值,当基线3个方向分量(N、E、U)与参考真值的偏差小于3、3、6 cm,即认为模糊度固定正确;为提高CLAMBDA模糊度初值的准确率,加快模糊度的搜索效率,文中BFS算法和ASS算法均采用LAMBDA解作为初值来设置初始搜索空间。 本文的模糊度搜索耗时是在PC机上基于MATLAB 2016a软件进行统计的,其软硬件配置为:Intel Core i7-7700HQ CPU,2.80 GHz主频,8 GB内存,Win10操作系统(64位)。 表1 算例基本信息 该组数据采集于武汉某科技园楼顶,为静态超短基线观测数据。图2为共视卫星数和PDOP(position dilution of precision)值序列图,由图2可知GPS和BDS的可视卫星数均在10颗左右,PDOP值在3附近,观测条件良好。 图2 共视卫星数及PDOP值Fig.2 Number of common view satellites and PDOP value 3.1.1 模糊度固定成功率分析 表2统计了LAMBDA方法和CLAMBDA方法在基线长取不同先验精度σ下的模糊度固定成功率。其中,针对CLAMBDA解算的不同搜索算法仅影响搜索效率,而不影响最终的搜索结果,因此仅以ASS-2为例给出了CLAMBDA解算的模糊度固定成功率。由表2可知,采用LAMBDA方法进行模糊度固定时其固定成功率明显较低,采用CLAMBDA方法时, 由于加入了基线长信息,增强了模型强度,极大地提高了模糊度固定成功率,GPS和BDS的模糊度固定成功率普遍可提升至99%以上。另一方面,不同的σ也会对模糊度解算的成功率带来一定影响,在σ大于5 cm时,会影响CLAMBDA的解算性能,因此在实际使用时σ设置不宜过大,本文后续CLAMBDA的试验对比分析均采用σ=0的强约束模型[11,13]。 表2 不同先验信息下的模糊度固定成功率 表3统计了不同卫星个数下的模糊度成功率。由表3可以看出,LAMBDA算法固定成功率与卫星数呈正相关关系,受GNSS模型强度影响较大,而CLAMBDA方法在针对弱GNSS的观测场景,可以显著提高模糊度的固定成功率。 表3 不同卫星个数下的模糊度固定成功率 3.1.2 缩放因子和候选向量个数阈值设置分析 根据上节分析可知CLAMBDA针对弱GNSS模型具有较好的模糊度解算性能,下面将探讨如何实现CLAMBDA的快速解算。由于ASS-1和ASS-2两种算法初始空间设置不同,对缩放因子选取也不同,本节将对两种算法下的缩放因子和模糊度候选向量个数阈值如何设置进行讨论,为后续算法的具体实现提供依据。 图3 Fc与E0和F0的关系Fig.3 Relationship among Fc, E0 and F0 表4 不同缩小因子下ASS-1平均解算耗时 图4 不同缩小因子下ASS-1的解算耗时累积分布函数Fig.4 Cumulative distribution function of resolution time of ASS-1 under different reduction factors 表5 不同放大因子下ASS-2平均解算耗时 图5 不同放大因子下ASS-2的解算耗时累积分布函数Fig.5 Cumulative distribution function of resolution time of ASS-2 under different amplification factors 针对每个搜索空间χ2中阈值threshold的设置问题,首先作一简要分析,如果threshold设置过小,则会过于频繁地缩小搜索空间,模糊度搜索时需要不断地初始化,影响搜索效率;设置过大则不利于搜索空间的收缩,同样影响搜索效率。基于此,笔者设置threshold分别为500、1000、1500和2000,比较不同threshold下ASS-1算法的解算性能(当搜索空间收缩时,表明枚举的候选向量数大于threshold,由于ASS-1算法以收缩空间为主,threshold数值的设置对ASS-1算法影响较大,因此采用ASS-1算法进行分析)。表6为不同threshold下统计的ASS-1平均解算耗时,图6为对应的累积分布函数图。由图6和表6可知,在threshold为1000时,可获得较好的解算效果。因此,本文ASS算法的threshold设置为1000。 图6 不同阈值下的ASS-1解算耗时累积分布函数Fig.6 Cumulative distribution function of resolution time of ASS-1 under different thresholds 需要说明的是,上述缩放因子和阈值的参数设置是通过文中算例具体比较分析得出的,不能保证为最优参数值,但采用上述设置可以达到较好的解算效果,仍不失一般性。 表6 不同阈值下ASS-1平均解算耗时 3.1.3 解算耗时验证分析 通过上节详细的试验对比分析给出了ASS算法的具体参数设置,下面将具体验证ASS算法的解算性能。 表7统计了不同卫星数下的模糊度平均解算耗时。由表7可知,ASS-2算法平均解算耗时在2.5 ms以内,解算性能接近于LAMBDA算法,ASS-1次之,BFS最差;对于GPS数据,ASS-2整体解算效率相对于BFS能够提高3倍以上,对于BDS数据,ASS-2整体解算效率相对于BFS也能够提高58%以上;ASS-2解算耗时与卫星个数呈正相关,随着卫星数的增加解算耗时也随之增加;BFS解算耗时与卫星个数基本呈负相关,卫星数越少解算耗时越大;ASS-1解算耗时处于二者之间;在弱GNSS模型(如卫星数不超过8颗时)情形下,ASS-2解算效率显著优于BFS,但随着卫星观测个数的增加,GNSS模型强度的增强,3种算法均能实现快速搜索,解算性能差异也随之减小。 表7 不同卫星数下的模糊度平均解算耗时对比 图7为BFS、ASS-1和ASS-2这3种算法的解算耗时对比。由图可以直观看到三者的解算性能优劣,此处不再赘述;同时,图7中BFS趋势和图3中F0/Fc趋势基本一致,说明BFS解算效率与初始空间大小直接相关,即取决于GNSS模型强度。 图7 3种算法解算耗时对比Fig.7 Comparison of resolution time of three algorithms 根据BFS、ASS-1和ASS-2解算耗时比较,其解算效率存在如下关系:ASS-2>ASS-1>BFS。由于ASS-1相较于BFS增加了缩放因子,ASS-2相较于ASS-1采用的初始空间不同,为便于分析不同因素对ASS算法的影响,下面分别从ASS-1相对BFS的提高原因、ASS-2相对ASS-1的提高原因两个方面分别进行分析。 图8 ASS-1算法缩小和放大次数及初始空间变化Fig.8 Reduction and amplification times and initial space change of ASS-1 algorithm 其次,分析ASS-2解算效率高于ASS-1的原因。图9为ASS-1和ASS-2算法在缩放次数(放大次数+缩小次数)和解算耗时方面的比较关系图。由图9可知,ASS-2的缩放次数小于ASS-1,主要因为2E0相较于F0,与Fc差异较小,进行空间缩放时更易调整搜索空间;在解算耗时方面,ASS-2耗时小于ASS-1,且与缩放次数的变化趋势基本一致,主要因为每次完成缩放均需重新进行初始化搜索,缩放次数越多,搜索耗时越大,反之亦然。因此,ASS-2相对于ASS-1算法的主要优势:从下边界方向设置初始空间相较于上边界,可以减小缩放次数,更快调整到合适的搜索空间,从而提高解算效率。 图9 不同历元下ASS-1和ASS-2算法的缩放次数和解算耗时Fig.9 Scaling times and resolution time of ASS-1 and ASS-2 under different epochs 下面采用动态算例进一步验证ASS算法的性能,该组数据采集于武汉梁子湖大道。图10为共视卫星数和PDOP值序列图,由图10可知,GPS和BDS的可视卫星数均在9颗左右,PDOP值在3以内,而在GPST 204 000 s附近跑车由于受建筑物遮挡,导致可视卫星数较少。 图10 共视卫星数及PDOP值Fig.10 Number of common view satellites and PDOP value 表8统计了在不同卫星个数下的模糊度成功率。由表8可知,CLAMBDA能够显著提升弱GNSS模型下的模糊度固定成功率。图11为GPS单频基线向量解算结果,可以看出,由于CLAMBDA的模糊度固定成功率较高,可以获得较好的基线向量解算结果。 表8 不同卫星个数下的模糊度固定成功率 图11 GPS单频基线向量解算结果Fig.11 GPS single frequency baseline vector solution results 表9统计了不同卫星个数下的模糊度平均解算耗时。由表9可知,ASS-2平均解算耗时在3 ms以内,且整体解算效率最接近于LAMBDA算法,ASS-1次之,BFS解算效果较差,ASS-2整体解算效率相较于BFS可以提高1倍以上;BFS解算效率受GNSS模型强度直接影响,随着卫星数的增多而增大;ASS-1和ASS-2的解算效率呈现增大后减小的趋势,主要是当GNSS模型强度较强时,解算效率受模糊度维数的影响。 表9 不同卫星数下的模糊度平均解算耗时对比 (3) 在弱GNSS观测模型下,CLAMBDA相较LAMBDA方法可显著提升模糊度的固定成功率,对信号遮挡比较严重的地方,如城市峡谷、山区等具有较好的实际应用价值。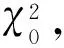
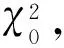
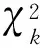
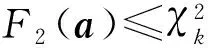

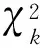

3 试验分析
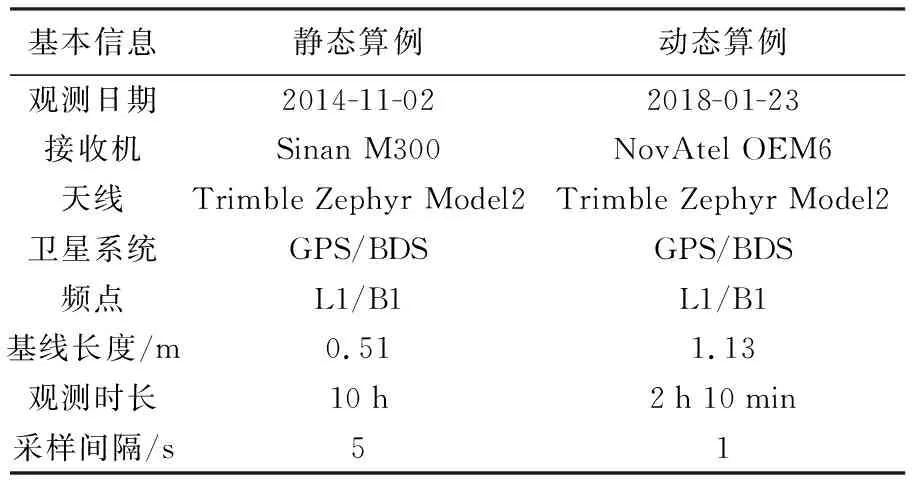
3.1 静态算例


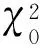





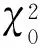

3.2 动态算例


4 结 论