标准运输工况下固态火箭发动机动力学响应仿真

鲁 棒，安振涛，李天鹏

(陆军工程大学石家庄校区，河北石家庄 050003)

1 引言

固体火箭发动机的公路运输安全性不仅关系作战保障效率，还直接影响着各项战术性能的发挥。为使火箭具备更稳定的内弹道性能，药柱设计通常采用复杂的内通道形状，使得发动机在环境载荷作用下的应力更为集中[1]。

公路运输过程中产生的随机振动载荷作用一般不会直接造成固体火箭发动机结构性破坏，但在远距离或多次运输工况下，也会导致发动机装药的累积损伤。在研究低温高应变率下HTPB推进剂的性质时，应用了沙佩型本构理论，并考虑了一个损伤变量来建立损伤演化函数，证实了所建立的本构模型是有效的，然而，由于在描述非常大应变下的变形行为时存在一些缺陷，还应进一步研究[2]。徐新琦[3]等研究分析了不同等级路面、不同运输速度对药柱随机振动响应分布的影响规律，为进一步确定药柱运输寿命提供了参考。刘华[4]则针对推进剂各材料参数对振型的影响规律进行研究，利用ANSYS对药柱振动特性进行仿真分析，并基于随机时变动力可靠度理论讨论了公路运输载荷对药柱可靠度的影响。李恩奇[5]等采用频变对的复模量模型，分析计算了某型固体火箭发动机的固有频率及振型，得到了运输过程中的随机振动响应。为进一步研究发动机在动力学载荷下的结构完整性奠定了基础，张波[6]等采用搭建的实时监测系统平台，测试得到了某型固体发动机在公路运输过程中界面的应力—温度响应变化曲线，对固体发动机公路运输的可靠性研究及界面性能改进均由重要意义。而在实际公路运输过程中，固体火箭发动机承载的是多轴随机振动载荷。孙金云[7]计算了长时间公路运输条件下，某型固体发动机药柱的累积损伤，并给出了频域的疲劳可靠度计算方法。朱卫兵[8]则基于Steinberg的“3σ”法，定量计算了由随机载荷导致的累积损伤，并预估了战斗部装药的运输失效时间。以上研究结论均为固体火箭发动机运输过程中的结构完整性评估提供了新思路和一定的技术支撑。

Gustavo[10]提出了一种基于时间和温度叠加的复合固体推进剂动态力学性能表征和主曲线构建方法，结果是充分的，为考虑循环载荷进行推进剂颗粒结构完整性评估提供了所需的数据。

本文以运输工况为主线，按照运输速度和公路等级划分，针对某型火箭弹实际装载条件，构建实体三维有限元模型，利用大型商用有限元软件施加公路运输中的振动谱，获取三种工况下固体火箭发动机各部位的应力应变云图，对于研究公路运输条件下固体火箭发动机的结构完整性具有一定参考价值。

2 火箭发动机三维有限元计算模型构建及模态分析

为体现火箭发动机整体在公路运输过程中的响应信息，根据实际几何模型，构建精确的火箭发动机三维有限元模型。

2.1 火箭发动机公路运输载荷特性及装药结构特征

图1给出了火箭发动机在钢栅包装箱内的受载特征。运输过程中，由车厢产生的垂向加速度激励A直接作用在储运箱底部，经宽为80 mm的固定环传递至发动机壳体下方。上层储运箱及火箭弹的自重则通过凸出的外钢栅包装层层传递到车厢平面，并未对下层弹体造成挤压。另外，在相邻两个松动紧固机构之间的火箭发动机壳体不与储运箱产生任何接触，保持悬空姿态。

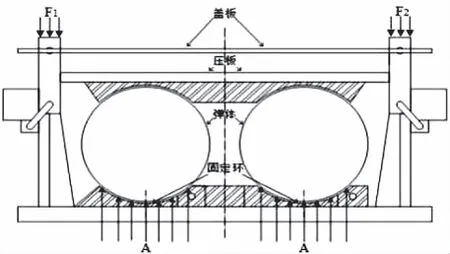
图1 松动紧固机构载荷分布

2.2 有限元模型构建及网格划分

构建的三维有限元模型全部采用六面体网格划分，各粘结界面采用等效处理，并对前、后装药端头药柱构型复杂处进行局部网格细化。其中，为准确得出火箭发动机固有频率和各阶振型，在进行模态分析时采用全模型，共划分单元153400个，节点170200个。而基于平面应变分析结果，在计算模型动力学响应时，采用1/2模型，共划分单元76710个，节点87230个。

2.3 火箭发动机三维有限元模型模态分析

实际运输过程中，火箭发动机运动受三个松动紧固装置限制，基本构成两个连接的“悬臂梁”。因此，在采用正交模态法分析有限元模型在运输条件下的固有频率时，需要对发动机壳体前端受束缚部位的6个自由度和壳体其它两个束缚部位的径向运动进行限制。图2为计算得到的发动机前20阶固有频率分布。其中，第1阶固有频率为79.829 Hz，远大于加载至火箭发动机壳体表面载荷的频率，说明运输过程中几乎不会发生共振。但高阶固有频率主要集中在138～160 Hz之间，外界其它干扰条件，如风力影响则有可能造成火箭发动机的局部共振。

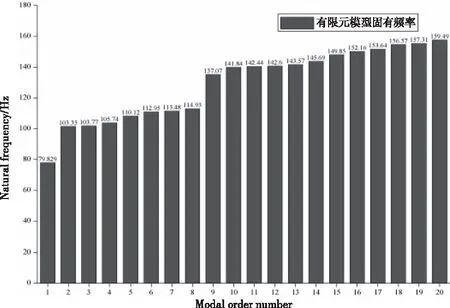
图2 发动机前20阶固有频率

2.4 三维有限元模型仿真计算工况确定

A50、B50及D40分别代表A等级公路50km/h、B等级公路50 km/h和C等级公路40km/h。各材料物理属性均取25℃环境下的测量数值。由于运输过程中激励作用部位未发生改变，火箭发动机各部件的应力应变分布大致相同[9]。因此，依据正交试验设计原则，并主要考虑公路等级与运输速度因素影响，按照加速度激励从小到大的顺序选取A50、B50和D40三种运输工况用于计算火箭发动机各部件动力学响应分布。

3 不同运输工况下的应力应变响应研究和分析

3.1 壳体

三维有限元模型的模态分析结果表明，火箭发动机装药结构的局部模态过多，不适宜采用模态叠加法分析动力学响应，因此，仍采用直接法计算模型在运输工况下的动力学响应，并以von Mises应力应变准则判定各部件结构完整性。

图3所示为火箭发动机壳体有限元模型，分别取壳体外表面上、中、下三条特征线1、2、3，以研究von Mises应力应变分布规律。其中，特征线1在载荷加载一侧，且特征线方向由前装药指向后装药。

图3 壳体有限元模型及三条特征线示意图

由于计算得到的壳体外表面应变较小，基本在10-8～10-5数量级，而作为主要承力的刚性部件，一般采用von Mises应力准则评估壳体的结构完整性，图4和图5分别给出了von Mises应力在壳体外表面的云图分布及沿特征线分布规律。结果表明：壳体表面载荷加载处仍出现应力集中，前、后两段应力云图分布基本对称；特征线1和3上应力分布基本相似，但前者应力值稍大；特征线2，即壳体中部外侧的应力要明显小于其它两条特征线的应力值。最大von Mises应力响应值出现在壳体后半段，为28.5 MPa，远小于许用强度1500 MPa，结构完整性完全得到满足，且安全系数充裕。

图4 A50运输工况下壳体外表面von Mises应力场分布云图

图6 B50运输工况壳体外表面von Mises应力场分布云图

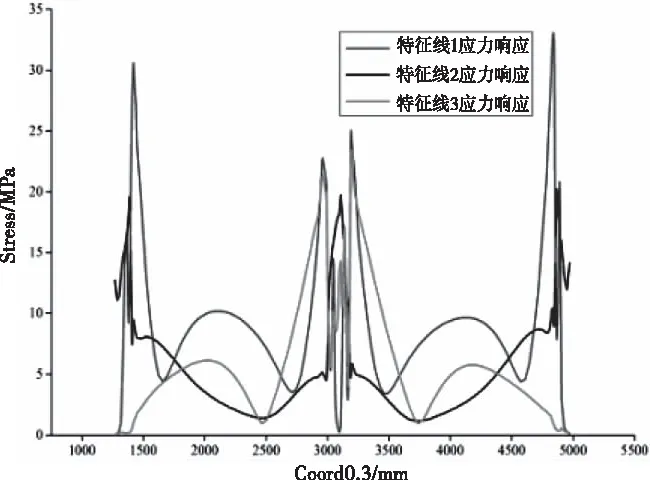
图7 壳体von Mises应力响应沿三条特征线分布规律

结果显示，特征线1，即载荷加载侧的应力响应基本保持全局最大；壳体外表面的加速度载荷作用部位的应力响应仍高于其它区域，全局最大von Mises应力响应值为41.5 MPa，出现在壳体后部。相较于A级公路运输时，应力集中影响范围有所增大，但依然满足结构完整性。

受作战环境限制，火箭有可能在D级公路运输，作用于发动机壳体外表面的加速度载荷激励将显著增加。图8所示为D40运输工况下，火箭发动机壳体外表面von Mises应力云图分布，响应最大值为145 MPa。从整体来看，von Mises应力集中同样分布在载荷作用部位，但壳体外表面低应力水平分布区域明显缩小，最大值仍出现在壳体后部。图9则给出了壳体外表面von Mises应力应变响应沿三条特征线的分布规律。特征线在中间段上的应力分布区分明显，这说明D40运输工况下的加速度激励作用明显增强。

图8 D40运输工况下壳体外表面von Mises应力场分布云图

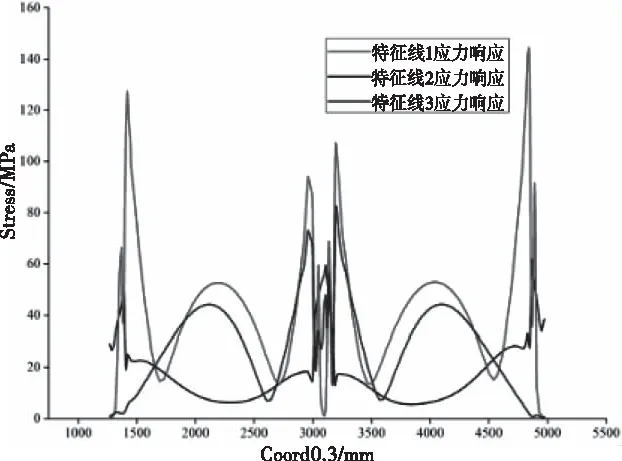
图9 壳体三条特征线的von Mises应力分布

对比分析发现，壳体在D40运输工况下von Mises应力响应的极大值相较于A50和B50运输工况有较大提升，但同样满足结构完整性要求，且仍有较大的安全裕度。壳体von Mises应力响应云图分布形式在总体上与A50、B50运输工况下的差异不大，但两端响应差值有所扩大。

3.2 药柱

在药柱内表面分别取如图10所示的七条特征线(10、11、12、…、16)，以研究公路运输条件下药柱应力应变场分布以及星尖、星根响应差异。特征线10、12、13、15、16为经过星尖的五条特征线，特征线11、14则为两条穿过药柱星根的特征线，其中特征线16分布于载荷加载侧。

图10 药柱有限元模型及内表面七条特征线示意图

图11和图12分别描述了同一时刻下，药柱von Mises应力应变场分布云图及沿特征线变化规律。计算结果表明，星型和孔型药柱前端，即载荷加载区域均出现应力应变集中；药柱最大von Mises应力、应变分别为1.31×10-2MPa和0.331%，且均出现在星型药柱前端内表面的几何突变处。对比分析发现，药柱的最大和最小von Mises应力、应变值均分布在星型药柱上，这说明星型药柱的承载分布差异较大，容易出现完整性问题。

图11 运输工况下推进剂药柱von Mises动力学响应云图分布

与平面应变分析结果相似，经过星尖前端的特征线10和特征线13应力集中现象较其它三条特征线更为显著，而药柱中间部位应力响应变化则较为平缓；另外，对比经过星根的特征线11、14上的应力应变响应可以发现：除端部存在一定的应力集中，其余部位响应值均远小于其它特征线。推进剂的高温许用应变为40%，其结构完整性能够完全满足要求，但运输过程中药柱端部承载应力集中现象显著，虽不致造成瞬时结构破坏，从远距离或多次运输安全性角度而言应适当加以防护。

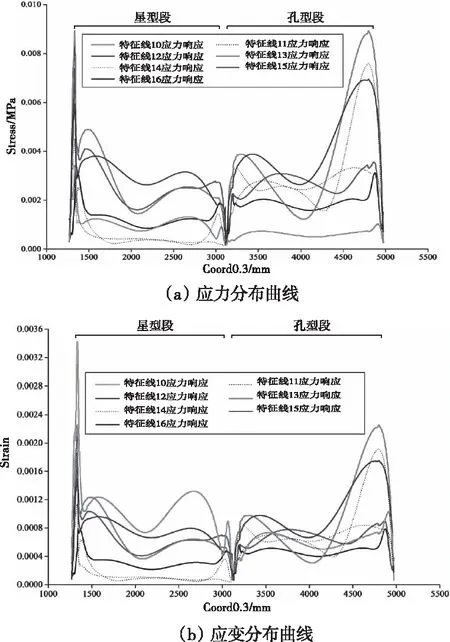
图12 药柱von Mises应力应变沿特征线分布规律

同样在药柱内表面取如图10所示的七条特征线，以研究B50运输工况下药柱von Mises应力应变场分布以及在星尖、星根处的响应差异。推进剂药柱的von Mises应力场的分布规律不仅可以反映出药柱在公路运输过程中承受的应力水平，也是评估其结构完整性的一个参考指标。因此仍有必要同时探讨药柱的von Mises应力场。

图13和图14则分别给出了同一时刻下，药柱von Mises应力、应变场分布云图及其沿轴向变化规律。计算结果显示星型药柱最大von Mises应力、应变响应值分别为3.1×10-2MPa和0.782%，而孔型药柱von Mises应力、应变响应极值同样出现在载荷加载区域的内表面，但均小于前者，分别为1.9×10-2MPa和0.478%。推进剂的高温许用von Mises应变为40%，因此其结构完整性能够完全满足要求。

图13 B50运输工况推进剂药柱von Mises动力学响应云图分布

图14 推进剂药柱von Mises应力应变沿特征线分布规律

与A50运输工况相比，星型药柱内表面几何突变处的应力集中现象更为显著，并且最大与最小von Mises应力应变响应值差异在进一步扩大，这说明星型药柱的承载分布合理性下降，运输过程中在载荷作用区域容易首先出现完整性问题。

分析图15中药柱von Mises应力、应变场分布云图发现，相邻加速度载荷作用部位的应力应变响应随轴向距离增大而迅速衰减；前、后装药过渡处的应力集中现象随公路等级下降而逐渐明显。在星型药柱前端几何突变处同样存在全局最大von Mises应力、应变响应值，分别为6.21×10-2MPa和1.57%，约为B50运输工况下响应极值的3.3倍。但推进剂在高温条件下的许用von Mises应变为40%，短时间运输不会造成结构完整性破坏。相比较而言，药柱在该公路运输条件下的安全系数最低，应是重点关注部件。根据图16中药柱von Mises应力、应变响应沿特征线分布规律可以发现，星尖上的响应一般大于星根。

图15 D40运输工况下推进剂药柱von Mises动力学响应云图分布

图16 推进剂药柱von Mises应力应变沿特征线分布规律

对比分析认为，在公路运输过程中，药柱是火箭发动机中安全系数最低的部件，可直接决定着火箭的公路运输安全性。星型药柱内表面的几何突变处在不同运输工况下的应力集中现象更为显著，但星型装药响应分布的均匀性总体上要优于孔型装药。

4 结束语

通过对火箭发动机三维粘弹性有限元模型动力学响应的计算，开展了各部件在三种不同运输工况下的结构完整性分析。主要结论如下：

1)依据实际结构特征，构建了火箭发动机三维有限元模型。通过仿真计算得到了模型在运输条件下的前20阶固有频率，确定了公路运输基本不会引起火箭发动机的结构共振。

2)基于正交试验设计准则，考虑公路等级与运输速度变化双重因素影响，进行了火箭发动机各部件在A50、B50和D40三种运输工况下von Mises应力应变响应分布的研究。动力学响应仿真分析结果表明，火箭发动机各部件在储运箱松动紧固机构处的载荷直接作用侧均会产生应力集中现象，其影响范围随着运输路况等级下降而扩大。

3)火箭发动机在运输工况下的结构完整性基本不受影响，但药柱在运输过程中的安全系数始终是最小，应作为火箭发动机整体结构完整性研究的重点分析对象。响应分布受公路运输等级和运输速度的共同影响，公路运输等级越低，响应极值也就越大。