基于干扰观测器的四旋翼吊挂系统非线性控制

赵永生，陈欣宇，范云生

(大连海事大学船舶电气工程学院，辽宁 大连 116026)

1 引言

近年来，由于飞行器起降方便，移动不受地形影响等特点[1，2]，越来越多的研究人员从事飞行器的开发研究工作，飞行器的使用也越来越普及，多使用于航拍领域如影视拍摄、新闻报道、电力巡检、环境监测等使用摄像机的领域[3]，因此世界海关组织协调制度委员会(HSC)将之归类为“会飞的照相机”。随着飞行器的发展，开始出现飞行器吊挂负载的应用，吊挂运输在快递运输及危险地区救援等方面均有突出表现[4，5]。如何控制四旋翼飞行器吊挂系统成为新的研究热点[6]。

四旋翼飞行器吊挂系统是一个多自由度、强耦合、欠驱动的复杂系统，控制难度很大[7]。其增加的两个摆角自由度加剧了系统的耦合程度，使系统的控制难度大大提升，尤其吊挂摆角不能直接控制，需通过飞行器位置来间接控制，并且易受外界甚至飞行器旋翼旋转产生的风的干扰影响，进而破坏整个吊挂系统的稳定。

许多学者对四旋翼吊挂系统进行了深入研究。文献[8]用能量分析的方法设计了四旋翼无人机吊挂飞行系统的非线性控制器，在抑制吊挂物摆动的同时飞行器也能到达目标位置。文献[9]将系统模型转换为开环结构的有限时间差分博弈问题，与纳什均衡解和滚动优化的思想相结合，设计了基于状态反馈的滚动纳什控制器。文献[10]通过动态反馈将系统转化为线性能控系统，并设计了动态反馈控制律。文献[11]将四旋翼吊挂系统建立为差速混合动力系统，设计了非线性控制器，使飞行器姿态及负载姿态控制器全局指数稳定。文献[12]对负载质量变化的情况设计了鲁棒滑模控制器(SMC)，可快速跟踪所需轨迹，同时抑制抖动。文献[13]引入虚拟力用于位置控制，使用反步法四旋翼姿态控制和负载摆角控制将实际推力驱动到该虚拟力，从而实现轨迹跟踪。

当前的研究已经较为完善，但仍存在一些不足之处，体现在未对吊挂负载设计控制器，对吊挂负载所受干扰考虑不够充分，仅利用控制器的鲁棒性减小干扰影响。

结合前人经验，本文对上述问题进行了优化[14-19]。首先为吊挂负载设计控制器，将其对飞行器的整体干扰转化为对飞行器位置的干扰，不影响飞行器的姿态响应；其次针对吊挂负载易受干扰问题设计了干扰观测器估计所受干扰并修正；最后设计了四旋翼吊挂实验平台验证设计方案。文章结构如下：第一部分运用牛顿-欧拉及拉格朗日方法[23]建立四旋翼吊挂系统的数学模型；第二部分针对吊挂负载干扰问题设计干扰观测器观测负载所受干扰并返回修正；第三部分为四旋翼吊挂系统姿态、位置及摆角三部分的控制器设计；第四部分为实验平台的搭建及验证。

2 数学模型的建立

四旋翼吊挂系统有四个输入、八个自由度，是一个高度耦合、高度欠驱动的复杂系统，不能简单将吊挂负载当作干扰处理，需要在传统四旋翼飞行器模型的基础上建立新的四旋翼吊挂系统模型，其示意图如下：

图1为建立的四旋翼吊挂系统示意图，其中飞行器为常见十字形四旋翼飞行器。以飞行器质心点为原点o建立坐标系，给出各参数定义如下：飞行器前后方向为X轴方向且后退为负，左右方向为Y轴方向且向右为正，上下方向为Z轴方向且向上为正；飞行器绕X轴旋转角度为横滚角φ且向右转动为正，飞行器绕Y轴旋转角度为俯仰角θ且向下转动为正，飞行器绕Z轴旋转角度为偏航角ψ且向右转动为正。α摆角为吊挂绳与飞行器xoz平面夹角，β摆角为吊挂绳与飞行器yoz平面夹角，L为吊挂绳索长度。令四旋翼质心到电机轴心长度为l，飞行器质量为M，负载质量为m。在对四旋翼吊挂系统进行建模时，由于系统较复杂、模型不确定性等因素的影响，需对模型做出一些简化：忽略空气阻力对飞行器吊挂系统的影响，认为吊挂绳是刚性的且质量不计，吊挂绳的悬挂点为飞行器质心。

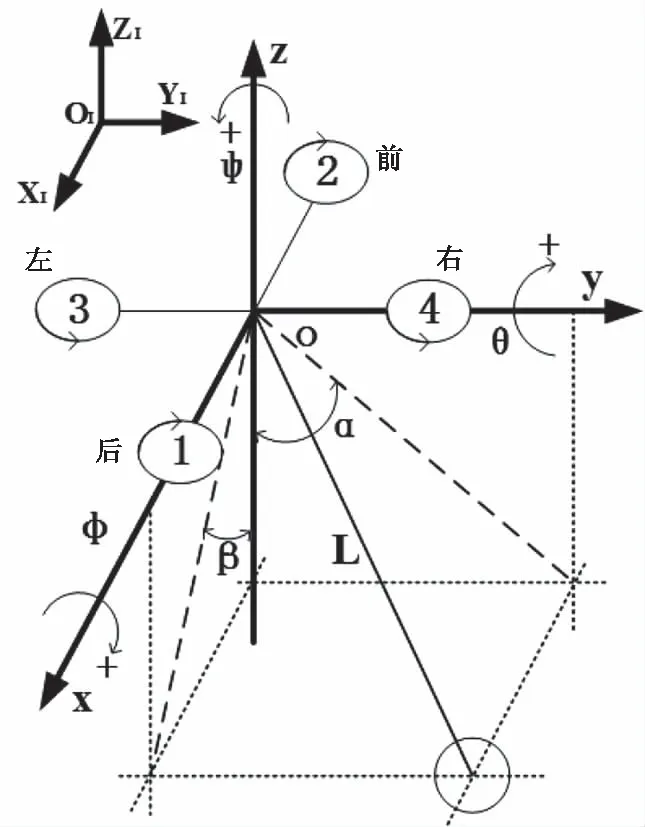
图1 四旋翼吊挂系统模型

传统四旋翼飞行器数学模型为

(1)

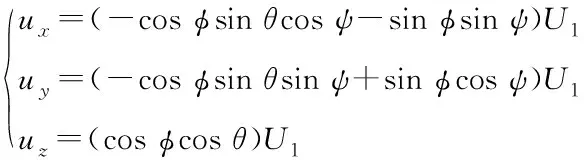
其中，U1代表四个旋翼产生的总升力，U2代表横滚力，U3代表俯仰力，U4代表偏航力矩。g代表重力加速度，Ix、Iy、Iz代表机体绕相应坐标轴的转动惯量。

在传统四旋翼飞行器的基础上，四旋翼吊挂系统增加了吊挂物，通过对四旋翼及吊挂物进行受力分析来建立四旋翼吊挂系统的数学模型。

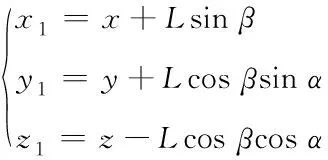
(2)

对其两边进行二阶求导，即可得吊挂物加速度与四旋翼飞行器加速度之间的关系

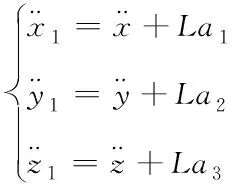
(3)

且

由加速度关系式可对其进行受力分析

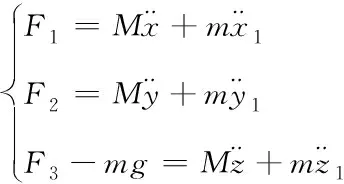
(4)

将式(1)和式(3)代入式(4)，得：

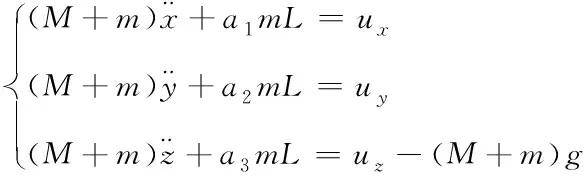
(5)

采用哈密尔顿原理及拉格朗日公式计算系统总动能

(6)

A为四旋翼吊挂系统总动能，P为系统势能，系统总动能A为

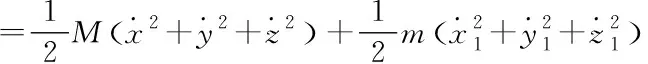
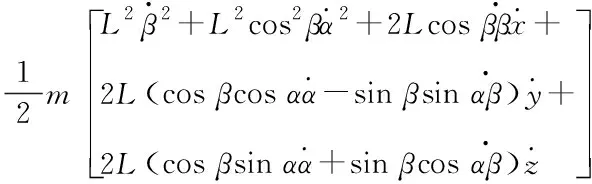
(7)

认为地平面是零势能，可得系统的势能P为

P=(M+m)gz-mgLcosβcosα

(8)

得到系统总动能及势能后，将其代入拉格朗日公式，qk取α和β，计算后可得吊挂物摆角加速度与四旋翼飞行器加速度之间的关系式

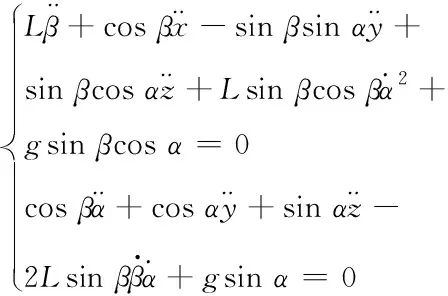
(9)

由式(1)、(5)、(9)得八自由度的四旋翼吊挂系统数学模型

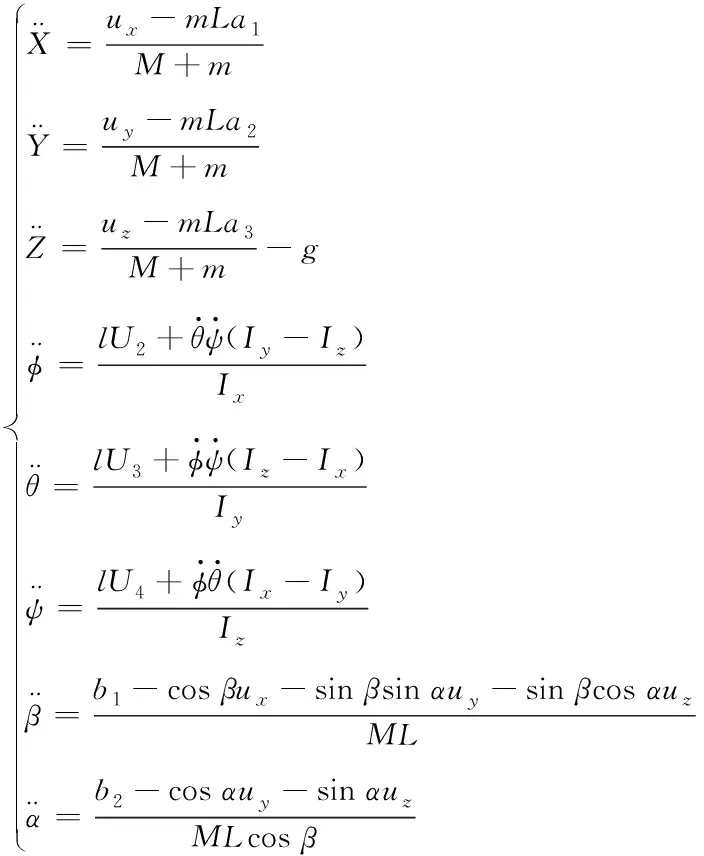
(10)

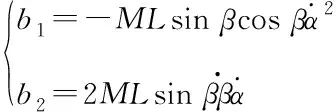
由式(10)可知，吊挂物的摆角加速度与四旋翼飞行器的加速度相互耦合，吊挂物的摆动会影响飞行器的稳定，而飞行器的移动又会影响吊挂物的摆动。因此需分别对吊挂物摆角及飞行器位置设计控制器，并且吊挂物易受各类外界干扰影响，为其设计干扰观测器以修正干扰影响。

3 干扰观测器的设计

吊挂物摆角为四旋翼吊挂系统欠驱动程度最深的部分，并由于其悬挂运输方式，极易受到外界风干扰、飞行器螺旋桨转动产生的风干扰及飞行器本身震动的干扰，因此需设计干扰观测器对吊挂物摆角所受干扰进行估计和修正。以吊挂物摆角β为例设计摆角干扰观测器。

在式(10)的摆角数学模型中加入模型不确定性及外界干扰力矩影响，得到新的数学模型如下

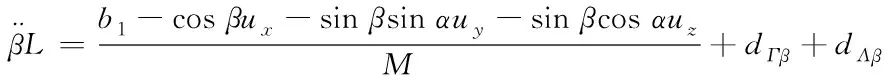
(11)

其中dΓβ表示模型不确定性，dΛβ表示外界干扰，模型总干扰为

dβ=dΓβ+dΛβ

(12)

由式(10)、(12)得系统摆角新的数学模型

(13)

将式(13)写作仿射非线性系统格式

x=f(x)+g1(x)u+g2(x)d

(14)

得

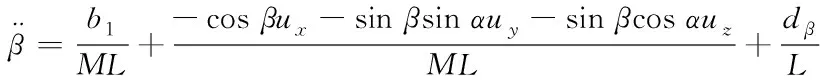
(15)

为提高系统的鲁棒性，需对干扰dβ进行补偿，设计非线性干扰观测器对干扰dβ进行观测

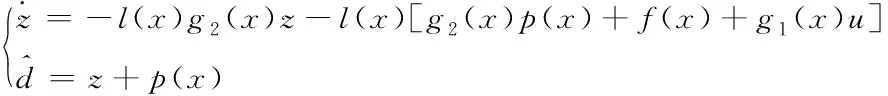
(16)

设计吊挂物β摆角的干扰观测器如下

(17)

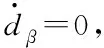
由此可以得到误差导数为

(18)

由式(17)、(18)得

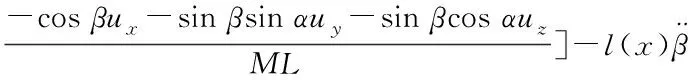
(19)

代入式(13)

=l(x)u＿dβ/L-l(x)dβ/L

=-l(x)ed/L

(20)

由式(20)可知，选取合适的l(x)可使系统渐进稳定，随时间变化扰动估计误差将趋于零。

同理可得吊挂物α摆角干扰观测器

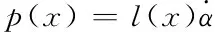
(21)

4 控制器的设计

四旋翼吊挂系统为四输入、八输出的强耦合欠驱动系统，并且多个变量均易受干扰，因此需要设计干扰观测器对干扰进行估计和补偿，并为每个自由度设计控制器来控制。其控制部分可分为四个子系统：可直接驱动的高度及偏航子系统，内环控制的姿态子系统，外环控制的飞行器位置子系统，外环控制的吊挂物摆角子系统。其控制流程图如下

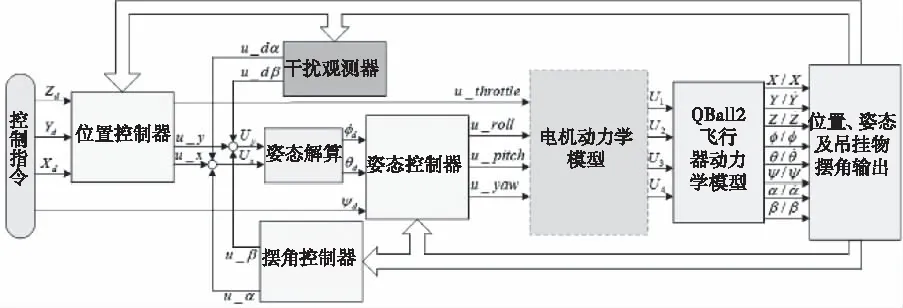
图2 四旋翼吊挂系统控制流程

飞行器横滚角和姿态角对飞行器的位置影响较小，因此将其忽略作小角度近似，得位置-姿态转换公式如下

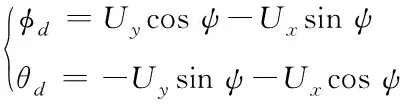
(22)

及电机模型转换公式如下

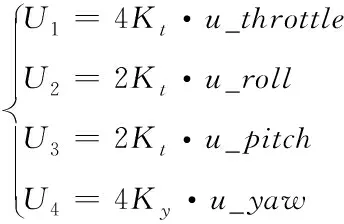
(23)

Kt、Ky为升力系数和反扭矩系数。

4.1 位置控制器设计

四旋翼吊挂系统的位置控制器、姿态控制器及摆角控制器均采用积分型反步法控制器。相比于传统的反步法，积分型反步法在消除静态误差、减小模型不确定性以及外界影响方面有优势。

以四旋翼吊挂系统飞行器高度通道为例设计控制器，高度期望值Zd与实际值Z的差为

z1=Zd-Z

(24)

对式(24)求导，得其跟踪误差的导数

(25)

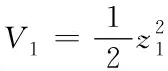
(26)

对其求导，得

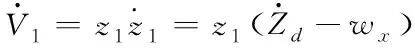
(27)

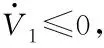
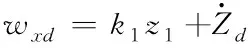
(28)

在虚拟控制量后加入了积分项，可增强控制器的鲁棒性、消除模型不确定性的影响

(29)

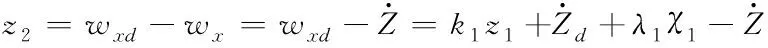
(30)

代入式(27)，得

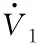
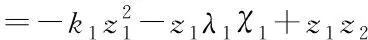
(31)

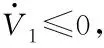
(32)

对式(30)求导

(33)

将飞行器高度数学模型式(10)代入式(33)

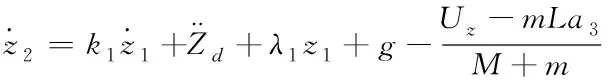
(34)

则

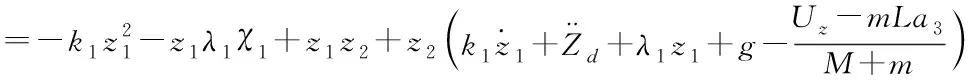
(35)

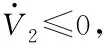
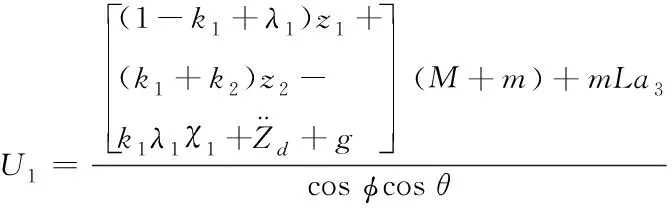
(36)

式中，k2为大于0常数。将式(36)代入式(35)，得

(37)

由式(32)(37)可证明所设计的控制律令高度渐进稳定。

同理可得飞行器位置控制器的控制律

(38)

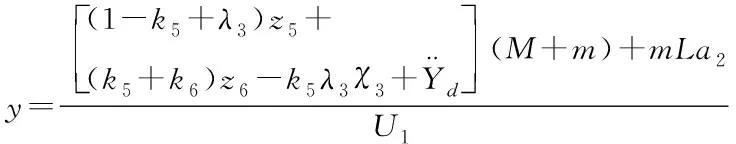
(39)

其中kn(n=3…6)、λi(i=2，3)为大于0常数，且

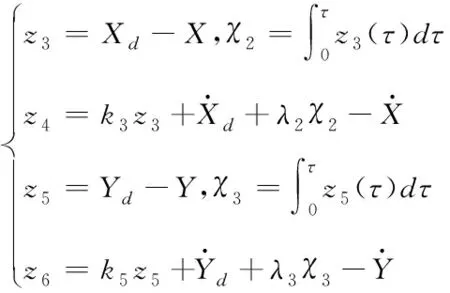
(40)

4.2 吊挂物摆角控制器

吊挂物摆角由于其欠驱动的特性，无法直接控制，需通过控制器将其转化为位置信号间接控制。控制器采用积分型反步法控制器，设计方法与上文类似，故省略详细过程，得

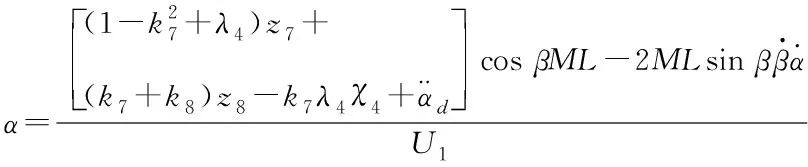
(41)

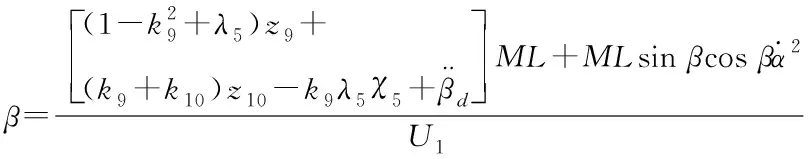
(42)

其中kn(n=7…10)、λi(i=4，5)为大于0常数，且

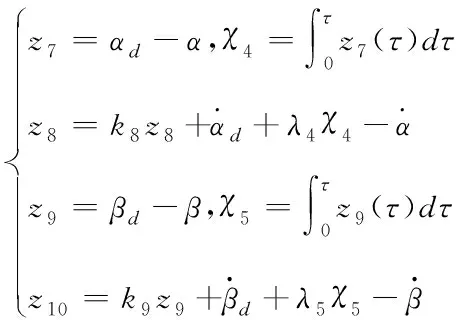
(43)

由式(38)、(39)得到飞行器位置控制器控制量和式(41)、(42)得到的吊挂物摆角控制量及式(17)、(21)得到干扰观测器的补偿量，可得四旋翼吊挂系统的飞行器位置控制量

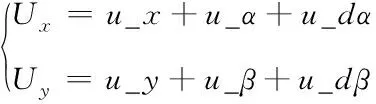
(44)

4.3 姿态控制器

得到飞行器位置控制量后，经式(22)将其转化为姿态角控制量。飞行器姿态角控制为系统的内环控制，采用积分型反步法控制，方法同上，在此仅给出结果

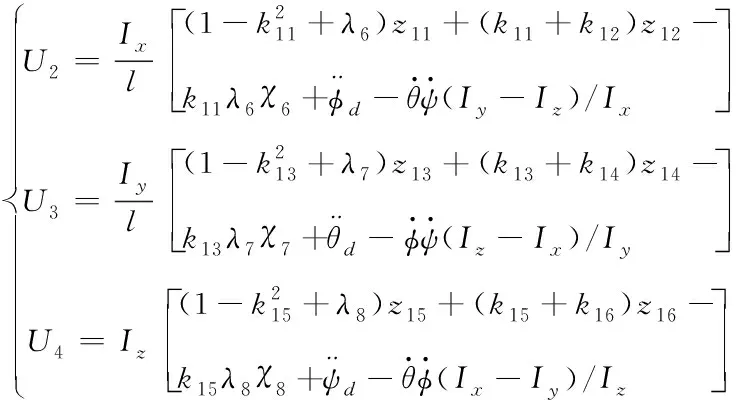
(45)

其中kn(n=11…16)、λi(i=6，7，8)为大于0常数，且

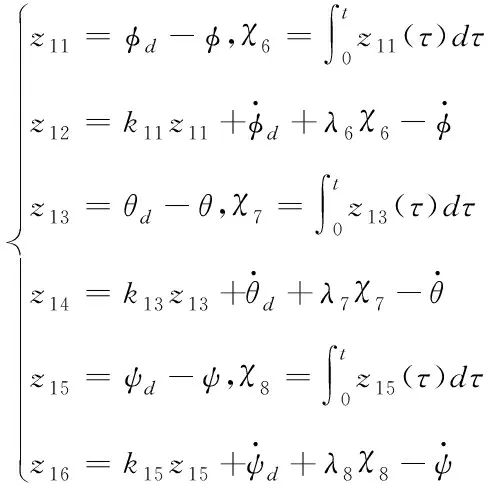
(46)

5 仿真验证

仿真在MATLAB/Simulink中运行，四旋翼飞行器采用Quanser公司生产的QBall2的参数，吊挂负载为0.2kg重心为中心的圆球，吊挂绳长1.5m，系统参数如表1。

表1 模型参数

由图3-5可知，吊挂物的摆动会影响四旋翼飞行器的稳定性，尤其对飞行器位置影响较大，积分型反步法可以有效降低摆动带来的干扰。

图3 飞行器高度变化

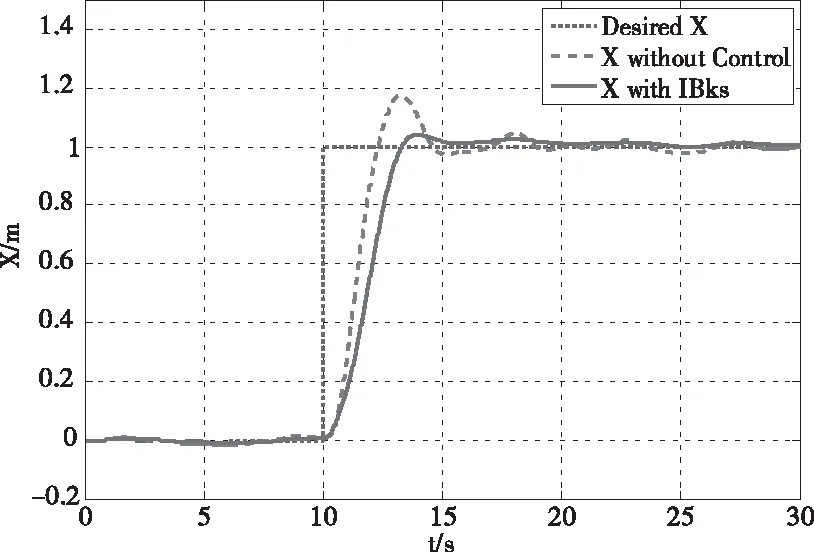
图4 飞行器X位置变化

图5 飞行器Y位置变化

由图6、7可知，在没有摆角控制器的时候，吊挂物会产生较大的摆角，不利于吊挂系统的稳定，而加入摆角控制器后可以将摆角降到较小的值，且可快速稳定。

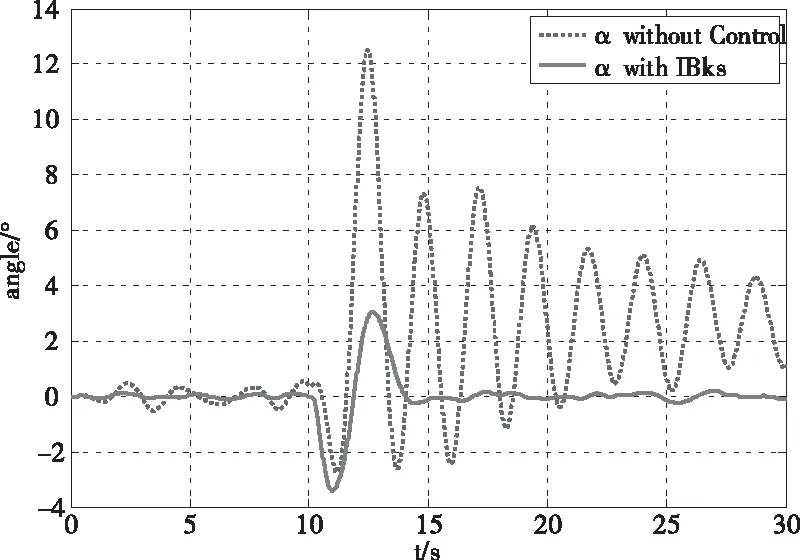
图6 吊挂α摆角变化

图7 吊挂β摆角变化

由图8、9可知，在受干扰影响后，不加入干扰观测器时吊挂摆角会出现较大的震动，不利于系统的稳定，而加入干扰观测器可以有效地降低干扰的影响。由图10可知干扰观测器不仅能观测出加入的干扰，同时还能观测出飞行器移动对吊挂摆角带来的干扰。

图8 吊挂α摆角DOBC下变化

图9 吊挂β摆角DOBC下变化

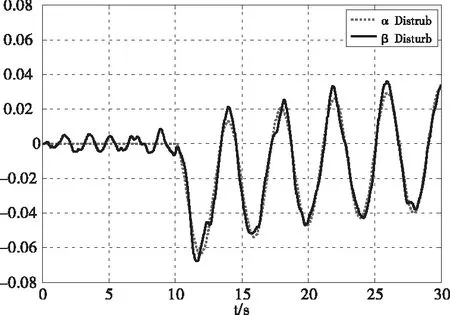
图10 干扰观测器观测的干扰

图11-14为飞行器姿态及电机相关量，从中可知飞行器在飞行过程中各项参数均处于正常范围内，证明了该系统的可行性。

图11 飞行器姿态角变化

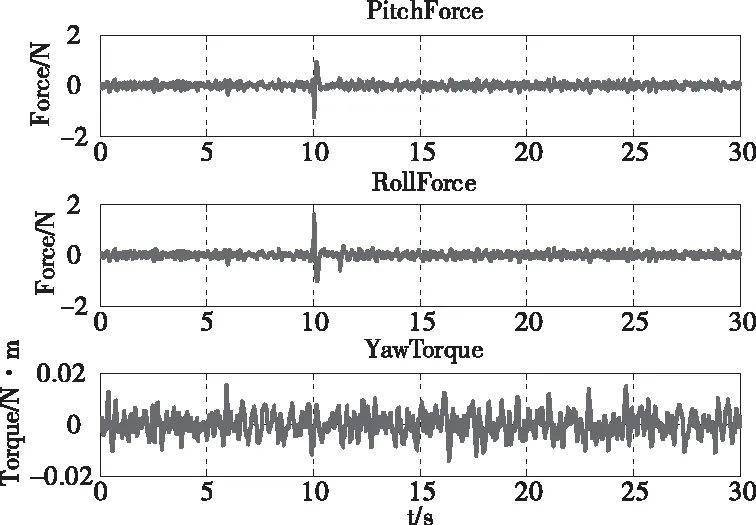
图12 飞行器姿态力矩变化

图13 飞行器姿态控制量变化

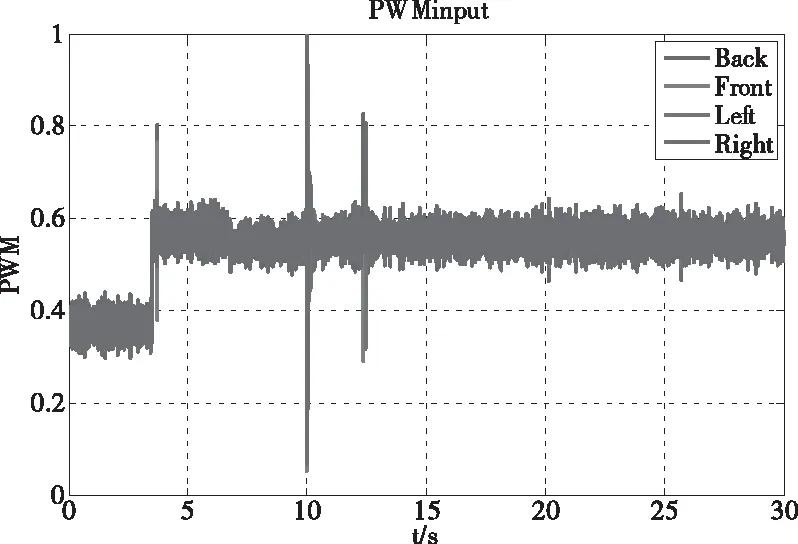
图14 电机PWM控制信号

6 结论

本文主要针对四旋翼吊挂系统的吊挂物摆动问题。首先为系统建立了数学模型，然后为飞行器位置、姿态及吊挂物摆角设计了积分型反步法控制器，并针对吊挂物易受干扰的情况设计了摆角干扰观测器对干扰进行估计和补偿。最后在MATLAB/Simulink中搭建仿真模型对搭建的数学模型及控制器、观测器进行验证，仿真表明设计的非线性控制器可以有效降低吊挂物摆动对飞行器造成的影响，同时设计的干扰观测器能观测出外界干扰的影响并补偿，可增强系统的鲁棒性，降低干扰带来的误差，对四旋翼吊挂飞行运输带来一种有效可行的方案。