基于需用功率预测的直升机/发动机综合控制方法

2022-11-28杜紫岩彭晔榕张海波

航空发动机 2022年5期

杜紫岩，彭晔榕，宋劼，汪勇，张海波

（1.中国飞行试验研究院，西安 710089；2.南京航空航天大学能源与动力学院，南京 210016）

0 引言

直升机除了运输人员物资等[1]军事用途外，在地震救援等民用领域也发挥着不可取代的作用。而直升机性能的提高一直是设计研发的不懈追求，在直升机/发动机硬件设备已经达到技术水平瓶颈的情况下，要进一步提高其性能，只能依靠控制系统的设计[2]。直升机各部件之间、直升机与发动机之间耦合性很强，相互影响，关系复杂[3]。为了使控制方法设计与实现更简便，直升机控制系统和发动机控制系统常常是独立的。独立的控制系统需保留足够的安全裕度防止连接时出现安全问题，极大的牺牲了发动机的性能[4-6]。直升机的性能不仅取决于其本身，很大程度上也受限于发动机性能[7]。

各国都对综合控制方法的设计进行了尝试，以提高发动机的性能。Frederick等[8]设计了一种综合控制方法有效提高了发动机稳定性，根据横向周期变距指令预测主旋翼扭矩的变化，从而在左右侧滚操纵期间将发动机和主旋翼转速下垂和超调降至最低；Frederick等[9]还根据飞行员偏航输入燃油补偿信号，降低突然偏航机动期间发动机和旋翼转速下垂和超调的影响。然而这2种方法使用范围有限，只在一种飞行状态下起作用。Paramour等[10]实施的“飞机/发动机综合控制”计划能够加快发动机响应，且可根据直升机的飞行状态调整发动机动力涡轮转速以保证发动机转速平稳；Wang等[11]基于增量非线性动态逆的原理，提出一种基于发动机所需扭矩与实际输出扭矩误差的前馈控制方法，与常规的总距前馈和扭矩预测前馈控制[12-13]相比，能有效地降低动力涡轮相对转速的超调量约14%。上述方法用于前馈的量都是对直升机功率的近似表征，或者使用条件受限，不适合所有飞行任务，都存在不足。

本文在UH-60A综合仿真平台的基础上，采用多元拟合的逐步回归分析法获得了直升机需用功率的预测模型，根据预测所得功率，综合考虑直升机大包线多种飞行任务进行线性前馈补偿，形成了直升机/发动机综合控制律。

1 直升机需用功率预测模型

根据气体动力学原理及直升机飞行原理[14-15]可知，直升机的需用功率WHPP受多个输入量或状态量的影响，包括前向速度Vx、横向速度Vy、垂向速度Vz、高度H、旋翼转速Ω、旋翼总距θ0、尾桨总距θT、横向周期变距θ1c、纵向周期变距θ1s、俯仰角θ、滚转角φ、航向角ψ等。在建立直升机需用功率预测模型时，为了简化计算，只采取5个量作为直升机预测模型的输入。

由于影响直升机需用功率的变量很多，且直升机的强耦合性使这些变量之间可能存在多重共线性，会对预测模型回归系数的精度造成影响[16]，为了选取对直升机需用功率影响最大的5个量，采用逐步回归分析法。

逐步回归分析法可以自动在给定的众多自变量中选取对因变量影响最大的变量形成回归方程。从1个变量开始，在前一个回归方程的基础上，逐步引入对因变量作用最显著的自变量，剔除已引进自变量中不显著的量。一次引入和剔除为逐步回归的一步，每步都需要F检验以保证新的引入仍是最优方程。重复这一过程，直到没有显著的自变量可以引入或者剔除，则回归模型建立完毕[17]。因此主要过程可以分为引入变量和剔除变量2部分。

（1）变量引入依据。

假设方程中已含有l个自变量，则此时的回归方程为

记上述回归方程总的离差平方和为TSS，回归平方和为RSS（x1，x2，…，xl），剩余离差平方和ESS（x1，x2，…，xl）。则有样本容量为n，新自变量xi（i=l+1，l+2，…，n）引入后的回归方程为

则总的离差平方和为

由于总的离差平方和不变，因此引入新的变量后残差平方和ESS会减小，令

式中：PSSi（x1，x2，L，xl）称为xi对因变量的方差的贡献，也叫xi的偏回归平方和。

将PSSi（x1，x2，L，xl）与剩余平方和ESS（x1，x2，L，xl）比较，检验xi影响是否显著，即

求取Fin-i中最大值

选取合适的引入变量F检验临界值Fin，并与Fin-k比较。若Fin-k＞Fin，则引入相应的xi，否则不引入变量。

（2）变量剔除依据。

假设已有l个变量引入方程中，依次剔除1个自变量xi（i=1，2，…，l）后，回归方程的总离差平方和为

则对应xi的贡献为

计算并求其最大值

选取合适的剔除变量F检验临界值Fout，并与Fout-k比较。若Fout-k＜Fout，则剔除相应的xi，否则不剔除变量。在剔除相应的xi后，需要对方程中剩下的变量继续进行上述剔除显著性检验，直到没有可以剔除的变量存在为止。

对直升机的相关可测参数进行逐步回归分析可知，旋翼总距θ0、旋翼转速Ω、前向速度Vx、尾桨总距θT、俯仰角θ这5个变量对直升机需求功率的影响最为显著。因此，可结合上述5个变量建立如式（12）所示的直升机需求功率预测模型，利用当前时刻的θ0、Ω、Vx、θT、θ超前预测下一时刻的直升机需用功率。

式中：x=[θ0,Ω,Vx,θT,θ]；y=WHPP。

模型精度如图1所示。从图中可见，除个别点外，直升机需用功率模型预测相对误差eHPP均在7%以内，满足工程实践需求。

图1 直升机需用功率预测模型相对误差

2 直升机/发动机综合控制方法设计

涡轴发动机控制系统

的主要目标是在保证动力涡轮转速恒定[18]的前提下，最大限度地提高涡轴发动机的动态响应速度。涡轴发动机通常采用串级控制结构，主要包括燃气涡轮转速控制副回路与动力涡轮转速控制主回路。而本文提出的基于直升机需用功率预测的直升机/发动机综合控制方法在燃气涡轮转速指令的位置加入前馈控制，采用所建立的需用功率预测模型进行线性前馈，综合控制系统结构如图2所示。

图2 综合控制系统结构

根据如式（12）所示的直升机需求功率预测模型可以得到下一时刻WHPP。

最简单易实现的方法是对WHPP进行线性前馈。因为发动机燃油的变化通过控制主回路，根据燃气涡轮转速的变化进行调节，二者是线性关系，燃气涡轮转速的变化进一步受发动机输出功率影响，这二者也是线性关系，而发动机输出功率由直升机需用功率决定，应稍大于等于直升机需用功率，也就意味着发动机燃油与直升机需用功率是线性关系。

在地面标况下，使燃气涡轮转速从65%变到110%，当直升机达到稳态时，燃油流量与直升机需用功率的关系如图3所示。图中WHPP%为以燃气涡轮转速100%时WHPP的值为基值归一化后数据。Ng%-Wfb稳态工作线和Ng%-WHPP%稳态工作线如图4所示，WHPP%-Ng%稳态工作线如图5所示。

图3 WHPP%-Wfb稳态工作线

图4 Ng%-Wfb稳态工作线和Ng%-WHPP%稳态工作线

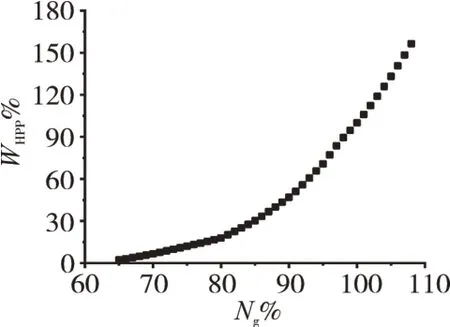
图5 WHPP%-Ng%稳态工作线

从图3~5中可见，在整个区间内，燃气涡轮转速与燃油流量之间、燃气涡轮转速与直升机需用功率之间是分段线性关系，直升机需用功率与燃油流量也是线性关系。这种关系适用于燃气涡轮转速变化的全范围，在整个飞行包线内这种线性关系也成立，因此线性前馈最直接有效。

为了防止线性前馈时补偿过度，根据WHPP的变化率对线性前馈信号的系数进行调整，使其在WHPP变化剧烈的情况下，前馈补偿量不会过大或者过小。

线性前馈不用对前馈量进行其他改变，只相当于量级的放缩，因此也不会改变所需功率的变化趋势。在直升机/发动机综合控制中也常采用总距-油门杆联动，就是利用总距可以反映功率这一特性。

但是总距补偿只对大的机动动作有效，不能反映功率细微的变化。直接采用需用功率对燃油进行补偿，可以更准确的使燃油快速达到期望。

3 直升机/发动机综合控制方法仿真验证

直升机/发动机综合仿真平台为UH-60A综合模型[19]，其结构如图6所示。在直升机/发动机综合仿真平台上验证所设计的控制方法，并与加总距前馈的串级PID控制、常规串级PID控制相比较，仿真结果如图7所示。

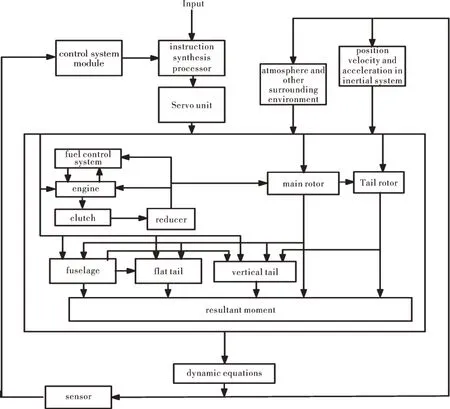
图6 直升机/发动机综合仿真平台

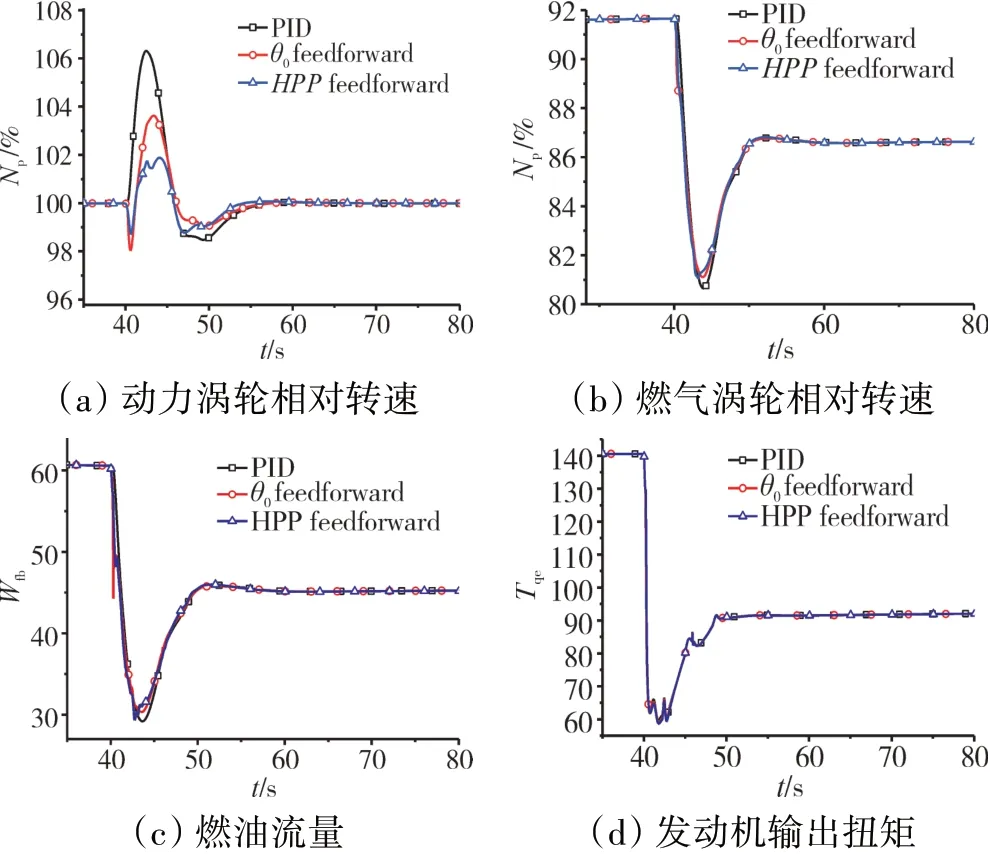
图7 在H=0.4km，需用功率减小时控制效果对比

飞行高度H=0.4 km保持不变，在t=40 s时，前飞速度从20 m/s减小为0，横向速度从0增大到10 m/s，此飞行一直保持到仿真结束，3种对比案例选取的串级PID参数一致。

由仿真结果可知，在低速段前飞减速，如图7（a）所示的动力涡轮相对转速高于设定值100%，这是因为此时直升机需用功率急剧增大。对于旋翼而言，转速减小，其需求功率减小，由于涡轴发动机采用恒转速控制方案，即其动力涡轮转速保持在100%左右，则发动机输出扭矩相应减小以减小其输出功率，从而燃油流量迅速减少，涡轴发动机输出扭矩减小。加入了需用功率前馈控制通过超前预测直升机需求功率，对涡轴发动机进行扰动补偿，从而显著减小了涡轴发动机的超调量。相比于串级PID控制方法，采用带总距前馈控制的串级PID方法预测需用功率前馈控制可以使动力涡轮转速的超调量减小70%左右，且响应时间缩短了2 s以上，相比于带总距前馈控制的串级PID方法，可以减小48%。

在飞行高度H=0.5 km，直升机保持悬停状态，在t=40 s时，开始以10 m/s的速度进行爬升，并保持此飞行条件直到仿真结束，仿真结果如图8所示。

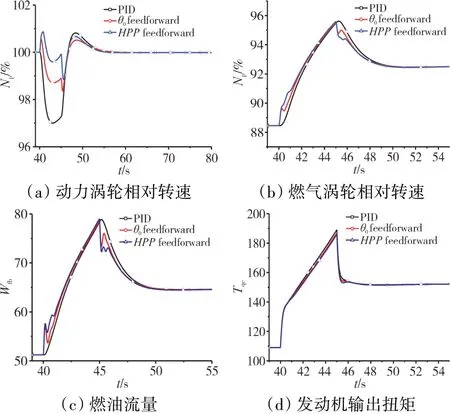
图8 最大爬升速度飞行时控制效果对比

由结果可知，直升机在爬升时，旋翼总距增加，拉力增大，旋翼转速增大，需要发动机输出更大的功率，因此发动机所需的燃油也会突然增大，但是由于发动机响应的不够及时，会使发动机动力涡轮转速下垂，引入需用功率前馈后，有效减少了发动机动力涡轮转速的下垂量，相比一般PID控制减小了65%左右，响应时间缩短了1 s左右，相比总距前馈减小了29%。

在飞行高度H=1.2 km、前飞速度10 m/s的条件下，当t=180 s时，保持高度不变，前飞速度增大为30 m/s，以此飞行条件飞行，到t=240 s时，飞行条件变为H=1.6 km、前飞速度增大到50 m/s，并保持至仿真结束，仿真结果如图9所示。

图9 在H=1.2km，前飞速度变化时控制效果对比

从图中可见，当直升机高度保持不变，前飞速度在低速段增大时，直升机的拉力在减小，所需发动机提供的扭矩也减小，发动机供油也随之减少，此时旋翼转速减小，而发动机的延迟响应导致了发动机动力涡轮转速的超调，需用功率前馈使得响应加快，超调减小62%，总距前馈只减少42%左右，相比总距前馈改善了20%超调量。当直升机的飞行高度增加，前飞速度在高速段增大时，直升机的拉力明显增大，因此发动机所需的燃油也会突然增加以输出足够大的扭矩供给直升机，旋翼转速增大，发动机动力涡轮转速下垂，需用功率前馈使其下垂量减小62%，相比总距前馈减小25%左右，响应时间缩短了3 s以上，证明所设计的控制器具有优越的鲁棒性能。