薄壁结构干摩擦阻尼减振设计分析
2022-11-28高世民王延荣
高世民,王延荣,叶 航
(北京航空航天大学能源与动力工程学院1,北京100083,江西研究院2,南昌 330096;3.成都航利(集团)实业有限公司,四川彭州 611936)
0 引言
航空发动机转子叶片、整体叶盘、篦齿封严结构、薄壁齿轮和减涡器引气管等属于典型的薄壁结构,在工作过程中承受着很高的离心载荷、热载荷导致的静应力,以及变化载荷导致的振动应力,容易出现高循环疲劳失效,使得降低结构所受静应力及控制其敏感阶次振动应力成为必要[1-2]。然而,薄壁结构在工作中的激励频率范围宽、激励阶次多,难以避开所有共振点。通过摩擦耗散振动能量的干摩擦阻尼减振是降低薄壁结构振动应力的有效技术手段[3]。
薄壁结构干摩擦阻尼减振设计依赖于对薄壁结构动力学和接触问题的把握,重点关注共振频率、阻尼和振动应力水平等[4]。接触模型刻画了弹性体(通常为金属)干摩擦接触时的相互作用,及其与接触面间相对运动的关系[5]。目前,接触模型可分为1D模型[6-7]和2D模型[8-9];恒 定[6,8]或 者变法 向正压 力[7,9]模型;宏滑动和微滑动模型[10]。利用发展的接触模型可计算分析系统的动力响应。直接的时间积分法非常耗时,Phadke等[11]计算带缘板阻尼器叶片1个激励频率点下的响应便需40 h。而在设计阶段无法承担如此高昂的时间成本。考虑到薄壁结构响应往往具有周期性,Cardona等[12]采用谐波平衡法将运动方程由时域微分方程转换为频域代数方程,进而高效求解此非线性方程。为能更有效地描述接触,在谐波平衡法基础上,Cameron等[13]提出了时频转换法,将频域位移转换到时域后,在时域内求解非线性接触作用力后再转换回频域。为进一步提高计算效率,Mehrdad[14]采用模态综合法,Petrov[15]采用频率响应函数法,利用减缩模型计算叶盘结构的非线性响应;Krack等[16-17]从非保守系统角度利用非线性模态来处理干摩擦问题;Hüls等[18]采用幅频响应曲线来评价减振结构的阻尼效果。然而,响应计算存在实际激励大小难以确定、计算时间长和收敛困难等问题[4]。值得注意的是,航空发动机工作中薄壁结构典型状态的稳态应力和许用的振动应力范围已基本确知。
本文从薄壁结构振动应力出发,基于能量耗散发展了一种减振结构阻尼效果的分析方法及流程。
1 干摩擦系统运动模型
航空发动机薄壁结构设计中常见的干摩擦阻尼器形式主要有缘板阻尼器、叶冠、凸肩、阻尼环、阻尼套筒。其中前三者主要用于叶片结构,阻尼环主要用于齿轮、叶盘和封严篦齿,阻尼套筒主要用于封严篦齿和减涡器引气管,航空发动机典型薄壁结构及其干摩擦阻尼器结构形式如图1所示。
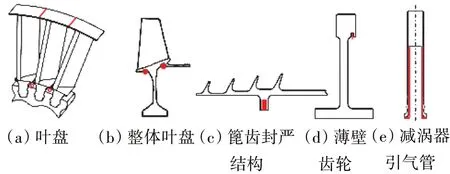
图1 航空发动机典型薄壁结构及其干摩擦阻尼器结构形式
1.1 运动方程
含干摩擦作用的薄壁结构运动方程为

式中:M、C和K分别为薄壁结构的质量矩阵、阻尼矩阵和刚度矩阵;u(t)为结构的位移列向量;fe(t)为结构受到的激振力列向量;fc为干摩擦接触面上非线性接触作用力列向量,只在接触面自由度上不为0。
由式(1)可看出干摩擦阻尼减振包含了经典振动和接触2方面内容。本文的目的是分析减振结构提供的干摩擦阻尼;若需考虑材料阻尼等其他阻尼时,因阻尼比是无量纲参数,可直接与计算所得的干摩擦阻尼相加减。
1.2 接触模型
接触模型刻画了接触面接触作用力(即切向的摩擦力和法向的正压力)与接触面相对位移的关系,这与系统的摩擦耗能直接相关。本文采用接触节点对进行接触建模。接触节点间的3维相对运动在接触局部坐标系下可分解为面外的法向运动和面内2个相互垂直方向的运动。
经典的库伦摩擦模型假定接触面存在粘滞和滑移2种状态,且二者间瞬时转变,如图2所示。1D切向相对位移-恒正压力接触模型(如图3所示)将接触面的干摩擦等效为线性弹簧与经典库伦摩擦副的串联,并假设法向的正压力恒定,只考虑接触面内1个切向的相对运动。在此基础上,1D切向相对位移-变正压力接触模型(如图4所示)考虑了法向正压力的变化。2D切向相对位移-恒正压力接触模型(如图5所示)考虑了接触面内2个切向的相对运动,而2D切向相对位移-变正压力接触模型(如图6所示)在此基
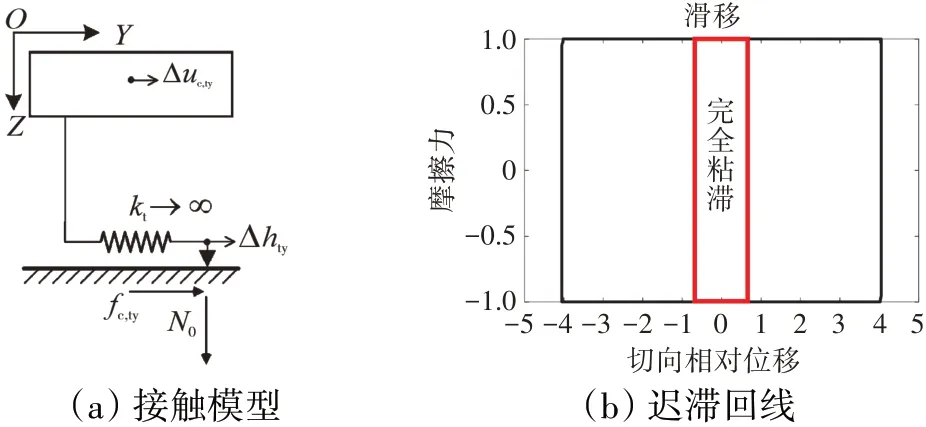
图2 库伦摩擦模型
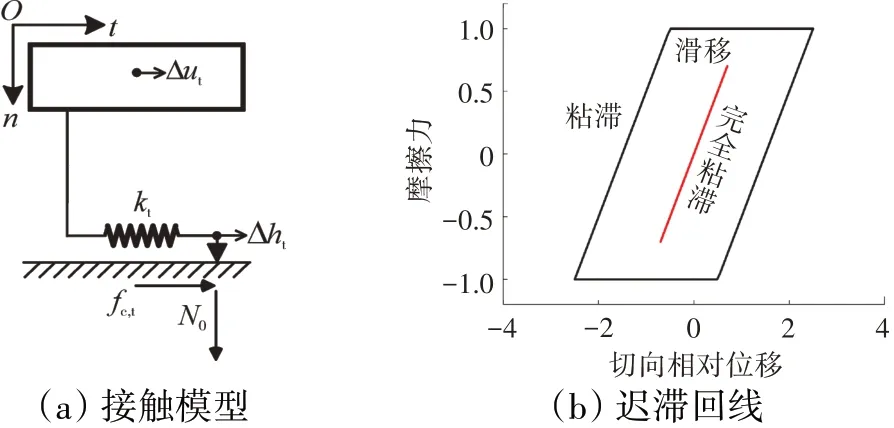
图3 1D切向相对位移-恒正压力接触模型
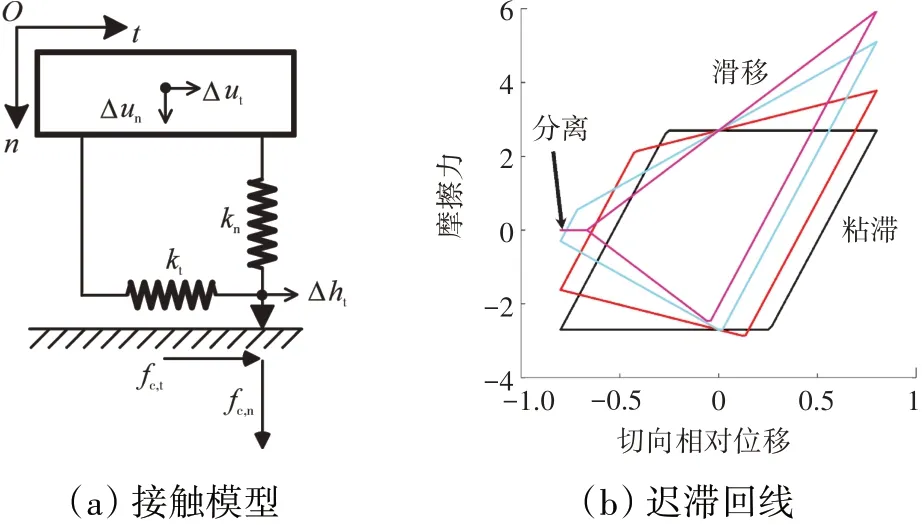
图4 1D切向相对位移-变正压力接触模型

图5 2D切向相对位移-恒正压力接触模型

图6 2D切向相对位移-变正压力接触模型
础上,考虑了法向正压力的变化,被称为全3D接触模型。前述接触模型及其不同接触状态(粘滞、滑移、分离)的转换准则详见文献[9],这里给出全3D接触模型时域内接触作用力的表达式。给定接触节点对之间的相对位移Δuc,tx、Δuc,ty、Δuc,nz,利用接触相对位移Δhtx、Δhty,则法向正压力为


在实际程序计算中采用预报-校正格式,按离散时间步推进迭代求解摩擦力。从上一时刻开始,按照接触规律求解摩擦力后进行下一时刻的求解,直至摩擦力稳定。通常需要几个振动周期迟滞回线便可收敛。
式中:
2 阻尼特性曲线
2.1 摩擦耗能
干摩擦阻尼减振的机理是接触面之间相对运动产生摩擦力,从而耗散振动动能。从能量的角度出发,摩擦耗能与系统振动能量之比可以用来评价阻尼效应。选用合适的接触模型,1个振动周期内摩擦耗能可由接触模型中的迟滞回线所围成的面积得到,即

损耗因子通常被用来评定工程材料的阻尼效果[19],可表达为每个振动周期的耗散能量占系统振动能量的比例,即
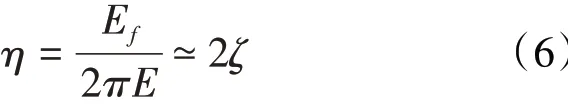
系统振动能量可用1个周期内的最大振动动能Ek来表示,则减振结构(阻尼器)所能提供的等效阻尼比可近似表达为

2.2 等效阻尼比
针对薄壁结构某一阶模态,在小振幅条件下,模态的位移Aref、振动应力σref和最大振动动能Ek,ref和实际的位移A、振动应力σ、最大振动动能Ek间有如下关系

给定考核点某一振动应力σ,计算位移A和最大振动动能Ek;再选取相应的接触模型,可得到相应的摩擦耗能Ef,进而利用式(7)计算当前振动应力下的等效阻尼比ζ;改变振动应力大小,可得到阻尼比随振动应力的变化曲线,即阻尼特性曲线。薄壁结构阻尼特性计算流程如图7所示。值得注意的是,对于不同的减振结构,摩擦耗能的计算方式有差别,这将在下文中予以介绍。
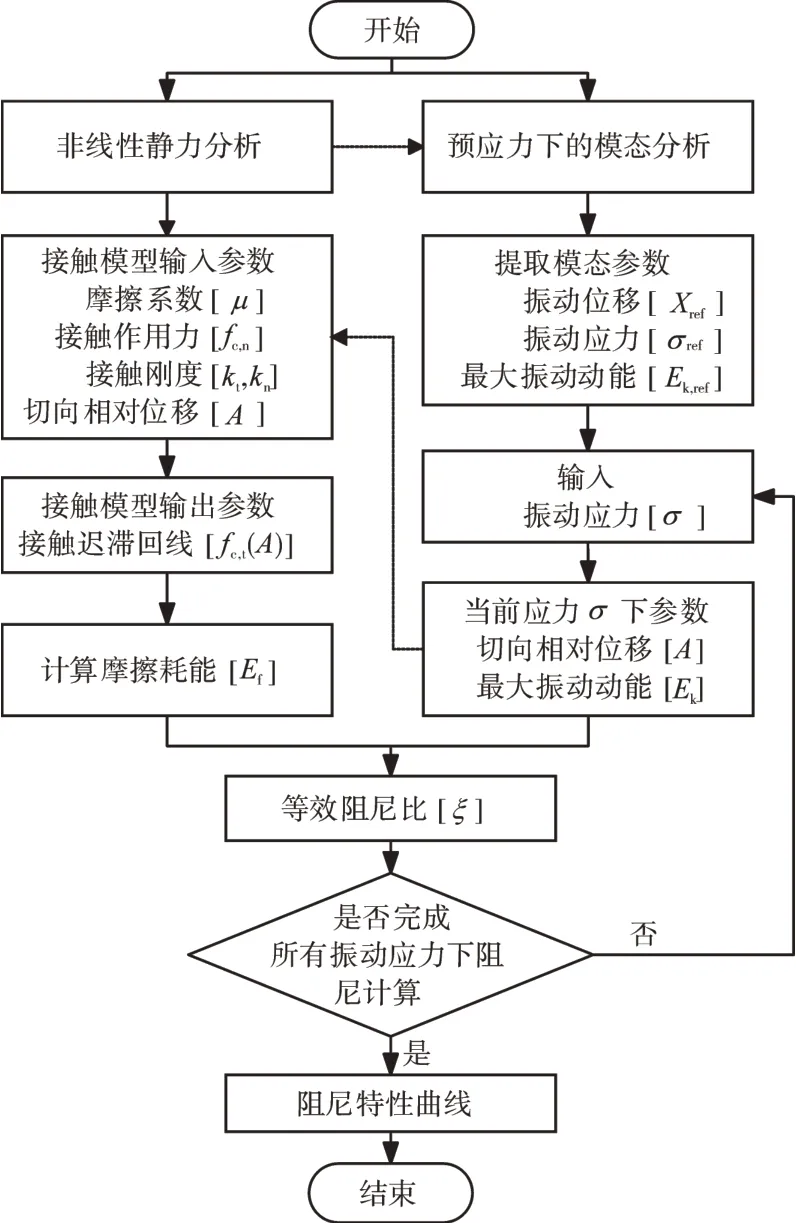
图7 薄壁结构阻尼特性计算流程
3 减振设计分析
3.1 设计分析流程
本文利用阻尼特性曲线进行减振设计,阻尼特性曲线即系统所能提供的阻尼比随结构振动应力的变化曲线,如图8所示。其中,减振结构开始提供阻尼效应时结构考核点的共振振动应力,称为临界振动应力σcr;峰值阻尼比ζmax为阻尼比最大值,其对应的振动应力为σm。干摩擦阻尼减振结构设计分析流程如图9所示。

图8 阻尼特性曲线

图9 干摩擦阻尼减振结构设计分析流程
薄壁结构典型工作状态的稳态应力和许用振动应力范围在设计中往往是已知的,调整减振结构设计参数,以满足阻尼比要求:在许用振动应力下,减振结构能提供尽可能大的阻尼比,即峰值阻尼比尽可能大;同时,临界振动应力要相对小;主结构的典型振动应力落在阻尼特性曲线左半支为最佳,使得振动应力增大时,减振结构提供的阻尼比也随之增大。另外,若需得到某假设激励幅值fe下结构的响
应,则可利用该激励下阻尼比-振动应力曲线与减振结构阻尼特性曲线的交点来获得。
3.2 缘板阻尼器分析示例
缘板阻尼器常用于风扇和高压涡轮转子叶片,典型的结构形式有楔形、柱状、带状及非对称形状等。本例针对涡轮叶盘结构模型(如图10所示),利用其Campbell图分析确定的危险模态(4节径叶片1弯),选取平板式缘板阻尼器按流程进行减振分析。

图10 涡轮叶/盘转子结构有限元模型
相邻叶片振动相位差φ由节径数Nd和叶片数nsec表示为

利用谐波平衡法和B-B(Blade-to-Blade)型接触运动,阻尼器振动位移为v=(uL+uR)/2。阻尼器与缘板间接触左、右面的位移及阻尼器与左缘板相对位移表达为

则接触面相对位移幅值Aref用左、右缘板绝对位移AL、AR表示为

因工作过程中缘板阻尼器由离心力紧压在叶片缘板处,可忽略法向正压力的变化。采用1D切向相对位移-恒正压力接触宏滑动模型(图3),利用式(5)计算摩擦耗能,即

式中:Acr=μN0/kt,为接触面处于粘滞与滑移之间的临界状态时的相对位移。

扇区最大振动动能Ek,ref为式中:Ek,wh为模态分析全环的最大振动动能;Ai为第i扇区的模态位移(驻波模态振幅)。
通过叶盘结构的接触分析和循环对称模态分析,按上述方法获得缘板阻尼器减振参数,见表1。经式(7)计算得阻尼器与单侧缘板摩擦提供的等效阻尼比;需要注意的是,阻尼器与两侧缘板都进行摩擦耗能,最终阻尼比是单侧的2倍。缘板阻尼器不同质量m0下的阻尼特性曲线如图11所示。取许用振动应力50 MPa,则质量为1.2 g时的阻尼效果最佳。
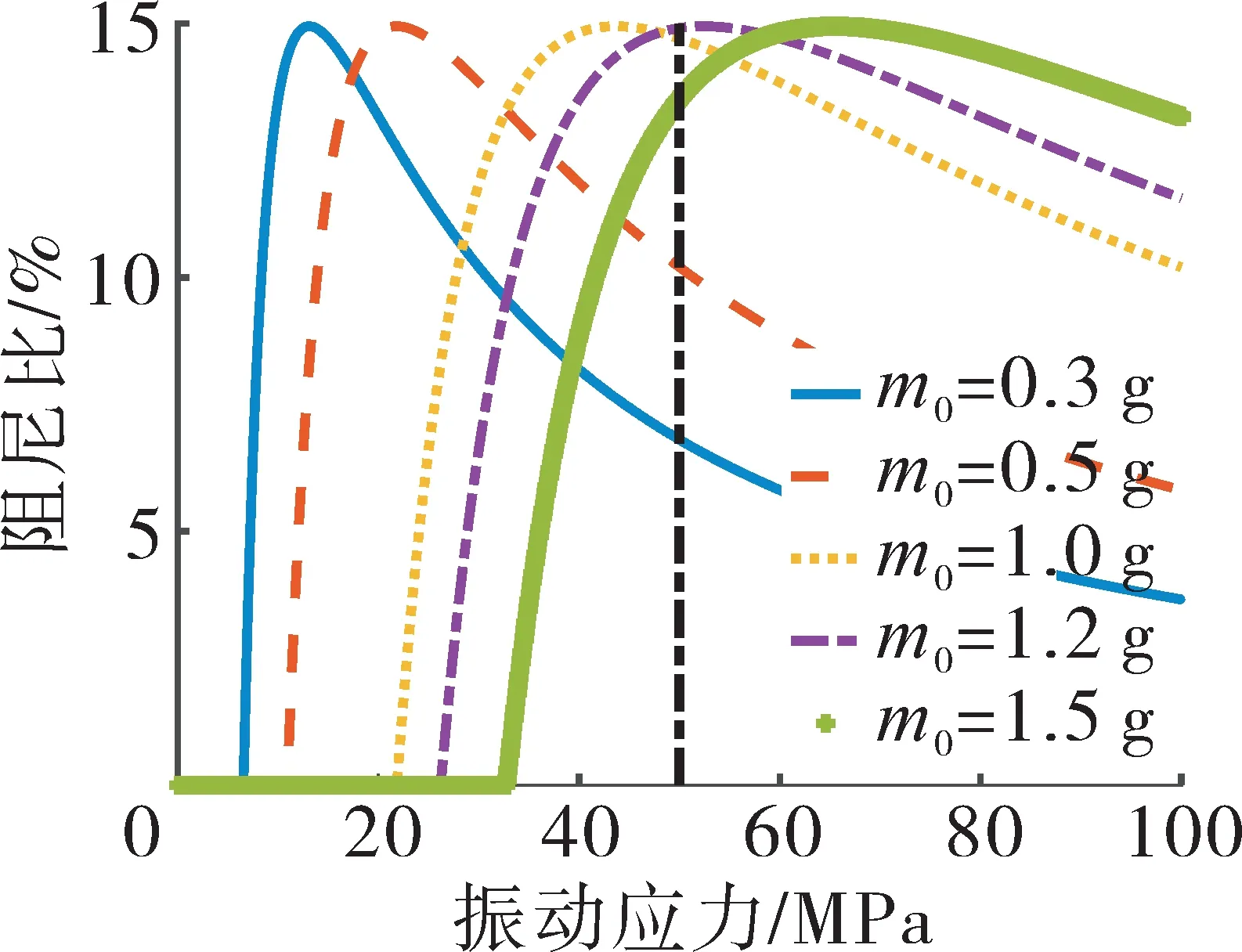
图11 涡轮叶片不同质量缘板阻尼器的阻尼特性曲线

表1 缘板阻尼器减振参数
3.3 叶冠减振分析示例
叶冠主要用于低压涡轮转子叶片,有锯齿冠和平行冠等形式。某锯齿冠叶片结构有限元模型如图12所示。关注危险模态(20节径叶片1弯),选取不同预扭角α对锯齿冠按流程进行减振分析。值得注意的是,叶冠对叶片固有振动特性有较大影响,通过在冠间建立弹簧单元,采用循环对称边界条件,以模拟接触刚度对结构固有振动特性的影响。

图12 某锯齿冠叶片结构有限元模型(经变形处理)
考虑相邻叶片振动相位差φ,锯齿冠接触左、右面的位移及相对位移表达为

相对位移幅值Aref用左、右叶冠绝对位移AL、AR表示为
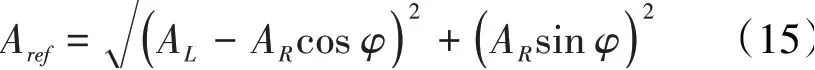
采用1D切向相对位移-恒正压力接触宏滑动模型(图3),利用式(5)、(12)计算摩擦耗能。扇区最大振动动能为Ek,ref。通过接触分析和冠间含等效弹簧(刚度为kn=578 N/mm、kt=289 N/mm)的模态分析,按上述方法获得锯齿冠减振参数,见表2。经式(7)计算得锯齿冠提供的等效阻尼比,锯齿冠不同预扭角α下的阻尼特性曲线如图13所示。取许用振动应力50 MPa,则预扭角为0.5°时的阻尼效果最佳。
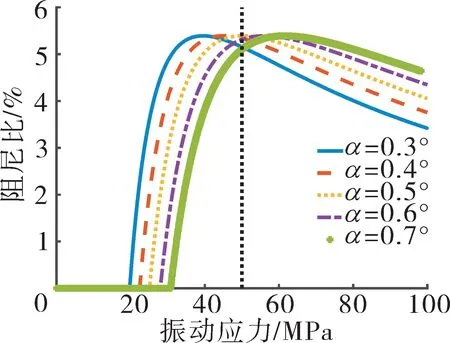
图13 涡轮叶片锯齿冠不同预扭角下的阻尼特性曲线

表2 锯齿冠减振参数
3.4 阻尼环分析示例
阻尼环可应用于航空发动机篦齿封严、整体叶盘、薄壁齿轮等结构的减振,有闭口、C形和螺旋形等形式,横截面有矩形和圆形等。本例对篦齿封严结构模型(如图14所示),关注危险模态(5节径),选取矩形截面(轴向宽度b,径向厚度h)阻尼环按流程进行减振分析。
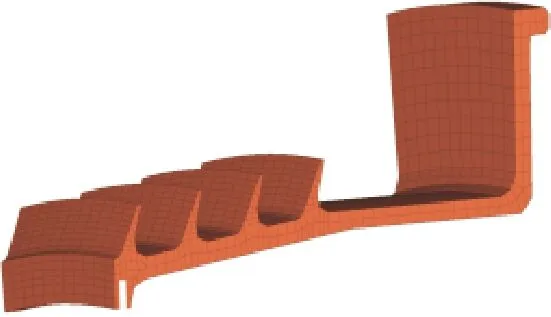
图14 篦齿封严结构有限元模型
与缘板阻尼器、叶冠等结构不同,阻尼环是周向整环连续体,主结构节径型振动的径向分量会导致接触面内的周向变形,进而产生相对位移耗散能量,计算摩擦耗能时采用库伦摩擦模型(图2),通过不同周向位置摩擦力fc,t(θ)与接触面相对位移Δs(θ)乘积的积分获得

式中:P为接触面上单位长度的正压力;Ad为阻尼环横截面面积;E为阻尼环材料弹性模量;Rf为接触面半径;θ0为滑移与粘滞区转换的临界角度
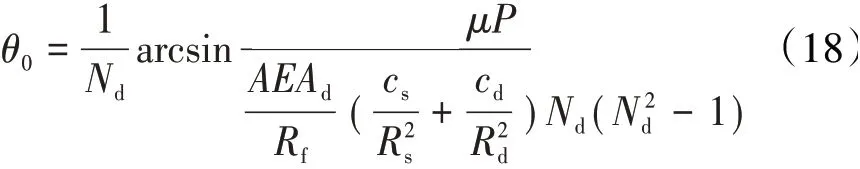
式中:A为篦齿封严结构径向振动位移;cs和cd分别为篦齿环和阻尼环径向半厚度;Rs和Rd分别为篦齿环和阻尼环中性层半径。
提取篦齿封严结构最大振动动能Ek,ref,按上述方法获得阻尼环减振参数,见表3。经式(7)计算得阻尼环提供的等效阻尼比,阻尼环不同径向厚度h下的阻尼特性曲线如图15所示。阻尼效果随着阻尼环径向厚度的增加而提高,其取值在设计许可的范围内越大越好。
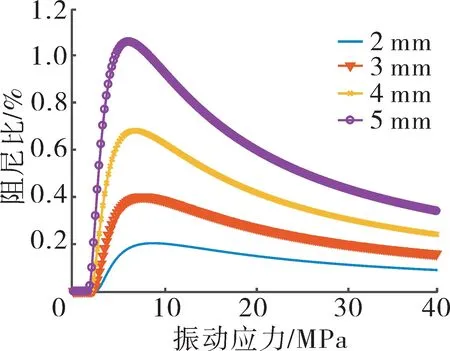
图15 篦齿封严结构阻尼环不同径向厚度下的阻尼特性曲线

表3 阻尼环减振参数
3.5 阻尼套筒分析示例
阻尼套筒可应用于篦齿封严和减涡器引气管等结构的减振,有简单筒状、指状、裂式环等形式。本例针对某减涡器结构模型(如图16所示),关注引气管2弯危险模态,选取安装于引气管内部的裂式阻尼套筒按流程进行减振分析。接触面相对运动及摩擦耗能在引气管轴向为x向、引气管周向为θ向的局部坐标系进行分析。主结构弯曲振动时会导致接触面内沿引气管轴向的变形,进而产生轴向相对位移耗散能量,计算摩擦耗能时采用库伦摩擦模型(图2),通过不同位置摩擦力fc,t(x,θ)与接触面相对位移Δs(x,θ)乘积的积分获得

图16 减涡器及阻尼套筒有限元模型

式中:cs和cd分别为引气管壁半厚度和阻尼套筒壁半厚度;A为引气管径向振动位移;L为阻尼套筒轴向长度;a、b、c、d为用于刻画主结构振型函数的4个系数(可由有限元模态分析结果拟合得到);Rf为接触面半径;x0为滑移与粘滞区转换的临界轴向位置,满足
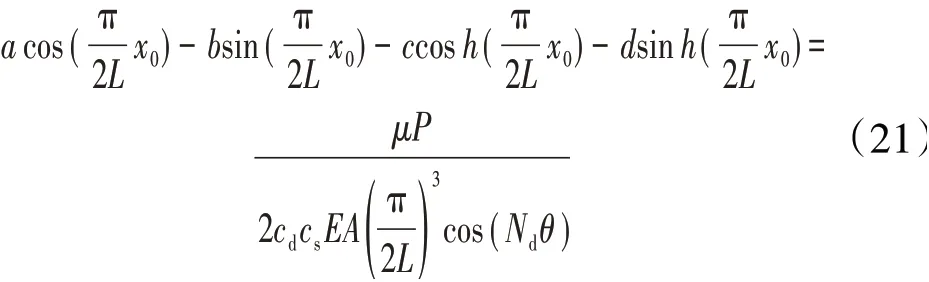
需要注意式(21)为超越方程,可用数值方法求解。
经式(7)计算得阻尼环提供的等效阻尼比,阻尼套筒不同轴向长度L下的阻尼特性曲线如图17所示。从图中可见,阻尼效果随着阻尼套筒轴向长度的增加而提高,其取值在设计许可的范围内越大越好。提取引气管结构最大振动动能Ek,ref,按上述方法确定阻尼套筒减振参数,见表4。

图17 减涡器阻尼套筒不同长度下的阻尼特性曲线

表4 阻尼套筒减振参数
4 结论
(1)阻尼特性曲线可用于评定减振结构提供的阻尼比,给出了在所关注模态下阻尼比随主结构考核点振动应力的变化关系。
(2)对分析的涡轮叶片模型缘板阻尼器质量进行减振设计,取许用振动应力50 MPa,质量为1.2 g时的阻尼效果最佳。
(3)对分析的涡轮叶片锯齿冠预扭角进行减振设计,取许用振动应力50 MPa,预扭角为0.5°时的阻尼效果最佳。
(4)对分析的篦齿封严结构进行阻尼环减振设计,阻尼环径向厚度越大,阻尼效果越好,可在设计许可范围内取大值。
(5)对分析的减涡器引气管所用裂式阻尼套筒,套筒长度的增加有益于阻尼效果的提高。
需要指出的是,本文方法及其流程针对的是模态非密集结构的单一模态进行的减振分析,后续需要综合考虑多个模态,尤其模态密集的结构,进一步发展其减振设计分析方法。
