叶轮机气弹耦合方程求解的时间推进方法评估

曹琳婷，王丁喜，黄秀全

（西北工业大学动力与能源学院，西安 710129）

0 引言

流体和固体之间的耦合作用（Fluid Structure Interaction，FSI）普遍存在于航空航天、海洋、建筑和生物等工程研究和应用领域。在叶轮机研究领域，流固耦合作用产生的气动弹性振动问题对结构的潜在破坏性极大，严重时会造成重大经济损失。在叶轮机流固耦合诱发的振动问题中，根据激励的来源，可以将振动分为自激振动和强迫响应[1]。其中颤振是自激振动的典型代表。为了预防颤振或强迫振动的发生，高效率和高精度的流固耦合技术在航空发动机设计中的应用不可或缺。

定量的压气机气弹性能分析不可避免地需要求解流动控制方程和结构控制方程，其中时间推进的耦合求解方法在多排错频设计以及叶片动响应分析等方面仍有解耦分析不具备的优势。基于计算流体力学（Computational Fluid Dynamics，CFD）和计算结构动力学（Computational Structural Dynamics，CSD）耦合的时域数值分析方法可以分为直接求解原始结构动力学方程的流固全耦合法[2]和求解降阶结构动力学方程的流固部分耦合法[3]。前者非常复杂，通常需要消耗大量计算资源，其工程应用非常少；后者常用于学术研究和工程设计中，因此有大量的研究着重于提高部分耦合法计算的精度和效率。

流固部分耦合法早在2维叶栅的颤振分析中就得到了应用，相似的研究[4]都将结构动力学方程降阶为平动和旋转2个自由度，在这个基础上采用伪时间迭代使得耦合更加紧密，其流场和结构的真实时间推进都采用显式龙格-库塔格式。Sadeghi等[6]为解决3维气动弹性问题给出了一种基于2阶向后差分的双时间步长法的时间推进方法，并应用于机翼颤振的预测；Bendiksen等[7]较早地提出了将Newmark-β、Wilson-θ等一系列常见于结构动力学方程求解的单步法用于气动弹性方程的时域推进，同时也提到关于Adams及其他线性多步法，Adams线性多步法是现代数值计算中的一类重要方法，适用于求解包含复杂函数的常微分方程；Robinson等[8]将基于Adams-Moulton的预测-校正方法用于气动弹性方程的时域推进；蒋跃文等[9]利用标准气动弹性模型校验了6种Adams相关格式时间推进的精度和稳定性，并提出了一种流场迭代次数少并且稳定性好的半隐式线性多步法；Dokainish等[10]整理并对比了求解单自由度结构动力学方程的各类时间推进方法，分析了各方法的计算特性。但在多数涉及叶轮机流固耦合的时间推进方法研究的公开文献中，研究者侧重于发展新的时间推进格式，而对不同时间推进格式的效率对比研究较少。

为填补了上述研究领域的空缺，本文通过对比不同时间推进方法的计算效率，力求找到求解流固耦合气弹方程的最佳方法。

1 气弹控制方程的求解

1.1 流场控制方程

流场控制方程采用圆柱坐标系下的Unsteady Reynolds-averaged Navier-Stokes（URANS）方程

式中：Q为守恒变量；F、G、H分别为轴向、周向和径向的对流通量；Qvg,x、Qvg,θ、Qvg,r分别为对应3个坐标方向的由于网格运动引起的通量；Vx、Vθ、Vr分别为对应3个坐标方向的粘性通量；S为源项。

对该方程的详细解释见文献[11-12]。另外，采用Spalart-Allmaras湍流模型[15]来封闭方程，此处不再赘述。

1.2 结构控制方程

结构控制方程的推导基于牛顿第2运动定律，其矩阵表达式为

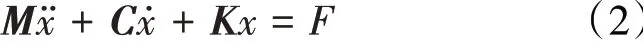
式中：从左至右第1项为惯性力；第2项为摩擦力；第3项为弹性力；第4项为气动力F；M为质量矩阵；C为摩擦系数矩阵；K为刚度矩阵；x为位移向量。

叶轮机叶片小展弦比和实心的特点决定其振动固有频率高，因此流固耦合对叶片振动振型的影响小，从而使得在流固耦合数值分析中可以忽略其振型由于流固耦合的影响而引起的变化。叶片固有振型/频率就是其在真空中振动的振型，因此在无气动力和阻尼力的真空条件下，式（2）可写为

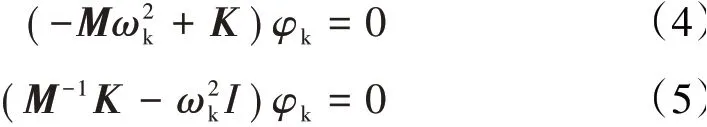
根据模态分析得到的模态向量为φi（叶片的振动模态），模态向量还满足正交性

叶片振动的位移向量可以由模态向量φi的线性组合表示

式中：N为结构动力学方程的维度，也是叶片振动的自由度；qi为标量。

将式（7）的位移表达式代入式（2），可得到

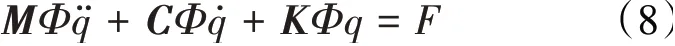
再将上述方程左右同乘振型矩阵的共轭转置ΦH得到

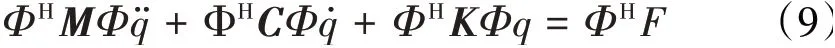
再根据振型的正交特性，上述方程的左端质量矩阵、摩擦系数矩阵和刚度矩阵分别被对角化为

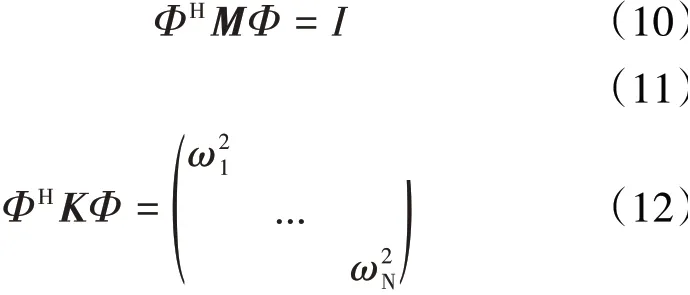
于是式（2）降阶为N个独立的标量方程

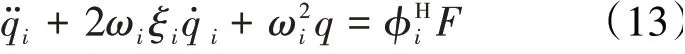
上述方程的右端项称作模态力，通过URANS方程求解得到。此时，气弹控制方程（2）的数值求解简化成了单自由度方程（13）的求解问题。

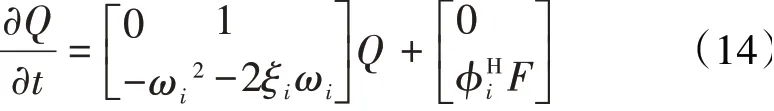
2 时间推进方法

流固耦合系统的气弹控制方程中的结构动力学方程可以用常微分方程(14)的形式表达，其右边项可以改写为

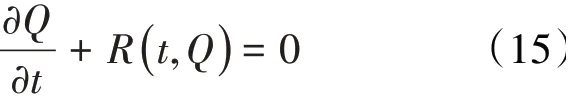
方程(15)的时间导数项可采用不同的离散格式以达到时间推进的目的，本文选取以下几种经典格式进行比较。

1阶显式欧拉（1EEM）

1阶隐式欧拉（1IEM）

1阶混合欧拉（1HEM）

4阶显式Adams（4EAM）

4阶隐式Adams（4IAM）

4阶半隐式Adams[18]（4SAM）

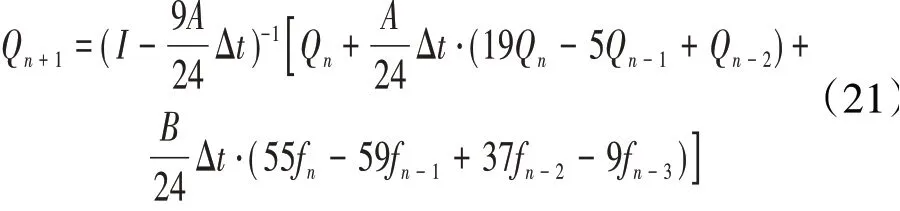
该方法的本质是结构项用4阶隐式Adams格式，气动力项用4阶显式Adams格式离散的混合格式。

基于Adams的预测校正方法（PCAM）

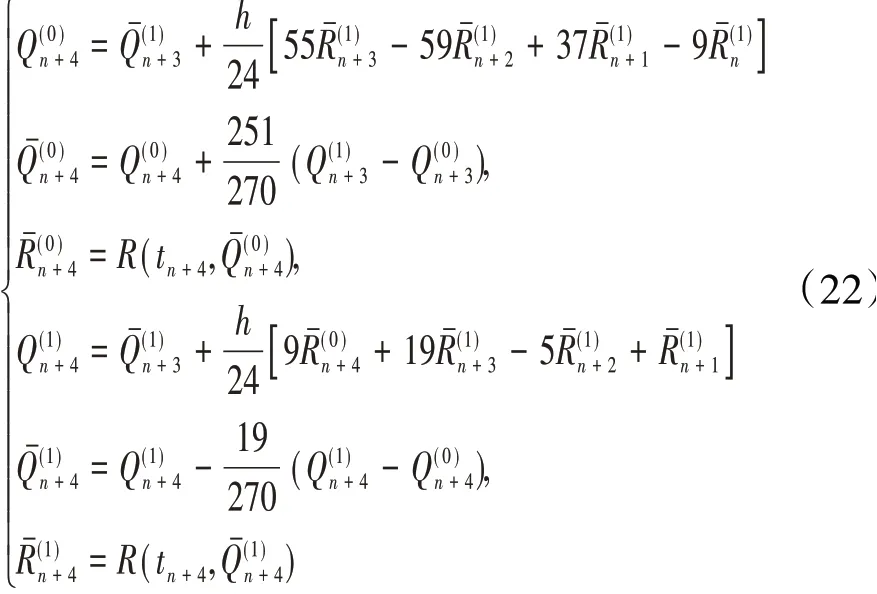
4-1显式龙格-库塔方法（MRK）

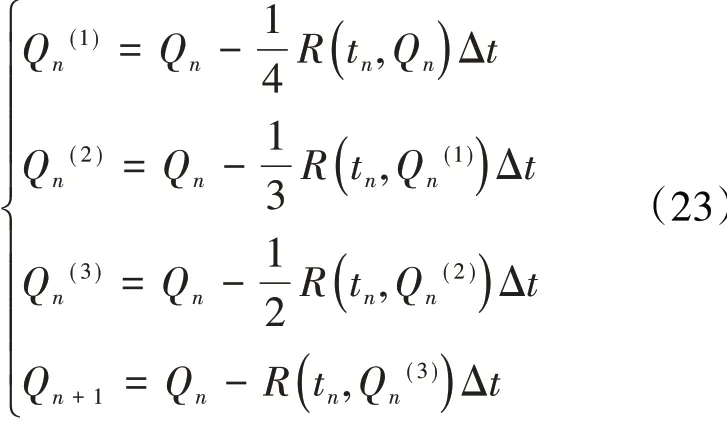
基于2阶向后差分的双时间步长法

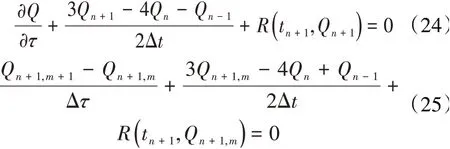
双时间步长法引入了伪时间导数项，并对伪时间导数项差分得到内迭代的形式(25)。为了获得时间精确解，在每个物理时间步内需要进行多次内迭代，迭代次数选取为10～20次[16]。

经典龙格-库塔方法（Classical Runge-Kutta）的推进格式为

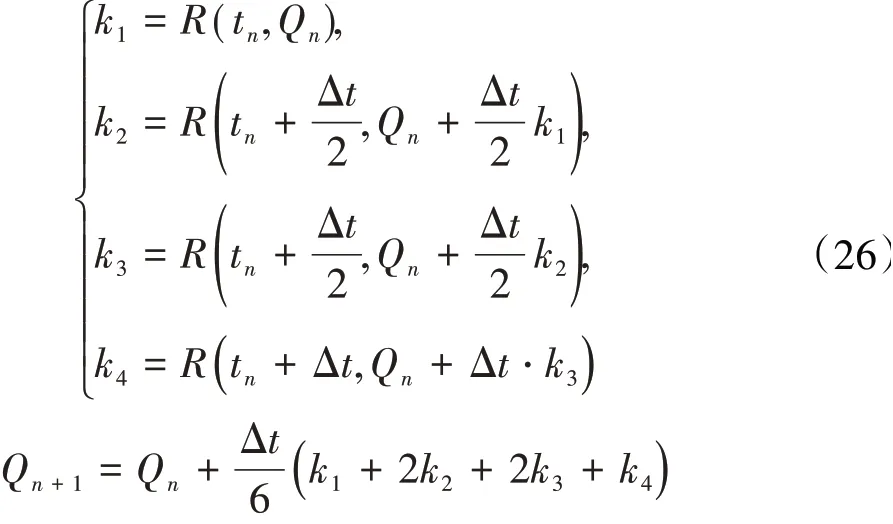
采用式（26）的时间推进方法求解气弹方程中的R(tn,Qn)时，每步需要具备3个时刻点tn、tn+Δt/2、tn+Δt的流场求解信息，传统的简化处理方式是将气动力项在每个时间步内冻结。这种处理方式会导致计算精度大大降低。本文发展了一种算法可以避免这一问题。经典龙格-库塔应用于气弹方程求解的算法如图1所示。以原先的Δt/2为时间步长，结构控制方程第n步的求解需要的3个流场时刻点为第n步、第n-1步、第n-2步，流场控制方程第n步的求解需要的结构时刻点为第n-2步，推进格式可以重新写为

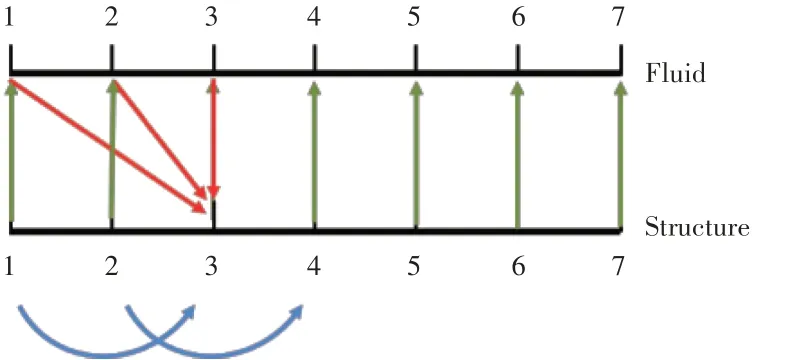
图1 经典龙格-库塔应用于气弹方程求解的算法

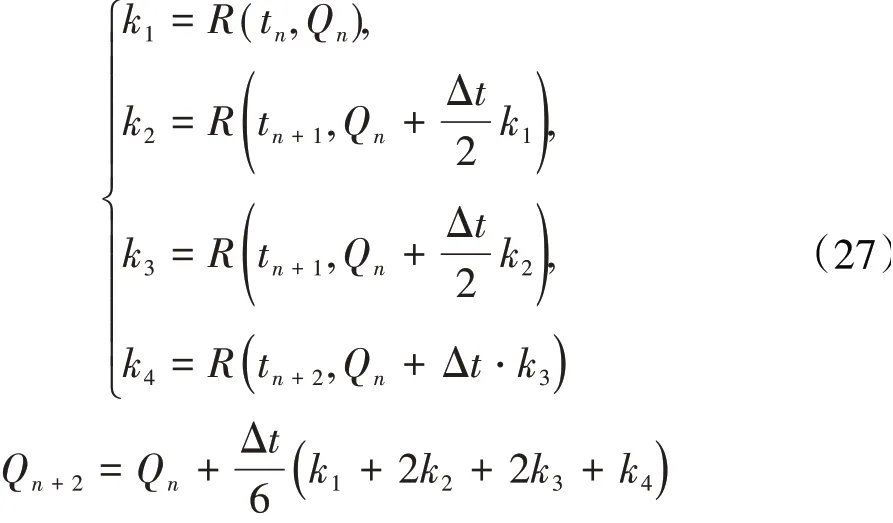
Newmark方法本身可以直接求解2阶常微分方程（例如结构动力学方程(2)），相比其他方法省略了将2阶方程转换成1阶的步骤。该方法的求解迭代过程为

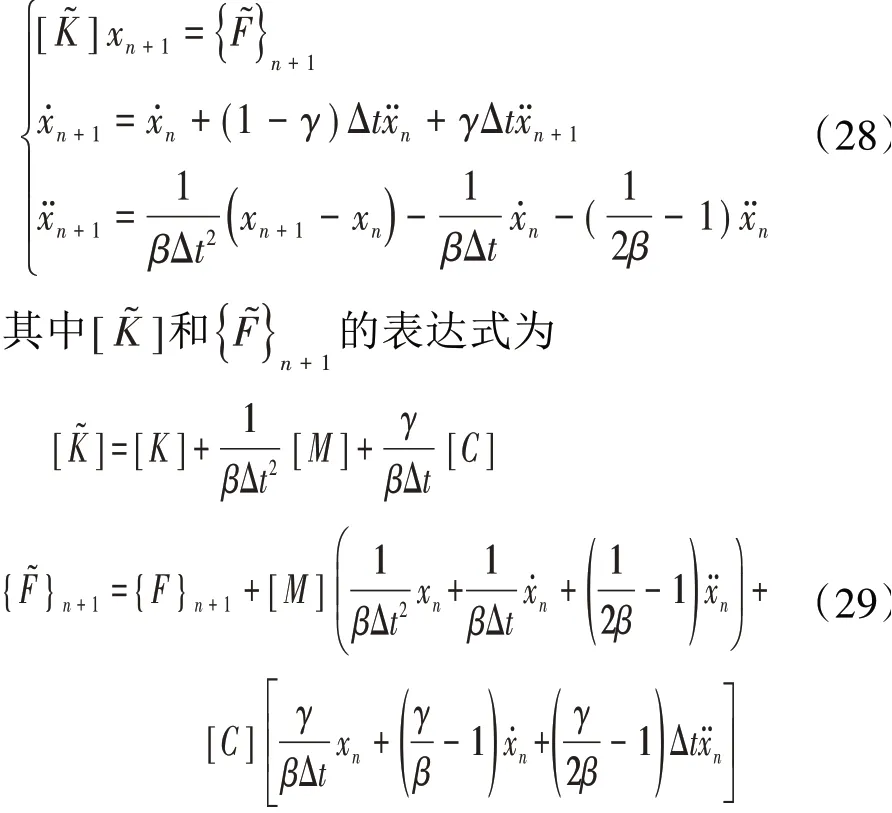
尽管计算过程复杂，但在γ=0.5、β=0.25时，Newmark方法具有2阶精度以及无条件稳定的优势，因此也常用于工程计算。

3 结果比较与分析

3.1 单自由度弹簧系统

为了比较上述时间推进方法的效率和精度，采用2个算例进行验证。第1个算例是单自由度有阻尼的弹簧-质量系统，其受迫振动可以用2阶线性常系数微分方程描述

该方程和降阶结构动力学方程(13)具有相同的形式，不同仅在于右边项f。假设f是简谐力，A为简谐力的振幅，ωex为简谐力的频率，运动方程(30)具有理论解

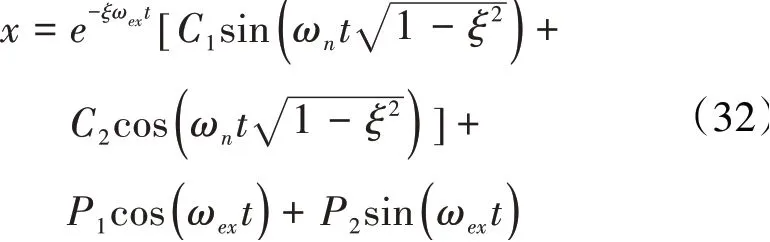
式中：C1、C2、P1和P2分别为常系数。

通过上节提及的时间推进方法求出数值解，该模型方程的数值解与理论解的误差用2-范数定义

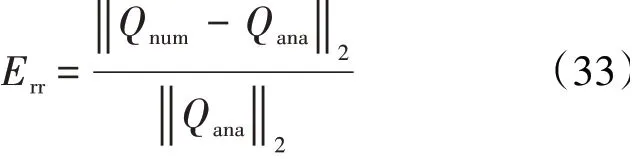
式中：Qnum和Qana分别为方程的数值解和理论解。

在每个振动周期分别划分了10、20、50、100、200、500、1000个时间步来考察时间步长与相对误差的关系。在总时长45个振动周期内各时间推进方法的相对误差与时间步长的关系如图2所示。横纵坐标均采用对数形式，但该图横坐标的刻度标注为单个振动周期内的时间步数。

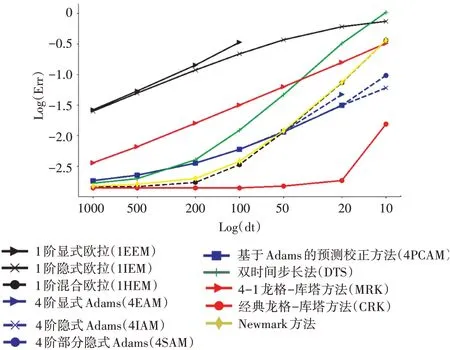
图2 各时间推进方法数值解的相对误差与时间步长的关系

从图中可见，显式方法的稳定性较差，如1阶显式欧拉每个振动周期需要100个时间步以上才能收敛；1阶混合格式、Newmark以及双时间步长法同是2阶精度方法，其准确性对时间步长大小非常敏感，减小时间步长使误差减小的效果显著；基于4阶Adams方法的4种方法都有着极为接近的误差-时间步长关联曲线，其中隐式Adams在较大时间步长（20～50个时间步）略具优势；4-1龙格-库塔方法与经典龙格-库塔方法的差距很大，原因是伴随着方程右项外力f的计算次数减少，4-1龙格-库塔的准确度也大大降低；在考查的所有方法之中，经典龙格-库塔方法的精度和效率最高。

3.2 颤振分析

由于压气机结构比单自由度弹簧系统复杂得多，这些时间推进方法在压气机叶片颤振耦合分析中的适用性需要专门研究。另外，区别于单自由度弹簧系统，时域耦合模拟的流场气动力是未知的。这需要求解URANS方程和结构动力学方程时交替迭代，因此会对各项时间推进方法的准确度产生一定影响。

颤振分析的算例选取跨声速风扇转子NASA Rotor 67[17]，此算例存在相对翔实的试验数据，因此被广泛用于数值分析结果的校验，也常被用于颤振研究[18-20]。采用单通道计算域，计算网格周向41个网格点，径向89个网格点，轴向161个网格点。跨声速转子NASA Rotor 67颤振计算网格如图3所示。进行颤振分析时选取前2阶振型作为考查对象：1阶弯曲振型（584.04 Hz）和1阶扭转振型（1256.95 Hz）。

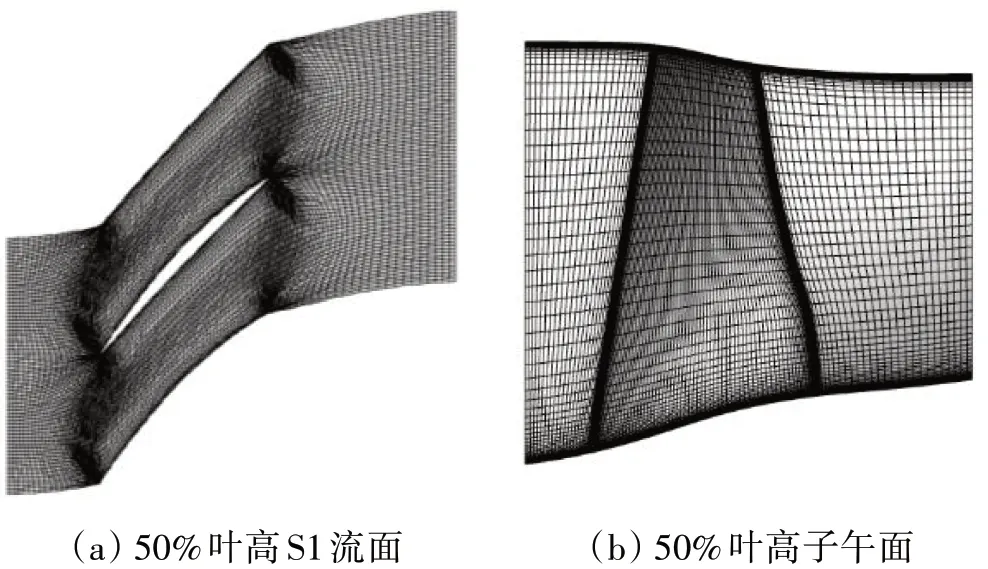
图3 跨声速转子NASA Rotor 67颤振计算网格

以双时间步长法为例，当时间步长取5.68×10-6s时，计算完成了10000步迭代，等效于叶片的1阶模态振动了33个周期，2阶模态振动了71个周期，其模态位移如图4所示。展示了1阶和2阶模态的模态位移随迭代步数的演化。根据峰值的衰减速度可以确定叶片振动的对数衰减率δ（Log-Dec）

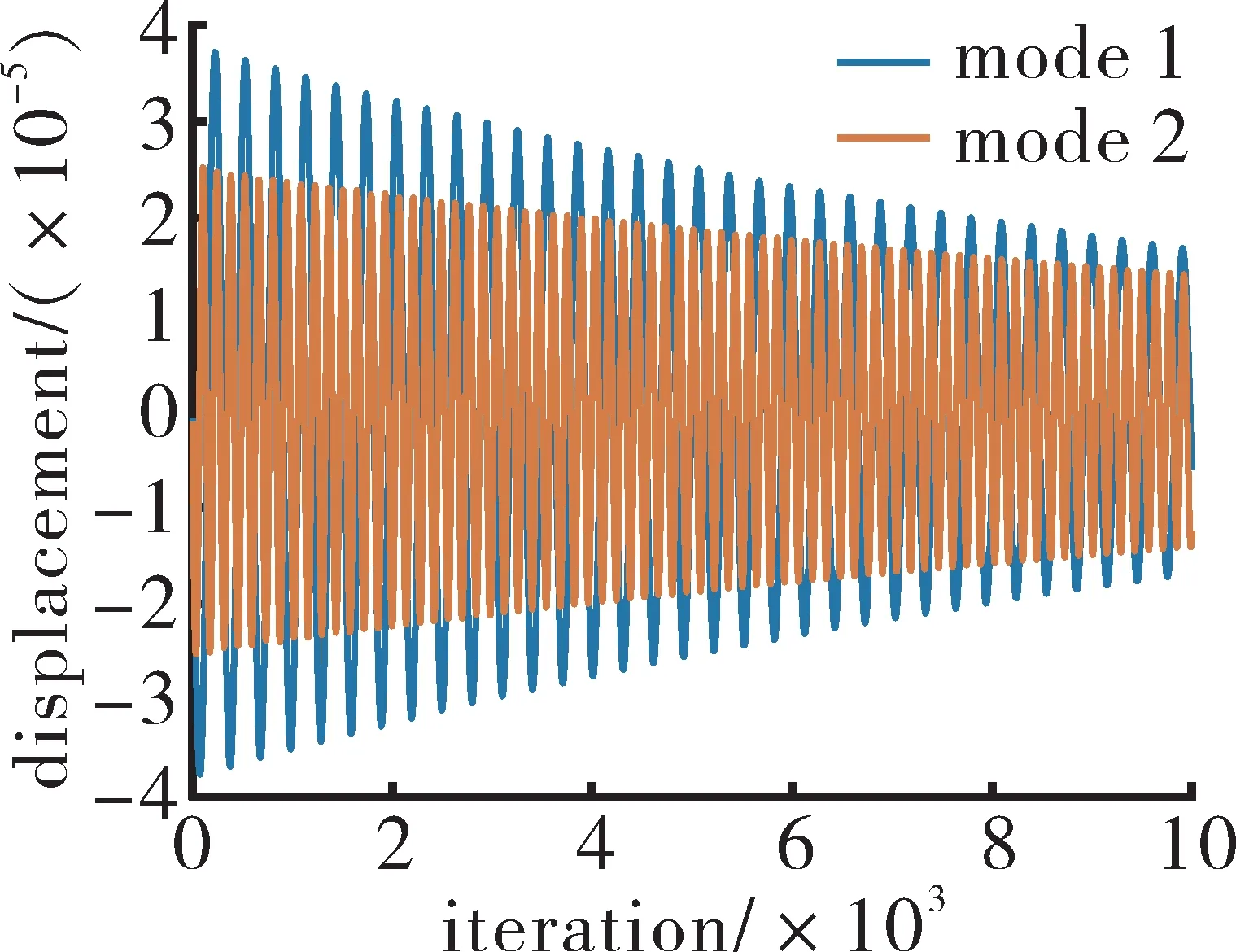
图4 双时间步长法在时间步长为5.68×10-6 s时迭代10000步的模态位移

式中：W为积累功；Estrain为振动叶片的应变能。

由于模态位移相邻2个峰值之间的时间步较少，依据其计算对数衰减率时不可避免地带来较大的数值误差，计算得到的对数衰减率δ出现幅度较大的振荡。为了减小数值误差的影响，计算对数衰减率δ

本文将δ作为颤振计算时间步长不相关的考察对象，将ci作为评估时间步长不相关的指标。c1和c2的下标分别代表1阶和2阶模态。若有这样的Δt能满足式(36)，则说明颤振计算满足时间步长不相关条件，其中max(Δt)是允许范围内的最大时间步长。在式(36)中，Δτ固定为1个足够小的时间步长（2.84×10-6s）。在固定时间步长为Δτ时各时间推进方法的对数衰减率如图5所示。从图中可见，在时间步长足够小时，各方法的对数衰减率结果是相吻合的。对所有出现在图5中的时间推进方法，Δτ对应的对数衰减率计算已经达到时间步长不相关，因此可以作为参考标准。

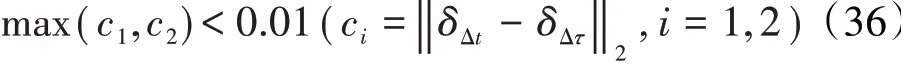
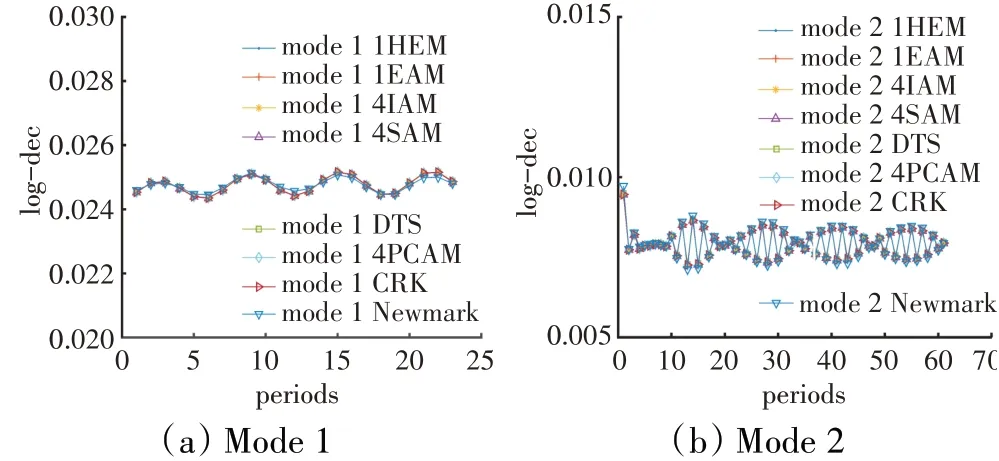
图5 在固定时间步长Δτ（2.84×10-6 s）时各时间推进方法的对数衰减率

各时间推进方法的最大时间步长如图6所示，图中的纵坐标Δt以Δτ的倍数衡量。从图中可见，经典龙格-库塔方法的最大时间步长为6.7倍的Δτ（1.89×10-5s）；其次是4阶隐式Adams方法和Newmark方法，最大时间步长为（5.70~6.25）Δτ，即（1.62~1.78）×10-5s；1阶混合欧拉、4阶 显式Adams、4阶部分隐式Adams以及基于4阶Adams的预测校正方法的最大时间步长均为（3.6~4.0）Δτ，即（1.03~1.14）×10-5s；双时间步长法的最大时间步长为2Δτ，即5.68×10-6s。

图6 各时间推进方法的最大时间步长

对于1阶显式欧拉和1阶隐式欧拉，前者在时间步长取值很小时（＜Δτ）颤振计算结果仍发散；后者在时间步长取值很小时（＜0.4Δτ）计算与时间步长仍相关。另外，4-1龙格-库塔方法类似于1阶隐式欧拉，时间步长取值在＜0.4Δτ时的颤振计算仍与时间步长相关。鉴于本文的研究目的是找寻效率最高的时间推进方法，因此上述3种方法均不纳入考虑范围。在所有考虑的时间推进方法中，Newmark方法和基于4阶Adams的预测校正方法增加了全局变量的存储单元，但凭借如今计算技术的发展，足以忽略这些新增存储单元带来的负担。

分析上述结果可知，max(Δt)越大，代表计算时需要耗费的迭代次数越少。因此，经典龙格-库塔方法是所有时间推进方法中最节省计算时间成本的方法。4阶显式Adams、部分隐式Adams和预测校正方法的最大时间步长十分接近。在所有纳入考虑的方法中，双时间步长法的最大时间步长是最小的，计算耗时最多。这些结论也与前述单自由度弹簧系统的相关数值计算结论相符合。

上述结论和单自由度弹簧系统得出结论不同之处在于，求解单自由度弹簧系统得出的结论是Newmark方法略逊于1阶混合欧拉格式，但是在颤振耦合计算时Newmark方法表现更佳，并且其优越性仅次于经典龙格-库塔的。原因可能在于流固耦合问题的流场方程求解是与结构方程求解交替进行的，1阶混合欧拉格式采取显隐式混合来计算模态力，而Newmark方法则采取的是隐式，减少了流场求解结果的数值损耗。同理也可以解释4阶隐式Adams方法在颤振耦合计算时比其余3种结果相似的Adams方法更佳。

4 结论

（1）2项研究的计算结果有很多共同点，说明时间推进方法的效率更多地与方法本身的数学性质有关。因此对于复杂的流固耦合问题，研究不同时间推进方法的准确性和耗时成本可以参考简单模型的。但是流固耦合求解时流场和结构的信息交互可能带来一定影响，因此还需要校验；

（2）在所有考查的时间推进方法中，经典龙格-库塔方法的计算效率最高，稳定性好；其次是Newmark和4阶隐式Adams方法；基于2阶向后差分的双时间步长法效率最低；

（3）流固耦合求解过程中流场部分的求解难度和耗时远大于结构部分，因此选用时间推进方法时应不吝惜耦合难度和内存占用的缺点，选择稳定性更好的隐式方法。