double-order Hilfer分数阶共振边值问题解的存在性
2022-11-28孟凡猛江卫华郭春静
孟凡猛,江卫华,郭春静
(河北科技大学理学院,河北石家庄 050018)
分数阶微分方程广泛用于解决物理、化学、经济等学科的实际问题[1-5]。边值问题研究起源于应用数学和物理领域[6-8],弹力稳定性理论中很多问题都可以采用边值问题方法加以解决。因此,分数阶微分方程边值问题受到很多专家和学者的关注[9-12]。
许多研究者研究了常见的Riemann-Liouville导数和Caputo导数的边值问题。例如,WANG等[13]研究了Riemann-Liouville分数阶微分方程三点边值问题
解的存在性,其中1<α<2,0<ξ<1,ηξα-1=1。将共振边值问题转化为非共振边值问题,再运用不动点定理,可得到Riemann-Liouville分数阶微分方程三点边值问题解的存在性。TANG[14]研究了共振情形下Caputo分数阶微分方程四点边值问题
解的存在性,其中1<α≤2,0<ξ,η<1。运用Mawhin的重合度理论,可得到共振情形下Caputo分数阶微分方程四点边值问题解的存在性。HILFER[15]对Riemann-Liouville导数和Caputo导数进行了推广,得到介于这2个导数之间且包含这2个导数的Hilfer分数阶导数。具有Hilfer导数的分数阶微分方程在近10年取得了一些成果[16-19]。RI等[20]研究了共振情形下Hilfer分数阶微分方程多点边值问题
其中φ1(t),φ2(t)∈C[0,T],ζ0(x)∈C[0,l]。文献详细介绍了广义Hilfer导数的概念,给出了它的拉普拉斯变换公式,讨论了反常扩散方程边值问题的封闭解,但并没有详细说明double-order Hilfer分数阶微分方程边值问题的可解性问题。
目前,研究人员已经对Riemann-Liouville和Caputo分数阶微分方程边值问题的可解性进行了广泛研究。从文献来看,尚未对共振情形下具有double-order Hilfer导数的分数阶微分方程边值问题展开研究。因此,基于前人的研究基础,笔者研究共振条件下double-order Hilfer分数阶微分方程积分边值问题
(1)
1 预备知识
为了方便起见,引入一些符号和定理。
设X,Y是实Banach空间,L:domL⊂X→Y是指数为零的Fredholm算子,P:X→X和Q:Y→Y是连续投影算子,且满足ImP=KerL,KerQ=ImL,X=KerL⊕KerP,Y=ImL⊕ImQ。由此可知,L:domL∩KerP→ImL是可逆的,用Kp表示它的逆。


1)∀(u,λ)∈[(domLKerL)∩∂Ω]×(0,1),Lu≠λNu;
2)∀u∈KerL∩∂Ω,Nu∉ImL;
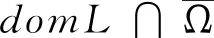
定义2[5]函数y:(0,+∞)→R的α>0阶Riemann-Liouville分数阶积分定义为
其中等号右边是在(0,+∞)上逐点有意义。
定义3[5]函数y:(0,+∞)→R的α>0阶Riemann-Liouville分数阶导数定义为
其中等号右边是在(0,+∞)上逐点有意义,n=[α]+1。
定义4[21]函数y:(0,+∞)→R的α,β阶δ型double-order Hilfer分数阶导数定义为
(2)
其中(m-1)<α 注1[21]: 定义5[5]对任意的0≤η<1,函数y的加权空间定义为 Cη(0,1]:={y|tηy(t)∈C[0,1]}, u(t)=c1tα-1+c2tα-2+…+cntα-n, 其中ci∈R,i=1,2,…,n,n=[α]+1。 引理3[5]如果α>0,β>-1,且β≠α-i,i=1,2,…,[α]+1,那么 引理4[5]如果α>0,β>0,且y∈L1(+),那么 引理5[5]如果α>β>0,且y∈L1(+),那么 特别地,当β=k∈且α>k时,有 引理6[26]在[a,b]上的任一有界变差函数f(x)都可以表示为2个增函数之差,即存在2个增函数h(x)和g(x),使得f(x)=h(x)-g(x)。 设X=Cn-γ(0,1],Y=C[0,1]。 假设以下条件成立。 (H2) 映射f:(0,1]×R→R满足Carathéodory条件:对几乎所有的t∈(0,1],f(t,x)是x的连续函数,对每一个x,f(t,x)是t在(0,1]上的可测函数,并且对∀r>0,存在φr∈Y,满足|f(t,x)|≤φr(t),|x|≤r,a.e.t∈(0,1]。 定义算子L:domL⊂X→Y和算子N:X→Y分别如下: 其中, 引理7设(H1)成立,则L:domL⊂X→Y是一个零指标的Fredholm算子。 证明:显然KerL={u∈domL|u(t)=ctγ-n,∀t∈(0,1],c∈R}。 通过注1可以得到 (3) (4) 因此 综上所述,得到 定义线性算子P:X→X, 显然, X=KerL⊕KerP。 定义线性算子Q:Y→Y, 通过计算得到Q2y=Qy,即Q是一个幂等算子,是Y上的线性投影算子。显然,ImL=KerQ。 任取y∈Y,可写成y=(y-Qy)+Qy,其中(y-Qy)∈KerQ=ImL,Qy∈ImQ,因此Y=ImL+ImQ。取y∈ImL∩ImQ,由y∈ImQ得y=Qy;由y∈ImL=KerQ,得Qy=0,因此y=0,Y=ImL⊕ImQ。又dimKerL=1=codimImL,所以,L是一个零指标的Fredholm算子。 引理8定义线性算子Kp:ImL→domL∩KerP, 则Kp=(L|domL∩KerP)-1。 证明:取y∈ImL,可以得到Kpy∈domL∩KerP,且 另一方面,若u∈domL∩KerP,由引理4和引理5可得: 因此,Kp=(L|domL∩KerP)-1。 |f(t,u(t))|≤φr(t),t∈(0,1]。 |tn-γKp(I-Q)Nu(t)|≤ 定理1假设(H1)和(H2)以及下面的3个条件成立: (H3)存在常数M>0,使得当u∈domL,∀t∈(0,1],|u(t)|>M时,QNu≠0。 (H4)存在非负函数a(t)∈X,b(t)∈Y,使得 |f(t,x)|≤a(t)+b(t)|x|,t∈(0,1],x∈R, (H5)存在常数B>0,如果|c|>B,那么cQNu(t)>0或cQNu(t)<0(其中u(t)=ctγ-n)中有一个不等式成立,边值问题(1)至少有一个解。 为证明该结论,首先证明如下3个引理。 引理10若条件(H3)和(H4)成立,则Ω1={u|u∈domLKerL,Lu=λNu,λ∈(0,1)}在X上是有界的。 证明:任取u∈Ω1,则Lu(t)=λNu(t),因此 依据λNu∈ImL=KerQ,得QNu(t)=0。通过条件(H3)可知,存在t0∈(0,1],使得|u(t0)|≤M。 将t=t0代入u(t)中,得 那么有 因此 整理得 故Ω1是有界的。 引理11若条件(H1)—(H3)成立,则Ω2={u|u∈KerL,Nu∈ImL}在X上是有界的。 证明:令u∈Ω2,则u(t)=ctγ-n,c∈R。因此,|tn-γu(t)|=|c|。又QNu=0,由条件(H3)可知,存在t0∈(0,1],使得|u(t0)|≤M。将t=t0代入u(t)=ctγ-n中,可得|c|≤M,故Ω2是有界的。 引理12若条件(H1)—(H3)和(H5)成立,则集合 Ω3={u∈KerL|λJu+(1-λ)θQNu=0,λ∈[0,1]} 在X中是有界的。其中J:KerL→ImQ,J(ctγ-n)=c,(c∈R,t∈(0,1])是线性同构映射, 证明:任取u∈Ω3,则u=ctγ-n,λJ(ctγ-n)+(1-λ)θQN(ctγ-n)=0。 如果λ=1,则c=0;如果λ=0,由条件(H5),得到|c|≤B;如果λ∈(0,1),假设|c|>B,由条件(H5)可得到λc2=-(1-λ)θcQNu(t)<0是矛盾的。因此Ω3有界。 下面证明定理1。 a)∀(u,λ)∈[(domLKerL)∩∂Ω]×(0,1),Lu≠λNu; b)∀u∈KerL∩∂Ω,Nu∉ImL。 证明deg(JQN|KerL,Ω∩KerL,0)≠0。 令H(u,λ)=λJu+θ(1-λ)QNu,由引理12可知,H(u,λ)≠0,u∈∂Ω∩KerL。 由度的同伦不变性可得: deg(JQN|KerL,Ω∩KerL,0)=deg(θH(·,0),Ω∩KerL,0)= deg(θH(·,1),Ω∩KerL,0)= deg(θJ,Ω∩KerL,0)≠0。 由此应用引理1,可知微分方程边值问题(1)在X上至少有一个解。证毕。 考虑下述共振边值问题: (5) 并且 则条件(H4)成立。 令M=5,对任意的t∈(0,1],如果u(t)>M,那么 因此 对任意的t∈(0,1],如果u(t)< -M,那么 因此 故得到条件(H3)成立。 最后,令B=6,如果c>B,有 如果c< -B,有 所以条件(H5)成立。由定理1得到问题(5)至少有一个解。 本文运用Mawhin重合度理论,研究了共振情形下double-order Hilfer分数阶微分方程在积分边界条件下解的存在性,扩展了导数阶数的取值范围,丰富了分数阶微分方程可解性的理论,为微分方程在空气动力学、经济学、控制理论等领域的应用提供了理论参考。 本研究仅考虑了共振微分方程Lx=Nx边值问题中L是线性算子且Nx连续时的可解性,条件要求过高,未能体现出更一般化的结果。因此,在未来的研究中,将对含有p-Laplacian算子的非线性double-order Hilfer分数阶微分方程在一般化条件下解的存在性进行深入探讨,并对得到的结果进行验证。


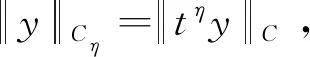


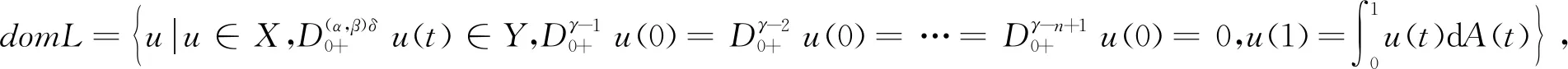
2 主要结果

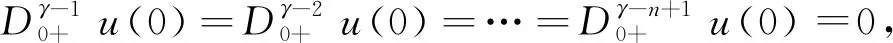







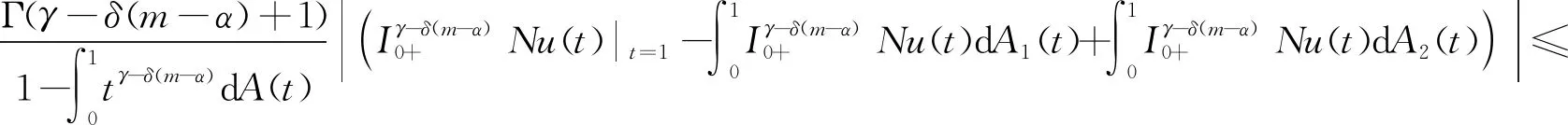


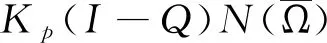

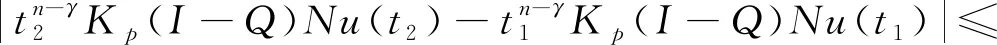
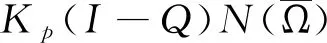

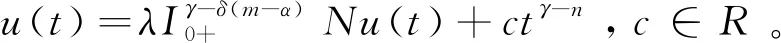

3 举 例

4 结 语
