TTE 网络通信链路自动规划方法研究*

郑小鹏，张涛，王小辉

(1.中国运载火箭技术研究院研究发展部，北京 100076；2.西北工业大学 软件学院，陕西 西安 710072)

0 引言

在航空航天、武器装备等领域，由于通信数据量呈现逐渐增大的趋势，传统的低传输总线已无法满足现有高端领域的发展需求。时间触发以太网在保留传统以太网优良特性的基础上，同时确保了实时传输业务的确定性和可靠性。

TTE 网络中的调度表用于对时间触发业务进行提前调度规划，以保证时间确定性业务的高效无误传输。然而对于消息调度中的调度表生成，目前缺少自动化部署方案的产生，仍处于比较落后的人工手动配置阶段；同时，在对实时性消息的链路规划方面也缺少相应的自动化规划方法，消息调度和链路规划过程效率底下。因此，在时间触发消息的调度中，如何设计更为可行有效的自动化部署方案来代替传统手工配置，是TTE 网络当下的研究热点之一。

在国外，Long等[1]提出了一种动态路径规划方案，该方案可以动态实时调整消息传输过程中的路由转发路径。文献[2]提出的多路径传输方案可以给每条消息计算近似最优的传输路径；全局负载均衡(Global Load Balancing，GLB)[3]算法可以选择每条消息传输的最优路径，它的性能优于动态负载均衡(Dynamic Load Balancing，DLB)[4]算法。同时，文献[5]提出的算法也可以为新消息分配最优传输路径，该算法结合了传统多路径传输方案和速率适配机制。文献[6]围绕多跳时间触发以太网的调度优化机制与算法进行了深入研究，提出一种适用于时间触发以太网的可调节时隙的高效调度算法,并通过时间触发以太网网络模型进行演示和验证，提高网络带宽资源利用率。除此以外，有很多启发式算法也用于负载均衡的研究。文献[7]提出了一种改进遗传算法来解决多协议标签交换网络(Multi-Protocol Label Switch，MPLS)的负载均衡问题。文献[8]提出了一种基于负载均衡的时间触发以太网消息调度表生成方法，为改善机载网络的消息调度性能提供了一种可行方案。

由以上分析可以看出，在负载均衡领域，面对不同的需求以及应用场景的复杂化，对负载均衡的需求也越来越多，要求也越来越高。有些传统算法无法解决的问题，启发式算法也被加入用于负载均衡的应用，有非常高的应用价值，很好地解决了负载均衡问题。

本文使用头脑风暴优化算法对TTE 网络的通信链路规划算法进行了设计，对算法的理论基础和实现流程做了详细阐述，并仿真实现了基于头脑风暴优化算法的TTE 网络通信链路自动规划方法。在负载均衡研究方向，本文主要研究基于物理链路的负载均衡，即对于网络中的链路传输，保证各个链路可以达到一种均衡的状态，避免出现有些链路过载而有些链路轻载的情况。

1 TTE 网络链路规划模型

对于TTE 网络而言，链路规划实际上就是在通信任务确定的情况下对所有通信任务的路径进行规划。

1.1 TTE 网路拓扑结构

本文采用环形网络拓扑架构。交换机之间互相连接形成环状结构，该结构不仅可以承载不同业务信息，且具有很好的容错性，如图1 所示。

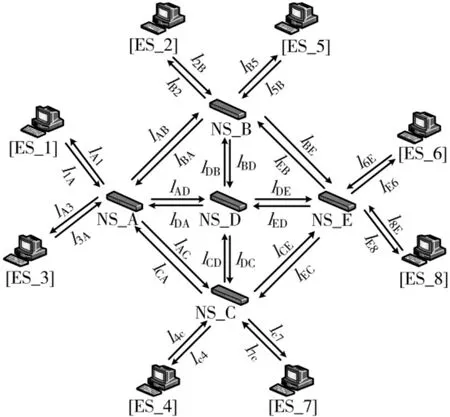
图1 TTE 网络架构拓扑

本文将以图1 的网络拓扑为例，进行链路规划算法的设计，运用图论知识，将图1 建模为无向图Graph=(V，E)。图1 中TTE 网络拓扑结构中包含了3 种物理设备类型，分别是ES、NS 和Link，用NP 表示网络中所有的ES和NS集合，NP=(ES，NS)={p1，p2，…，pnp}，np为节点数量。物理链路Link的集合定义为L，例如节点pi到pj之间的链路l(l∈L)可以表示为lij，i≠j。图2 为抽象后所形成的拓扑结构。

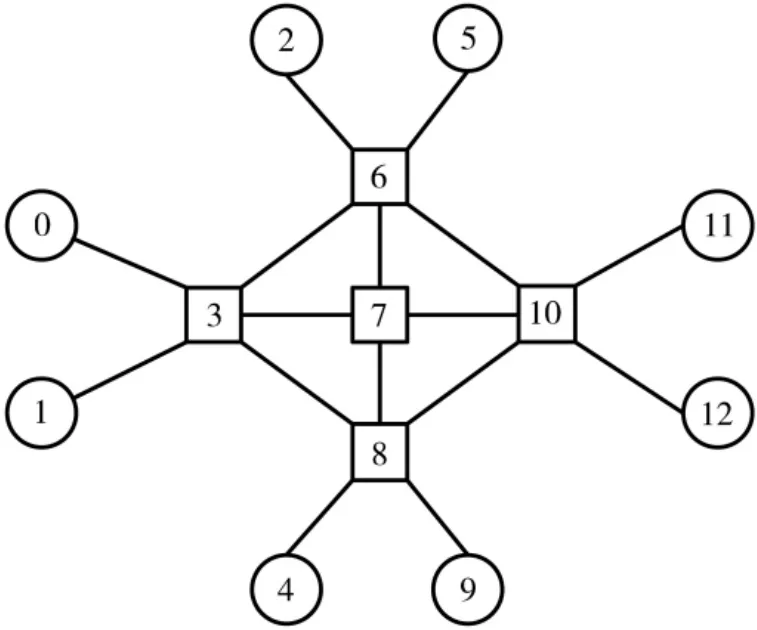
图2 抽象后的网络拓扑

采用邻接矩阵C=(cij)np×np定义节点之间的连通关系，cij表示为：

其中，cij=1 表示pi到pj之间有连接，cij=0 则表示pi到pj之间无连接。

定义通信流传输路径为Pathij：

式(2)用一个有序的链路序列代表通信流传输路径，i 表示通信流起始端点，j 表示通信流的接收端点。定义虚拟链路(Virtual Link，VL)为拓扑中所有通信流路径的并集，公式如式(3)所示：

1.2 约束条件

在给定网路拓扑和通信任务情况下，为了衡量整个网络的负载情况，避免网络拥塞，参考文献[9]做出如下定义：

式中，n 是网络拓扑中的链路数量总和，Load 计算的是网路上所有链路的负载总和。

式中，参数φ 为拓扑中所有链路的消息负载平均值，计算方式为拓扑总负载除以总的链路数量。Dk表示第k 条链路上所有消息负载的均方差。

式(8)计算了网络上的所有链路的方差，即是整个网络拓扑的方差。在目标函数的选择中，将以式(8)中的均方差来表征网络中负载均衡程度。

在每一次算法执行之后，对每一个规划好的链路都乘以当前拓扑中的消息总跳数，用以衡量当前规划结果的最短路径约束：

式中，解集x=(x1，x1，…，xn)，表示规划好的每一条链路，其中xi表示第i 条链路上规划的消息。

1.3 目标函数

在算法执行时需要使用适应度函数来描述当前规划结果的优劣，适应度高的个体更有可能会被保留下来，继续后续的迭代。适应度函数的描述方式需要提前根据应用场景进行计算，本节将推导出本文使用的目标函数，用于适应度函数的计算。

本文约束下负载均衡的描述方程表示为D(x)，最短路径的描述方程为R(x)。此时，目标函数的约束方程为：

F(x)=D(x)·R(x)(10)

由于网络拓扑中每条链路的带宽必须符合相应的最大限度带宽要求，因此，惩罚函数是在进行链路规划时的链路带宽约束条件，可以将链路最大带宽限制的最优化问题转化为带有惩罚函数的无约束限制问题，以便于问题的求解，同时惩罚函数可以对非可行解进行相应处理。具体计算公式如下：

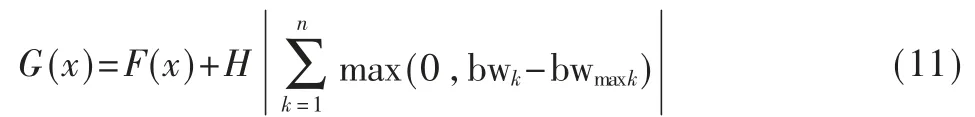
式中，bwk、bwmaxk用来描述带宽，前者是第k 条链路上目前被占用的带宽，后者是链路最大带宽；参数H 是一个无限大的正整数。当满足拓扑中链路带宽的约束限制条件时，则有bwk-bwmaxk≤0 恒成立，此时的目标函数为G(x)=F(x)+H×0，此即为可行解的目标函数值。

2 基于头脑风暴优化算法的TTE 链路规划

2.1 种群初始化

假设TTE 链路中通信流集合为Q，其中一个通信流的所有可行路径集合为Qi，它的最大路径编号为Nqi。例如在图2 所示的网络拓扑中选出3 条通信流，定义为Message1、Message2、Messag3，它们的起始节点分别是0、1、2，终止节点分别是5、4、9，可行路径及相关信息如表1 所示。此时，Q 即为3 条通信流所有的可行路径集合，Qi是Messagei 的所有可行路径集合，Nqi是Messagei的所有可行路径数目。

表1 编码示例

表1 中分别示例了每条消息的两条可行路径以及各个路径的权重因子。可行路径是通过深度优先搜索得到的可行路由，每一条通信流含有多条路径可以选择，数字1、2…代表了当前路径的编号。因此对于每一条消息，可以将每一个路径编码为自然数1、2、3…，那么经过编码后的个体可以是111、121、222 等。

2.2 划分聚类

在初始种群产生之后，需要进行划分聚类，将产生的N 个个体划分为k 个类。聚类操作可以在一组数据中发现不同数据之间的联系，将一组信息进行分类，类内的相似性越大，个体越相似，类间差别也越大，代表聚类效果越好。

在聚类时，按照种群中个体之间欧式距离的大小，将个体划分为k 个类，此时具有更加相似特征的个体会被分为同一个类。假设种群为：

其中，xi是d 维数据，将种群分为k类，即C={c1，c2，…，ct，…，ck}类，第t 个类的聚类中心为ctj。在本文进行聚类划分时，使用负载均衡和最短路径两个数据进行衡量。即种群中个体xi对应的适应值G(xi)是二维数据，第一维表示负载均衡的大小，第二维表示最短路径的大小，其表示为：

种群X 中的个体xi与聚类中心ctj的距离用dist(xi，ctj)表示。聚类中心的衡量标准用以下函数表示：

式中，E 是所有类内距离之和；dist(xi，ctj)计算的是当前个体与聚类中心之间的距离，在本文中距离的计算方式采用欧式距离，公式如式(15)所示。E 越小聚类效果越好。

聚类操作可以改善搜索区域，算法一般采用K-means、fuzzy-C-means 等。头脑风暴算法中采用的是K-means算法，聚类函数通常选用均方差的形式，公式如下：

其中，xi表示种群中的个体，vi是类ct中个体的均值，E是种群中个体均方差的和。

由于目标函数值为G(x)，当它的值越大时，得到的个体越差。但是为了易于理解，一般适应度越大，该个体的表现越好，因此，可以对目标函数值G(x)进行取倒数操作，取倒数之后的目标函数值即是适应度函数。

即适应度函数定义为：

其中，xi表示第i 个个体对应的解空间，adapt(xi)是该个体对应的适应值。此时，适应度值越高则表示想法越好，越容易被延续至下一代。

2.3 更新想法

随机思考主要用于跳出局部最优解，是聚类中心独有的操作。随机思考的过程为，首先产生一个在0～1 之间的随机数，根据这个随机数和概率Pc的大小判断是否进行随机思考，若Pc大于随机数，则随机选择一个类，将该类的聚类中心进行替换，替换的个体可以是解空间的任何一个解。

随机思考完成之后，算法会以一定的概率选择独立思考还是融合思考。假设该概率为Pot，首先产生一个随机数，若Pot大于随机数，则进行独立思考，否则融合他人。

独立思考是一个类内变异操作。在独立思考时，算法首先会根据概率Po选择需要对哪一个类进行变异。概率Po的计算公式如下：

式中，j 代表当前选择的类，numj代表第j 个类中个体的个数，N 代表种群中个体的数量。Po(j)则表示每个类中的想法占总想法的比重。

在选择好进行独立思考的类之后，需要选择使用类中哪个个体进行独立思考。此时，概率Pco决定了是否选择聚类中心作为独立思考的个体。将Pco的值与随机数进行比较，若大于随机数则选择聚类中心，否则选择除聚类中心外的其他任何一个个体。需要独立思考的个体选择完成之后，执行产生新个体的操作。在产生新个体时，根据如下公式进行选择：

其中，maxiter是最大迭代次数，curiter是当前迭代次数；kslope 表示对数函数的斜率，一般取值为20；rand()是一个0～1 之间的随机数。logsin()是一个对数传递函数，它的表达式如下：

除独立思考以外，当概率Pot大于随机值的时候，使用融合他人的方式产生新个体。融合他人的方式表示选择两个个体生成新个体，在选择个体时，可以选择两个聚类中心进行融合，也可以选择随机两个个体进行融合，具体选择那种个体取决于概率Pct和随机值的大小，若Pct大于0～1 之间的随机值则选择随机两个聚类中心进行融合，否则选择类中随机两个个体进行融合。融合规则如下：

其中，xcombined是融合后的想法；xA和xB表示两个类中的想法；λ 是0～1 之间的随机数，是混合的权重系数。假设当前选中要融合的两个个体为N1和N2，N1的第一条通信流的权重系数为(0，10，7)，个体N2的第一条通信流的权重系数为(4，9，2)，将两个个体的第一条通信流的权重因子根据式(22)进行融合，此时会产生一组新的权重系 数(0·λ+4·(1-λ)，10·λ+9·(1-λ)，7·λ+2·(1-λ))，选出该组权重系数中的最大值作为新的个体的第一条通信流权重，选择它相应的编码作为新个体的编码。对于每一条通信流都进行这样的操作之后，融合后的新个体就产生了。

2.4 算法终止条件

在独立思考和融合思考中，保留的是适应度较高的个体。例如独立思考中产生的新个体xnew的适应度高于原来的个体xold，则使用新个体替换原来的个体；否则种群不发生变化，还是保留原来的个体xold。若融合方式产生的新个体xcombined的适应度高于个体xA，则对个体xA进行替换；否则再比较个体xB。

每一轮迭代结束之后，判断是否达到预先设置的最大迭代次数。若是，算法结束，此时适应度最高的个体即是算法最优解；否则继续下一次迭代，下一轮迭代仍然从随机思考开始。同时，算法迭代次数需要选择一个合适的值，若迭代次数过少，可能解还未成熟就已经结束，只能得到次优解，影响算法的解的质量；若迭代次数过多，则会造成算法执行时间过长，影响算法整体效能。

3 仿真结果及对比分析

3.1 实验环境

拓扑环境如图3所示，图中包含13个节点，其中0、1、2、4、5、9、11、12表示为端系统，3、6、7、8、10表示为交换机。为了便于链路负载的计算，同时将链路也进行标号，表示为1～16的数字。每一条链路都是双向通信。同时，本文预先设定了500条通信流，部分通信流信息如表2所示。TT消息的一般帧长范围是(Lmin=64 B，Lmax=1 518 B)，在本文实验中，每个消息帧长设为不同的值，周期均为T=4 ms，暂不考虑其他约束条件，例如由拥塞引起的时延等。同时，每一条消息均是单源单目，即每条消息只含有一个起始节点和一个目的节点。

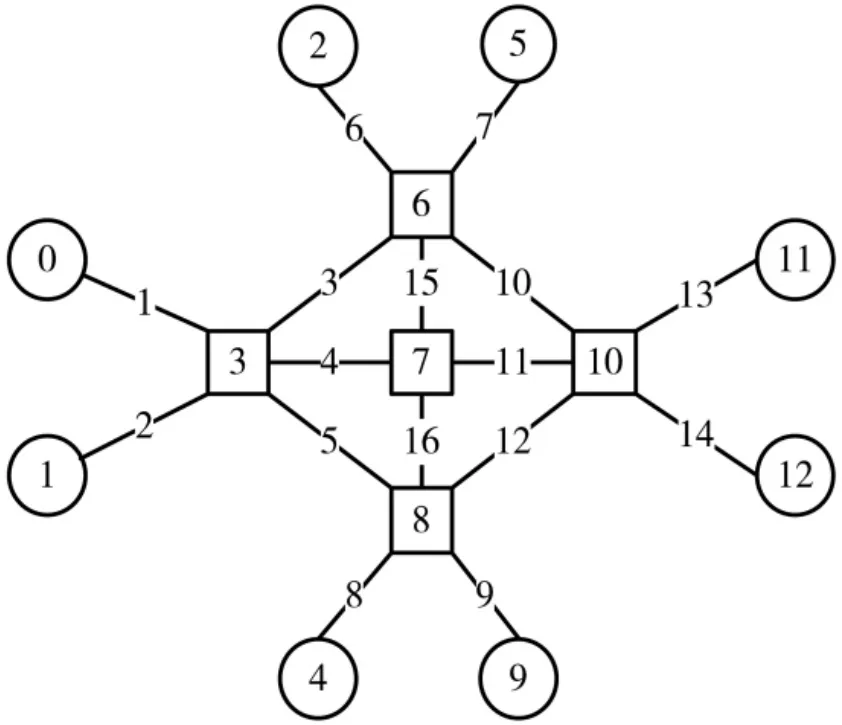
图3 抽象后的网络拓扑

在本文中，设置通信流个数为500，每个通信流含有的可行路由数routecount 是一个不定值，每条通信流都有不同的可行路由数目。将通信流Messagei 简写为Mi，表2 列出了10 条通信流的源节点和目的节点。

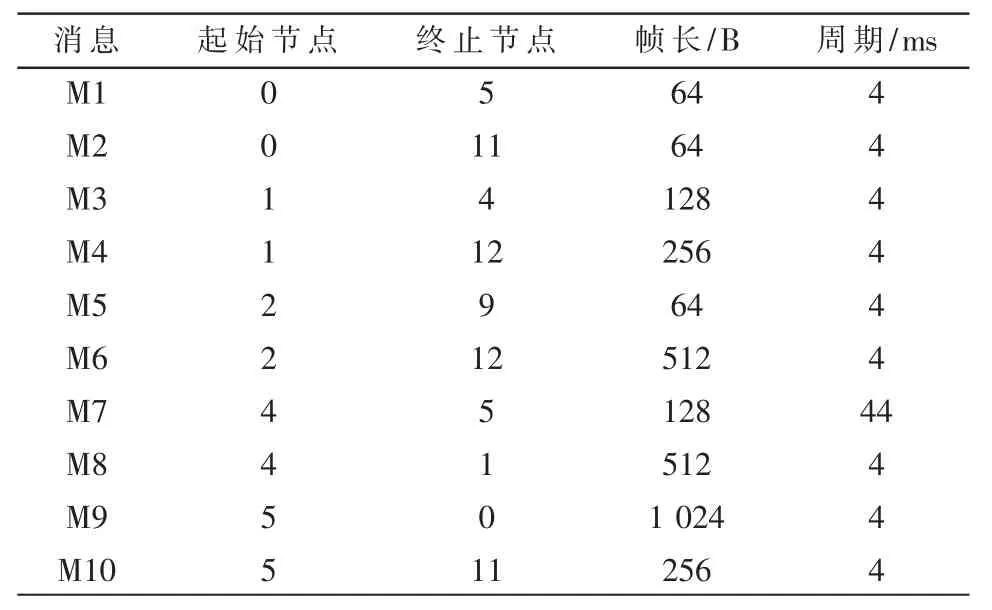
表2 TTE 网络拓扑的通信流

由此，通过深度优先搜索便可以得到500 条通信流的所有可行路径，作为算法的可行解集合。

在算法环境的配置中，种群大小设为popsize，聚类个数k=5。即一个种群中含有popsize 个个体，每一个个体都含有500 条通信流的某一个可行路径，随机数由1+rand()%routecount 确定，其中，rand()函数是用来取随机值的函数，该式可以产生1～routecount 随机数。并且在聚类划分时将种群分为5 类进行迭代。

3.2 算法结果对比分析

本文设置不同的种群数量，观察在不同的种群数量下头脑风暴优化算法和传统遗传算法呈现的变化趋势。分别给出了两种算法初始种群和最终种群中最佳个体适应度、均方差和经过的链路跳数的变化，进行了算法内部纵向比较，验证两种算法的优化效果。同时，在一定的种群数量下，给出了两种算法规划后在拓扑核心区域消息的分配情况，表征算法最优解在拓扑中的分布情况。最后根据算法迭代中适应度变化曲线对两种算法的收敛趋势进行对比分析。

头脑风暴优化算法和传统遗传算法在算法执行前后种群中最佳个体的适应度、均方差和经过链路数量的变化百分比如表3 所示。

表3 算法得迭代前后个体指标变化表

图4 和图5 是在抽象拓扑中展示了当种群数量为200时，头脑风暴算法和遗传算法链路的负载情况。其中0、1、2、4、5、9、11、12 表示端系统，端系统没有负载均衡的意义，因为对于每一条通信流，从端系统出发到达下一个节点之间的链路是唯一的，由通信流起始和终止节点决定，因此从端系统出发的线段都标记为浅灰色，不做区分。虚线框区域是由交换机组成的主干网络，所有通信流都必须经由这里到达其他节点，这里是负载均衡的核心区域。图中灰色线段的深浅表示了这条链路的负载情况。

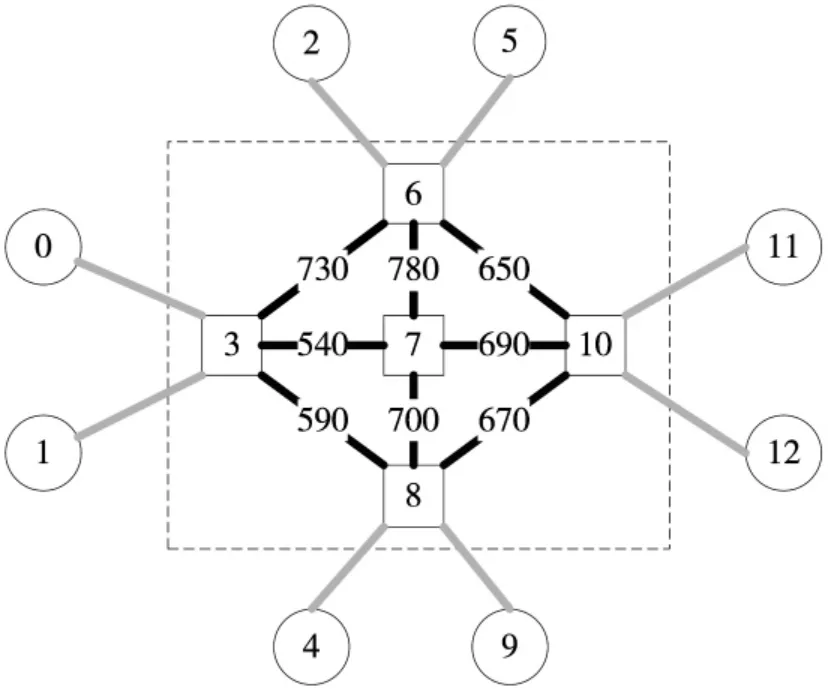
图4 遗传算法最优个体负载分布

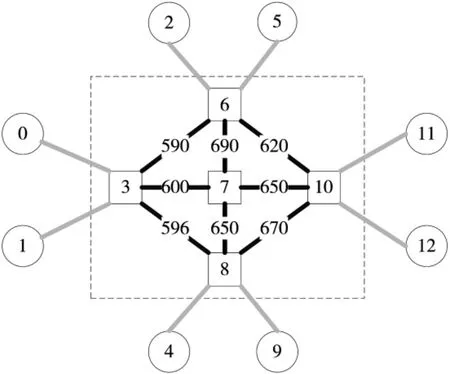
图5 头脑风暴算法最优个体负载分布

可以看出，头脑风暴算法在经过迭代后，此区域的负载已经趋近于均衡，链路上所经过的负载大部分都分布在590～690 之间。而遗传算法，负载分布在540～780之间，较头脑风暴优化算法的结果稍差。

4 结论

虽然TTE 网络目前在国外的研究已经处于非常成熟的阶段，但是目前国内还处于研究起步阶段，特别是针对TTE 网络的链路规划还鲜少有研究成果的发表。本文提出将头脑风暴优化算法应用于TTE 网络的链路调度规划，克服了手工配置的缺点，利用算法本身的自适应性，自动地对于拓扑环境下的TTE 消息进行了路径规划，提升了TTE 网络传输的效率，也增强了TTE 网络的实时性和可靠性。