有界线性算子的（R1）性质及其摄动*

赵小鹏，戴磊，曹小红

1. 渭南师范学院数学与统计学院，陕西 渭南 714099

2. 陕西师范大学数学与统计学院，陕西 西安 710119

1909 年，Weyl［1］在检查Hermitian 算子的所有紧扰动的谱集时发现，自伴算子的Weyl 谱刚好为它的谱集中非孤立的有限维的特征根，此结论后来被称为Weyl 定理。20 世纪90 年代，Weyl 定理备受关注，国内外许多学者对Weyl定理进行了变形和推广［2-4］。(R1)性质是Weyl型定理的一种变形，近期得到广泛关注［5-8］。本文主要利用拓扑一致降标性质研究了有界线性算子的(R1)性质。

1 预备知识

在本文中，用C表示复数域，N表示非负整数的全体，H表示无限维复可分Hilbert空间，B(H)表示H上的有界线性算子的全体。设T∈B(H)，如果值域R(T)为闭集且零空间N(T)的维数n(T) ＜+∞，则称T是上半Fredholm 算子；若R(T)的余维数d(T) ＜+∞，称T是下半Fredholm 算子；如果n(T) ＜+∞且d(T) ＜+∞，则称T是Fredholm算子。特别地，如果T是上半Fredholm算子且n(T) = 0，则称T是下有界算子。上半Fredholm 算子或下半Fredholm 算子统称半Fredholm 算子。当T是半Fredholm 算子时，定义ind(T) =n(T) -d(T)为T的指标。指标为零的Fredholm 算子称为Weyl 算子。算子T的升标asc(T)定义为asc(T) =inf{n∈N：N(Tn)=N(Tn+1)}，当这样的整数不存在时，记asc(T) = +∞；算子T的降标desc(T)定义为desc(T) = inf{n∈N：R(Tn)=R(Tn+1)}，当这样的整数不存在时，记desc(T) = +∞. 当asc(T)和desc(T)均有限时，可以证明asc(T) = desc(T). 称算子T是Drazin可逆的，若asc(T) = desc(T) ＜+∞. 若T是Drazin可逆且n(T) ＜+∞或d(T) ＜+∞，称T是Browder算子。可以证明T为Browder算子当且仅当T为上半（或者下半）Fredholm算子且升标和降标均有限；也可证明T为Browder算子当且仅当T为上半（或者下半）Fredholm算子且当|λ| ＞0充分小时，T-λI可逆。

设T∈B(H)，定义T的谱集σ(T)、逼近点谱σa(T)、Browder谱σb(T)、Drazin谱σD(T)分别为σ(T) ={λ∈C：T-λI不可逆}，σa(T) ={λ∈C：T-λI不为下有界算子}，σb(T) ={λ∈C：T-λI不为Browder算子}，σD(T) ={λ∈C：T-λI不为Drazin 可逆的}。记ρ(T) = Cσ(T)、ρa(T) = Cσa(T)、ρb(T) = Cσb(T)、ρD(T) = CσD(T). 令ρab(T) ={λ∈C：T-λI是 上 半Fredholm 算 子 且asc(T-λI) ＜+∞}. 用σab(T) = Cρab(T)表示算子T的Browder 本质逼近点谱。λ∈ρab(T)当且仅当T-λI为半Fredholm 算子且当0 ＜|μ-λ|充分小时，T-μI为下有界算子。

记σc(T) ={λ∈C：R(T-λI)不闭}，令ρc(T) = Cσc(T). 算子T的正规特征值的全体记为σ0(T) =σ(T)σb(T). 设E为复数集C 的子集，则分别定义isoE，accE，∂E和intE为集合E的孤立点的全体，聚点的全体，边界点的全体和内点的全体。

设T∈B(H)，称T有(R1)性质，如果

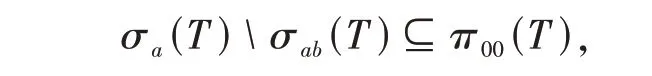
其中π00(T) ={λ∈isoσ(T)：0 ＜dimN(T-λI) ＜+∞}. 称T有(R)性质，如果

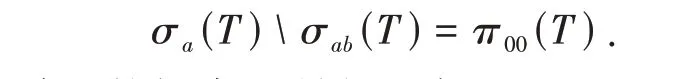
若λ0∈σ(T) ∩σD(T)，称λ0为T的极点。易知，如果T-λ0I是Drazin 可逆且n(T-λ0I) ＜+∞，则T-λ0I是Browder算子。

拓扑一致降标对算子谱的研究起到重要作用［8-9］。当T为上半（或下半）Fredholm算子时，T有拓扑一致降标性质。如果T有拓扑一致降标，则T有如下性质。

引理1［8-9］设T∈B(H)，λ∈∂σ(T). 如果T-λI有拓扑一致降标，则λ是T的一个极点。

本文首先利用拓扑一致降标性质给出了有界线性算子及其函数有(R1)性质的等价刻画；其次通过拓扑一致降标性质，给出了算子函数有(R1)性质的等价条件；之后，上三角算子矩阵的(R1)性质的稳定性得到了研究。

2 算子及其函数的(R1)性质的判定

令ρτ(T) ={λ∈C：T-λI有 拓 扑 一 致 降 标 性 质}. 记στ(T) = Cρτ(T). 易 知ρSF(T) ⊆ρτ(T)，其 中ρSF(T) ={λ∈C：T-λI为上半或者下半Fredholm算子}. 由引理1得

定理1设T∈B(H)，则T有(R1)性质的充要条件为

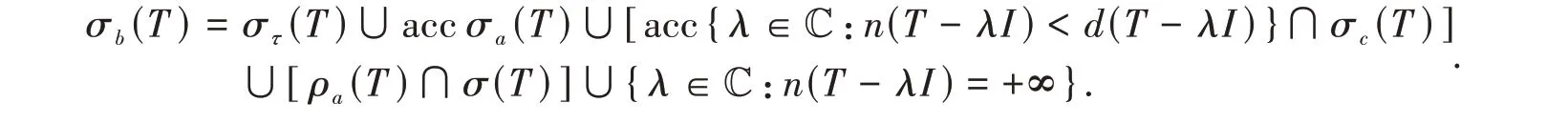
证明充分性。由于

故[σa(T)σab(T)]∩σb(T) = ∅，即[σa(T)σab(T) ⊆ρb(T)]，于是σa(T)σab(T) ⊆π00(T)，即T有(R1)性质。

必要性。不妨取λ0∈σ(T)且λ0∉στ(T) ∪accσa(T) ∪[acc{λ∈C：n(T-λI) ＜d(T-λI)}∩σc(T)]∪[ρa(T) ∩σ(T)]∪{λ∈C：n(T-λI) = +∞}. 于是λ0∈σa(T). 由λ0∉accσa(T)知存在ε＞0 使得当0 ＜|λ-λ0|＜ε时，T-λI均为下有界算子。又由λ0∉acc{λ∈C：n(T-λI) ＜d(T-λI)}∩σc(T)，分两种情况讨论：

（i）λ0∉acc{λ∈C：n(T-λI) ＜d(T-λI)}.

此时存在ε′＜ε，使得当0 ＜|λ-λ0| ＜ε′时，n(T-λI) ≥d(T-λI). 又由于T-λI为下有界算子，于是当0 ＜|λ-λ0| ＜ε′时T-λI可逆，即λ0∈isoσ(T). 由引理1 可知T-λ0I为Drazin 可逆。又由n(T-λ0I) ＜+∞，故λ0∉σb(T).

（ii）λ0∉σc(T).

结合n(T-λ0I) ＜+∞知T-λ0I是上半Fredholm 算子。又由于λ0∈isoσa(T)，于是T-λ0I的升标有限，即λ0∈σa(T) ∖σab(T). 由条件T有(R1)性质，故λ0∈π00(T)，所以λ0∉σb(T).

这 样 我 们 就 证 明 了σb(T) ⊆στ(T) ∪accσa(T) ∪[acc{λ∈C：n(T-λI) ＜d(T-λI)}∩σc(T)]∪[ρa(T) ∩σ(T)]∪{λ∈C：n(T-λI) = +∞}，反 包 含 显 然 成 立。于 是σb(T) =στ(T) ∪accσa(T) ∪[acc{λ∈C：n(T-λI) ＜d(T-λI)}∩σc(T)]∪[ρa(T) ∩σ(T)]∪{λ∈C：n(T-λI) = +∞}. 证毕

在定理1中，将[ρa(T) ∩σ(T)]改为{λ∈C：n(T-λI) = 0}，可以有下列结论：

推论1设T∈B(H)，则下列叙述等价：

（i）T有(R1)性质；

（ii）σb(T) =στ(T) ∪accσa(T) ∪[acc{λ∈C：n(T-λI) ＜d(T-λI)}∩σc(T)]∪{λ∈σ(T)：n(T-λI) = 0}∪{λ∈C：n(T-λI) = +∞}；

（iii）ρτ(T) ⊆ρb(T) ∪accσa(T) ∪[acc{λ∈C：n(T-λI) ＜d(T-λI)}∩σc(T)]∪{λ∈σ(T)：n(T-λI) = 0}∪{λ∈C：n(T-λI) = +∞}.

证明（i）⇒（ii）。由定理1 知，当T有(R1)性质时，σb(T) =στ(T) ∪accσa(T) ∪[acc{λ∈C：n(T-λI) ＜d(T-λI)}∩σc(T)]∪[ρa(T) ∩σ(T)]∪{λ∈C：n(T-λI) = +∞}. 因ρa(T) ∩σ(T) ⊆{λ∈σ(T)：n(T-λI) = 0}，所以

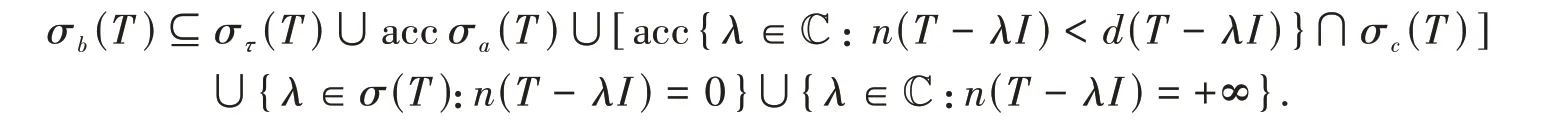
反包含显然成立。于是（ii）成立。

（ii）⇒（iii）。由（ii）知（iii）显然成立。

（iii）⇒（i）。因[σa(T) ∖σab(T)]⊆ρτ(T) 且[σa(T) ∖σab(T)]∩[accσa(T) ∪[acc{λ∈C：n(T-λI) ＜d(T-λI)}∩σc(T)]∪{λ∈σ(T)：n(T-λI) = 0}∪{λ∈C：n(T-λI) = +∞}]= ∅，故σa(T) ∖σab(T) ⊆ρb(T)，所以σa(T) ∖σab(T) ⊆π00(T)，即T有(R1)性质。 证毕

在定理1和推论1中，将accσa(T)用intσa(T)替换，结论同样成立。

推论2设T∈B(H)，则下列叙述等价：

（i）T有(R1)性质；

（ii）σb(T) =στ(T) ∪intσa(T) ∪[acc{λ∈C：n(T-λI) ＜d(T-λI)}∩σc(T)]∪[ρa(T) ∩σ(T)]∪{λ∈C：n(T-λI) = +∞}；

（iii）σb(T) =στ(T) ∪intσa(T) ∪[acc{λ∈C：n(T-λI) ＜d(T-λI)}∩σc(T)]∪{λ∈σ(T)：n(T-λI)= 0}∪{λ∈C：n(T-λI) = +∞}；

（iv）ρτ(T) ⊆ρb(T) ∪intσa(T) ∪[acc{λ∈C：n(T-λI) ＜d(T-λI)}∩σc(T)]∪{λ∈σ(T)：n(T-λI)= 0}∪{λ∈C：n(T-λI) = +∞}.

证 明（i）⇒（ii）。σb(T) ⊇στ(T) ∪intσa(T) ∪[acc{λ∈C：n(T-λI) ＜d(T-λI)}∩σc(T)]∪[ρa(T) ∩σ(T)]∪{λ∈C：n(T-λI) = +∞}显然，只需证明反包含成立。任意λ0∉στ(T) ∪intσa(T) ∪[acc{λ∈C：n(T-λI) ＜d(T-λI)}∩σc(T)]∪[ρa(T) ∩σ(T)]∪{λ∈C：n(T-λI) = +∞}. 不 妨 设λ0∈σ(T)，于是λ0∈σa(T)，因λ0∉intσa(T)且σa(T)是闭集，所以λ0∈∂σa(T). 又λ0∉acc{λ∈C：n(T-λI) ＜d(T-λI)}∩σc(T). 于是

①λ0∉acc{λ∈C：n(T-λI) ＜d(T-λI)}，存在ε0＞0，当0 ＜| |λ-λ0＜ε0时，d(T-λI) ≤n(T-λI). 而λ0∈∂σa(T). 任意0 ＜ε＜ε0，存在μ∈B°(λ0，ε)，T-μI是可逆的，因此λ0∈∂σ(T)，再根据n(T-λ0I) ＜+∞且λ0∈ρτ(T)，于是由引理1知λ0∈ρb(T).

②λ0∉σc(T)，再结合n(T-λ0I) ＜+∞，故T-λ0I是上半Fredholm 算子，因λ0∈∂σa(T)，则根据Fredholm算子摄动定理知λ0∈isoσa(T)，由定理1证明可知结论成立。

（ii）⇒（i）。若（ii）成立，由于intσa(T) ⊆accσa(T)，易证σb(T) =στ(T) ∪accσa(T) ∪[acc{λ∈C：n(T-λI) ＜d(T-λI)}∩σc(T)]∪[ρa(T) ∩σ(T)]∪{λ∈C：n(T-λI) = +∞}. 再根据定理1 可知（i）成立。

（i）⇔（iii）⇔（iv）。根据intσa(T) ⊆accσa(T)和推论1可证。 证毕

由定理1 可知，当σb(T) =στ(T) ∪accσa(T) ∪{λ∈C：n(T-λI) = +∞}时，T有(R1)性质，但是反之不成立。例如：

设T∈B(ℓ2)定义为

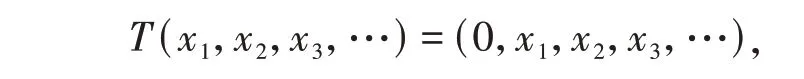
则σa(T) =σab(T) ={λ∈C：|λ| = 1}，π00(T) = ∅. 故σa(T) ∖σab(T) ⊆π00(T)，即T有(R1)性质。但是σb(T) ={λ∈C：|λ| ≤1}，στ(T) = accσa(T) ={λ∈C：|λ| = 1}，{λ∈C：n(T-λI) = +∞}= ∅，即σb(T) ≠στ(T) ∪accσa(T) ∪{λ∈C：n(T-λI) = +∞}.

推论3 设T∈B(H)，则T有(R1)性质且σ(T) =σa(T)的充要条件为σb(T) =στ(T) ∪accσa(T) ∪{λ∈C：n(T-λI) = +∞}.

证明 必要性。由定理1 知，当T有(R1)性质时，σb(T) =στ(T) ∪accσa(T) ∪[acc{λ∈C：n(T-λI) ＜d(T-λI)}∩σc(T)]∪[ρa(T) ∩σ(T)]∪{λ∈C：n(T-λI) = +∞}. 因σ(T) =σa(T)， 所 以[acc{λ∈C：n(T-λI) ＜d(T-λI)}∩σc(T)]⊆accσ(T) = accσa(T)，ρa(T) ∩σ(T) = ∅，从而σb(T) =στ(T) ∪accσa(T) ∪{λ∈C：n(T-λI) = +∞}.

充分性。只需证明σ(T) ⊆σa(T). 因ρa(T) ∩σb(T) =ρa(T) ∩[στ(T) ∪accσa(T) ∪{λ∈C：n(T-λI) = +∞}]= ∅，所以ρa(T) ⊆ρb(T)，即ρa(T) ⊆ρ(T). 证毕

下面讨论算子函数的(R1)性质。当T有(R1)性质时，并不能推出其算子函数也有(R1)性质。例如，设A，B∈B(ℓ2)定义为

令

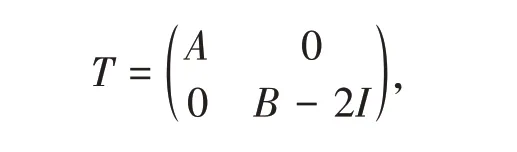
则

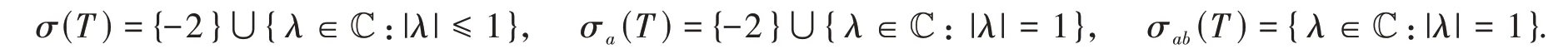
故σa(T) ∖σab(T) ={-2}⊆π00(T)，即T有(R1)性质，但对多项式p(x) =x(x+ 2)，p0(T) =T(T+ 2I)，容易看出0 ∈σa(p0(T)) ∖σab(p0(T))，但是p0(T)不是Browder算子，即p0(T)不满足(R1)性质。

定理2设T∈B(H)，则任给多项式p，p(T)有(R1)性质的充要条件是

（i）T有(R1)性质；

（ii） 若σ0(T) ≠∅，则σ(T) =σa(T).

证明必要性。结论（i）显然成立。下证结论（ii）成立。若结论（ii）不成立，因σ0(T) ≠∅，故存在λ1∈σ0(T)，λ2∈σ(T) ∖σa(T). 令p0(T) =(T-λ1I)(T-λ2I)，则0 ＜n(p0(T)) ＜+∞且0 ∈ρab(p0(T))，于 是0 ∈σa(p0(T)) ∖σab(p0(T)). 由 于p0(T) 有(R1)性 质，则p0(T) 为Browder 算 子，从 而T-λ2I是Browder 算子，于是n(T-λ2I) =d(T-λ2I) = 0，即T-λ2I为可逆算子，这与λ2∈σ(T) ∖σa(T)矛盾。因此结论（ii）成立。

充分性。设σ0(T) ≠∅. 由T有(R1)性质知σa(T) ∖σab(T) ⊆σ0(T) = ∅，从而σa(T) =σab(T). 我们知道逼近点谱和Browder 本质逼近点谱都满足谱映射定理，于是任给多项式p，都有σa(p(T)) =p(σa(T)) =p(σab(T)) =σab(p(T))，即σa(p(T)) ∖σab(p(T)) = ∅⊆π00(p(T))，故p(T) 有(R1) 性 质。此 时σ(T) =σa(T). 任给多项式p，设μ0∈σa(p(T))σab(p(T))且p(x) -μ0=a(x-λ1)n1(x-λ2)n2…(x-λk)nk，其中λi≠λj（i≠j），于是

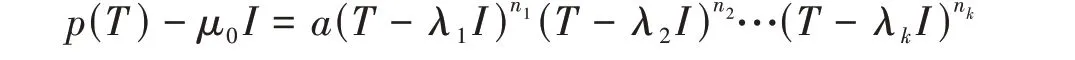
则T-λiI为上半Fredholm且asc(T-λiI) ＜+∞，1 ≤i≤k. 所以λi∈ρa(T) ∪[σa(T) ∖σab(T)]. 由于σ(T) =σa(T)，我们不妨假设λi∈σa(T) ∖σab(T)，1 ≤i≤k. 由T有(R1)性质可得λi∈σ0(T)，1 ≤i≤k. 于是p(T) -μ0I为Browder算子，即μ0∈π00(p(T)). 这样我们就证明了p(T)满足(R1)性质。 证毕

对算子T∈B(H)，σ(T) =σa(T)当且仅当σb(T) =στ(T) ∪accσa(T) ∪{λ∈C：n(T-λI) = +∞}，于是有：

推论4设T∈B(H). 则对任给多项式p，p(T)有(R1)性质的充要条件是

（i）T有(R1)性质；

（ii） 若σ0(T) ≠∅，则σb(T) =στ(T) ∪accσa(T) ∪{λ∈C：n(T-λI) = +∞}.

由推论3及推论4可知：

推论5设T∈B(H). 若σb(T) =στ(T) ∪accσa(T) ∪{λ∈C：n(T-λI) = +∞}，则对任意多项式p，p(T)有(R1)性质。

在推论5中，反之不成立。例如：设算子T∈B(ℓ2)定义为

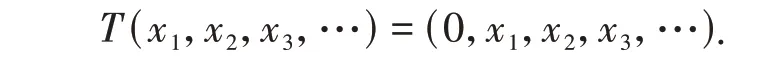
由 定 理2 可 知 任 给 多 项 式p，p(T) 有(R1) 性 质。 但 是 通 过 计 算 可 知σb(T) ≠στ(T) ∪accσa(T) ∪{λ∈C：n(T-λI) = +∞}.

推论6设T∈B(H). 若σ0(T) ≠∅，则任意多项式p，p(T) 有(R1)性质当且仅当σb(T) =στ(T)∪accσa(T) ∪{λ∈C：n(T-λI) = +∞}.

根据定理2 的证明容易看出，当σ0(T) = ∅时，对任意多项式p，p(T)有(R1)性质当且仅当T有(R1)性质。

3 上三角算子矩阵的(R1)性质的稳定性

下面设H，K为两个无限维复可分Hilbert 空间，B(K，H)为从K到H上的有界线性算子全体。再设A∈B(K)，N⊆K为A的不变子空间，则A可分解成上三角算子矩阵

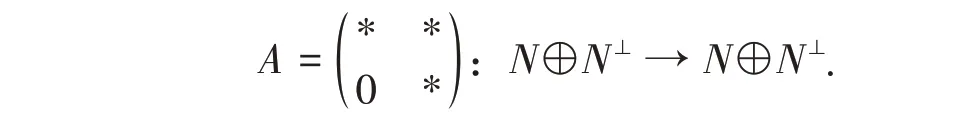
近年来许多学者研究过上三角算子矩阵的Weyl 型定理及其变化性质［10-14］。接下来我们研究上三角算子矩阵的(R1)性质。

设A∈B(H)，B∈B(K)，记

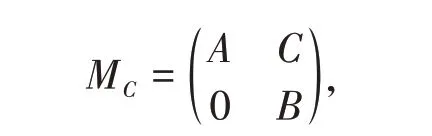
其中C∈B(K，H). 可以证明：当A和B升标有限时，对任意C∈B(K，H)，MC的升标都有限；反之，当MC升标有限时，A的升标也一定有限。

称T∈B(H)有(R1)性质的稳定性，如果任给紧算子K，T+K都有(R1)性质。

由文献［7］中定理1.1的证明可以看出下列事实：

引理2设T∈B(H). 则T有(R1)性质的稳定性当且仅当(T) = ∅. 其中(T) ={λ∈C：T-λI为半Fredholm算子且ind(T-λI) ＜0}.

设T∈B(H)有(R1)性质的稳定性，则(T) = ∅. 对任意的多项式p，由于(p(T)) ⊆p((T))，于是(p(T)) = ∅. 这样就有下列结论：

推论7设T∈B(H). 则T有(R1)性质的稳定性当且仅当对任意多项式p，p(T)有(R1)性质的稳定性。为了研究上三角算子矩阵的(R1)性质的稳定性，我们先看下列一个事实：

引理3设A∈B(H)，B∈B(K). 若A是上半Fredholm算子且d(A) = +∞，则存在C∈B(K，H)，使得

是上半Fredholm 算子且ind(MC)＜0.

证明若B是上半Fredholm 算子，则任给C∈B(K，H)，MC均为上半Fredholm 算子且ind(MC)=ind(A) + ind(B) = -∞＜0. 若R(B)不为闭集，由文献［15］中定理2.2知，存在C∈B(K，H)，使得

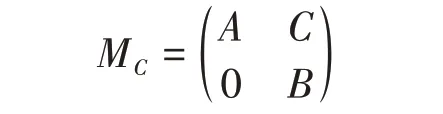
是上半Fredholm算子。由于B不为下半Fredholm算子，则由

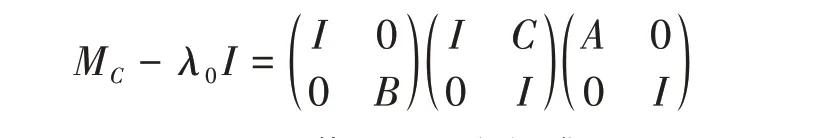
知MC不为Fredholm 算子，故ind(MC)= -∞＜0. 若R(B)为闭集，n(B) =d(B) = +∞，仍由文献［15］定理2.2知存在C∈B(K，H)，使得MC是上半Fredholm算子，且ind(MC)= -∞＜0.

下设R(B)为闭集，n(B) = +∞，d(B) ＜+∞.

由B是下半Fredholm 算子知由B不是紧算子，故其共轭算子B*不是紧算子，于是dimN(B)⊥=dimR(B*)= +∞. 设n(A) =N，取{e1，e2，…，eN+1} 为N(B)⊥=R(B*) 中N+ 1 个 正 规 正 交 集。令M=span{e1，e2，…，eN+1}. 由于dim(N(B) +M) = dimR(A)⊥=d(A) = +∞知，存在等距同构映射

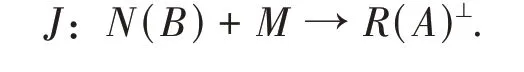
令

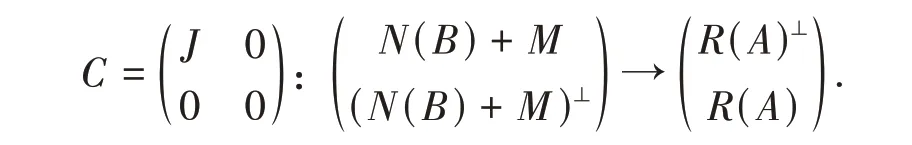
下证MC是上半Fredholm算子且ind(Mc)＜0.

（i）n(MC)=N. 设

则

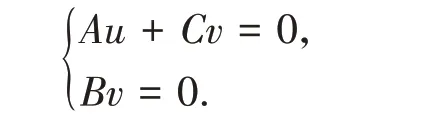
由v∈N(B)知Cv=Jv，故由Au= -Cv= -Jv∈R(A)⊥∩R(A)知Au= 0，Jv= 0. 而J可逆，故v= 0，于是N(MC) ⊆N(A)⊕{0}. 又N(A)⊕{0}⊆N(MC)，所以N(MC)=N(A)⊕{0}，从而n(MC)=N＜+∞.

（ii）R(MC)闭。设

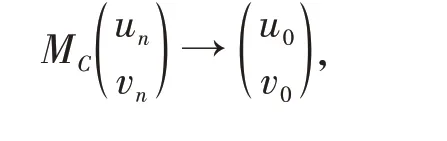
即

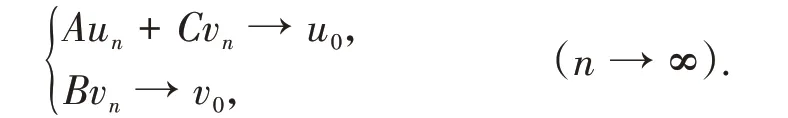
设vn=αn+βn，其中αn∈N(B) +M，βn∈[N(B) +M]⊥. 由Aun∈R(A)，Cvn∈R(A)⊥知{Aun}，{Cvn}均为Cauchy 列。而Cvn=Jαn，J可逆，故{αn}为Cauchy 列。于是由Bβn=Bvn-Bαn知{Bβn}为Cauchy 列。又βn∈[N(B) +M]⊥⊆N(B)⊥，故{βn}为Cauchy 列。从而{vn}为Cauchy 列。设vn→y0（n→∞）. 由R(A)闭知存在x0∈H使得Aun→Ax0（n→∞），故

所以R(MC)闭。

（iii）n(M*C)=N+ 1. 设

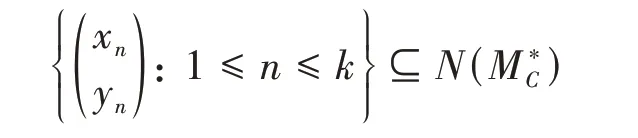
为正规正交集，则

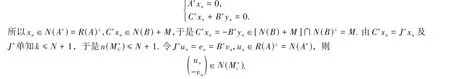
由J*可逆及{en}线性无关知

由上证明知MC是上半Fredholm算子且ind(Mc)= -1 ＜0. 证毕

证明必要性。（i）显然成立。由引理2和引理3可知（ii）成立。

充分性。由引理3，只需要证明对任意的C∈B(K，H)，(MC)= ∅即可。反证法，若不然，设λ0∈(MC)，由

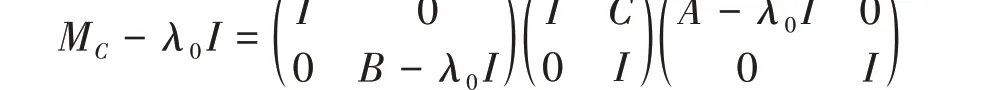
知A-λ0I为上半Fredholm 算子。由条件（ii）可知，d(A-λ0I) ＜+∞，即A-λ0I为Fredholm 算子。再次由上面的分解知B-λ0I为上半Fredholm 算子。于是M0-λ0I为上半Fredholm 算子且ind(M0-λ0I) =ind(A-λ0I) + ind(B-λ0I) = ind(MC-λ0I) ＜0，即λ0∈(M0)，这就与M0满足(R1)性质的稳定矛盾。

证毕

（ii） {λ∈C：A-λI是上半Fredholm算子，d(A-λI) = +∞}= ∅，即σSF+(A) =σe(A).

例1设A，B∈B(ℓ2)定义为

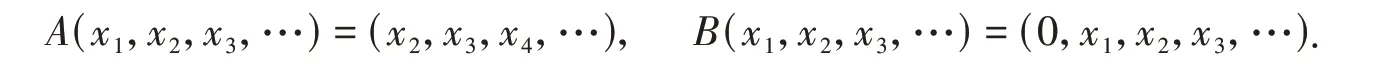
通过计算可知

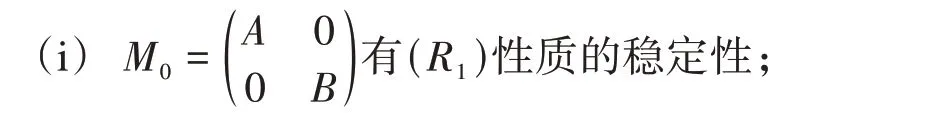
（ii） {λ∈C：A-λI是上半Fredholm算子，d(A-λI) = +∞} = ∅，即σSF+(A) =σe(A).于是由定理3，任给C∈B(ℓ2，ℓ2)，MC均满足(R1)性质的稳定性。