交错群A167上的连通7度2-传递非正规Cayley图*

李婉婷，凌波

云南民族大学数学与计算机科学学院，云南 昆明 650504

刻画有限群的结构以及利用群来刻画图的对称性，一直以来都是群与图领域的热点问题［1-4］。本文将对有限非交换单群上的非正规Cayley图进行研究。

设Γ 是一个图。其顶点集，边集，弧集以及图的全自同构群分别记作V(Γ)，E(Γ)，Arc(Γ)以及Aut(Γ)。称Γ为对称图，若Aut(Γ)在其弧集上作用传递。

设G是一个有限群，将其单位元记为1。取G中不包含单位元的集合S，称之为G的Cayley子集。设S满足S=S-1≔{s-1|s∈S}. 定义有限群G关于集合S的Cayley无向图Γ = Cay(G，S)，其中

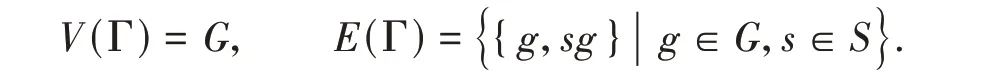
由定义可知，Γ 的度数为|S|. Γ 连通当且仅当G=＜S＞. 设R(G)为G的右正则表示，显然有R(G) ≤Aut(Γ)，且R(G)作用在V(Γ)上正则，从而可知Cayley图Γ是点传递图，我们可将群G看作是Aut(Γ)的正则子群。反之，点传递图Γ 同构于群G的Cayley 图当且仅当Aut(Γ)包含一个同构于G的正则子群（可参考文献［4］的性质16.3）。称Cayley图Γ = Cay(G，S)是正规的，若G在Aut(Γ)中正规，否则称Γ是非正规的。

正规Cayley图的概念是由徐明曜在文献［5］中首次提出。有限非交换单群上的Cayley图的正规性研究在学术界一直备受关注，而大部分这方面的研究集中在小度数的Cayley图，特别是对于图的度数≤5和度数为7 时的情形，有较多突出性的结论。例如，对于3 度图，Li［6］证明：除了7 个例外，有限非交换单群上的3度弧传递Cayley图都是正规的。在此基础上，Xu等［7-8］证明：除了A47上两个特殊情况，有限非交换单群上的3 度弧传递Cayley 图都是正规的。对于4 度图，Fang 等［9］证明：除了一系列可能的G上的Cayley图，大部分4度弧传递Cayley图都是正规的。进一步，Fang等［10］又证明：除了非交换单群M11上的两个特殊情况，有限非交换单群上的4度2-传递Cayley图都是正规的。对于5度图，Zhou等［11］证明：所有有限非交换单群上的5 度1-传递Cayley 图都是正规的。Ling 等［12］构造了交错群A39上连通5 度2-传递非正规Cayley 图的例子。对于7 度图，Fang 等［13］提出猜想：当d≤20 或者d为素数时，在有限多种情形下，有限非交换单群上的d度局部本原Cayley 图是正规的。更进一步地，Pan 等［14］证明：对于有限非交换单群G上的具有可解点稳定子群的7度弧传递Cayley图Γ，要么Γ是正规的，要么其全自同构群Aut(Γ)有一个正规子群T在弧集上传递（T是非交换单群），满足G＜T且(G，T) =(A6，A7)，(A20，A21)，(A62，A63)或者(A83，A84)，并在上述4种(G，T)情形下分别构造了一个7度G-正则的T-弧传递图。事实上，对于5度图和7度图，目前已知的有限非交换单群上的弧传递非正规Cayley 图的例子，大多是考虑了具有可解点稳定子群的情形，而对于具有非可解点稳定子群的情形，已知的结论较少。本文考虑构造有限非交换单群上的具有非可解点稳定子群的弧传递非正规Cayley图，证明了如下定理。

定理1在交错群A167上存在连通7度2-传递非正规Cayley图，且其图的全自同构群和点稳定子群分别为A168和PSL(3，2).

1 预备知识

设G是有限群，H≤G，CG(H)是H在G中的中心化子，NG(H)是H在G中的正规化子，则有下面的引理1，我们称其为‘N/C’定理，参见文献［15］的第I章定理5.7。

引理1设H≤G，则NG(H)/CG(H)同构于Aut(H)的一个子群。

设X是有限群，H为X的无核子群。对于g∈X-H满足g2∈H，定义陪集图Γ = Cos(X，H，g)为

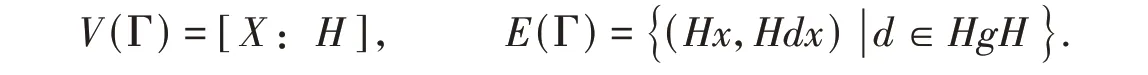
则根据陪集图的定义易证明下列引理2。

引理2设X，H和g的定义如上。令Γ = Cos(X，H，g). 则Γ是X-弧传递图且下列结论成立：

（i） val(Γ) =|H：H∩Hg|；

（ii） Γ是无向图当且仅当存在一个2-元素g∈XH使得g2∈H；

（iii） Γ是连通图当且仅当＜H，g＞=X；

（iv） 如 果X包 含 一 个 子 群G， 且G在 图Cos(X，H，g) 的 顶 点 集 上 作 用 正 则， 则Cos(X，H，g) ≅Cay(G，S)，其中S=G∩HgH.

反之，每一个X-弧传递图Σ 均同构于一个陪集图Cos(X，Xv，g)，其中g∈NX(Xvw)是一个2-元素使得g2∈Xv，v∈V(Σ)，w∈Σ(v).

下面的引理3给出了7度对称图的点稳定子群的结构，参见文献［16-17］。

引理3设Γ 是一个连通7度(X，s) -传递图，其中X≤Aut(Γ)，且s≥1. 则当s≤3且α ∈V(Γ)时，下列结论之一成立：

（i） 如果Xα可解，则|Xα|| 252，(s，Xα)见表1。

表1 可解情形的点稳定子Table 1 Vertex stabilizer of the soluable cases

（ii） 如果Xα非可解，则|Xα|| 224· 34· 52· 7，且(s，Xα，|Xα|)见表2。

表2 非可解情形的点稳定子Table 2 Vertex stabilizer of the insoluable cases

2 定理1的证明

接下来，我们构造有限非交换单群G=A167上的连通7度2-传递非正规Cayley图的例子。

构造1设G≔Alt({2，3，…，168}) ≅A167，H=＜a，b＞＜X≔Alt({1，2，…，168}) ≅A168，其中

a=(1 25)(2 26)(3 27)(4 28)(5 29)(6 30)(7 31)(8 32)(9 33)(10 34)(11 35)(12 36)(13 37)(14 38)(15 39)(16 40)(17 41)(18 42)(19 43)(20 44)(21 45)(22 46)(23 47)(24 48)(49 69)(50 70)(51 71)(52 72)(53 56)(54 55)(57 66)(58 65)(59 68)(60 67)(61 62)(63 64)(73 75)(74 76)(77 87)(78 88)(79 85)(80 86)(81 94)(82 93)(83 96)(84 95)(89 91)(90 92)(97 145)(98 146)(99 1 47)(100 148)(101 149)(102 150)(103 151)(104 152)(105 153)(106 154)(107 155)(108 156)(109 157)(110 158)(111 159)(112 160)(113 161)(114 162)(115 163)(116 164)(117 165)(118 166)(119 167)(120 168)(121 122)(123 124)(125 129)(126 130)(127 131)(128 132)(133 144)(134 143)(135 142)(136 141)(137 140)(138 139)，

b=(1 49 73)(2 50 74)(3 51 75)(4 52 76)(5 53 77)(6 54 78)(7 55 79)(8 56 80)(9 57 81)(10 58 82)(11 59 83)(12 60 84)(13 61 85)(14 62 86)(15 63 87)(16 64 88)(17 65 89)(18 66 90)(19 67 91)(20 68 92)(21 69 93)(22 70 94)(23 71 95)(24 72 96)(25 97 121)(26 98 122)(27 99 123)(28 100 124)(29 101 125)(30 102 126)(31 103 127)(32 104 128)(33 105 129)(34 106 130)(35 107 131)(36 108 132)(37 109 133)(38 110 134)(39 111 135)(40 112 136)(41 113 137)(42 114 138)(43 115 139)(44 116 140)(45 117 141)(46 118 142)(47 119 143)(48 120 144)(145 158 153)(146 157 154)(147 160 155)(148 159 156)(149 165 164)(150 166 163)(151 167 162)(152 168 161).

取x∈G为如下元素：

x=(1 61 105 53)(2 44 106 35)(3 104 107 24)(4 103 108 23)(5 122 116 75)(6 120 115 17)(7 10 114 109)(8 123 113 74)(9 19 110 118)(11 134 112 84)(12 18 111 119)(13 140 98 91)(14 139 97 92)(15 158 100 167)(16 42 99 33)(20 132 117 86)(21 63 101 55)(22 160 102 165)(25 36 45 43)(26 80 46 143)(27 68 47 52)(28 90 48 137)(29 161 32 164)(30 162 31 163)(34 62 41 54)(37 145 38 146)(39 147 40 148)(49 127 65 96)(50 151 66 155)(51 144 67 79)(56 157 64 168)(57 69 59 71)(58 70 60 72)(73 135 124 81)(76 87 121 129)(77 93 142 126)(78 94 141 125)(82 131 136 85)(83 130 133 88)(89 152 138 156)(95 150 128 154)(149 159 153 166).

定义图Γ = Cos(X，H，x).

引理4 构造1 中的图Γ = Cos(X，H，x)是连通弧传递的，它同构于G≅A167上的一个非正规Cayley图Cay(G，S)，其中S={x1，x-11，x2，x3，x4，x5，x6}，

x1=(2 163 165 56 143 147 154 34)(3 117 40 133 38 135 78 35 71 23 69 21)(4 118 64 123 98 25 158 113 44 104 101 19 106 157)(5 80 149 141 75 50 130 91 68 152 88 46 94 96)(6 111 112 45 164 166 132 110 109 52 146 155)(7 63 120 100 124 48 87 79)(8 77 36 150 74 51 93 95 131 90 151 14 85 47)(9 59 11 92 67 29 126 31 128 140 115 57)(10 97 26 30 125 32 127 13 86 60 12 58)(15 144)(16 161 167 66 137 145 156 27)(17 49 73 89 129 42 114 105)(18 107 54 160 119 61 103 102 122 99 159 139 116 41)(20 83 81 43 148 153 121 82 84 62 162 168)(22 142 76 37 136 39 134 108 53 72 24 70)(33 65)，

x2=(2 154)(3 55)(4 147)(5 115)(6 116)(7 113)(8 114)(9 140)(10 72)(11 134)(12 19)(13 99)(14 100)(15 97)(16 98)(17 59)(18 92)(20 86)(22 26)(23 61)(24 40)(25 71)(27 82)(28 81)(30 77)(31 142)(33 127)(34 75)(36 126)(39 104)(41 122)(42 96)(43 93)(45 69)(46 102)(47 136)(48 135)(49 65)(50 66)(51 67)(52 68)(53 103)(54 131)(56 133)(57 120)(58 149)(60 153)(62 85)(63 107)(64 83)(70 109)(73 121)(74 168)(76 124)(78 159)(79 158)(80 128)(84 112)(87 152)(88 151)(89 137)(90 138)(91 110)(94 162)(95 143)(106 150)(108 148)(111 118)(117 132)(119 139)(123 157)(125 163)(129 156)(130 155)(141 166)(144 167)，

x3=(2 35)(3 34)(4 59)(5 62)(6 61)(7 120)(8 168)(9 68)(12 25)(13 56)(14 39)(16 53)(17 73)(18 166)(19 45)(20 46)(23 75)(24 118)(26 143)(27 142)(28 55)(29 71)(30 72)(31 107)(32 77)(33 65)(36 133)(37 60)(38 139)(40 57)(41 164)(42 79)(43 131)(44 132)(47 162)(48 105)(49 100)(50 148)(51 121)(52 122)(54 136)(58 141)(63 89)(64 146)(66 140)(67 137)(69 98)(70 91)(76 163)(78 156)(80 90)(81 1 11)(82 112)(83 109)(84 110)(85 126)(86 145)(87 124)(92 165)(93 102)(94 101)(95 104)(96 103)(97 154)(99 106)(108 167)(114 129)(115 161)(116 125)(117 147)(123 155)(130 153)(149 157)(150 158)(151 159)(152 160)，

x4=(2 113)(3 154)(5 150)(6 108)(7 105)(9 148)(10 147)(11 78)(12 141)(13 80)(14 59)(15 120)(16 119)(19 143)(20 57)(21 163)(22 103)(24 162)(26 161)(27 106)(29 102)(30 156)(31 153)(33 100)(34 99)(35 88)(36 136)(37 86)(38 68)(39 168)(40 167)(43 134)(44 66)(45 115)(46 151)(48 114)(49 69)(50 98)(51 85)(52 112)(53 138)(54 137)(55 140)(56 139)(58 83)(61 124)(62 123)(63 122)(64 121)(65 96)(70 146)(71 79)(72 160)(73 91)(74 92)(75 89)(76 90)(77 131)(81 133)(82 117)(84 97)(87 127)(93 165)(94 144)(95 145)(101 149)(104 152)(107 155)(109 157)(110 158)(111 132)(116 164)(118 130)(125 129)(126 166)(128 159)，

x5=(5 95)(6 61)(7 35)(8 59)(9 89)(10 158)(11 48)(12 164)(13 31)(14 107)(15 75)(16 109)(21 121)(22 82)(23 141)(24 37)(25 28)(26 27)(29 93)(30 122)(32 136)(33 73)(34 157)(36 155)(38 116)(39 91)(40 110)(41 42)(43 44)(45 62)(46 84)(47 68)(49 52)(50 146)(51 137)(53 127)(54 150)(55 151)(56 71)(57 144)(58 143)(60 83)(63 159)(64 160)(65 66)(67 81)(69 132)(70 166)(72 129)(74 163)(76 156)(77 78)(79 80)(85 88)(86 87)(90 115)(92 108)(94 142)(96 135)(97 100)(98 130)(99 152)(101 167)(102 139)(103 138)(104 119)(105 161)(106 162)(111 124)(112 123)(113 114)(117 148)(118 126)(120 145)(125 128)(131 140)(133 134)(147 149)(153 154)(165 168)，

x6=(3 123)(4 111)(5 41)(6 109)(7 55)(8 56)(9 43)(10 121)(11 150)(12 149)(13 148)(14 62)(15 63)(18 66)(19 153)(22 160)(23 157)(24 72)(25 82)(26 98)(27 75)(28 126)(29 168)(30 124)(31 151)(32 114)(33 46)(34 45)(35 48)(36 47)(37 54)(38 134)(39 52)(40 112)(42 104)(44 140)(49 73)(50 74)(51 99)(53 137)(57 139)(58 97)(59 163)(60 164)(61 156)(64 88)(65 89)(67 158)(68 92)(69 93)(70 147)(71 146)(76 135)(77 113)(78 133)(81 115)(83 166)(84 165)(85 159)(91 145)(94 155)(95 154)(100 102)(101 152)(103 162)(105 142)(106 141)(107 144)(108 143)(117 130)(118 129)(119 132)(120 131)(125 161)(127 167)(128 138).

证明设Ω ={1，2，…，168}.现考虑X在Ω 上的自然作用。由Magma［18］，＜H，x＞=X，再由引理2（iii）可知，Γ是连通图。由Magma［18］，H≅PSL(3，2)且H在Ω上传递。又|H| = |Ω|，则H在Ω上作用正则。然而，G≔Alt({2，3，…，168})，显然G是点1 的点稳定子群，则X具有因子分解X=GH=HG使得G∩H= 1. 因此，Γ 同构于G≅A167上的一个Cayley 图。通过计算还可以验证|H|/|H∩Hx| = 7，由引理2（i），Γ 是7 度图。因为X是非交换单群，所以G在X中不正规，从而G在Aut(Γ)中不正规。因此，Γ 是G上的非正规Cayley图。令x1，x2，x3，x4，x5，x6和S为该引理所述，则通过计算还可得G∩HxH=S.由引理2（iv），Γ ≅Cay(G，S).

证毕

下面的引理5决定了构造1中的图的全自同构群，进而完成定理1的证明。

引理5对于构造1中的图Γ，其图的全自同构群和点稳定子群分别同构于A168和PSL(3，2).

证明令A= Aut(Γ)，V=V(Γ)，G和X的定义如构造1 中所述。首先我们假设A在顶点集V上作用拟本原。设1 ≠N是A的一个极小正规子群，则N在V上作用传递，因此N是不可解的，从而N=Td，其中d≥1，T为非交换单群。设p是|A167|的最大素因子，则有p＞7，p2不整除|A167|. 因为N在V上传递且|V| =|A167|，则p||N|. 假设d≥2，则pd||N|，由引理3，|Av|| 224· 34· 52· 7，则|A||( 224· 34· 52· 7 )·|A167|，又pd||N|||A|，pd不整除|A167|，矛盾。因此d= 1，N=T⊲A. 设C=CA(T)，则C⊲NA(T) =A，CT=C×T。如果C≠1，则由A在顶点集V上作用拟本原，可知C在V上作用传递，从而有p||C|，p2||CT|||A|，矛盾。因此，C= 1，由N/C定理，A≤Aut(T)，又T≤A，则A为几乎单群。

因 为T∩X⊲X≅A168，X是 非 交 换 单 群，则T∩X= 1 或 者X. 如 果T∩X= 1，则 由|Av|/|Xv| =|A|/|X||221· 33· 52，有|T||221· 33· 52，但p＞7，p| |N| = |T|，显然矛盾。因此T∩X=X，X≤T. 从而有|A168|||T||( )221· 33· 52· |A168|，由文献［19］的第135-136页知，T=X≅A168，A≤Aut(T) ≅S168. 如果A≅S168，则|Av| = |A|/|G| = 336，这矛盾于引理3中对点稳定子群结构的描述。因此A≅A168.

假设A在顶点集V上作用非拟本原，则存在1 ≠M是A的一个在V上非传递的极小正规子群。显然M∩X⊲X. 因为X为非交换单群，所以M∩X= 1或者X. 如果M∩X=X，X≤M，则M在V上作用传递，矛盾。因此M∩X= 1，|M|| |A|/|X|| 221· 33· 52. 设L=MX，则L=M：X.

当M不可解时，因为|M||221· 33· 52，且由文献［20］可知A5，A6和PSp(4，3)是仅有的{2，3，5}-单群，则通过比较阶的大小，容易得出M≅A5，或者A6，从而 有|M| · |A168| = |M| · |X| = |L| = |V(Γ)| · |Lv| =|A167| · |Lv|，|Lv| = 25· 32· 5 · 7，27· 33· 52· 7或者26· 33· 5 · 7，由引理3可知矛盾。

当M可解时，因为M是特征单群，所以M≅，或者，其中1 ≤r≤21，1 ≤s≤3，1 ≤l≤2. 由N/C定理，L/CL(M) ≤Aut(M) ≅GL(r，2)，GL(s，3)或者GL(l，5). 注意到M≤CL(M)，如果M=CL(M)，则L/CL(M) =L/M≅X≅A168≤GL(r，2)，GL(s，3)或者GL(l，5)，然而GL(r，2)，GL(s，3)，GL(l，5)中不包含同构于A168的子群，矛盾。因此M＜CL(M)，1 ≠CL(M)/M⊲L/M≅A168，又A168是非交换单群，则A168≅CL(M)/M. 因为| |CL(M) = |M| · |X| = |L|，CL(M) ⊲NL(M) =L，则CL(M) =L=MX，X≤CL(M)，X中心化M，所以L=M×X. 因而，Lv/Xv=L/X≅M，Lv≅Xv.M. 由引理3，当M≅时，|Lv| = |Xv| · |M| =26· 3 · 7，Lv≅ASL(3，2)，则ASL(3，2) ≅PSL(3，2).，但ASL(3，2)中没有正规子群同构于PSL(3，2)。当M≅时，|Lv| = |Xv| · |M| = 27· 3 · 7，Lv≅ASL(3，2) ×Z2，则 ASL(3，2) ×Z2≅PSL(3，2).， 但ASL(3，2)×Z2中没有正规子群同构于PSL(3，2)，矛盾。

证毕