锁相环失步对同步发电机暂态功角稳定性的影响机理分析

黎 晓，李剑泽，苏晨博，王洁聪，刘崇茹，郑 乐

（1. 新能源电力系统国家重点实验室（华北电力大学），北京市 102206；2. 中国电力科学研究院有限公司，北京市 100192）

0 引言

为实现中国“双碳”目标，据估计到2060 年新能源将逐渐成为电力供应主体，但传统的同步电源依然占有一定比例，电网仍通过交流同步机制实现功率传输［1］。新型电力系统中，多种设备的多时间尺度特性给同步发电机暂态功角稳定性问题带来新的挑战。 目前，电压源型变流器（voltage source converter，VSC）是一种常见的新能源并网设备，其中已被广泛使用的跟网型变流器（grid-following converter）依靠锁相环（phase-locked loop，PLL）与电网保持同步［2］。因此，研究变流器的锁相环和传统同步发电机互联的暂态稳定性具有重要意义。

在小扰动方面，已有较多文献研究了锁相环与同步发电机功角稳定的关系，相关的研究结论已比较成熟。例如，弱电网情况下锁相环与同步发电机转子轴承的耦合作用可能引发次同步振荡［3-4］。锁相环参数不合理时可能引起同步发电机低频振荡［5-8］，优化锁相环参数可以为同步发电机提供正阻尼［9］。

在大扰动方面，基于不同的模型和方法得到的结论并不完全一致。已有的针对锁相环与同步发电机功角的相互影响的研究认为：1）当锁相环稳定时，变流器对电网主要表现出变流器外环控制的特征，可以近似等值为恒功率或恒阻抗［10］。较多文献讨论了这种情况下新能源电源经变流器接入电网的渗透率［10-12］、接入点位置［13-15］及功率控制方式［16-17］等对同步发电机功角稳定性的影响。2）大扰动下锁相环失步时，认为锁相环动态过程的时间尺度明显小于发电机的转子时间尺度，因此，将锁相环简化为代数方程来讨论同步发电机的功角稳定性问题［18］。文献［18］指出，含变流器电网的同步发电机暂态功角失稳机理与传统电网相比，存在新的失稳约束。

然而，当变流器公共连接点（point of common coupling，PCC）处电压跌落［19-21］，或者电网强度较弱［22-23］、故障后PCC 处相位跳变［24］等情况发生时，锁相环可能失去与电网保持同步的能力［18-19］。此时，将换流器简化为恒功率源或恒阻抗无法反映出锁相环失步情况下对同步发电机的影响。当锁相环在大扰动后的暂态过程中失去平衡点时，将锁相环简化为代数方程的条件不再成立。现有的研究结论，即变流器失去平衡点后导致同步发电机失去同步的条件值得进一步研究。

本文针对上述问题，深入研究锁相环动态与同步发电机的交互影响机理，重点考虑故障后系统恢复过程中两者交互引起的同步稳定问题，而非故障直接引起的失稳情况。本文的主要贡献为：

1）建立了锁相环与同步发电机功角的动力学方程，分析了锁相环与同步发电机功角耦合的条件，揭示了大量变流器接入电网时，同步发电机功角稳定边界由不稳定平衡点约束转为锁相环约束的机理。基于几何奇异摄动理论，从理论层面解释了锁相环失去平衡点时，系统轨迹从同步发电机动态主导过渡到锁相环动态主导的动力学特征。

2）通过发电机转速的解析，分析了锁相环简化为代数方程在功角稳定性分析中的局限性，探讨了同步发电机功角稳定受锁相环制约的条件，为大规模新能源馈入电网的暂态稳定域分析提供了理论支撑。

1 锁相环与发电机功角动态交互场景描述

系统中的电力电子接口控制环节与同步发电机的转子运动具有明显的时间尺度差异。如图1 所示，内环电流控制的带宽在100 Hz 及以上，锁相环控制的带宽一般在10～70 Hz，而发电机转子的惯性时间常数通常在秒级。因此，按照不同时间尺度对系统的动态过程进行划分，能够简化分析过程。图中：为变流器的电流指令值，在文中用Id和Iq表示；θpll为锁相环的输出角；Z1、Z2、Z3为网络阻抗；ZL为PCC 处并联阻抗；为大系统母线的电压相量；Eg和δg分别为发电机内电势幅值和功角。当研究锁相环的同步稳定性时，认为同步发电机转子的相位不发生变化；当研究同步发电机的功角稳定性时，假设锁相环在合理的控制参数下能够始终保持同步，此时，变流器表现出外环功率控制或低压穿越控制的特性。

图1 变流器接入交流系统示意图Fig.1 Schematic diagram of converter connected to AC system

然而，当故障持续时间较长导致发电机的功角摆开较大时，振荡中心区域的母线电压大幅下降，进一步，可能会导致其所连接的变流器的锁相环因失去平衡点而失去同步。此时，锁相环失稳主要受发电机功角而不是锁相环控制参数的影响。同时，锁相环失去稳定之后，变流器输出的功率出现振荡，也会影响同步发电机功角的恢复过程。因此，在含电压源型变流器的电网中，同步发电机的功角稳定性可能受到锁相环的制约［18］。

锁相环对发电机功角稳定域的约束条件与传统电力系统中恒功率性质的负荷对同步发电机的功角稳定域的约束条件，具有一定的相似性，因为两者都是通过影响交流网络的功率传输能力，间接地改变了发电机的功角稳定性［25-26］。但由于存在前文所描述的时间尺度差异，两者表现出不同的现象。

简而言之，变流器平衡点存在的条件，影响了同步发电机功角稳定域的边界条件。这既是锁相环动态与发电机功角之间多时间尺度特性的表现，也是锁相环通过交流网络与同步发电机耦合的特征。

2 变流器-同步发电机系统的动力学行为

2.1 锁相环与发电机功角的双时间尺度建模

发电机的简化二阶方程如式（1）所示。

式中：ω0=（100π）rad/s 为工频50 Hz 下的角速度；TJ为标幺化的发电机惯性时间常数；Pm、Pg和D分别为发电机的机械功率、电磁功率和阻尼系数；ωg为δg的角频率标幺值，稳态下等于1 p.u.。

对于变流器和同步发电机，本文为突出机理描述，有以下假设：1）忽略电流内环控制，假设电流内环控制的带宽足够大，使得内环控制与锁相环近似解耦［27］；2）忽略外环控制和直流电压控制，假设故障及故障后恢复期间外环控制达到限幅或者故障穿越 控 制 启 动［18，20-23，28-30］，变 流 器 表 现 出 电 流 源 的 特性；3）同步发电机暂态电抗后的内电势恒定。

根据三相同步坐标系的锁相环（synchronous reference frame phase-locked loop，SRF-PLL）的 控制框图（见附录A 图A1），建立锁相环状态方程如下：

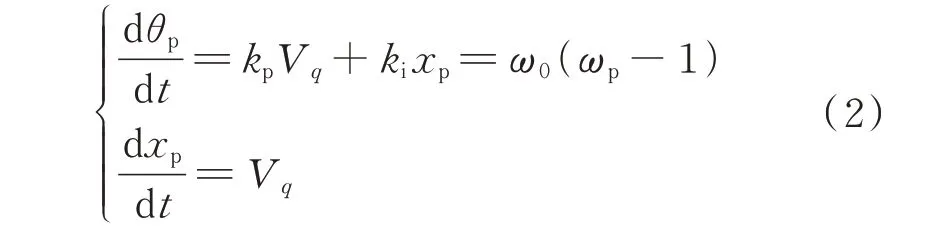
式中：θp为锁相环的直接输出角度θpll与平衡节点的相角差，是一个相对角，假设平衡节点相角的转速等于ω0，ω0和θp均 为 有 名 值；xp为 锁 相 环 比 例-积 分（PI）控制器中积分的输出值；Vq为PCC 处电压相量在q轴上的分量；ωp为角频率标幺值，稳态下等于1 p.u.；kp为 锁 相 环PI 环 节 的 比 例 系 数；ki为 锁 相 环PI 环节的积分增益。

将图1（a）中的交流电网用一个含等值大系统的三节点网络代替，本文通过如图1（b）所示的简化系统来进行机理研究。其中，等值大系统的端电压相角为0°，同步发电机和变流器分别代表发电机的一个集合和变流器的一个集合［11，31］。在风机的稳定性研究中，也常常使用单台等值风机代替整个风电场以简化研究［32］。Pg和Vq可以写成θp和δg的函数，见附录B，组合式（1）和式（2）即可得到系统的状态方程。假设锁相环的响应速度远快于发电机转子的响应速度，系统具有双时间尺度特性。通过引入无量纲参数ε=1/(kpTJ)和坐标变换，可以将系统的状态方程改写成如式（3）所示的奇异摄动的形式。

式中：yp=xpkp，为锁相环PI 控制器中积分的输出值xp与kp的乘积；λ=t/TJ为时间变量。式（3）忽略了频率变化对线路阻抗参数的影响。

基于奇异摄动理论［33］，原模型解耦为一个关于发电机转子动态的慢系统（式（4））与一个关于锁相环动态的快系统（式（5））。

针对图1（b）所示简化网络得到式（3）、式（4）和式（5）的推导过程，详见附录B。

注意到快系统（式（5））的平衡点也是慢系统（式（4））中代数方程Vq=0 的解。因此，在快系统（式（5））稳定的情况下，系统方程（式（3））的轨迹会很快趋近Vq=0 的解，如附录C 图C1 所示。此时，慢系统与快系统可以近似解耦，慢系统能够描述同步发电机的暂态功角稳定性，与传统交流电网的功角稳定性没有本质上的区别。

2.2 锁相环与发电机功角耦合条件的分析

2.2.1 快系统稳定的条件

快系统在扰动后能够恢复稳定需要两个条件：1）快系统存在稳定的平衡点；2）故障切除后轨迹位于快系统的稳定域内。

对于快系统第2 个稳定条件，已有文献分析锁相环的稳定域［34］。因为功角的变化速度显著慢于锁相环的调节速度，且功角较小时锁相环平衡点距离稳定边界有一定的稳定裕度，功角增大造成的锁相环收敛域减小难以造成锁相环失稳。也就是说，在合适的锁相环参数下，如果故障切除后锁相环能够很快恢复稳定，那么锁相环可以跟踪上发电机的功角变化。

忽略线路电导和并联电导，基于附录B 中Vq表达式（B4），Vq=0 等价于式（6）。

其中：

式中：B2和B3分别为阻抗Z2和Z3支路的电纳。已将同步发电机等值内电抗通过电路星形-三角形变换归算到网络支路中；ϕI=arctan（-Iq/Id），Id和Iq分别为变流器的d、q轴电流；I3为变流器输出电流的幅值。

由于aδ（δg）最小值在δg=π 处取得，当aδ（π）＜I3cosϕI时，发电机功角增大到π 的过程中就会使得代数方程Vq=0 失去平衡点。此时，发电机功角增大会使得快系统的第1 个稳定条件不能满足。从网络结构上表现为，B2与B3Eg越接近，锁相环越容易失去平衡点；从变流器容量上表现为，变流器输出电流越大，锁相环越容易失去平衡点。

当发电机功角增大，代数方程Vq=0 刚好失去平衡点时，将这一点记作折点F［35］，也称为鞍结型分岔点和奇异点［25］。此时，子系统（式（4））无法描述交直流电网的同步稳定性，锁相环与同步发电机的动态过程耦合，锁相环的动态过程就不能完全被忽略。本文2.3 节详细分析了这种条件下两者的交互过程。

2.2.2 慢系统的稳定边界由折点决定的条件

功角稳定边界的评估大多基于不稳定平衡点处的减速面积、暂态能量或者其稳定流形。当同步发电机功角在扰动后首先经过不稳定平衡点而不是折点时，基于不稳定平衡点的功角稳定性评估方法仍然适用。但是，当同步发电机功角增大过程中先经过折点时，折点将会影响功角稳定域的边界。

据统计，2017年我国城镇化率已达58.52%，农业转移到城镇的人口日益成为城市建设的重要参与者，也是培育农业农村发展新动能、推动农业农村现代化的重要探索者。实施乡村振兴战略，加快推进农业农村现代化，不仅能够推动广大农民在共建共享发展中实现更多获得感、幸福感和安全感，而且有利于更好践行“以人民为中心”的发展思想。[3]

本节基于发电机电磁功率Pg的解析表达式，分析了同步发电机不稳定平衡点与折点的位置关系，以及同步发电机机械功率Pm和变流器电流大小I3对这种位置关系的影响，揭示了折点影响功角稳定边界的一些运行条件。

基于附录B 的推导得到消去θp的发电机电磁功率Pg的表达式如式（9）所示。

其中：

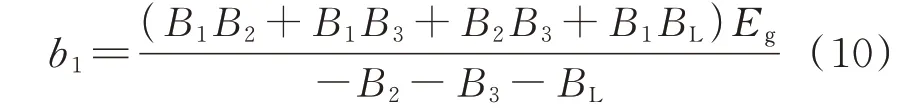
式中：b1为功率表达式中正弦分量的系数；B1为阻抗Z1支路的电纳；BL为PCC 处的并联电纳；Pg2（δg）的表达式详见附录B。在δg取值范围内，Pg2（δg）变化较小，可以简化为常数。

因此，锁相环保持在其稳定平衡点的情况下，Pg关于δg变化的曲线可以更简洁地表示为：

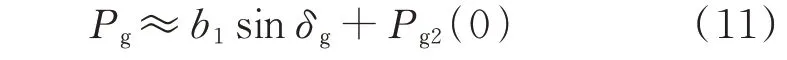
其中：

δg取值范围分以下两种情况：

情况1：当aδ（π）≥I3cosϕI时，δg的取值范围为实数域，这种情况不存在折点。

情况2：当aδ（π）＜I3cosϕI时，δg的取值范 围为[-δg，m，δg，m]，取值范围的两端为折点的位置。δg，m的表达式如下：

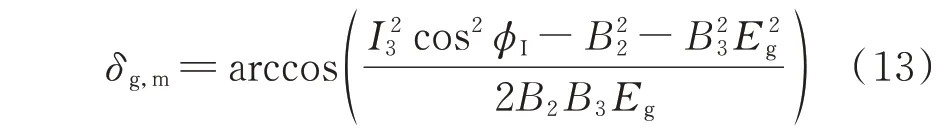
在δg取值范围的情况2 下，折点和不稳定平衡点的相对位置受变流器输出电流I3与同步发电机机械功率Pm的影响。由式（11）可知，Pg-δg曲线接近正弦函数。Pg=Pm＞0 的解中，功角较小的解称为稳定平衡点，其他解称为不稳定平衡点。由δg的取值范围可知，I3越大则δg取值范围越小。因此，I3增大可以使得在δg的取值范围之内只存在稳定平衡点，不稳定平衡点在功角δg的取值范围之外。同时，较小的Pm也会使得不稳定平衡点在δg的取值范围之外。

以附录D 表D1 的网络参数1 为例验证上述分析。同步发电机等值内阻抗为0.05 p.u.，内电势Eg=1.1 p.u.，电磁功率曲线如图2 所示。结果表明，式（11）能够很好地近似式（9），验证了利用式（11）研究Pg性质的正确性。比较图2 中不同I3条件下的Pg曲线，以及Pg=Pm的解的情况。当I3=1 p.u.或3 p.u.时，Pg=4 p.u.有两个解：稳定平衡点和不稳定平衡点。而当I3增加到5 p.u.时，Pg=4 p.u.仅有一个稳定平衡点的解，不存在不稳定平衡点，说明较大的I3使得不稳定平衡点消失。比较不同Pm条件下的解。对于Pg=2 p.u.的解，当I3=3 p.u.或5 p.u.时，δg都只有一个稳定平衡点。与Pg=4 p.u.相比，较小的Pm也会使得不稳定平衡点消失。

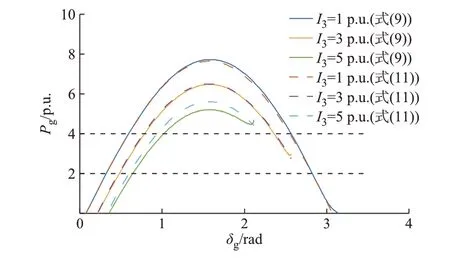
图2 同步发电机电磁功率Pg-功角δg曲线Fig.2 Curves of electromagnetic power Pg versus power angle δg of synchronous generators

因此，较大的变流器输出电流I3与较小的同步发电机机械功率Pm会使得慢系统的稳定边界由折点决定而不是不稳定平衡点。这也是后文分析的锁相环与同步发电机动态交互的一个条件，这个条件也正是大规模新能源接入电网的特点。

2.3 慢动态到快动态过程的定性分析

针对前文所描述的锁相环与发电机功角动态交互的场景，基于几何奇异摄动理论［36］，附录C 中的定理C1 对锁相环与同步发电机动态耦合的过程进行了理论解释。

由该定理可知，如果发电机功角δg在逼近折点F之前速度未减为0，那么系统轨迹将越过折点F，且在F点足够小的领域内，系统的动态过程将从式（4）所描述的慢动态过程跳跃到式（5）所描述的快动态过程。也即，系统轨迹Sa，ε沿着Vq=0 的稳定分支Sa越过折点F之后，锁相环输出角度θp几乎总是以远快于发电机功角变化的速度增大，而发电机功角δg变化较小。下一章将进一步通过分析折点F处的一些性质，得到锁相环对发电机功角稳定的影响。

3 锁相环失步对同步发电机动态的影响机理

3.1 折点附近同步发电机转速的解析分析

在折点处进行泰勒展开，以折点领域内的一点作为t=0 时刻，得到发电机转速在折点的一个很小领域内的表达式如式（14）所示。

式中：系数d1等于t=0 时刻2TJdωg/dt的值；d2等于t=0 时刻2εTJ（∂Pg/∂θp）（dθp/dt）的值；等于t=0时刻的发电机转速偏差。推导过程与d1和d2的系数表达式见附录E。

根据式（14），轨迹穿过附录C 图C2（a）所示的折点F附近区域之后进入折点F的右侧区域时，有以下两种情况：

情况1：当折点附近区域内d2＞0 时，越过折点后同步发电机转速减小。若d1＞0，发电机转速先增大后减小；若d1＜0，发电机转速单调减小。

情况2：当折点附近区域内d2＜0 时，轨迹越过折点后发电机转速增大。若d1＞0，发电机转速单调增大；若d1＜0，发电机转速先减小后增大。

基于2.3 节的分析，轨迹越过折点后锁相环输出角增加，故dθp/dt＞0。折点附近区域内dωg/dt的符号与∂Pg/∂θp的符号确定了d1和d2的负荷，决定了轨迹越过折点后发电机转速的变化趋势。

忽略线路电导和PCC 处并联负荷，得到∂Pg/∂θp的表达式（15）。由于函数的连续性，∂Pg/∂θp的符号在折点的小领域内与折点处同号，则可以用折点处∂Pg/∂θp的符号来近似表征其领域内的性质。而且基于式（15），∂Pg/∂θp=0 得到θp-δg-ϕI=2kπ，k取整数。那么在θp-δg平面上，折点右上侧的区域与折点处的∂Pg/∂θp保持同号。因此，可以用折点处的灵敏度∂Pg/∂θp估计其右侧轨迹的性质。

当折点处∂Pg/∂θp＞0时，折点领域内d2＞0，那么对应于上述情况1，轨迹越过折点后发电机转速减小，有助于发电机恢复功角稳定。当折点处∂Pg/∂θp＜0时，折点领域内d2＜0，那么对应于上述第2 种情况，轨迹越过折点后发电机转速增加，功角更容易失稳。

两种情况的示例分别如图3（b）和（d）所示，其中比较了近似解式（14）与数值解，也验证了近似解和基于近似解分析的正确性。图3（b）和（d）的转速曲线分别对应于图3（a）和（c）中折点右侧领域的绿色加粗实线轨迹。图3（a）和（c）中蓝色线表示轨迹，蓝色点表示平衡点，红色点表示折点，紫色虚线表示Vq=0 的解。本文后续图中的蓝色点和红色点表示相同的含义。

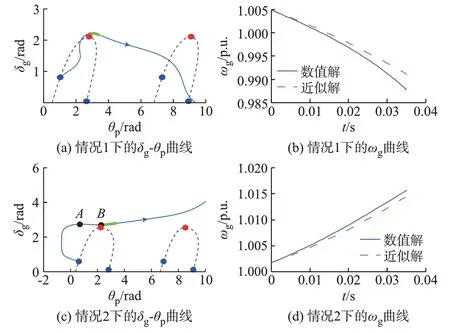
图3 越过折点F 之后的轨迹Fig.3 Trajectory after crossing fold point F

在图3（b）的示例中，d2＞0，d1＜0，根据式（14），转速为单调减小。转速减小到小于1.0 p.u.之后功角也减小，故发电机功角恢复稳定。在图3（d）的示例中，折点右侧领域d2＜0，d1＞0，根据式（14），转速为单调增加。在折点左侧领域，d2＜0，d1＜0，根据式（14），转速为先减小再增加。因此，轨迹从折点左侧到折点右侧领域时，转速经历先减小再增加的过程。折点左侧领域的转速轨迹未在图3 中画出，可以从后文更加完整的转速曲线中得到验证。

3.2 锁相环简化为代数方程的局限性

根据3.1 节对折点右侧领域内同步发电机转速的分析，变流器失去平衡点并非单一地恶化同步发电机功角稳定。简单将锁相环简化为代数方程，难以解释如图3（a）和（b）所示的情况1 的机理。

以附录D 表D1 中的网络参数1 为例，通过对数值解物理意义的分析，说明情况1 下轨迹越过折点后较长一段时间的物理过程。发电机的惯性时间常数为3.4 s，发电机等值内阻抗为0.05 p.u.，等值内电势为1.1 p.u.，D=10 p.u.，Pm=3 p.u.。锁相环参数kp=80 p.u./s，ki=1 800 p.u./s2，ε=0.003 68，I3=5 p.u.，ϕ3=0。故障切除后，系统轨迹在θp-δg平面上的投影如图3（a）中蓝色线所示。发电机的电磁功率Pg先增大再减少，如图4（a）所示，其中红色虚线表示附录C 图C2（a）中折点F左边部分Vq=0 的解Sa，斜线阴影部分表示θp增大过程中所“额外”增加的 减 速 面 积。此 时，折 点F的 坐 标（，）=（2.801 76，2.111 98），在折点处∂Pg/∂θp=1.944 44＞0，其灵敏度变化曲线如图4（b）所示。因此，轨迹越过折点F时发电机的电磁功率Pg也短时增加，形成了图4（a）中的阴影区域。其物理意义可以解释为锁相环输出角度的快速增加对发电机电磁功率的影响，改变了同步发电机功角的减速面积。

图4 动态相互作用对发电机功角稳定的影响：类型1Fig.4 Influence of dynamic interaction on power angle stability of generators:type 1

当故障更加严重时，锁相环输出角度θp增大过程中所“额外”增加的减速面积也不足以使发电机功角减速，发电机才可能失去功角稳定。在图4（a）示例的基础上，增加故障持续时间得到图4（c）所示曲线，其中θp增大过程中对应的发电机减速面积为蓝色阴影部分，对应的加速面积为红色阴影部分。虽然轨迹越过折点F之后，减速面积增大，发电机转速ωg迅速降低（对应于图4（d）中δg=2.8 rad），但ωg并未恢复到同步转速1 p.u.。随后电磁功率减小，加速面积进一步增大，发电机很快失去同步。但是，此时失稳的临界状态却没有对应的“不稳定平衡点”或者“主导不稳定平衡点”。

3.3 同步发电机功角稳定受锁相环制约的条件

3.1 节分析中的情况2 的失稳现象体现了锁相环对同步发电机功角稳定性的制约，因为锁相环动态过程恶化了发电机功角稳定，锁相环失稳与同步发电机功角失稳几乎同时发生。因此，在折点F处∂Pg/∂θp＜0 成为同步发电机功角稳定受锁相环制约的条件。

将网络参数Z2减小到1/6 p.u.，见附录D 表D1中的网络参数2。在折点处∂Pg/∂θp=-0.653 846 ＜0。系统轨迹在θp-δg平面上的投影如图3（c）中蓝色线所示，在其他平面上的投影如图5 所示。图3（c）中A点到B点之间的轨迹段对应于图5 中红色方框里的部分。

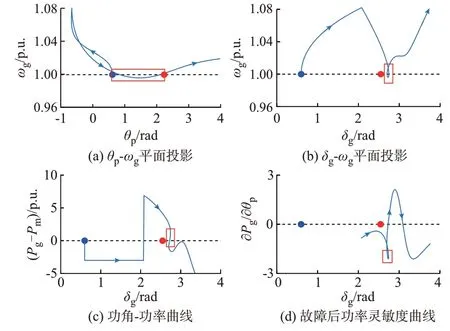
图5 动态相互作用对发电机功角稳定的影响：类型2Fig.5 Influence of dynamic interaction on power angle stability of generators:type 2

故障期间，发电机功角δg增大。故障切除后，轨迹经过A点之后功角δg开始减速并回摆，如图5（a）和（b）所示。但在轨迹经过B点之后，功角又开始加速增大，并且发电机功角失稳。在从A点到B点这一过程中，注意到两点特征：1）发电机功角轨迹在AB段之间有恢复稳定的趋势，如图5（b）和（c）所示，ωg＜1.0 p.u.满足发电机稳定判据；2）功角δg的变化很小，而锁相环输出角度θp变化范围较大。图5（c）表明，尽管功角在AB段中回摆，但功率却仍然往下跌落，与传统交流系统中发电机的功角-功率曲线不同。图5（d）说明，这个现象的原因是锁相环输出角度快速增大，且发电机的电磁功率对锁相环输出角度的灵敏度是负数，导致发电机电磁功率快速减小，功角从减速变成加速。 因此，折点处∂Pg/∂θp＜0 时，越过折点F之后，锁相环输出角度增大的动态过程成为功角失稳的一个主要原因。

4 算例分析与验证

在PSCAD/EMTDC 上搭建如附录F 图F1 所示的电路对上述分析进行仿真验证。逆变侧变流器外环采用定交流电压控制和定直流电压控制，整流侧采用有功功率控制和无功功率控制。假设故障期间直流回路的卸荷耗能电路维持直流电压的稳定。在故障期间，逆变站PCC 处电压跌落，触发低电压穿越控制模块。此时，根据电网导则要求，为了支撑交流电压，有功电流指令值等于零，无功电流指令值等于逆变站允许的最大电流-imax。锁相环PI环节的比例系数kp和积分增益ki分别为80 p.u./s 和1 800 p.u./s2，带宽约等于16.16 Hz，阻尼比ξ约等于0.94［28，37］。发电机惯性时间常数换算到100 MW 的基准值下为17 s，式（3）中的ε=0.000 74，其他参数见附录D。

4.1 算例1：锁相环简化为代数方程的局限性验证

稳态时，Pm=2.0 p.u.，I3=5.39 p.u.，ϕ3=0.38 rad，网络参数为附录D 表D1 中网络参数1。该条件属于图3 中的情况1。在0.01 s 时刻，发电机出口处母线发生三相接地短路瞬时故障。故障持续时间0.245 s 时，折点附近的轨迹见附录F 图F2 阴影部分。在这段时间内，PCC 处电压跌落严重，锁相环因此失去平衡点。角速度ωp快速增大，迅速达到了上限值1.2 p.u.，导致锁相环输出角θp快速增大，而发电机的转速逐渐减小。发电机功角δg变化较小，但发电机电磁功率快速增大，它与θp快速增大同时发生，验证了本文3.2 节的分析：∂Pg/∂θp＞0 时，θp增大初期提供的发电机P-δ平面上的“减速面积”有利于发电机保持功角稳定。

当故障持续时间增加至0.37 s 时，同步发电机才出现功角失稳，见附录F 图F3。θp快速增大导致的减速面积增加效应仍然不足以使发电机功角回摆。

4.2 算例2：同步发电机功角稳定受锁相环制约条件的验证

减小变流器与无穷大系统之间的等值线路阻抗至1/6 p.u.。稳 态 时，Pm=2.0 p.u.，I3=5.15 p.u.，ϕ3=0.3 rad。该条件属于图3 中的第2 种情况。0.01 s 时刻发生三相短路瞬时故障，故障持续时间0.385 s，锁相环和同步发电机都发生了失稳，折点附近轨迹见附录F 图F4 阴影部分。但是，系统轨迹越过折点之后表现出了与算例1 不同的特征。同步发电机电磁功率Pg在越过折点后继续下降，然后才有小幅度的回升。锁相环的快速动态没有立刻给发电机的转子运动起到减速的作用。如果故障持续时间从0.385 s 减少到0.384 s，发电机和锁相环都能保持稳定，没有算例1 中变流器失去平衡点而发电机功角恢复稳定的状态。

折点附近∂Pg/∂θp＜0，可以在接近折点F时给锁相环输出角θp施加-1 rad 的扰动来观察。0.58 s 在锁相环输出施加扰动-1 rad，持续时间0.02 s。如图6 中红色线所示，施加-1 rad 的扰动后，发电机电磁功率短时上升，说明∂Pg/∂θp＜0。而且，扰动之后发电机功角从折点位置开始回摆，θp也恢复了稳定，验证了本文3.3 节的分析：∂Pg/∂θp＜0 时，变流器失去平衡点对发电机功角稳定有恶化的作用。

图6 锁相环扰动对发电机功角稳定的影响Fig.6 Influence of PLL disturbance on generator power angle stability

5 结语

本文分析了锁相环与同步发电机交互的条件，揭示了变流器失去平衡点对同步发电机暂态功角稳定性的影响机理。本文的结论如下：

1）在故障后系统恢复阶段，发电机功角摆开过大可能使得变流器失去平衡点，导致锁相环与同步发电机的动态过程耦合。尤其在含有高比例电力电子设备和较小容量同步发电机的系统中，这种耦合更容易主导功角稳定域的边界。因此，研究高比例新能源电力系统的暂态功角稳定需要考虑锁相环的影响。

2）根据折点附近锁相环输出角度变化对发电机电磁功率的灵敏度符号，锁相环与发电机的交互作用可分为两种类型：（1）锁相环输出角的快速变化为发电机提供了额外的减速面积，在一定程度上改善了发电机的暂态功角稳定性；（2）锁相环输出角的快速变化恶化了发电机的暂态功角稳定。锁相环对同步发电机功角稳定的制约体现在第2 种类型，因此，对于功角稳定性分析需要着重考虑第2 种类型。该结论对研究含电压源型变流器和同步发电机的电力系统的功角稳定边界条件、在线稳定评估等具有参考意义。

3）本文探讨了锁相环与同步发电机之间的非线性现象。由于在解析分析时截断了三阶及以上的高阶项，然后结合数值计算现象对解析结果进行了推广，本文分析结论适用于锁相环失稳后的短暂时间。同时，如果锁相环失稳时间较长也会触发继电保护动作导致变流器闭锁。此外，本文的研究基于单个变流器聚合模型和单个发电机模型。对于更复杂的多变流器和多机系统，本文的结论是否需要修正仍需要进一步研究。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。