极限视角下的函数零点问题
2022-11-28赵景刚吴莉娜
赵景刚 吴莉娜
(江苏省常州高级中学,213003)
函数零点问题一直是高考的重点与难点,函数极值与最值、不等式恒成立等问题也会涉及到函数零点问题.对于函数零点问题,可以借助函数零点存在定理及函数单调性判断零点的存在性,而如何判断并找到异号的函数值是解决该类问题的关键.导数是研究函数性质的有力工具,其本身就是由极限定义的,从“极限”的视角认识研究函数性质是必要的并且是合理的.
一、必备知识与方法
不同的函数模型有不同的“变化趋势”,对不同函数“变化趋势”的研究和比较,可以加深对函数性质的理解. 通常可以通过常见的两个不等关系,给出指数函数、对数函数与幂函数“变化趋势”量化关系.
1.常见放缩
2.洛必达法则
二、函数极限组合类型
历年的高考试题主要考查由指数函数、对数函数、幂函数组成的超越函数导数问题,对这类函数极限组合类型进行讨论研究,可以更好地研究函数性质,帮助我们找到处理函数零点问题的一般方法.
1.“∞+有界”型
例1(2020年高考数学山东卷第21题)已知函数f(x)=aex-1-lnx+lna.(1)当a=e时,求曲线y=f(x)在点(1,f(1))处的切线与坐标轴围成的三角形的面积;(2)若f(x)≥1,求a的取值范围.
分析本题第(2)问是含参数的不等式恒成立问题,可将其转化为函数最值问题进行处理.通过对导函数零点的研究,得到函数的单调性及最值.
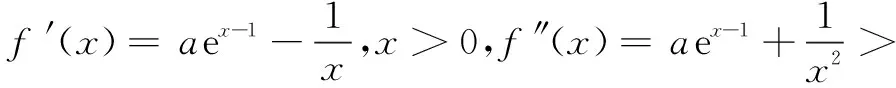
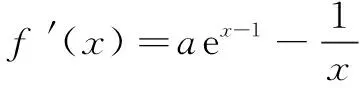
2.“∞-∞”型
例2(2021年高考数学浙江卷第22题)设a,b为实数,且a>1,函数f(x)=ax-bx+e2(x∈R).(1)求函数f(x)的单调区间;(2)若对任意b>2e2,函数f(x)有两个不同的零点,求a的取值范围.
分析本题第(2)问是含参数的函数零点问题,可以先考虑条件成立的必要性,初步确定参数a的范围,再从极限的视角判断并确定函数零点.
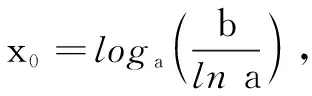
点评对于函数极限“∞-∞”型,该极限类型中有两个“∞”,需要确定起主要作用的“∞”,在“极限”视角下分析判断函数零点存在的基础上,把含有两个“∞”的“超越”不等式放缩成可解不等式.在本题中,当1
例3(2018高考数学全国2卷第21题)已知函数f(x)=ex-ax2.(1)若a=1,证明:当x≥0时,f(x)≥1;(2)若f(x)在(0,+∞)只有一个零点,求a.
分析在研究导数问题时,对什么函数进行求导是顺利解题的关键.本题第(2)问,若对原函数直接求导,会涉及二阶导函数零点问题,不易处理,依据原函数结构特征,可以构造并研究新函数(分式函数)零点问题.
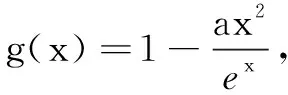
(i)当a≤0,g(x)>0,g(x)没有零点;
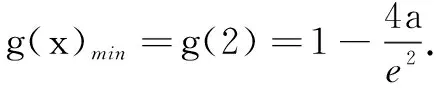
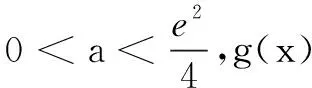

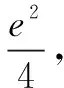
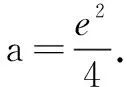
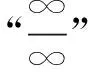
对于函数零点问题,通过类型归纳概括、得到如下解题思维导图(如图1):若函数问题涉及函数零点问题,先对函数(导函数)极限类型进行分析,再利用指数函数、对幂函数级别关系或洛必达法则判断函数零点是否存在,在函数存在零点的基础上,借助放缩法、有界控制法、观察法等进行取点,从而得到函数(导函数)单调性,最终解决函数问题.
知识方法源于课本又高于课本,在日常教学中,需要注重高考与教材相结合.一方面依据考纲,从高考题中获取知识方法,培养学生思维能力和核心素养,找到攻克同一类型题目的解题要领. 另一方面注重回归课本,从教材中寻找源头,充分挖掘教材中的数学本质和数学思想方法.
在复习备考中,需要引导学生对重点、难点题型进行归纳研究,寻找解决不同问题的一般规律和方法. 因此,高三复习更适合微专题教学,重视微专题的教学设计,“因微而准,因微而细,因微而深”,帮助学生构建丰富联系的知识系统,促进学生深度学习.
高考中借助函数零点问题综合考查函数、导数等相关知识,侧重考查分类、转化、数形结合等数学思想.而解决该类题型的关键是如何判别并确定函数的零点,通过寻找教材中的“源”——指数函数、对幂函数“变化趋势”的不等关系,借助不等式放缩,成功找到攻克函数零点问题的一般思路和方法. 总而言之,“以高考为抓手,以教材为根本”能够有效引领高三复习,帮助学生在解决数学问题过程中有的放矢.
