例析新情境试题的考查要点及复习建议
2022-11-28王菊张琥
王 菊 张 琥
(1.江苏省苏州市苏州高新区第一中学,215000;2.北京外国语大学附属苏州湾外国语学校,215000)
数学学科中的情境分为课程学习情境、探索创新情境和生活实践情境.高考命题指向是:以课程学习情境为检验基础的量尺,以探索创新情境为区分甄选的手段,以生活实践情境为拓展应用的渠道.新情境问题是每年高考试题中的亮点之一.此类问题需要从新情境中提取有效信息并作答,考查基础知识的迁移运用、分析解决实际问题的能力.本文精心选择一组情境新、信息量大和有一定思维深度的题目分类讨论其考查要点,以期对复习应考有所帮助.
一、 数学文化
高考试题中对数学文化的考查,主要涉及中国古代数学名著,数学家或数学家故事,或数学名题等.
例1(2021年全国乙卷理科)魏晋时期刘徽撰写的《海岛算经》是关于测量的数学著作,其中第一题是测量海岛的高.如图1,点E,H,G在水平线AC上,DE和FG是两个垂直于水平面且等高的测量标杆的高度,称为“表高”,EG称为“表距”,GC和EH都称为“表目距”,GC与EH的差称为“表目距的差”,则海岛的高AB=( )

评析本题以魏晋时期我国数学家刘徽的著作《海岛算经》中的测量方法为背景,让学生充分感受我国古代数学家的聪明才智.考查相似三角形的性质、比例的性质、直角三角形的边角关系和推理能力与计算能力,属于基础题.解题关键是根据相似建立比例式,围绕所求目标进行转化.

(A)C的蒙日圆的方程为x2+y2=3b2
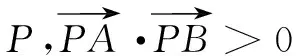

(D)若矩形MNGH的四条边均与C相切,则矩形MNGH面积的最大值为6b2

二、新定义(概念)
新定义(概念)问题是指在现有的运算法则和运算律的基础上定义一种新的概念或运算规则或性质等问题.新定义可以文字的形式出现,也可以数学符号或数学表达式的形式出现,有的甚至举例说明.在高考中,有关新定义的考题偶尔会出现,要么在小题的压轴题中出现,要么在解答题中出现,主要考查数学抽象、直观想象、数学运算和逻辑推理等核心素养.
例3(2021年北京卷)定义Rp数列{an}:对实数p,满足:①a1+p≥0,a2+p=0;② ∀n∈N*,a4n-1 (1)对于前4项2,-2,0,1的数列,可以是R2数列吗?说明理由; (2)若{an}是R0数列,求a5的值; (3)是否存在p,使得存在Rp数列{an},对∀n∈N*,Sn≥S10?若存在,求出所有这样的p;若不存在,说明理由. 解析(1)由条件③ 结合题意可知0=a3∈{a1+a2+2,a1+a2+2+1}={2,3}矛盾,故前4项2,-2,0,1的数列,不可能是R2数列. (3)令bn=an+p,由条件③可知:∀m,n∈N*,bm+n=am+n+p∈{am+p+an+p,am+p+an+p+1}={bm+bn,bm+bn+1},由于b1=a1+p≥0,b2=a2+p=0,b4n-1=a4n-1+p 评析根据新定义来解决问题,有时还需要用类比的方法去理解新的定义,这样有助于对新定义的透彻理解.透过现象看本质,考查的还是数学基础知识的运用. 信息迁移题是由题干给出信息,要求考生运用所学的数学知识解决新情境中的相关问题.此类试题材料新颖、构思别致、有一定的思维量.考查学生的自主学习能力、阅读理解能力以及迁移创新能力.解题时要能利用外显信息正确模仿迁移、排除干扰信息、挖掘隐含信息、注重联想类比. 例4(2021年全国新高考Ⅱ卷)北斗三号全球卫星导航系统是我国航天事业的重要成果.在卫星导航系统中,地球静止同步卫星的轨道位于地球赤道所在平面,轨道高度为36 000 km(轨道高度是指卫星到地球表面的距离).将地球看作是一个球心为O,半径r为6 400 km的球,其上点A的纬度是指OA与赤道平面所成角的度数.地球表面上能直接观测到一颗地球静止同步轨道卫星点的纬度最大值为α,记卫星信号覆盖地球表面的表面积为S=2πr2(1-cosα)(单位:km2),则S占地球表面积的百分比约为( ) (A)26% (B)34% (C)42% (D)50% 评析本题考查U的近似计算,充分理解题中的计算方法是解题的关键,考查推理能力与运算求解能力,属中档题. 在高考试卷中,以高等数学知识为背景的试题时有出现,涉及到的高等数学知识主要有欧拉公式、极限思想、特征函数、高斯函数、函数的凹凸性、洛必达法则、不动点定理等.这类问题主要考查数学抽象、逻辑推理和数学运算等核心素养. 例6(2016年全国卷)Sn为等差数列{an}的前n项和,且a1=1,S7=28.记bn=[lgan],其中[x]表示不超过x的最大整数,如[0.9]=0,[lg 99]=1. (1)求b1,b11,b101; (2)求数列{bn}的前1 000项和. 解析(1)设{an}的公差为d,据已知有7+21d=28,解得d=1.所以{an}的通项公式为an=n.b1=[lg 1]=0,b11=[lg 11]=1,b101=[lg 101]=2. 所以数列{bn}的前1 000项和为1×90+2×900+3×1=1 893. 例7在三维空间中,定义向量的外积:a×b叫做向量a与b的外积,它是一个向量,满足下列两个条件:①a⊥(a×b),b⊥(a×b),且a,b和a×b构成右手系(即三个向量的方向依次与右手的拇指、食指、中指的指向一致,如图2所示);②a×b的模|a×b|=|a|·|b|sin〈a,b〉(〈a,b〉表示向量a,b的夹角)在正方体ABCD-A1B1C1D1中,有以下四个结论,正确的有( ) 高考中引入新情境试题,就是要求重视数学文化知识的学习和数学阅读能力的提升.在复习中,通过高考真题来充分挖掘教材中的图片、表格、阅读材料等信息,自主提出问题,熟悉试题的考查要求,掌握试题的设计意图、设问角度、呈现形式. 情境的创设是基于生活实际,接近真实情境.需要多阅读与数学有关的报刊杂志,不断提高自己对情境材料的信息提取、图表的分析与数据处理能力,要能从问题情境中蕴涵的数学知识、数学思想等角度全面剖析,强化信息获取与解读能力,构建系统的、从低阶到高阶的问题思维链,逐步提升分析问题、解决问题的能力. 试题的情境与已有知识经验具有一定的间隙,这就需要进行知识重构,从而使知识“活起来”,同时有利于自主选择解答路径与方法,并能有效地调动智力和非智力因素.新情境试题在促进知识的建构、培育学科素养、发展数学核心素养等方面,都具有积极的引导作用.在复习中,应加强对新情境试题的学习与训练.
三、信息迁移


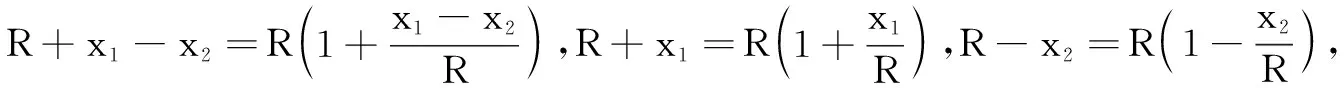
四、高等数学知识

