基于PBES-LS-SVM的锂离子电池组SOC预测
2022-11-26李晟延马鸿雁窦嘉铭
李晟延,马鸿雁,2,3,窦嘉铭,王 帅
(1.北京建筑大学 电气与信息工程学院,北京 100044;2.建筑大数据智能处理方法研究北京市重点实验室,北京 100044;3.智慧城市国家级虚拟仿真实验教学中心,北京 100044)
锂电池作为常用的环保储能设备之一,对“3060”碳达峰、碳中和目标的达成起着重要支撑作用。锂电池荷电状态是反应电池性能的标准之一。锂离子电池在使用过程中,准确预测电池组荷电状态(state of charge,SOC)能够及时预防电池过充、过放等违规操作对电池寿命造成损害。目前,SOC预测领域较为常用的方法有:卡尔曼滤波法[1]、传统估计法[2]和数据驱动法[3]。
基于卡尔曼滤波法是SOC离线预测研究中较多的方法之一。王文亮等[4]采用最小二乘法实现电池模型参数的在线估算,结合扩展卡尔曼算法对SOC进行估算,预测精度得到了提高。但该方法需要依靠精确的电池等效电路模型,预测对象大多为单体电池,对于锂离子电池组的SOC研究较少。传统估计法分为开路电压法与安时积分法,其中安时积分法[5]受温度环境与充放电流影响较大,文献[6]指出开路电压法需要电池长时间处于静止状态,通过实验得到端电压与SOC之间的关系,该方法无法进行SOC的实时估计且温度变化会对预测方式产生影响。刘春辉等[7]设计了基于SOC的DC/DC 变换器主动均衡电池管理系统,解决了动力电池组中各单体电池SOC值的不一致性问题,均衡效果较好。
数据驱动法可以略去电池内部的机理反应,将电池作为“黑箱模型”省去了参数辨识的过程,利用神经网络建立起电池相关参数和荷电状态之间的映射关系[8]。刘秋丽等[9]将粒子群算法优化BP 神经网络模型应用在动力电池组荷电状态的预测,验证了粒子群算法优化模型的快速性与稳定性。孙小川[10]通过改进粒子群算法对BP 神经网络进行优化,然后对网络模型进行剪枝处理,对燃料电池组SOC进行预测,预测效果较好。但上述模型容易陷入局部最优,导致SOC预测精度较低。为解决这一问题,学者们提出将支持向量机[11-12]在小样本和非线性预测问题上的优势应用到锂电池荷电状态的预测中。
本文采用主成分分析对锂电池组放电过程中的影响因素进行评估与筛选用于提高数据质量,利用新型元启发式算法中的秃鹰搜索算法(bald eagle search,BES)对最小二乘支持向量机(least squares support vector machine,LS-SVM)中参数寻优环节进行优化,构成PBES-LS-SVM 网络模型对锂离子电池组的SOC进行研究,以获得更加准确的电池组SOC预测模型。
1 预测模型
1.1 秃鹰搜索优化算法数学模型
秃鹰搜索优化算法是由马来西亚学者Alsatter[13]在2020年提出的集群智能算法之一,自然界中,秃鹰的体型较大,这使得它们站在食物链的顶端[14]。秃鹰的狩猎阶段分为三个阶段:选择空间、空间搜索猎物、俯冲[15]。秃鹰捕猎的三个阶段数学模型如下:
阶段1:选择空间阶段,盘旋的秃鹰,会基于鲑鱼个体或种群的浓度来选择空间。从原定位置朝选定的空间飞行。这一行为在数学上被定义为:
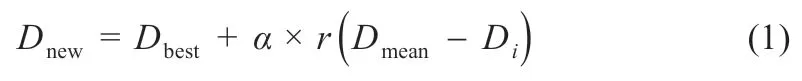
式中:α为控制位置变化的参数,取值范围在[1.5,2]之间;r为(0,1)范围内的随机数;Dbest为当前秃鹰搜索确定的最佳搜索位置;Dmean为先前搜索结束后秃鹰的平均分布位置;Di为第i只秃鹰的位置。
阶段2:空间搜索猎物阶段,秃鹰通过在选定的螺旋空间内向不同方向移动来寻找搜索猎物。此外,确定最佳猎物和俯冲的最佳位置。猎取猎物和俯冲的最佳位置被确定。这种行为在数学上被定义为:
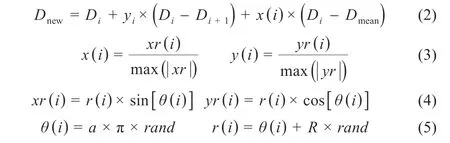
式中:Di+1为第i只秃鹰下一次更新位置;x(i)与y(i)为极坐标系下秃鹰的位置,取值范围为(-1,1);θ(i)为螺旋方程的极角;α为一个常数参数,取值范围在[0,5]内;r(i)为螺旋方程中的极径;R为另一个常数参数,取值范围为[0.5,2];rand为(0,1)之间随机参数。
阶段3:俯冲阶段,秃鹰从搜索空间中的最优位置快速俯冲飞向目标猎物,秃鹰种群中其他个体也同时向最佳位置摆动俯冲攻击猎物,定义为:
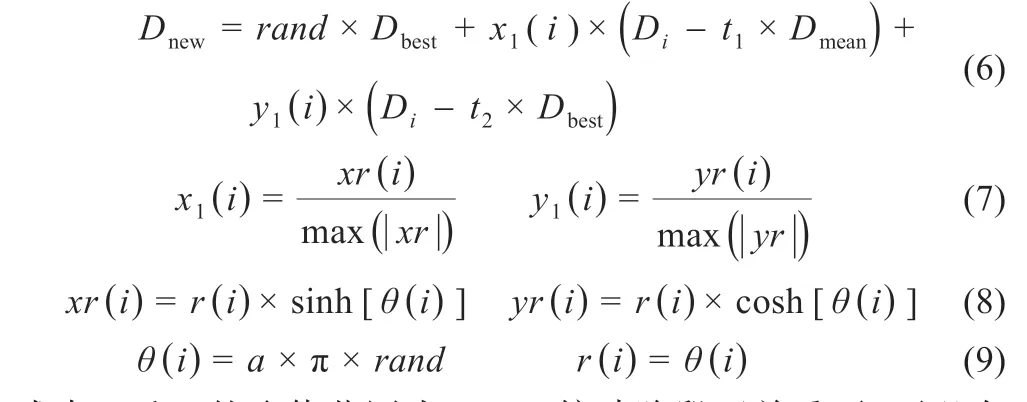
式中:t1和t2的取值范围为[1,2]。俯冲阶段至关重要,可以在设定的迭代次数中找到最优的解决方案。
1.2 最小二乘支持向量机
SVM 算法是一种以统计学理论为基础的传统机器学习方法,该方法可以在模型的复杂性与学习能力之间寻求最佳的折中,并获得最好的推广能力。而最小二乘支持向量机(LS-SVM)在传统的SVM 上利用最小二乘线性系统作为损失函数,将SVM 中优化问题的不等式约束转化为等式约束,以此对传统SVM 进行优化。而BES 算法则是用来优化LSSVM 中的参数g与C的选择,用于提高LS-SVM 中的性能与效率,更准确地对数据进行计算。
在锂电池组SOC估算问题的研究背景下,非线性映射为ψ(x),其主要目的是将其映射到一个高维空间中,以方便线性回归运算的方法将低维的非线性转换到高维空间中,并构造最优线性决策函数:
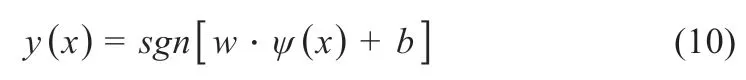
式中:w为权向量;b为常数。利用SRM 准则构造下面的最小化目标函数为[16]:
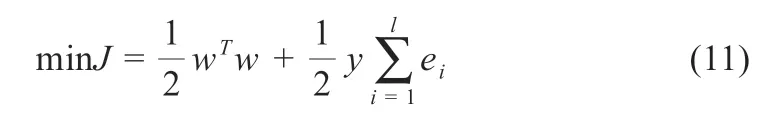
式中:y为调整参数;ei为松弛变量。通过核函数K(xi,xk)的引入可以得到LS-SVM 模型为[17]:
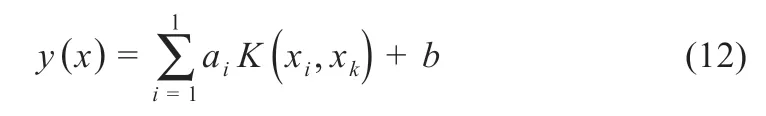
本文中,PBES-LS-SVM 网络模型训练集维度通过主成分分析法,将维度由原有的5 维降为3 维。高斯径向基函数构造的支持向量机训练参数相对较少,更容易确定参数,所以在核函数的选择上采用高斯径向基函数,即:
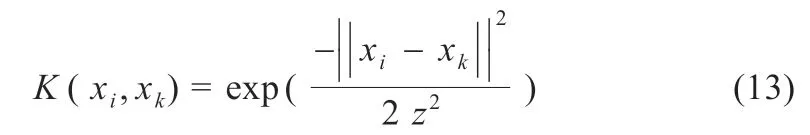
式中:z为高斯核宽度。
1.3 PBES-LS-SVM 预测模型
LS-SVM 中参数优化对于模型预测的准确性十分重要。因此本文选择PCA 对锂电池组放电过程中的影响因素进行评估与筛选用于提高数据质量,并利用元启发式算法BES 优化参数g和C。其流程如图1 所示。
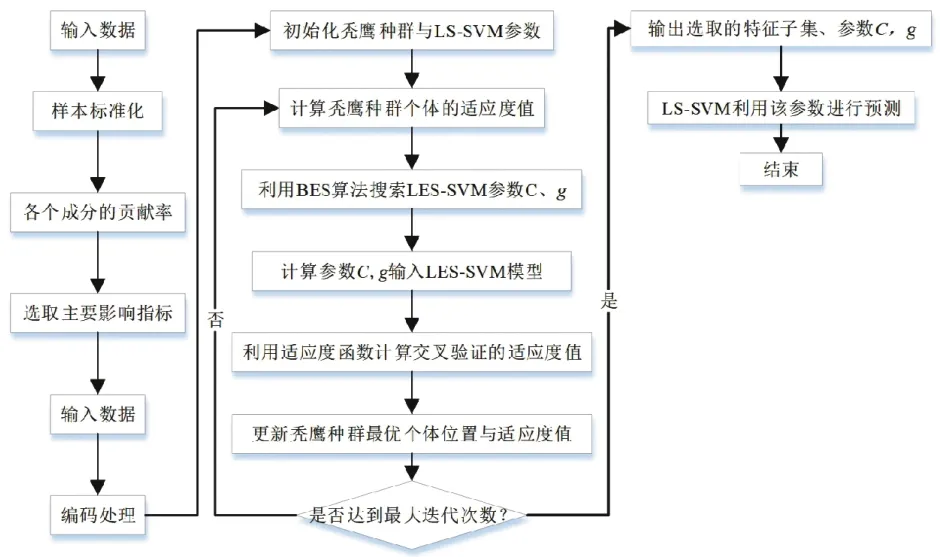
图1 PBES-LS-SVM流程图
具体步骤如下:
(1)选取储能电站电池组的离线数据,提取数据编码、电压、电流、环境温度等重要影响因素后,利用主成分分析对其进行研究。选取主要影响指标,再作为输入数据参与模型的训练。
(2)对数据进行编码处理,初始化秃鹰种群LS-SVM 中的重要参数,惩罚系数C,核函数g等。
(3)计算秃鹰种群个体的位置,进行适应度值的计算,搜索、选取最优的空间。
(4)进入迭代循环,运用BES 算法更新参数。
(5)达到设定迭代次数后,判断目标位置、目标值是否达到最佳,选取惩罚系数C,核函数g。
(6)LS-SVM 运用选取的参数,对锂电池组荷电状态进行预测。
2 数据采集与处理
2.1 数据采集
该研究数据为某储能公司现场采集的锂离子电池组的数据,电池组采用的为120 Ah 磷酸铁锂电芯,一个电池单元为2P16S,即2 个电芯并联形成一个单体电池,再将16 个单体电池串联构成一个电池单元。每个电池单元的容量为240 Ah,额定电压为51.2 V。最终的电池组则是由14 个串联的电池单元,总计224 个单体电池组成,其额定电压为716.8 V。
对电池组数据进行整理清洗后,将异常数据舍弃。选取的因素包括数据编码、电压、电流、温度、环境温度以及电池组SOC的值。在获得的数据中,电池温度、环境温度在一定时间段内变化范围不大,样本数据如表1 所示。
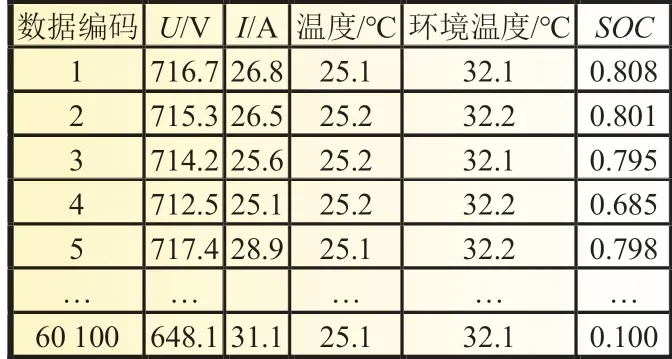
表1 电池组样本数据
2.2 数据处理——主成分分析
PCA 是一种常用的对数据预处理的方法,原理是运用线性代数对原始数据进行降维与因素筛选,该方法可以将多个变量转换为少数几个不相关的综合变量,能够较全面地反应整个数据集。主成分分析的原理公式如式(14):

式中:pR为1 个行向量,表示第R个基;aM为1 个列向量,表示第M个原始数据。
从n个原始变量中取出M个新变量来代替原始数据,其余的n-M变量对于原始信息的贡献率较小可被代替。输入变量越多,对SOC估算的精度越高,与此同时会造成整个模型的收敛性下降。
为减少后续预测模型的计算量,提高整个模型SOC估算的效率,通过PCA 针对表1 中电池组样本数据变量进行综合分析。其中,电压、电流、数据编码、温度以及环境温度为影响电池组SOC预测的指标。针对表1 进行主成分分析的结果如表2 所示。
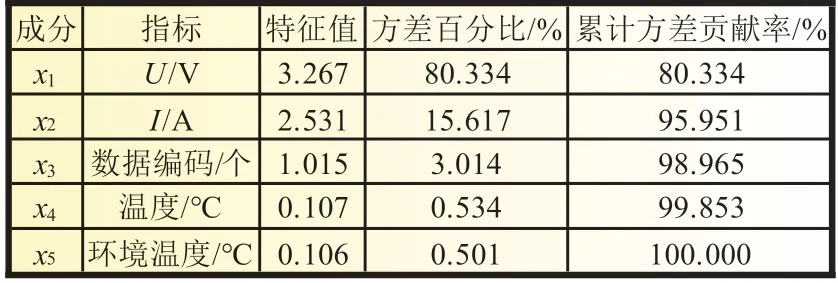
表2 主成分分析结果
主成分提取原则通常按累计贡献率或是主成分特征值提取主成分。根据表2 结果进行选取,成分x1、x2、x3的特征值均大于1,满足特征值大于1 可作为主成分的条件,且所选变量累计方差贡献率大部分大于80%,所以成分x1、x2、x3满足作为主成分的条件,能够反映原始数据中存在的信息。谢思宇等[18]利用主成分分析对NASA Ames 研究中心的电池数据进行分析,得出电池温度对SOC估计的影响呈正相关。但当获得的电池温度与外部环境温度变化范围较小时,利用主成分分析得出的结论为:温度与环境温度对锂电池组荷电状态的影响不大。
因此,选取的成分为电压、电流、数据编码,以此作为输入变量,在减小数据模型规模、维度的同时,消除变量间的相关性,尽可能地保留原始数据所含信息,增强秃鹰算法从现有数据中搜寻最优解的能力。
3 实验结果分析
3.1 参数设定与误差评价指标
秃鹰算法与遗传算法都具有较强的全局搜索能力。关于遗传算法的参数设定为进化代数为100,种群规模为20,代沟为0.9;秃鹰算法优化参数设置为进化代数为100,种群数目为20,优化个数为2。
通过主成分分析可以选取表1 中的电压、电流、数据编码作为输入变量,电池组SOC作为输出变量。针对上述选取的因素进行归一化操作处理,该模型在预测得到数据之后,仍需要进行反归一化处理。归一化公式如下:

式中:yn为表1 中选定因素的原始数据;ymin和ymax为选定因素所有数据中的最小值和最大值;Yn为选定因素归一化操作处理后的数据。
进行归一化处理后,可以避免预测模型在预测时因训练集与测试集量级差别过大,造成预测误差较大的问题。秃鹰算法具备优秀的搜索能力,BES 中的秃鹰将归一化处理后的数据作为模型的参数取值并将经过训练得到的误差作为目标函数,进行迭代寻优,找到最优个体的位置(即惩罚因子C与核函数g)作为最佳学习参数进行回代。LS-SVM 模型应用回代得到的最佳学习参数针对电池组SOC进行预测。
为分析各模型的可行性与有效性,本文主要采用以下4个误差评价标准,即均方根误差(root mean square error,RMSE)、平均绝对误差(mean absolute error,MAE)、平均绝对百分比误差(mean absolute percentage error,MAPE)、仿真运行时长(t)。公式如(16)~(18):
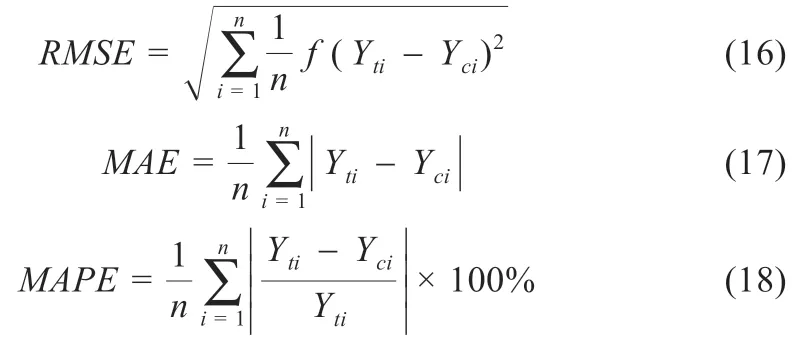
式中:n为预测样本个数;Yti表示第i时刻的实际SOC值;Yci表示第i时刻,模型预报得到的SOC预测值。各模型的仿真运行时长t,利用tic-toc 语句,进行自动计时。
3.2 结果与讨论
为了验证本文提出的PBES-LS-SVM 算法在锂电池组SOC预测方面的有效性。选定锂离子电池组完整的放电数据作为测试集,利用BES-SVM、PBES-LS-SVM 模型及SOC预测研究中常用的算法如GA-BP、GA-SVM 等模型进行独立的SOC预测对比实验。
图2 为各模型的SOC预测结果与真实值的对比曲线。其中,图2(a)为数据驱动以神经网络为基础的预测结果,从图中可以看出,GA-BP 与GA-WNN 预测偏差过大。GA-BP 模型刚开始对SOC进行估计时,该模型的预测值与真实值差距不是很大,拟合度较好,但随着估算样本的增加,预测值有明显的波动情况,个别预测样本的结果逐渐偏离了SOC曲线,误差随之增大。GA-WNN 模型以小波函数代替原有复杂的网络结构,与GA-BP 相比预测效果较好,但拟合效果仍然过差。
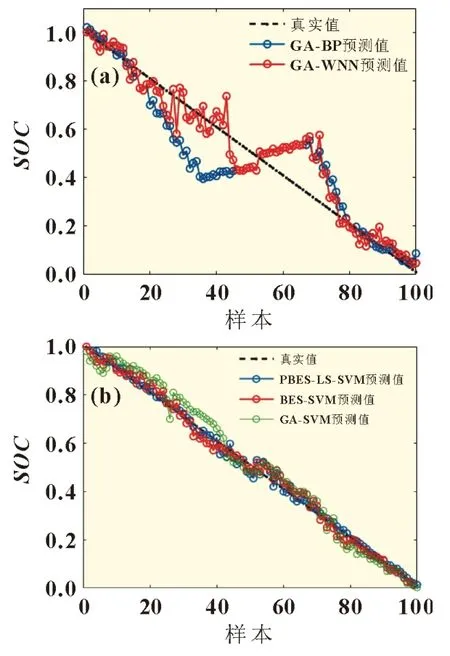
图2 完整放电过程SOC预测结果
图2(b)为数据驱动以支持向量机为基础的预测结果。显然,以支持向量机为基础的三种预测模型,实际误差优于上述两种模型,预测结果更加逼近真实曲线,说明以支持向量机为基础的改进模型更适合用于锂电池组SOC的预测研究中。
从图2(b)中可以看出,PBES-LS-SVM 的SOC预测模型与真实值更接近,表现出良好的收敛效果和预测效果。绝对误差是预测值与真实值存在的实际偏差,图3 为SOC预测模型的绝对误差对比。
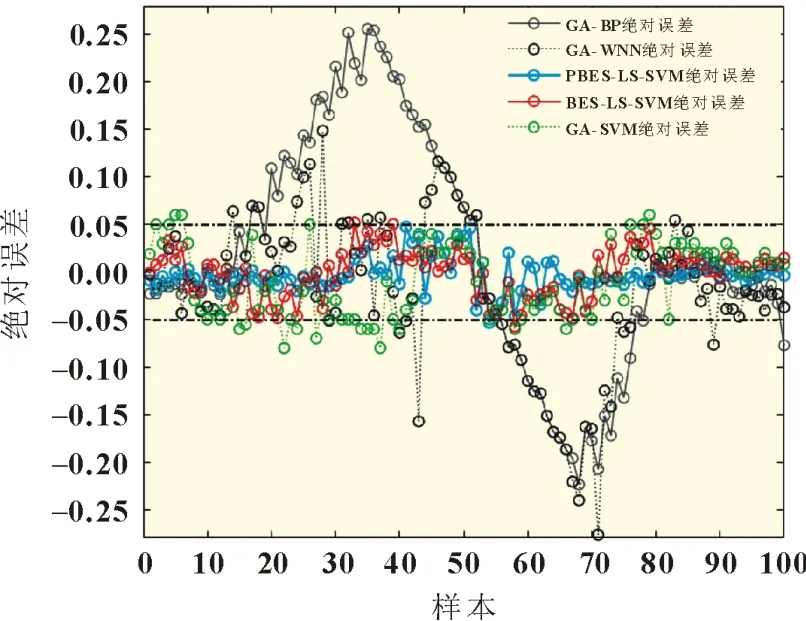
图3 SOC绝对误差对比
从图3 可以看出,BES-SVM 模型的绝对误差处于[-0.060,0.060]区间范围,GA-SVM 的绝对误差处于[-0.070,0.070]区间范围,GA-WNN 与GA-BP 模型预测出现了较大的误差,拟合度较差。而PBES-LS-SVM 模型的绝对误差均处于[-0.050,0.050]区间范围,最大绝对误差仅为0.047。这证明了PBESLS-SVM 模型预测锂电池组放电状态SOC的可行性。
此外,表3 为五种模型的实验指标数值对比。结果显示,PBES-LS-SVM 算法在RMSE、MAE、MAPE和运行时间t四个评价标准下均优于其他算法预测模型,预测性能优越。
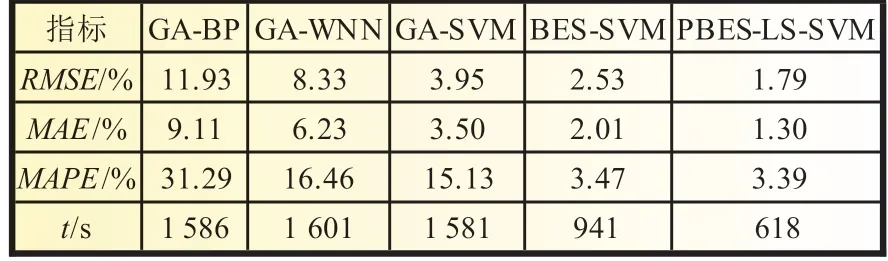
表3 模型误差结果对比
在全放电过程的验证基础上,随机采取部分数据集共10 100 组,验证PBES-LS-SVM 模型在局部放电过程中的预估性能。图4 为各模型预测局部放电过程的结果。
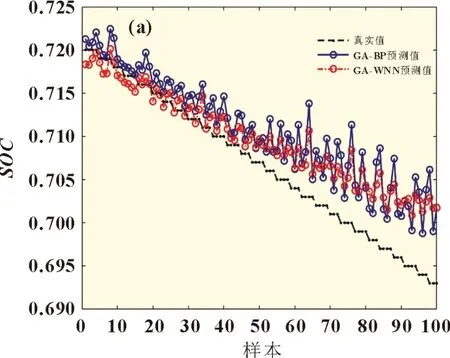
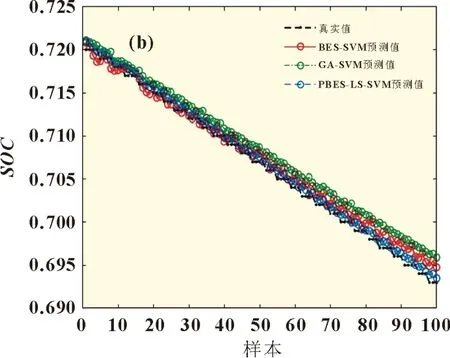
图4 局部放电过程SOC预测值对比
其中,图4(a)为数据驱动GA-BP 和GA-WNN 模型的预测结果,由曲线可以看出,预测值大幅度偏离实际值,拟合效果较差。此外,在仿真过程中发现,以神经网络为基础的数据驱动模型随着仿真次数增加,GA-BP 和GA-WNN 模型的仿真结果变化不大,模型陷入了局部最优解。由图4(b)可知,将PBES-LS-SVM 与BES-SVM 进行对比,利用最小二乘线性系统作为损失函数优化支持向量机,可以提升预测的拟合度。对比GA-SVM 与BES-SVM 模型的预测结果,可以发现:利用秃鹰算法优化支持向量机的预测值与真实值的波动幅度更小。
图5 为各模型100 组的绝对百分比误差。由图5 可知,以SVM 模型为基础的绝对百分比误差均在[-5×10-3,5×10-3]内。其中,PBES-LS-SVM 模型的最大绝对百分比误差为1.6×10-3。仿真表明,被主成分分析优化数据集后的BES-LS-SVM 模型预测结果与实际值拟合程度较好。以锂离子电池局部放电过程数据为基础的模型性能对比,如表4 所示。
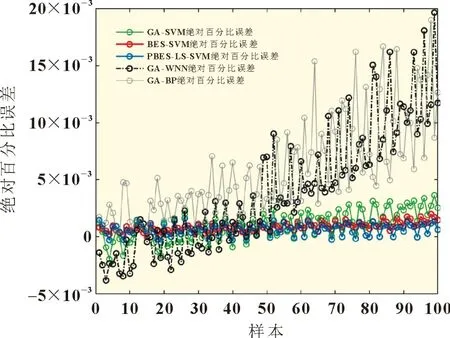
图5 绝对百分比误差曲线图
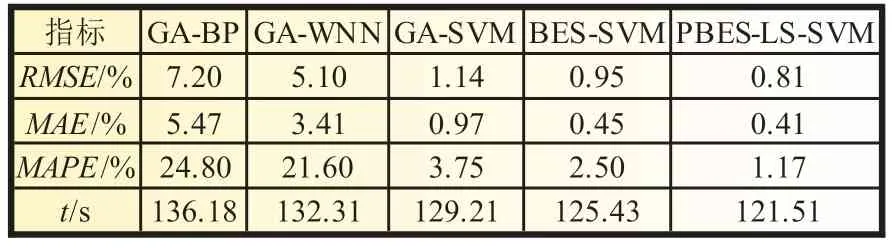
表4 SOC 预测误差对比
表4 记录了PBES-LS-SVM、BES-SVM 等预测模型在面对随机部分数据时的预测误差对比。由图5 和表4 可知,PBES-LS-SVM 模型的RMSE和MAE值最小,分别达到0.81%和0.41%,说明该模型仍保持良好的拟合能力,预测性能较好。
4 结语
为实现准确、快速预测锂离子电池组SOC,避免利用神经网络易陷入局部最优的问题,本文提出一种基于主成分分析和秃鹰算法优化LS-SVM 模型的锂离子电池组荷电状态预测模型。主要结论如下:
(1)利用主成分分析处理数据选取主成分系数较高的因素作为BES-LS-SVM 模型的训练集,可以减小变量间相互影响,提升数据质量。
(2)采用秃鹰算法优化LS-SVM 中的惩罚系数C和核函数g,增强了模型的全局搜索能力和计算能力,提升了SVM 模型的拟合能力。
(3)仿真结果显示,以支持向量机为基础的预测模型更适用于锂离子电池组荷电状态的预测。本文提出的PBES-LSSVM 模型误差低,具有良好的追踪性、快速性和泛化性,能够满足SOC精确估算的工程要求。
