基于信号的锂离子电池热失控故障早期检测

薛金花，王德顺,2，李硕玮，杜净彩

(1.中国电力科学研究院有限公司，江苏南京 210003；2.东南大学自动化学院，江苏南京 210096；3.北京交通大学电气工程学院，北京 100044)

锂离子电池具有能量密度高、工作温度范围宽、寿命长等优点，在储能领域被广泛应用。为满足储能系统对能量和功率级别的要求，通常需要采取串并联成组方式进行使用[1]。但串并联成组方式难以实现每个单体状态的精确估计，电、热滥用或运行环境恶劣等原因可能引起电池组单体内部结构发生改变进而导致热失控事故，因此需要尽早实现对电池潜在故障的准确检测，及时停止电池滥用，避免出现危险情况[2]。

电池故障诊断方法可分为基于模型、基于信号、基于知识三类。Ouyang 等[3]提出一种利用递推最小二乘法估计等效电路模型均差模型参数的微短路检测方法，将电池单体的参数与设定的阈值比较以检测内部短路故障，基于模型的方法可以准确辨识出电池故障，但模型参数辨识需要特定工况，实际运行工况及数据精度难以建立准确的电池故障模型；Sun 等[4]使用香农熵对小波变换后的电池电压进行分析并准确检测出电池连接故障，基于信号的方法无需建立模型，但各种信号分解方法的计算量不同，不同特征对测量噪声敏感度不同，亟须提出可靠且可在线应用的信号处理、特征提取方法；文献[5]利用故障树定性分析电池系统故障原因，再通过小波分析提取故障诊断特征量，建立电池系统故障诊断神经网络，从而实现电池系统的故障诊断，基于知识的方法需要大量准确标注故障类型的数据，且由于部分故障没有被完全理解，基于知识的方法需要更有效的规则来精确检测每个故障。

综上，现有的故障诊断方法均存在一定的局限性，如模型参数难以辨识，缺少可靠且可在线应用的信号处理、特征提取方法，需要大量准确标注故障类型的数据等，难以基于少量实际运行数据在故障早期阶段快速检测出故障。本文提出一种基于信号分解的故障检测方法，将经验模态分解与相关系数相结合在线实现故障的早期检测，与小波变换等信号分解方法相比，经验模态分解计算量较小且无需选取小波基等参数，皮尔逊相关系数适合在线应用[6]，在一定程度上改进了基于信号方法难以在线应用的缺点，更早地实现电池故障检测。

1 锂离子电池热失控过程分析

本文案例一热失控数据源于某锂离子电池组实际运行工况数据，该电池组充电截止电压为4.26 V，在电池组热失控前9 个充电段的最高充电电压均超出4.25 V，热失控前7 日最高温度为33 ℃，未超出正常温度上限，由此判断热失控前电池组电压温度未出现异常。图1、图2 分别展示了电池组热失控前最后一个充放电循环与热失控过程电压、温度曲线，充电制式为分段式恒流充电，充电倍率分别为0.45C、0.3C和0.1C。充电与静置阶段电池组温度传感器测量到的温度均稳定在50 ℃以下，未超过正常温度上限，电压较为稳定未出现异常。

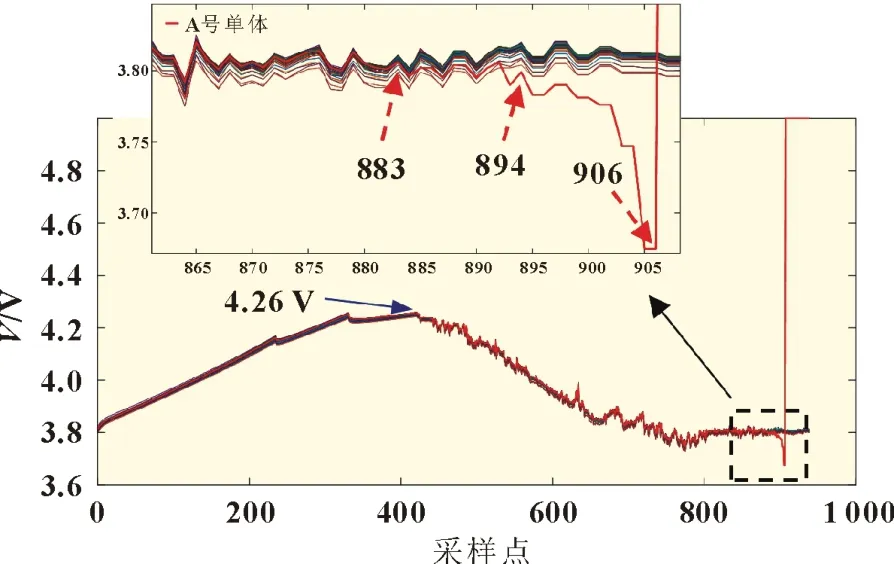
图1 热失控过程电池组单体电压曲线

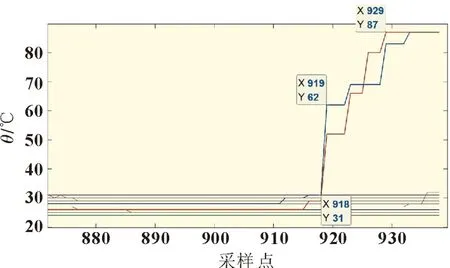
图2 热失控过程电池组温度曲线图

放电段热失控过程分析如下：

(1)在第883 采样点A 号单体电压开始呈现持续下降趋势，此时温度正常；

(2)在第894 采样点前，所有传感器的采集时间间隔为10 s，第894 个采样点后降至1 s，推测此时BMS 检测出故障，此时A 号单体电压下降较为明显，温度正常；

(3)在第907 采样点A 号单体电压上升到5 V，远超锂离子电池正常电压上限4.3 V，原因是采集电路电压上限为5 V，BMS 选择5 V 作为故障状态标志值，此时BMS 检测出A 号单体故障，温度正常；

(4)在第919 采样点与A 号单体相邻的两个温度传感器温度上升，在第929 采样点其中一个温度传感器升至最高温度87 ℃，电池正常工作温度不超过50 ℃，综合之后的电压表现推测此时电池发生热失控。

从BMS 检测出故障(894 采样点)到热失控(929 采样点)经历了大约35 s，35 s 的时间间隔难以采取有效措施抑制电池热失控，因此有必要实现故障快速检测。

本文研究思路如图3 所示。基于以上分析，热失控发生时电压异常表现早于温度异常表现，因此本文主要对电池电压进行分析。由于热失控事故发生在放电段，放电段工况不稳定电压波动较为明显，直接采用相关系数法难以获得准确的结果，因此采用经验模态分解(empirical mode decomposition,EMD)对放电段电压数据进行分解得到稳态分量，再计算相关系数，通过K-means 算法自动辨识故障单体，实现锂离子电池故障早期检测。

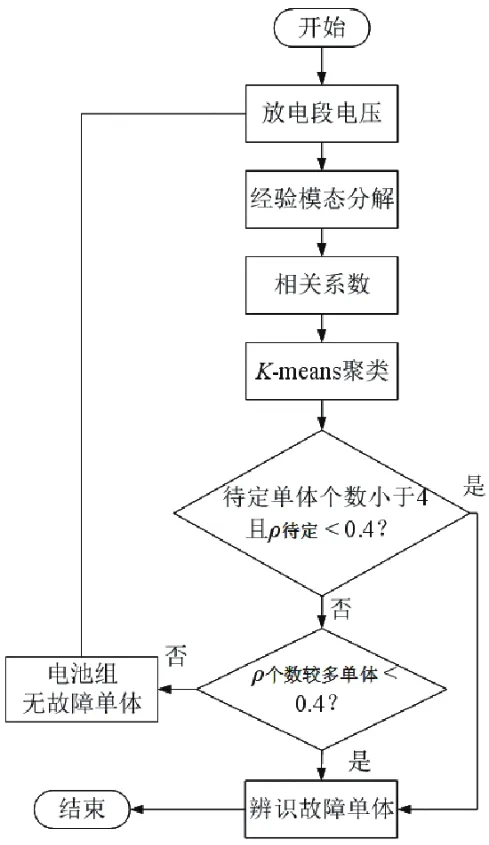
图3 基于信号分解的锂离子电池故障检测流程图

2 基于信号分解的锂离子电池故障检测原理

2.1 经验模态分解

在运行工况中放电段工况不稳定，电池组各单体电压随电流变化而波动，EMD 作为一种自适应信号分解方法，无需设定参数即可实现原始信号的分解，本文采用EMD 算法对放电段电压信号进行分解。

EMD 将原始电压信号分解得到不同特征尺度的本征模函数(IMF)，IMF 需满足以下条件[7]：

(1)IMF 的极值点和过零点的个数差小于等于1；

(2)局部极小值和局部极大值产生的两条包络线之间所有点的均值都为0。

具体步骤[7]为：

(1)获取初始信号x(t)的所有局部极值点，然后通过三次样条线分别将所有极大值和极小值连成上、下两条不同的包络线rmax(t)和rmin(t)；

(2)上、下包络线之间的任一时刻均值记为μ1，从时域信号中减去均值，得到新的时域信号，y1(t)=x(t)-μ1；

(3)判断y1(t)是否满足IMF 条件，若满足则是第一个IMF，若不满足则y1(t)重复进行步骤(1)～(2)的运算，直到满足IMF 两个条件；

(4)计算剩余项q1(t)=x(t)-y1(t)，并作为新的初始信号，重复步骤(1)～(2)，将原始信号分解为n个IMF 分量，直到满足给定的终止条件，得到式(1)：

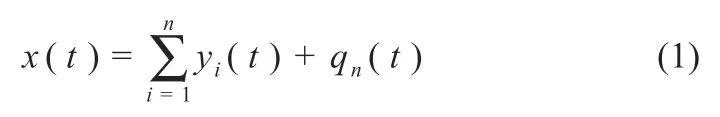
式中：x(t)为原始信号；qn(t)为残余分量，表示信号的平均趋势，信号从高频到低频的不同分量用yi(t)表示。

2.2 皮尔逊相关系数

皮尔逊相关系数是度量两个变量X和Y之间线性关系程度的量，如式(2)所示：

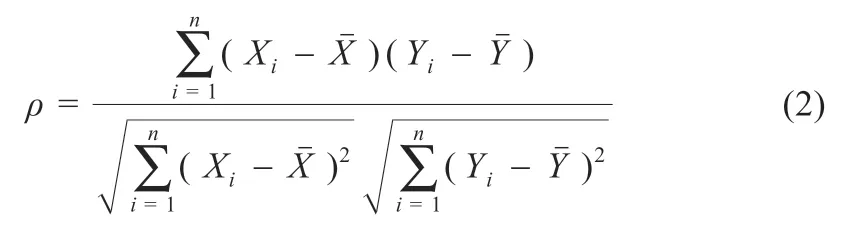
3 基于EMD 与相关系数的故障检测方法

对电池组各单体放电段电压进行EMD 分解，EMD 可以将原始信号分解为若干个不同频率的IMF，本文将最低频分量定义为稳态分量并用于故障检测。

由于BMS 在第894 个采样点检测出故障，为实现故障早期检测，本文选取第424(放电开始)～891 个采样点电压数据，第891 个采样点早于BMS 第894 个采样点26 s，分解电压后得到的电压稳态分量如图4 所示。A 号单体电压稳态分量在第883 个采样点开始出现电压跌落的现象，与原始电压变化趋势相同。在实际应用时，每当单体电压更新，即获取到下一采样点单体电压，使用EMD 分解更新后的电压序列。

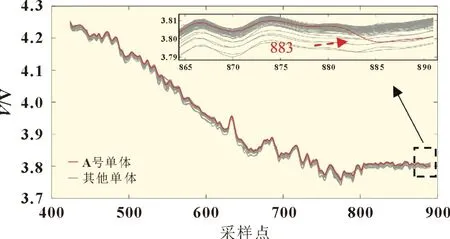
图4 第424～891个采样点原始曲线经验模态分解后稳态分量曲线

在同一工况下，电池组内不同单体的电压响应大致相似，以某只单体的电压曲线为参考基准，将该参考基准电池记为B 号单体，将B 号单体电压分解后得到的稳态分量作为参考分量，求取其余单体的稳态分量与参考分量之间的相关系数，若只有B 号单体出现电压跌落，则所求得的所有相关系数绝对值均应较小，接近于0；若其它个别单体出现故障，则故障单体的相关系数绝对值应较小，接近于0。

此外，运行工况中电压采集误差等原因会造成偶然的电压数据异常波动，为更准确地筛选出电池组中故障单体，采用滑动窗口的方法来避免电压波动所导致的误判。选取时间序列中一定窗口宽度的电压稳态分量作为子序列，本文选取窗口宽度为20，计算每个窗口内B 号单体电压稳态分量子序列与其余单体电压稳态分量子序列之间的相关系数，结果如图5(a)所示。根据2.2 节结论，当相关系数低于0.4 时，两个子序列的相关程度较弱，因此本文将相关系数的阈值设置为0.4。遵循故障单体个数为少数且故障单体极大可能影响相邻两个串联单体的原则，若低于0.4 且异常单体个数小于4，则认定异常单体电压出现异常，可能发生热失控。本案例中A 号单体与B 号单体的相关系数最终下降到0.321，而其他单体与B 号单体的相关系数较大，此时本方法检测出A 号单体电压异常。本文将热失控前的故障报警时间作为量化指标来评价方法的优越性，BMS 在热失控前35 s 检测出电池故障，基于EMD 与相关系数的方法在热失控前61 s 准确检测出故障，相较于BMS 自检，将故障报警时间提前26 s。

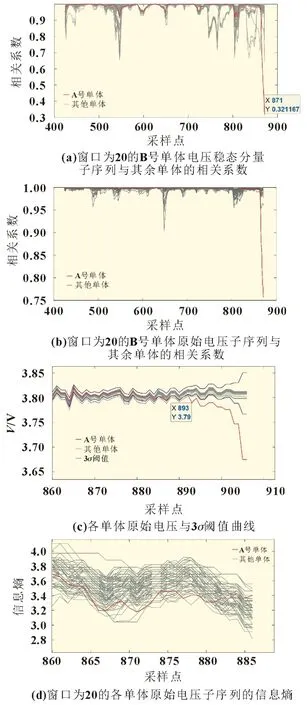
图5 基于EMD 与相关系数的方法与只使用相关系数、信息熵、高斯分布的结果对比

若不使用EMD 分解原始电压数据，直接求取相关系数，结果如图5(b)所示，其中时间序列的长度、窗口宽度保持一致，A 号单体与B 号单体相关系数的最小值为0.77，A 号单体与B 号单体具有强相关程度，难以判断其电压是否出现异常，因此基于EMD 与相关系数方法的准确性优于直接使用相关系数的方法。

为进一步体现本方法的优势，将基于EMD 与相关系数的方法与可在线应用的高斯分布[9]、信息熵[4]进行对比，结果如图5(c)和(d)所示。在图5(c)中，基于高斯分布的方法在第893个采样点检测出故障，虽然其计算量较小，但检测时间滞后于EMD 与相关系数的方法20 s。在图5(d)中，基于信息熵的方法在第886～906 个采样点(最后一个滑动窗口)都未能检测出异常，因此基于EMD 与相关系数方法的准确性优于只使用信息熵的方法，检测时间早于基于高斯分布的方法。

考虑到方法的适用性，若选取的B 号单体出现问题，则求得的所有相关系数均小于0.4，仅依靠阈值的方法会导致极高的误报率，而人工观察的方法难以将此方法推广到大数据分析，同时故障早期检测对时间要求较高，应减小算法计算时间实现故障快速检测，因此采用计算量较小的有监督学习或无监督学习算法。有监督学习对训练样本数量要求较高且有效的故障数据难以获取；而无监督学习不需要训练集，采用无监督学习中的聚类算法并结合相关系数的阈值，确定基于“阈值+聚类”的故障单体智能识别方法。

本文选取无监督学习中的K-means 聚类算法，无需训练集直接对异常单体进行筛选，将K设定为2，根据聚类结果可得到个数较少的一类和个数较多的一类，遵循故障单体为少数的原则，将个数较少且个数小于4 的一类归为待定单体，若待定单体的相关系数均小于0.4 则判断待定单体为故障单体；若个数较多的一类单体相关系数均小于0.4，则判定包含B 号单体在内的个数较少的待定单体为故障单体，进而实现故障单体自动辨识。

由于实际工况故障数据难以获取，且热失控多发于充电及静置阶段，为验证方法的适用性和有效性，本文选取充电过程中热失控案例二作为验证，其电压跌落趋势与案例一相似。

案例二热失控过程电池组单体电压曲线如图6 所示，单体充电截止电压为4.2 V，在第1 619 个采样点C 号单体电压开始呈持续下降趋势，在第1 629 个采样点之后BMS 停止充电，此时模组最高单体电压为4.191 V，未达到截止电压4.2 V，模组最高温度达99 ℃，第1 630 个采样点模组最高温度达113 ℃，推测已经发生热失控。

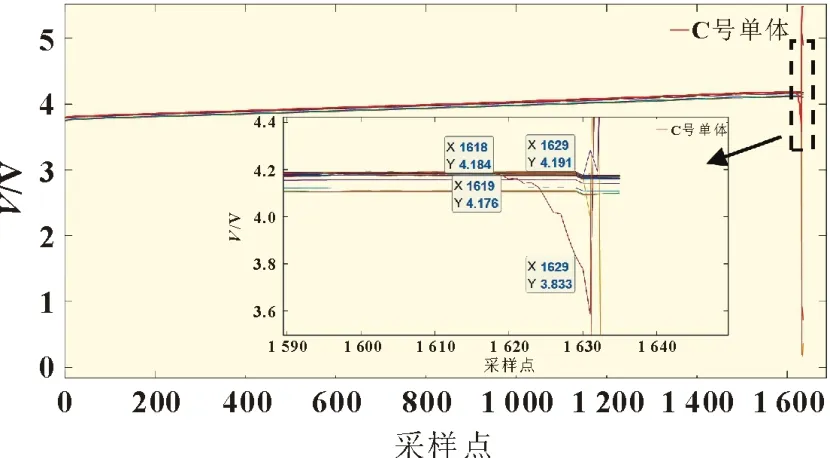
图6 案例二热失控过程电池组单体电压曲线

为实现故障早期检测，本文选取第1(充电开始)～1 619 个采样点电压数据。针对充电电流不稳定导致的电压曲线不平滑问题，采用EMD 对电压序列进行分解得到稳态分量，采用滑动窗口的方法，窗口宽度设为30，计算每个窗口内D 号单体电压稳态分量子序列与其余单体电压稳态分量子序列之间的相关系数，结果如图7 所示。由图7 可知，C 号单体与D 号单体的相关系数最终下降到0.378，小于阈值0.4 且异常单体个数小于4，因此在第1 619 个采样点本方法检测出C 号单体电压异常，需中止充电，此案例中BMS 未能提前检测出电池故障，基于EMD 与相关系数的方法在热失控前11 s 准确检测出故障，说明此方法可以很好地实现锂离子电池热失控故障的早期检测。

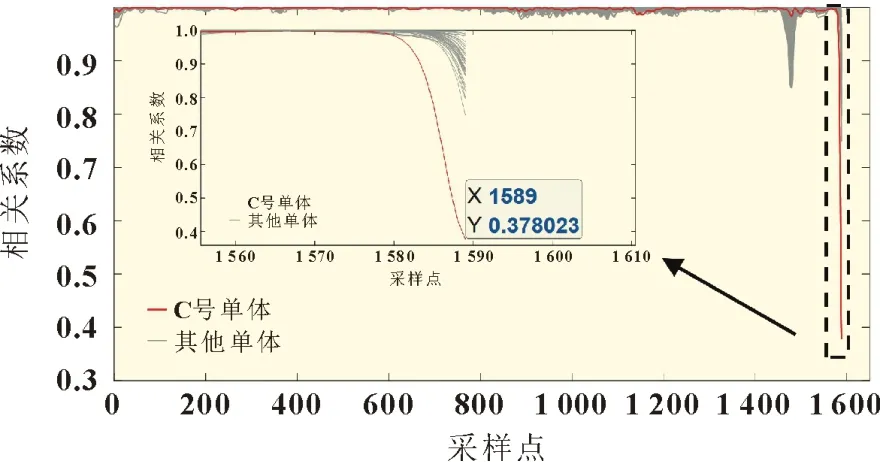
图7 案例二窗口为30的D号单体电压子序列与其余单体的相关系数

4 结论

本文从锂离子电池热失控案例入手，提出了一种基于EMD 与相关系数的电池热失控故障早期检测方法，主要工作如下：

(1)分析了案例一锂离子电池热失控过程，将热失控过程中的电压、温度表现分为4 个阶段，得到热失控发生时电压异常表现早于温度异常表现的结论；

(2)对案例一第424～891 个采样点的放电段电压进行EMD 得到稳态分量，发现A 号单体稳态分量变化趋势与原始电压信号趋势相同，采用滑动窗口计算窗口内B 号单体稳态分量与其余单体之间的相关系数，之后采用K-means 聚类算法实现故障单体自动辨识，最后选取热失控案例二验证方法的适用性。

本文将热失控前的故障报警时间作为量化指标，在案例一中提出的基于EMD 与相关系数的电池故障早期检测方法报警时间比BMS 报警提前26 s，实现热失控前61 s 准确检测出故障，且准确性优于只使用相关系数、信息熵的方法，检测时间早于基于高斯分布的方法20 s，在避免误报的前提下实现故障早期阶段电压异常检测，在案例二中本文提出的方法在热失控前11 s 准确检测出故障，验证了此方法的适用性，此外本方法计算量较小在BMS 中易实现，具有一定的应用价值。在后续的研究中，更多的热失控电池数据将被用于验证本文方法的适用性。