基于岭回归的土壤全氮含量反演模型

徐艺，邵光成*，丁鸣鸣，章二子，何菁

(1. 河海大学农业工程与科学学院，江苏 南京 210098； 2. 南京市水务局，江苏 南京 210036； 3. 江宁淳化街道水务站,江苏 南京 211122； 4. 南京市水利建筑工程检测中心有限公司,江苏 南京 210036)

表层土壤全氮含量(total nitrogen，TN)为氮含量的总和，包括有机氮、硝态氮、亚硝态氮以及铵态氮，还包括部分联氮、偶氮和叠氮等含氮化合物.传统测定全氮含量的凯氏定氮法虽然精度高，然而步骤复杂、成本高，不适用于田间实际应用[1]，而遥感监测具有以下优点：一方面，遥感不需要直接接触观测对象，从而避免对土壤表面作物的伤害.另一方面，可以开展长时间连续监测，而且它的数据可以很容易地集成到地理信息系统中，以便后续进行分析[2].目前，常用的遥感技术包括卫星遥感、无人机遥感、载人机遥感和地基遥感[3-4].相对于其他遥感平台，无人机遥感具有成本低[5]、能获取高空间分辨率影像、适合田块尺度观测等优势[6]，在农情监测中占据了重要位置[7].目前常采用的多光谱反演方法有偏最小二乘法、LASSO缩减系数法、主成分回归等.其中，偏最小二乘回归将关联分析、主成分分析与多元线性回归分析相结合[8]，使用来自响应变量的信息以及预测因子进行特征转换[9]，曾用于热带森林的光谱和化学分析[10]，并作为处理大型高光谱数据集的常用方法[11]，但在采用最小二乘法求解回归系数时发现光谱数据的自相关程度高，存在严重的多重共线性问题，反演结果不可靠[12].杨福芹等[13]基于多重共线性，筛选出对冬小麦氮营养指数相关性较高的图像指数，再利用偏最小二乘法构建反演模型，建模集均方根误差RMSE可达0.085 8，验证集RMSE达0.187 1，预测精度较高；LAURIN等[14]采用偏最小二乘回归(PLSR)，利用高光谱数据与植被指数，对非洲热带雨林生物量进行建模，发现改进后模型精度(决定系数R2=0.70)优于不考虑多重共线性的回归模型(R2=0.64).

高光谱数据通常由100多个带宽为10 nm或更小的连续波段组成，波段之间相关性高，存在多重共线性和“维数灾难”的问题，对反演模型的可靠性造成严重影响[3].为弥补高光谱数据中的多重共线性问题，改善预测模型精度，文中基于无人机多光谱高精度影像，获取其光谱反射率数据，分析农田土壤表层全氮含量实测值与光谱反射率的多元线性回归中的多重共线性问题，构建基于岭回归的无人机遥感影像反演土壤全氮含量预测模型，旨在探索一种兼顾反演精度与光谱数据多重共线性问题的方法，以便为无人机遥感土壤氮素营养诊断提供理论依据.

1 材料与方法

1.1 研究区概况

试验于2021年4月29日在位于南京市江宁区淳化街道某小型灌区插秧前农田进行.该农田位于119°4′0″～119°4′6″E，31°54′11″～34°54′17″N，农田总面积约为6 000 m2，无植被覆盖，有利于观测表层土壤光谱反射率.

1.2 数据采集与处理

1.2.1 数据采集

试验采用棋盘式布点法，选定10块条田，每块再选取6个取样点，每个点位在表土层深度0～30 cm进行取样，并使用紫外分光度计法测定土壤样本的全氮含量，测点分布如图1所示.

图1 采样点分布图Fig.1 Distribution of measurement sampling points

农田遥感影像采用大疆P4 Mulitispectral无人机获取.该型号无人机共搭载6个1/2.9 in CMOS影像传感器，其中1个彩色传感器用于常规可见光(RGB)成像，5个单色传感器用于多光谱成像.单色传感器前滤光片可通过波段：蓝光波段(B)，450±16 nm；绿光波段(G)，560±16 nm；红光波段(R)，650±16 nm；红边波段(RE)，730±16 nm；近红外波段(NIR)，840±26 nm.航拍在4月29日正午11：00—12：00进行，飞行高度50 m，飞行速度5 m/s，规划航点299个，航向重叠率90%，旁向重叠率75%，主航线角度262°，主航线9条，云台俯仰角-90°，共拍摄图片1 794张，采用ArcGIS 10.7对图片进行拼接.该航高下遥感影像的地面分辨率为2.65 cm/pixel，满足精度要求.

1.2.2 遥感影像拼接

精灵4无人机悬停拍摄的图片为带有坐标的TIF格式，将其导入ArcGIS后，指定坐标系为WGS1984，利用ArcToolbox中的“镶嵌”工具进行拼接，最终得到5张不同波段的农田影像.

1.2.3 光谱反射率计算

由无人机拍摄的原始影像数据点为像元值(digital number).为了得到对应波段的地表反射率，后续处理参照《P4 MultiSpectral 图像处理指南》[15]进行.

以求解蓝光波段反射率RB为例(按文献[15]格式)为

(1)

式中：Bluecamera为图像信号值；pCamBlue为相机参数，查遥感图像EXIF中XMP-drone-dji项可得1.355 955；BlueLS为蓝光光强传感器信号值，pLSBlue为蓝光传感器校准参数，两者乘积可直接查XMP-drone-dji下的Irradiance得到，BlueLS×pLSBlue=12 629.98.

Bluecamera可计算为

(2)

式中：IBlue和IBlackLevel分别为归一化到值域[0,1]上的像素值和黑电平的值，其中IBlue计算方式参考式(3)，IBlackLevel可以在遥感图像信息中的EXIF-IFD0-BlackLevel得到，文中IBlackLevel=4 096/65 635=0.062 4；Bluegain为相机曝光时的增益参数；Blueetime为曝光时间.

查图像信息XMP-drone-dji与XMP-Camera项，可得Bluegain=1，Blueetime=0.364.

(3)

式中：DNBlue为蓝光波段像元值.

经过上述计算，可得到土壤样本5个波段的光谱反射率R曲线，如图2所示，图中λ为波长.

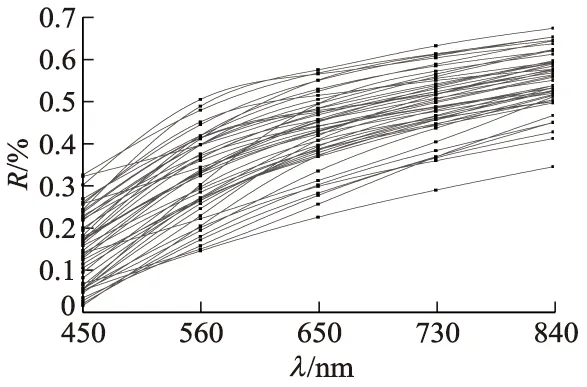
图2 光谱反射率曲线Fig.2 Spectral reflectance curve

2 结果与分析

2.1 多元线性回归建模

假定以式(4)形式的回归模型，反演表土全氮含量，即

TNtopsoil=β1RB+β2RG+β3RR+

β4RRE+β5RNIR+ε，

(4)

式中：TNtopsoil为表土全氮含量，g/kg；RB，RG，RR，RRE，RNIR分别为蓝光波段、绿光波段、红光波段、红边波段、近红外波段的地表光谱反射率；β1—β5为回归系数；ε为残差.

以五波段反射率为自变量，土壤全氮含量为因变量，50组有效数据作为样本，利用SPSS 21.0软件，采用最小二乘回归求解系数β1—β5，结果为

TNtopsoil=-8.437RB+18.310 4RG-28.724RR-
18.569 3RRE+33.995RNIR.

(5)

该模型回归系数R2达到了0.504，然而在显著性t检验中，回归系数均大于0.05，说明多元线性回归系数不具有统计学意义.

2.2 回归系数不合理原因

一般多元线性回归模型可概化为

y=Xβ+ε，

(6)

式中：X={x1,x2,…,xn}为解释变量矩阵；y为被解释变量矩阵；β为待估计的回归系数；ε为残差，满足数学期望E(ε)=0.

依据最小二乘法，回归系数的参数估计值可表示为

(7)

多元线性回归理论假定，参与回归的各自变量间线性无关.若该假设不满足，则会导致模型对误差ε极敏感，回归系数不可靠.然而，当自变量之间存在严重多重共线性问题时，XTX的行列式值接近于0，导致回归系数估计值的解非常不稳定.

由实测反射率数据可得

(8)

使用最小二乘法计算回归系数时，需要使用矩阵XTX的逆，而|XTX|=1.164 6×10-7接近于0，将导致计算出的回归系数过大，且当解释变量发生微小扰动时，回归系数波动剧烈，甚至改变符号.为衡量自变量之间的多重共线性程度，MARQUARDT[16]于1970年提出方差膨胀因子(variance inflation factor, VIF)，计算公式为

(9)

式中：VIFi为对应自变量Xi的方差膨胀系数，i=1,2,…,6.

方差膨胀因子根据式(9)计算可得

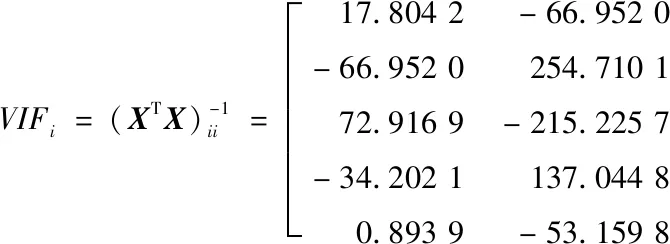
(10)

由式(10)可知，与波段反射率RB，RG，RR，RRE，RNIR对应的方差膨胀因子分别为17.804 2，254.710 1，1 047.716 9，986.509 9，103.774 1.根据HOERL等[17]的研究，当VIF>10时，说明自变量之间存在多重共线性问题；若VIF>100，说明多重共线性现象严重.本次所测量的光谱数据中，有4个波段的VIF在100以上，说明光谱反射率数据存在较严重的多重共线性问题.

2.3 岭回归建模

岭回归是一种在自变量高度相关的情况下估计多元回归模型系数的方法.该理论由HOERL等[18]首次提出.当线性回归模型具有一些高度相关的独立变量时，岭回归为最小二乘估计不精确的一种可靠的解决方案，它通过人为引入惩罚项kIp，回避了XTX行列式接近0的问题，即

(11)

k取值在0到1.当k=0时，岭回归退化为最小二乘估计.由于引入人为误差项，该估计为有偏估计.HOERL等[18]证明，存在k值使得岭回归参数估计值的均方误差小于最小二乘估计，并提出岭迹法以确定合适的岭回归系数；岭迹为所有标准化回归系数与k的曲线图，k∈[0,1].此外，HOERL等[18]提出了4个选择最佳k值应满足的条件：① 岭迹线基本稳定；② 回归系数没有不合理的数值大小；③ 回归系数不再正负波动，符号变得合理；④ 残差平方和相较多元线性回归没有显著增加.

图3为岭迹图及各方差膨胀因子随k的变化图，图中VIF1，VIF2，VIF3，VIF4，VIF5分别表示回归系数β1—β5对应的方差膨胀因子.其中图3a为岭迹图，βs1—βs5为标准化回归系数，是将自变量矩阵与因变量进行z-score标准化[19]后回归得到的系数，分别与回归系数β1—β5对应.由岭迹图可知：① 当k=0时，回归系数βs2，βs3，βs5的绝对值较稳定时偏大，说明βs2，βs3，βs5被严重高估；随着k值增大，βs1—βs5的绝对值都逐渐减小，且趋于稳定.② 随着k值增大，βs2由正转负，最后达到稳定.③ 在k≥0.025之后，标准化回归系数没有不合理的值.

由图3b—3f可知，5个方差膨胀因子均随k增加而迅速减小，当k=0.04时，VIF均小于10，此时可认为多重共线性对预测模型的精度影响较小.

图4为R2、均方根误差与P值随k值的变化情况.岭回归与其他加入人为惩罚项的回归方法类似，模型回归拟合精度会因惩罚因子的增大而迅速降低，因此k不宜设置过大.图4c中P1—P5分别对应回归系数β1—β5的P值，用于评估不同岭回归系数下的显著性水平[20].当P≤0.05时，可认为通过回归系数的显著性检验；当k≥0.12时，P1—P5均小于0.05，此时所有的回归系数都通过显著性检验.

综上所述，当k=0.12时，回归决定系数R2从0.504降至0.408，且此时回归系数趋于稳定，数值合理，各波段方差膨胀因子均小于10，且P值小于0.05，表明所有回归系数均通过显著性检验.因此，取k=0.12作为最佳岭回归参数，此时表土全氮含量估算值可由五波段反射率表示为

TNtopsoil=1.931 6RB-5.308 4RG-10.538 9RR-
0.324 4RRE+13.746 1RNIR.

(12)

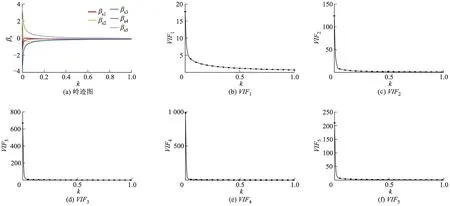
图3 岭迹图和方差膨胀因子随k值的变化图Fig.3 Ridge trace and variation of variance inflation factors with k

图4 R2、均方根误差与P值随k值的变化Fig.4 Variation of R2, root mean square error and variation of P with k

2.4 预测模型评价

图5为拟合结果，图中TNp，TNt分别为土全氮的预测值、实测值.图5a—5b是多元线性回归与岭回归的反演结果.

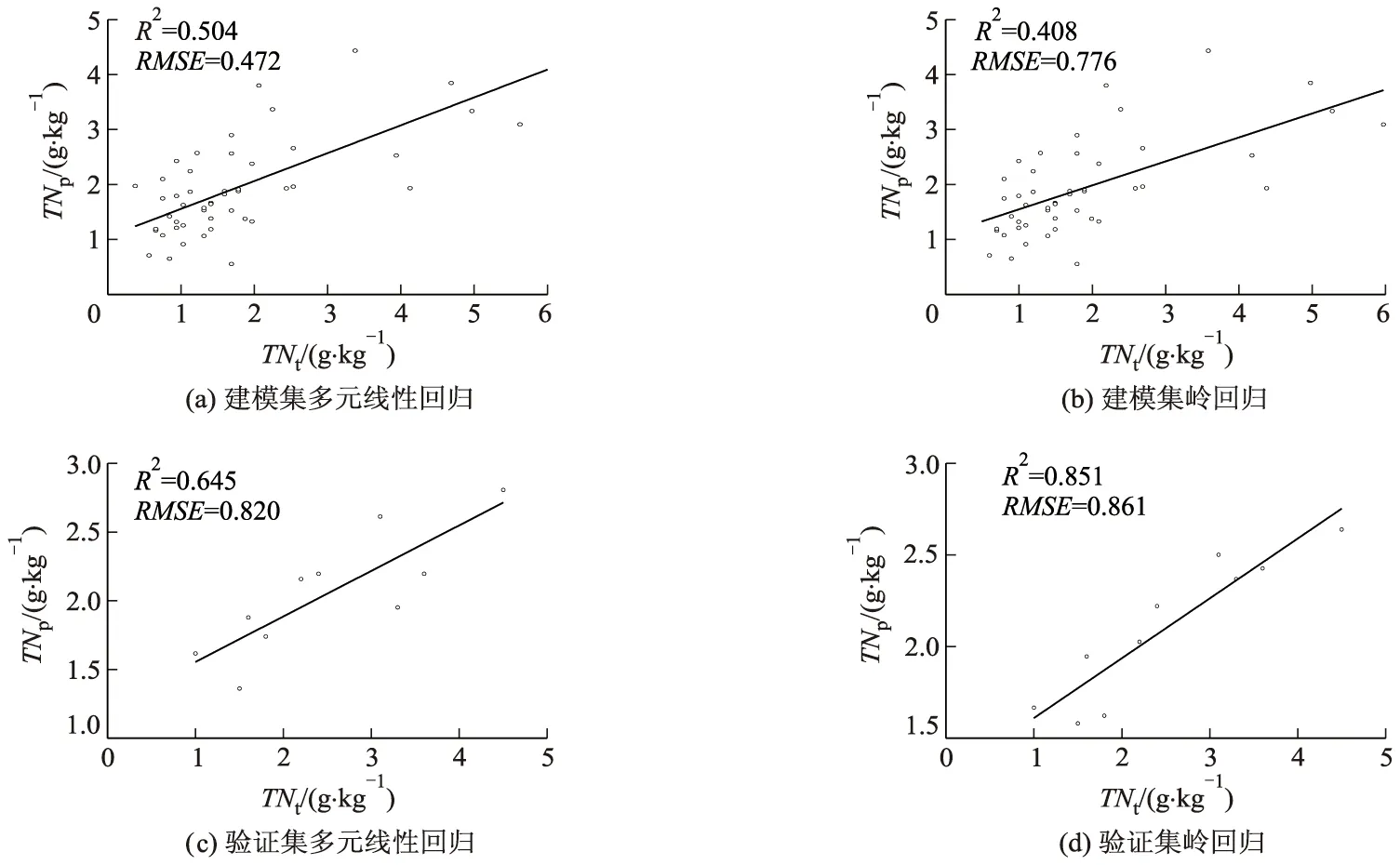
图5 拟合结果Fig.5 Fitting results

多元线性回归反演全氮含量的R2为0.504，均方根误差RMSE为0.472，均优于k=0.12时岭回归预测值；然而由于多重共线性的影响，线性回归在模型预测时表现较差.图5c—5d是利用反演模型对验证集数据进行预测的结果，其中验证集数据由10个条田中各自随机选取1个样本点构成.可以看出，多元线性回归预测模型的R2为0.645，RMSE为0.820，对部分点位全氮含量严重高估，建模效果虽好，但验证效果差.而岭回归预测模型RMSE下降不明显，有较好的预测效果.

通过式(12)并结合农田光谱反射率数据图，可以得到如图6所示的完整表土全氮含量反演结果.利用表土全氮含量分布图，可以快速获取土壤全氮含量信息，对无人机遥感土壤氮素营养诊断和精准施肥具有重要意义.

图6 农田表土全氮含量反演结果Fig.6 Inversion results of total nitrogen content in farmland topsoil

3 讨 论

反演模型中，近红外波段反射率与表土全氮含量的相关度最高.这是因为近红外波段光谱的信息来源于分子振动的倍频和合频，常用于含C-H，N-H，O-H等基团的有机物分析[21]，而土壤中氮素绝大部分为有机结合态，与有机质关联密切[22]，因此高分辨率的近红外波段包含了土壤全氮含量的敏感谱区.利用近红外全谱波段对土壤全氮含量反演可以达到较高的精度.如李颉[23]利用12 500～3 600 cm-1的近红外光谱数据建立的土壤全氮含量偏最小二乘回归模型，决定系数可达到89.63%.利用多光谱数据进行全氮含量反演时，由于土壤全氮含量的取值区间较狭窄，方差较小，不利于稳定预测模型的建立，但通过相关分析，筛选与全氮含量相关性强、显著性高的敏感波段进行建模，仍能达到较高精度[24].

文中研究尝试了利用可见光波段(RGB)与红边(RE)、近红外(NIR)波段光谱反射率数据，在不同岭回归系数下对土壤全氮含量进行预测，其中多元线性回归模型是k=0时的特例.由于上述五波段数据获取便利，虽然模型精度有所下降，但有助于大面积田块全氮含量的快速、定性诊断.综合反演精度与回归系数显著性两方面考虑，选取k=0.12时的岭回归模型作为反演结果.

4 结 论

基于低空无人机搭载多光谱传感器，通过获取表土全氮含量和光谱反射率，研究分析了多元线性回归在表土全氮含量光谱反演问题上的不足，揭示了光谱反射率数据特有的多重共线性问题及其应用限制.通过岭回归方法，以损失一定回归精度为代价，得到一组对多重共线性不敏感的且稳定的回归系数.

研究结果表明，通过表土全氮含量与光谱反射率多元线性回归，发现波段RG，RR，RRE，RNIR对应的方差膨胀因子均大于100，自变量之间存在严重的多重共线性问题.而基于岭回归建模，当k=0.12时，回归R2虽然有所降低，从0.504降至0.408，然而回归系数趋于稳定，数值合理，方差膨胀因子均小于10，且回归系数之间差异具有统计学意义，说明基于光谱反射率信息反演土壤全氮含量的效果较好.但在实践中获取无人机影像进行应用时，还需要综合考虑无人机不同飞行高度而引起的不同分辨率对反演结果的影响.