不平衡电网电压下三相并网逆变器的控制策略分析

程正航，陈泽纯，刘洋，何欢，贺超群

（国网湖北省电力有限公司，武汉 430070）

引言

近10年来，光伏发电事业快速发展，各地光伏发电场的建设装机容量逐年增大，原有光伏发电场的扩建工程也在快速推进。三相并网逆变器的并网控制问题逐渐凸显，使相关研究逐渐深入。因为光伏发电受光照影响较为显著，发电功率日变化曲线明显，所以光伏发电场的光伏电能会在发电场内置电池系统或超级电容系统中存储，使用三相并网逆变器向电网输出持续电能。使用电池系统与超级电容系统联合控制的光储微网系统，有点能量密度高、电容功率密度大的联合优点，同时避免了光照强度变化对其发电功率曲线的扰动，所以被广泛采用。本文重点研究光储微网系统通过三相并网逆变器向不平衡电网进行并网的相关技术。

1 策略设计需求与设计目的

电网正常运行模式下，会出现因为负载不平衡导致电网不对称导致故障型不电压不平衡，可能导致三相并网逆变器出现直流侧电压、入网侧功率出现二倍频脉动，同时导致并网电流快速变化伴逆序和谐波分量，使其并网电流质量受到影响。该作用显著时，可能会损坏三相并网逆变器设备，导致系统保护动作，影响系统的可靠性和安全性。所以，研究光储微网在不平衡电压条件下的主要正序、逆序角坐标系下的PI控制，以及在两相静止坐标系下的比例谐振控制，都属于有效提升光伏发电场三相并网逆变器可靠性和安全性的有效途径。

本文拟设计一套基于功率补偿算法的限流策略MPDPC，当电网电压发生不平衡时，在直流母线电压控制器中投入陷波器，抑制因为交流侧不平衡电压导致的直流侧二倍频波动，并通过该技术对电池组和超级电容共同组成的光伏储能并网系统给出协调控制，实现多目标下的并网控制过程。从理论上讲，该并网策略可以有效抑制并网电流的谐波畸变过程，为证明该效应，本文通过MATLAB对系统进行充分仿真模拟，对该策略的有效性和合理性进行仿真验证。

2 功率补偿与电流限幅验算实验

2.1 功率补偿的验算

对于功率补偿与电流限幅验算实验的过程分析，首先要根据理论入网功率形成功率参考值，与功率实测值之间进行差值计算，从而对开关信号进行优化，实现相关设备的自动投切，进行功率补偿控制。

静止坐标系下的功率理论值计算可写做：

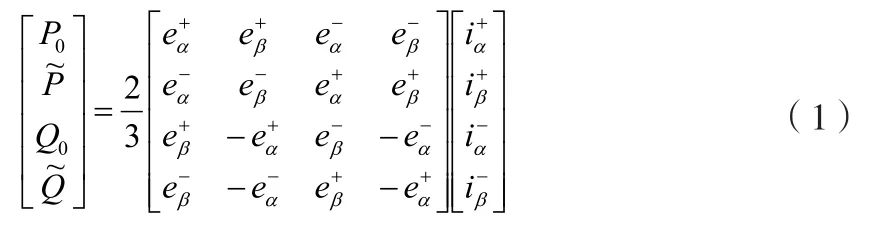
式中：

P0,Q0—有功功率和无功功率的平均值；

—有功功率和无功功率的二倍频脉动值；

—iα的正序分量和逆序分量；

—iβ的正序分量和逆序分量；

—eα的正序分量和逆序分量；—eβ的正序分量和逆序分量。

以充分抑制逆序电流为目标进行功率补偿验算，故可以得到：

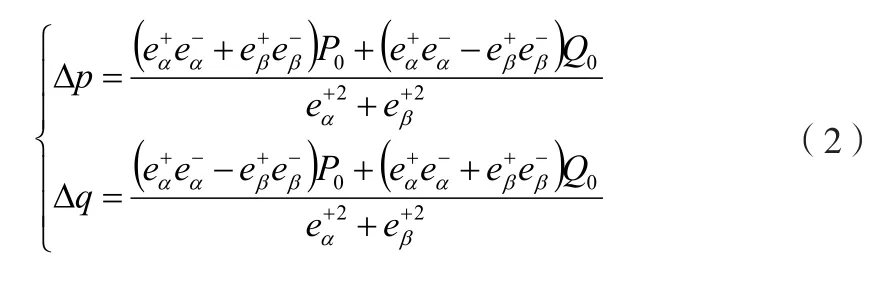
将公式（2）转换为角坐标系，可得：

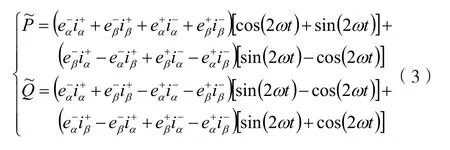
公式（1）及公式（3）属于对有功功率二倍频的抑制补偿，如果进一步考虑对无功功率的二倍频补偿，则有Δp=0且：

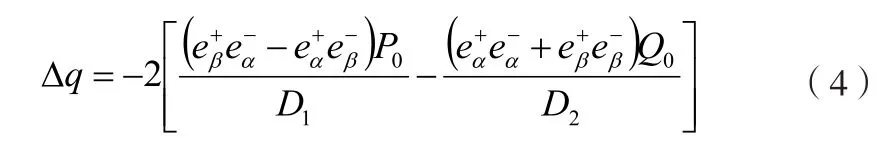
其中：

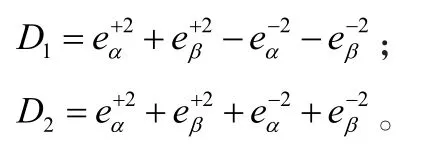
2.2 谐波抑制的参考值验算

电网运行在不同的电压跌落幅度状态时，对不同控制目标的并网参考电流进行幅值预估并对谐波畸变情况进行分析，最终为控制过程提供理论支持和数据支持。

根据前文对并网功率的二倍频脉动进行抑制过程的分析验算过程，对三相电流的参考值进行计算，可得：

其中：

进而得出：

其中：

k取-1值时，可以实现对有功功率脉动的消除，k取+1值时，可以实现对无功功率脉动的消除，k取0值时，可以实现对并网电流的逆序电流进行消除。

2.3 基于MATLAB的仿真分析

假定电网的不平衡度为：

在该电网不平衡度下构建MATLAB仿真环境，赋值Pref=20 kW，Qref=5 kVA，假定三相电压不平衡跌落，C相跌落幅度为B相跌落幅度的2倍，B相跌落幅度是A相跌落幅度的2倍，结合公式（1）至公式（9），可以得到以下仿真结果。

图1中，纵坐标为三次谐波与基波幅值比值，表示并网电流的谐波强度。图2中，纵坐标为故障电流的基波幅值与故障前的基波幅值的比值，表示故障电流的电流异动强度。因为图2仅考虑到基波的幅值问题，没有考虑到谐波的扰动，所以，实际故障电流超出图2的仿真结果。

对比图1和图2，当同时抑制并网功率的二倍频脉动影响时，并网电流中会出现一定功率的三次谐波，且随着电网电压的不平衡性增加，如电网电压的跌落效应趋于严重时，三次谐波的影响更加显著。针对并网电流的幅值，无论采用任何一种控制目标，当电网不平衡性增加是，电网直流部分的谐波现象会显著上升，当电网不平衡性增加到一定幅度时，直流部分电网的过流风险显著增加。过流风险的衍生风险对电网直流部分的电气设备压力增大，可能会造成系统保护动作或设备烧毁。

图1 不平衡度与三次谐波之间的仿真关系

图2 不平衡度与电流幅值之间的仿真关系

综上，使用基于有功功率判断的三相电流峰值参考值限流保护方案是解决该问题的关键突破点，在不发生过流并网过程的同时实现对电网传输最大功率，既确保电网系统直流部分的安全运行，也可以最大限度提升光伏发电场的并网效率，提升其经济效益。在参考电流中引入比例因子的方式对电网并网策略进行安全管控，是本文策略的重要实现途径。

即：

其中：

In—电网未发生不平衡电压时的并网电流；

Imax—iaref2,ibref2,icref2三个故障电流值的最大值。

3 不平衡电网下并网策略的改进策略

3.1 直流母线的电压控制策略

通过接入二、三次谐波陷波器的策略对二次谐波和三次谐波进行管理，可以最大限度解决光储微网中的过流现象。

其传递函数可写做：

其中：

Q—陷波器的选型参数；

ωn—陷波器的特征角坐标频率；

图3中，直流母线中在PI控制器之后布置陷波器，并使用公式（11）的陷波器传递函数进行波形控制，从而使PI控制器的二倍频输出被有效抑制，使直流母线的电流输出更接近参考值。

图3 基于PI控制器联合陷波器的直流母线控制策略图

3.2 逆变器的直接功率控制策略

使用欧拉逼近算法，可以得到k+1时刻逆变器并网功率的预测值：

其中：

H为2×2单位量纲矩阵；

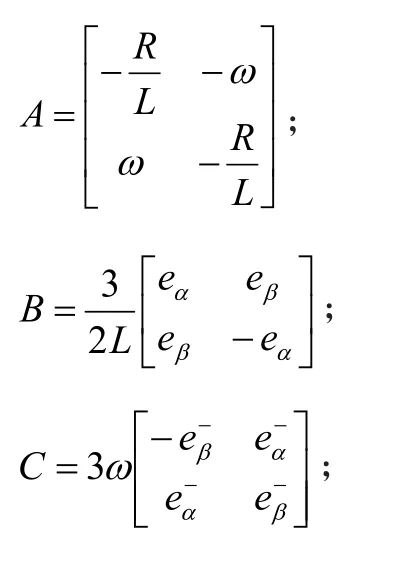
L—电网一侧的滤波电感配置值；

R—并网回路的等效电阻值；

Ts—逆变器控制器的控制周期值；

在上述配置策略基础上引入代价函数，则：

同时，为了避免前文所述多目标控制策略下的控制策略相互影响情况，对有功功率和无功功率的二倍频脉动对正序、逆序电流的影响进行充分抑制，将控制目标进行统一化管理，其管理策略可写做：

该策略中，当k分别取值-1，+1，0时，可以实现对有功功率、无功功率的二倍频脉动的有效控制和对并网电流逆序电流分量的有效控制。

3.3 综合策略汇总

根据前文的推导结果，为了有效平衡电网电压不平衡给光储微网并网过程带来的不确定影响因素，对其有功功率补偿过程使用直接功率控制策略：首先对电网电压延时1/4波形周期获取电网电压的正序逆序分量，确定电网电压的控制目标，获得k值的理论取值，从而选择补偿设备的投切策略。通过对上述8种不同投切状态的预测值变化情况，根据电网和直流侧的实际电压、电流、功率分布情况及其预测值，最终选择最优的解决方案。如图4。

图4 综合策略示意图

4 基于MATLAB的系统仿真实验

4.1 仿真分析的参数设置策略

在对于MATLAB的系统仿真实验分析中，要结合实验过程与实验结果综合利用上述理论分析和策略设计，使用MATLAB对上述策略进行仿真分析，包括对光伏组件、逆变器、HESS等模块进行仿真实验分析。

在光伏电池的仿真模型设计中，设置光伏电池的开路电压为37.2 V，短路电流为8.65 A，当达到最大输出功率时，其最大功率电压为30 V，最大功率电流为8 A，电池模组的串联电池组个数为12个，电池模组的并联数量为8个，每个模组有96个光伏电池，最大功率电压为360 V，最大功率电流为64 A。

在逆变器电网一侧的仿真模型设计中，电网相对地电压有效值为220 V，电网频率为工频50 Hz，并网回路的等效电阻为0.5 Ω，等效滤波电感为10 mH，等效电容为2 000 μF，电网的控制周期设定为15 μs。

在HESS的仿真模型设计中，设置蓄电池的额定电压为360 V，蓄电池的额定容量为100 Ah，超级电容器的额定电压为400 V，超级电容的电容值为50 F，逆变器的电感值为5 mH，逆变器的控制周期设定为15 μs。

光伏电池的光照强度变化趋势按照表1进行设计。

4.2 工况A模式下的仿真结果

工况A模式属于理想工况模式，设定三相电网的电压均为理想电压状态，无功功率为0 kVA，光照强度变化趋势依照表1设定进行配置。

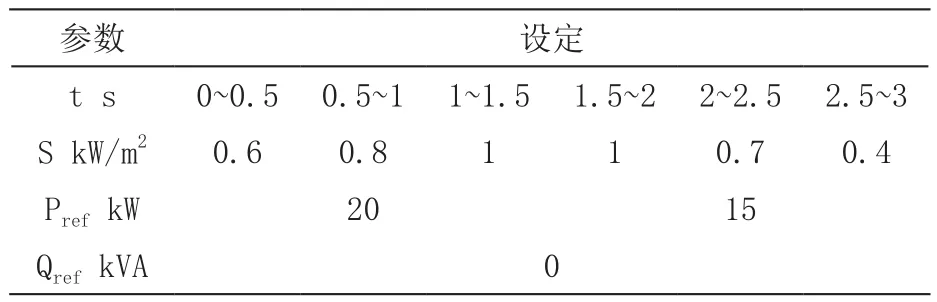
表1 光照强度时间变化趋势设定表

理想工况模式下，并网的有功功率P仅与Pref有关，而此模式下，无功功率Q始终为0，故无功功率Q在实际仿真中始终为0。此模式下，光储微网系统可以根据实际功率输出需求给出相应的有功功率P和无功功率Q，且在实际运行参数发生变化时，逆变器可以快速实现自适应，给出对应的有功功率P和无功功率Q。

当光照强度发生变化时，系统在其变化初期发生一定量的超调现象，但可以快速回归到720 V的目标控制电压下，确保直流母线的运行状态达到最佳状态。储能设施在此调整过程中发挥了重要作用，在超调回调过程中，储能设施特别是超级电容器会快速充放电，以平衡超调对系统带来的影响。

图5为储能设施，包括超级电容和蓄电池组成的光储微网储能系统的充放电波形图，在光照强度发生改变时，系统发生瞬时的超调现象，此时储能设施会对应充放电过程，及时平衡因为系统超调造成的电压不稳定现象。此过程可以有效保护直流母线的稳定性和设备安全。

图5 并网过程的HESS充放电趋势图

图6中可以看到，在20 kW和15 kW的功率参考值模式下，其电流畸变率分别为0.88 %和1.5 %，满足光伏发电场并网要求波形畸变率不超过5 %的行业标准，证明本文策略在实际光伏发电场运行过程中对波形畸变的影响有积极意义。

图6 并网三相电流畸变率变化趋势图

4.3 工况B模式下的仿真实验结果

对于上述的仿真过程分析可以得到在工况B模式下的仿真实验结果，工况B设定为三相电网电压瞬时跌落的工况模式。其光照强度恒定设定为1 kW/m2，并网有功功率Pref设定为20 kW，无功功率Qref设定为5 kVA，在0.2 s之前设定三相电网的电压状态完全正常，在0.2～0.3 s时，A相电压跌落至0.8 pu，在0.3～0.5 s时，A相电压跌落至0.6 pu，在此工况下进行仿真实验。

对于仿真实验结果分析，可知在A相电压两次跌落的过程中，系统可以基本保证有功功率P和无功功率Q的输出稳定性。

当A相电压跌落过程中产生的不同工况条件下，并网的电流畸变率分别达到了7.19 %和15.42 %，该电流畸变已经严重影响到了光伏发电场的并网电能质量。

图7和图8展示了使用了本文策略的仿真结果。

从图7可以看到，在功率变化趋势的仿真实验结果分析过程中，可知在电网电压第一次跌落过程中，无功功率Q的输出发生了一定的超调和自适应过程，而在电网电压第二次跌落过程中，无功功率Q的自适应过程尚未结束，故有功功率P的输出也出现了一定程度的超调和自适应过程。

图7 并网有功功率P与无功功率Q的变化趋势仿真实验图

从图8可以看到，直流母线电压变化趋势仿真实验过程中因为系统的自适应过程导致了直流母线电压并不能稳定在720 V的直流电压上，而是根据系统的超调过程和自适应过程表现出一定程度的波动，但此波动最大稳定在710～730 V之间，即在720±10 V之间，直流母线的电压波动率为＜±1.34 %，在系统的承受范围之内。

图8 直流母线电压变化趋势仿真实验图

该方案牺牲了部分直流母线稳定性和输出有功功率P和无功功率Q的稳定性的基础上，实现了对电流畸变的有效控制。当A相电压跌落为0.8 pu时，电流畸变从未使用本策略时的7.19 %下降到使用本策略后的0.66 %，当A相电压跌落为0.6 pu时，电流畸变从未使用本策略的15.42 %下降到使用本策略后的0.70 %。该电流畸变率小于纯理想状态下因为光照强度发生变化产生的电流畸变率。

5 总结

本文策略的核心思路是采用电流限幅策略，对输电网络电压跌落过程给直流母线带来的扰动过程进行有效控制，特别解决了该过程产生的二倍频谐波对直流母线的影响。通过相关的仿真实验进行分析，并通过引入陷波器及将多控制目标有效综合，在牺牲部分直流母线电压稳定性和输出功率稳定性的基础上，实现对输出电流波形畸变率的有效控制。该策略对提升逆变器工作效率，增加系统的综合稳定性和设备安全性，有积极意义。