实验室对低温试验测量不确定度的评定方法

胡凯，翦文斌，张旺威，张仕彬，黄杰涛

（威凯检测技术有限公司，广州 510663）

引言

测量不确定度是一种合理地赋予被测量值的分散性评定，是定量描述测量结果的一个非负参数。中国合格评定国家认可委员会对检测实验室要求其应有能力对每一项有数值要求的测量结果进行测量不确定度评估。因此，笔者结合GB/T 27418和JJF 1101的两个标准，利用有代表性的1 m³温度试验箱、温度巡检仪进行实际测量，通过对低温参数的测量进行测量不确定度评定，旨在给实验人员对环境试验箱参数的不确定度评定提供参考。

1 温度试验箱的低温参数测量不确定度评定基本步骤

1.1 温度试验箱的低温参数的建模

温度试验箱的实际温度，是依靠人为的观察设备显示值进行记录。以低温参数为例，温度的数学模型公式为T=T1±T2，T表示温度箱内的实际值，T1表示被测设备的示值，T2表示温度的修正值，T、T1、T2的单位均为℃。

1.2 识别环境试验箱的不确定度来源

对温度试验箱的结果测量不确定度来源的识别应从分析测量过程入手。即对温度的测量方法、测量系统和测量程序作详细研究。为此，应尽可能画出测量方法的方框图或测量流程图。因此，温度的测量不确定度可能来源于对被测参数的定义不完善、实现被测温度的定义方法不理想、温度取样代表性不够、对测量过程受环境影响的识别不周全等。

然而，对于不确定度的来源也应进行准确地分类：A类标准不确定度和B类标准不确定度。A类标准不确定度是指在特定的测量条件下通过重复观测值经过统计方法评定的不确定度分量，一般以贝塞尔公式进行计算；B类标准不确定度是指通过非统计分析方法得出的不确定度分量（但B类不确定度不是标准不确定度，必须将B类不确定度转化为B类标准不确定度）。

1.3 对不确定度来源进行识别分类、分析、计算量化

在日常温度试验活动前，应充分对温度试验箱的参数不确定度进行评定。因此，可以先参考计量校准标准JJF 1101-2019先对温度箱的某个参数进行数据采集。其中，要注意针对不同体积的温度试验箱有不同的温度传感器布置要求。将温度试验箱设定目标温度点，在温度稳定后进行读数并记录，每2 min记录所有的温度传感器的温度数值一次，在30 min内读数并记录15次。因此，温度试验箱的参数测量平均值的公式为：

式中：

X—第m个测量点的第n次读数；

x —温度箱内的测量点个数；

y —每个测量点的读数次数。

1.3.1 温度试验箱的不确定度分类

结合温度试验箱的参数建模、数据采集方法、测量仪器的参数等，列举所有影响评定结果的不确定度来源：

1）温度试验箱参数平均值引入的标准不确定度分量u1（即计算所有测量点的标准差），公式如下：

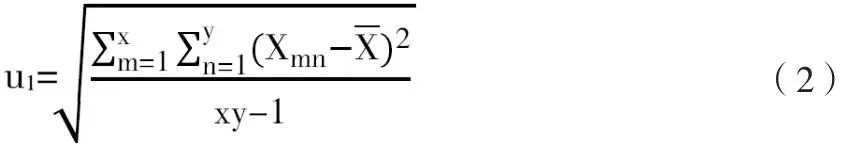
2）温度试验箱在不同测量位置、不同测量时间的温度差引入的标准不确定度分量U2（即抽取具有代表性的测量点计算其标准差），公式如下：

式中：

Ycd—第c个测量点的第d次读数；

a—温度箱内的代表性测量点个数；

b—温度箱内的代表性测量点的读数次数。

以上列举，温度试验箱参数平均值引入的标准不确定度分量u1、温度试验箱在不同测量位置、不同测量时间的温度差引入的标准不确定度分量u2都属于A类标准不确定度。

3）测量设备（温度巡检仪）的分辨率引入的标准不确定度分量u3，可以根据测量设备的分辨率进行计算，公式如下：

式中：

l —温度巡检仪的分辨率；

k —包含因子[1]。

4）温度试验箱的分辨率引入的标准不确定度分量u4，可以根据温度试验箱的分辨率进行计算，公式如下：

式中：

L —温度试验箱的分辨率；

k —包含因子。

5）温度试验箱的温度偏差引入的标准不确定度分量u5，可以根据温度试验箱的温度偏差进行计算，公式如下：

式中：

D+—测量温度的上偏差；

D-—测量温度的下偏差；

k —包含因子。

6）温度试验箱的温度均匀度引入的标准不确定度分量u6，可以根据温度试验箱的均匀度进行计算，公式如下：

式中：

H —测量温度均匀度；

k —包含因子。

7）温度试验箱的温度波动度引入的标准不确定度分量u7，可以根据温度试验箱的波动度进行计算，公式如下：

式中：

W—测量温度的波动度；

k —包含因子。

以上列举，测量设备（温度巡检仪）分辨率引入的标准不确定度分量U3、温度试验箱分辨率引入的标准不确定度分量U4、温度试验箱温度偏差引入的标准不确定度分量U5、温度试验箱温度均匀度引入的标准不确定度分量U6、温度试验箱温度波动度引入的标准不确定度分量U7都属于B类标准不确定度。

2 以低温参数-40 ℃为例对1 m3温度试验箱进行不确定度计算

2.1 计算温度试验箱参数平均值引入的标准不确定度分量U1

利用实验室常规的期间核查仪器温度巡检仪，结合标准JJF 1101-2019校准规范，对1 m3温度试验箱进行数据采样。设定设备目标温度为-40 ℃，在温度试验箱内布置9个测量点（如图1所示）。启动设备并直到温度试验箱保持-40 ℃ 1 h后，对9个测量点进行读数并记录。每个测量点一共进行15次记录，每次读数与记录保持时间间隔2 min。建立温度的数学模型公式为T=T1±T2，T表示温度箱内的实际值，T1表示被测设备的示值，T2表示温度的修正值，T、T1、T2的单位均为℃。

图1 温度试验箱内的布点示意图

通过温度巡检仪进行数据采样，记录的数据如表一所示。根据公式（1）计算表一的数据得出9个测量点的15次数据的平均值为：40.21 ℃，温度上偏差D+为：-1.07 ℃，温度下偏差D-为：-1.11 ℃，测量温度均匀度H为：1.21 ℃，测量温度波动度W为：±0.96 ℃。因此，再根据公式（2）和表1的数据计算温度试验箱参数平均值引入的标准不确定度分量u1=0.572 ℃。

表1 低温参数-40 ℃的9个测量点数据

2.2 计算温度试验箱在不同测量位置、不同测量时间温度差引入的标准不确定度分量u2

重复测量次数在保证足够多的前提下，也应考虑个别随机误差测量参数对不确定度的影响。因此，抽取位置1、位置5和位置8共3个位置的15组数据作为试验箱在不同测量位置、不同测量时间的温度差引入的标准不确定度作为参考对象，如表二所示。根据公式（3）计算表二的数据得出3个测量点的15次数据的平均值为：41.09 ℃。因此，温度试验箱在不同测量位置、不同测量时间的温度差引入的标准不确定度分量u2=1.03 ℃。

2.3 计算测量设备（温度巡检仪）的分辨率引入的标准不确定度分量u3、温度试验箱的辨率引入的标准不确定度分量u4

可根据测量设备（温度巡检仪）的分辨率为l=0.01℃，k=2；温度试验箱的分辨率为L=0.01℃，k=2。所以根据公式（4）和公式（5），分别计算得出u3=0.002 5 ℃，u4=0.002 5 ℃。

2.4 计算温度试验箱的温度偏差引入的标准不确定度分量u5

可根据温度试验箱的上偏差D+=-1.07 ℃，下偏差D-=-1.11 ℃，包含因子k=2。结合公式（6），计算得出u5=-0.545 ℃。

表2 不同测量位置、不同测量时间的温度测量点数据

2.5 计算温度试验箱的温度均匀度引入的标准不确定度分量u6

可根据温度试验的温度均匀度H=1.21 ℃，包含因子k=2。结合公式（7），计算得出u6=-0.302 5 ℃。

2.5 计算温度试验箱的温度波动度引入的标准不确定度分量u7

可根据温度试验的温度波动度W=±0.96 ℃，包含因子k=2。结合公式（8），计算得出u7=-0.48 ℃。

2.6 合成标准不确定度Uc和扩展不确定度Uy的评定

合成标准不确定度Uc==1.42 ℃，而按照统计学中的置信概率p=95 %时，扩展不确定度Uy=2*Uc=2.84 ℃。这就表明当温度试验箱的目标温度为-40 ℃时，通过温度巡检仪记录其平均温度40.21 ℃，此时温度箱内各个位置的平均温度可以表示为=（40.21±2.84）℃，p=95 %。也就通过上述数据说明了这台温度试验箱进行目标温度-40 ℃试验时，箱内的平均温度在（37.37～43.05）℃范围内的置信概率是95 %。

3 结语与建议

本文根据标准GB/T 27418-2017的测量不确定度评定和表示方法、JJF 1101-2019的环境试验设备温度参数校准规范，结合典型体积的温度试验箱的低温实际测量参数进行量化。进而对温度试验箱的不确定度来源进行简单的分析和计算，从而更直观地向读者展现关于温度试验箱的低温测量结果不确定度的评定方法，希望能给读者提供一定的参考价值。

此外，可以看出对于测量结果不确定度的评定，能够有效地为实验室人员把控温度试验箱的质量提供科学的判断依据，也能够让实验室人员全面掌握设备的性能有效性。所以，也建议实验室人员在针对温度试验箱进行期间核查的时候，也可以同时考虑对其进行特定参数的不确定度评定。