基于平滑优化的弹道导弹落点外推方法
2022-11-25靳俊峰刘军伟
代 霞,方 睿,靳俊峰,刘军伟
(1.中国电子科技集团公司第三十八研究所,安徽 合肥 230088;2.孔径阵列与空间探测安徽省重点实验室,安徽 合肥 230088)
0 引 言
随着现代科学技术的不断进步,新型战争武器层出不穷。其中,弹道导弹被誉为“杀手锏”武器,自诞生之初就受到了各国的青睐[1-2]。应运而生地,导弹防御成为各国军事国防领域亟待攻破的堡垒之一[3-4]。
弹道导弹落点外推精度是衡量导弹防御能力的一个重要指标。快速、精确地预报导弹落点是反导雷达研究的重点课题之一,其研究核心一方面在于雷达硬件测量精度的提高,另一方面在于软件系统落点预测算法的优化。
当前比较主流的落点推算方法有2种:一种是数值计算法,建立弹道导弹动力学方程,采用Runge-Kutta数值积分方法,从初始点开始,一步一步外推到落点[5];另一种是轨道解析法,利用一个或多个初始点的位置、速度信息,采用几何方法,计算出导弹轨道参数信息,再通过轨道参数计算导弹落点[6]。
在选取足够小的积分步长的情况下,数值计算法可以达到很高的精度,但计算时间较长,耗费资源较多;轨道解析法计算速度很快,但由于忽略了大气层内空气阻力对导弹的作用,越靠近地球表面,空气阻力越大,因此该方法外推精度较数值计算法要低。当前计算机技术迅猛发展,计算资源已经不足以成为雷达软件系统发展的制约因素,因此数值计算法成为弹道导弹落点外推的优选方法。
在反导雷达工作过程中,落点外推是伴随着点迹更新实时进行的。雷达点迹经凝聚、起始、关联后形成航迹,对航迹进行滤波,最后选取合适的滤波点作为初始点进行弹道外推。外推的精度在很大程度上取决于初始点信息的准确性。
初始点信息的误差主要来自两方面:一方面是雷达测量误差,这是由硬件决定的,不可避免[7];另一方面来源于滤波算法的误差,常用的滤波算法包括最小二乘法滤波和卡尔曼滤波等等。
理论和经验都表明,随着观测时间的推移,航迹关联点迹越来越多,弹道外推精度越来越高,因此实时外推时大多选取航迹最新关联点作为初始点。最小二乘法滤波对于中点的平滑效果最好,在需要进行高精度实时外推时不适用;而卡尔曼滤波器随着关联点迹增多越来越稳定[8]。
针对这两方面的误差,本文提出了一种基于平滑优化思想的弹道导弹落点外推方法,将不敏卡尔曼滤波(UKF)[9]与不敏卡尔曼平滑方法(UKS)相结合,先对关联点迹按时间先后顺序进行UKF滤波,然后对滤波值进行UKS平滑,之后将平滑值按时间从后往前反向排序,对其进行二次UKS平滑,取时间最新的点为初始点进行落点外推,最后计算最新几次外推落点的平均值,作为最终的结果。
利用STK软件进行弹道仿真试验,选取最新关联点作为初始点,分别使用滤波信息和本文提出的方法进行外推,多次试验结果均表明,本文提出的方法能大幅度提高落点外推的精度。
1 基于平滑优化的弹道导弹落点外推方法
UKF是在卡尔曼滤波(KF)的基础上发展起来的一种非线性滤波方法,它利用有限的参数近似反映随机量的统计特性,然后用加权统计线性回归的方法来估计随机量的均值和协方差。
UKF按时间顺序从前向后滤波,利用时间靠前的点迹信息对时间靠后的点迹信息进行优化更新,减小时间靠后的点迹误差。从理论上来说,也可以利用时间靠后的点迹信息对时间靠前的点迹进行优化,从而减小时间靠前的点迹误差,UKS正是这种思想的实现。
1.1 UKF
UKF滤波器的基础是不敏变换(UT)。不敏变换以雷达量测为基础,选取2n+1个δ采样点(其中n为状态向量的维数),并赋予不同的权值W,通过状态方程计算量测向量的估计均值和协方差。
UKF滤波的矩阵表示如下:
(1) 预测
(1)
(2)
(3)
(4)
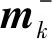
(2) 更新
(5)
(6)
(7)
(8)
(9)
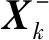
由此,计算得滤波增量为:
(10)
状态向量和状态协方差更新分别为:
(11)
(12)
1.2 UKS
UKS以UKF计算得到的状态向量和状态协方差更新为基础,采用和UKF类似的UT方法,结合状态方程和量测方程进行计算,其第一步和UKF类似:
(13)
(14)
(15)
(16)
(17)

由此计算得平滑增量为:
(18)
状态向量和状态协方差平滑值分别为:
(19)
(20)
用STK软件仿真生成一条理论弹道,时长为100 s,数据率为1 Hz,在距离、方位、仰角3个方向上各加上高斯噪声,形成包含100个点的航迹,以航迹点为基础,按时间先后顺序进行UKF滤波,之后以滤波值为基础,进行一次UKS平滑。
图1是航迹滤波值和平滑值相对理论值的误差。从图中可以看到,无论是从位置误差还是速度误差来看,UKF滤波之后,航迹误差相对量测大幅减小,但在量测点误差出现峰值的地方依然存在较大的误差,经过一次UKS之后,整条航迹变得更平滑,更接近理论航迹。

图1 量测值、滤波值和平滑值误差对比图
1.3 基于平滑优化的弹道导弹落点外推方法
UKS是从时间最新关联点向前进行的,以最新关联点进行初始化,因此没有对最新关联点做平滑,其状态向量和协方差与UKF计算结果相同,如图1中插入的小图所示。为了减小最新关联点误差,提高外推精度,本文在一次UKS的基础上进行了二次平滑。
第2次UKS方向和第1次UKS方向相反,从时间靠前的关联点开始,从前向后进行平滑,将第1次UKS优化后的信息再次传递到最新关联点,减小最新关联点误差。以更新后的最新关联点作为初始值,进行落点外推。图1画出了2次UKS误差的对比图,可以看到,经过第2次UKS之后,最新关联点位置和速度误差均有明显减小。
在雷达工作过程中,航迹长度是不确定的,如果外推时航迹包含n个点,则2次平滑一共需要处理2n个点,当n很大时,处理的时间会比较长,不符合外推的实时性要求;另一方面,外推只需要高精度的最新关联点的信息,作为第1次UKS的首点和第2次UKS的末点,航迹长度不影响平滑过程的的进行。因此,外推时设置合适的窗口宽度,只对窗口内的点进行平滑处理,如图2所示。

图2 基于平滑优化的弹道导弹落点外推方法示意图
利用STK软件进行弹道仿真试验,选取不同的航迹长度,以最新关联点作为初始点,采用数值计算法进行外推。
图3是外推落点误差随平滑窗口宽度的变化图。从图3可以看到,采用本文方法进行落点外推的误差小于直接采用滤波结果进行外推(平滑窗口宽度为0)的误差;随着平滑窗口宽度的增大,落点误差逐渐减小;当平滑窗口宽度小于5个点时,落点误差和采用滤波结果进行外推的误差差别很小,这是因为UKS和UKF类似,几步平滑之后才能稳定;当窗口宽度增大到25时,落点误差已经趋于稳定;再进一步增大窗口宽度,落点误差变化很小,基本保持稳定。因此,在本文的外推示例中,选取25个点作为2次UKS的窗口宽度。

图3 外推落点误差随平滑窗口宽度变化图
在雷达实际工作过程中,每隔一定时间以最新关联点作为初始点进行一次落点外推。由于量测误差的存在,最新关联点可能存在较大的偶然误差。为了降低偶然误差对落点外推精度的影响,计算最新若干(记为p)次外推落点的几何平均位置,作为最终的落点。
综上所述,基于平滑优化的弹道导弹落点外推方法分为以下几个步骤:
(1) 将航迹点按时间先后顺序进行UKF,假设每隔Δt时间进行一次落点外推;
(2) 外推时间到,当前航迹长度记为n,平滑窗口宽度为w。如果n≥w,则取第(n-w+1)个点到第n个点之间(包含2个端点)的航迹进行UKS;如果n (3) 将上一步中经第1次UKS优化之后的航迹按时间反向顺序,进行第2次UKS; (4) 以第2次UKS优化后的最新关联点作为初始点,采用数值计算法进行落点外推; (5) 假设当前时刻及之前外推总次数为m,如果m≥p,则计算第m-p+1次外推落点到当前时刻外推落点的几何平均值;如果m 本文采用STK软件进行仿真试验[10],模拟了一条射程为1 000 km的标准弹道,发射时间为2018年1月1日4点30分0秒,弹道生成函数为Ballistic。导弹发射点经度为127.433°,纬度为39.166 7°,高度为0 m;导弹落点经度为136.452°,纬度为33.843°,高度为0 m。导弹飞行时间为523.7 s,最大飞行高度为284.7 km。雷达站中心经度为136.452°,纬度为33.843°,高度为0 m,数据率为1 Hz。雷达测量误差满足高斯分布,测量精度:距离标准差为100 m,方位角标准差为0.3°,俯仰角标准差为0.3°。 试验中,对理论弹道在斜距、方位、仰角3个纬度分别单独进行加噪,生成了50条模拟弹道,计算过程中取50条弹道计算结果的平均值。模拟过程中从第30 s开始,到第500 s结束,每隔5 s进行一次外推,UKS窗口为25个点,对落点求平均的窗口宽度为12次外推,分别采用UKF结果和本文中的方法进行落点外推,图4为外推落点误差随时间变化图。 图4 弹道外推落点误差随外推时间变化图 从图4中可以看到,总体看来,无论使用哪种外推方法,随着时间的推进,外推落点误差均逐渐减小,和理论分析一致。除了第35 s进行的外推,每一次外推中,采用2次平滑之后的最新关联点作为初始值进行外推的落点误差均小于直接采用滤波结果进行外推的落点误差。 第405 s进行的外推落点误差减小最多,达到23.67%,落点误差平均减小17.16%;第35 s,采用滤波值进行外推的落点误差为74.68 km,采用二次平滑值进行外推的结果比之增大5.97%,为79.14 km。 二次平滑外推后,对最新12次外推落点计算几何平均值,其与理论落点的误差如图4所示。从图中可以看到,除了最开始的几次外推,总体看来,落点平均值误差相对不做平均的结果有大幅减小,减小幅度最大为63.10%,发生在第395 s,平均减小48.00%;对于最开始的6次外推,单次外推落点误差随外推时间推进急剧减小,从92.55 km减小到47.33 km;对外推落点计算几何平均值后,误差反而增大,这与前文分析一致,因此对于这段时间内的外推结果计算平均值时窗口设为1次比较合适(不计算平均值)。 综合以上分析结果可知,在进行常规滤波后,再进行2次方向相反的平滑,以2次平滑后的最新关联点作为初始点进行外推可有效提高弹道导弹落点外推的精度;每次外推后,以最近几次外推落点的几何平均值作为最终的结果,又可以显著提高落点外推精度。 需要注意的是,在本文的弹道仿真试验中,假设雷达量测噪声是符合正态分布的,而对于真实雷达系统来说,该假设并不一定成立。因此,在计算落点的平均值时,可以对每个落点赋予不同的权重,比如对最新外推落点赋予最大的权重,以降低系统误差的非正态性对最终结果的影响。 弹道导弹落点外推的精度在很大程度上取决于初始点信息的准确性,而初始点信息的误差来源主要有两方面:一是雷达测量误差;二是滤波算法误差。 本文针对这2类误差,设计并实现了一种基于平滑优化思想的弹道导弹落点外推方法。该方法在常规UKF的基础上,设置合适的平滑窗口宽度,对窗口内的滤波点进行一次平滑优化;之后再对优化值按时间反向顺序进行二次平滑优化,选取二次优化后的最新关联点作为初始点进行外推;最后以最近若干次外推结果的几何平均值作为本次外推的最终结果。利用STK软件进行弹道仿真试验,结果表明该方法可以有效提高落点外推的精度。 本文方法的核心在于对雷达量测进行常规滤波后,再对滤波值进行2次平滑。这种处理可以显著提高平滑窗口内航迹点信息的准确性,不仅可以应用于弹道外推,还特别适用于雷达事后数据处理。此外,在设置合适的平滑窗口宽度的情况下,该方法也可以应用到雷达实时数据处理中。2 仿真结果
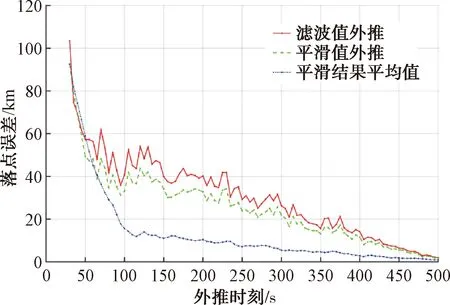
3 结束语
