基于约束最小二乘的稳健发射波束零点控制方法

付 伟，柯 涛，宋 佳，吴 俭

(中国船舶集团有限公司第八研究院，江苏 扬州 225101)

0 引 言

随着数字集成电路技术的重大突破，采用数字T/R组件的有源相控阵雷达能够同时实现发射数字波束形成和接收数字波束形成的功能。相比通过接收数字波束零点控制技术提高雷达抗干扰能力和复杂环境下的目标检测能力，发射波束零点控制技术[1-2]更加能够提高雷达的低截获性能，并且能避免对其他设备的电磁频谱干扰。

对于理想的阵列结构(假设阵元为各向同性的等幅同相理想点源，阵元之间没有相互影响，阵元位置精确已知且没有扰动误差)，文献[3]～[5]采用遗传算法、粒子群优化算法等搜索解空间实现波束的零点控制，存在解的不确定性和不能在线实时计算的缺点。文献[6]～[8]通过求解附加的多点线性约束优化问题获得发射波束的最优权值的解析解。为了提高算法的稳健性，文献[9]～[10]通过最小二乘约束优化来展宽零点。然而，在工程实际中，阵列天线存在互耦效应、阵元通道幅相误差、阵元位置扰动误差、正北标校误差等非理想因素，传统的零点控制算法性能下降，甚至引起波束主瓣产生畸变，以及零点方向不能正确地指向期望方向。因此，研究阵列误差下发射波束零点产生算法的稳健性具有重大的理论意义和工程实用价值。

本文针对阵列误差下稳健的宽零点约束发射波束形成方法，给出了阵列误差已知和未知条件下的最优权值矢量分析。当阵列误差已知时，可首先求解理想阵列条件下宽零点约束的最优权值矢量，然后根据阵列误差矩阵进行修正。当阵列误差精确值不可知时，可首先求解阵列误差条件下无零点约束的常规稳健最优权值矢量，然后通过最小二乘误差逼近求解宽零点约束下的最优权值矢量。数值仿真结果表明，所提方法能够解决阵列误差下宽零点约束发射波束形成的稳健性问题。

1 信号模型

本文以均匀矩形阵列为例阐述稳健的发射波束零点产生方法，应用于均匀矩形阵列的方法同样适用于其他结构布局的平面阵列和立体阵列。

假设空间存在一均匀矩形阵列，如图1所示。

图1 均匀矩形阵列几何坐标示意图

(1)

工程实际中，由于加工工艺误差以及安装误差等因素，阵列天线存在位置误差、通道幅相误差、互耦以及目标指向误差，则式(1)可修正为：

(2)

式中：x′m′n′(t)=s(t-τ′mn)+snoise,mn(t)；aΔmn和φΔmn分别表示通道幅度误差和相位误差;υmn,m′n′表示阵元(m′,n′)对阵元(m,n)的耦合;τ′mn表示带有位置误差和目标指向误差的发射信号空间传播延时，τ′mn=(R+(mdx+dΔxm)u′+(ndy+dΔyn)ν′)/c，dΔxm和dΔyn分别表示x轴方向和y轴方向阵元位置误差，u′=cos(β+Δβ)sin(α+Δα)，ν′=sin(β+Δβ)，Δβ和Δα分别表示俯仰和方位目标指向误差。

将所有阵元发射信号求和，式(2)的矩阵形式可以写为：

y′(t)=wHυgΔ(s+snoise)

(3)

式中：上标H表示矩阵的共轭转置；w表示幅相加权矩阵；υ表示互耦矩阵；gΔ表示通道幅相误差矩阵；s表示阵元发射信号矩阵；snoise表示噪声矩阵。

(4)

(5)

(6)

(7)

(8)

当发射信号s(t)为窄带信号时，s(t-τ′mn)可近似表示为[11]：

(9)

式(3)可另写为：

(10)

式中：dΔ表示阵元位置误差矩阵；v表示阵列导向矩阵，具体表示为：

(11)

(12)

当s(t)表示宽带发射信号时，可采用文献[9]中的方法推广到时域宽带波束形成中，由于篇幅所限，不再赘述。

2 稳健宽零点约束的发射波束形成方法

2.1 阵列误差已知

本节首先给出阵列误差已知的稳健宽零点约束发射波束形成方法。不失一般性，假设目标指向为(u0,v0)，则理想阵列条件下空间合成信号为：

(13)

为了使(u0,v0)方向阵列信号输出最大，常规波束方向图归一化权值选为：

(14)

基于以上最优权值，为了使波束在(ui,vi),i=1,2,…,r方向产生r个零点，采用最小二乘误差逼近建立如下优化模型[11]：

(15)

为求解式(15)的优化问题，利用拉格朗日乘子法得到最优的权值矢量为：

(16)

工程实际中，由于安装误差等因素，存在方位和俯仰角估计误差，目标指向不能精确获得。为了有效避免己方设备间的电磁干扰或防止被敌方截获，在零点附近进行展宽设计，建立如下的优化模型：

(17)

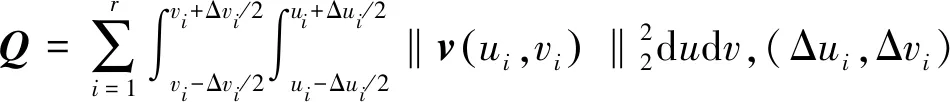
相比于文献[9]，上式减少了r-1个约束，从而增加了阵列自由度，能够更好地抑制干扰。上述最优权值可采用文献[10]中的方法进行求解。

当存在阵列误差时，式(17)的优化模型可修正为：

(18)

式中：E=υgΔ表示误差矩阵。

对比式(17)和式(18)可知，阵列误差下稳健宽零点约束的最优权值矢量wopt满足：

(19)

2.2 阵列误差未知

由于阵元位置误差矩阵dΔ的值随指向变化，或者当阵列误差矩阵的精确值未知时，式(19)不再适用。利用收发天线的互易性求解接收状态下的权值，建立如下优化模型：

(20)

为求解式(20)阵列误差下稳健零点波束最优权值矢量，定义ε=E-I，I表示MxMy×MxMy的单位矩阵，则：

(21)

式中：εmax表示‖εv(u0,v0)‖2的最大值。

从上式可以看出，要使wHEv(u0,v0)=1成立，式(21)需要满足：

(22)

式中：κ1表示小的正数。

式(20)等价为：

(23)

式中：Rn=PHP，表示矩阵的cholesky分解。

更进一步地，式(23)可以表示为二阶锥规划问题，借助凸优化工具箱SeDuMi[12]或者CVX[13]进行求解，如下式所示：

(24)

通过求解式(24)可获得阵列误差下稳健零点波束最优权值矢量。考虑到实际中干扰源位置误差、外界环境影响以及接收通道成本等因素，提出一种次优的求解方法，如下所述。

建立如下优化模型：

(25)

(26)

因为：

wHC-ε′max‖w‖2≤wHEC≤wHC+ε′max‖w‖2

(27)

(28)

所以可建立如下的优化模型：

(29)

3 仿真实验

实验条件设置如下：均匀矩形阵列，阵元数10×10，阵元间距为最小波长的一半，阵列波束指向为(0,0)，期望零点方向(0.5,0.5)，方位展宽0.2，通道幅度和相位均方根误差分别假设为1 dB和10°，互耦矩阵元素假设为υmn,m′n′=0.4|m+n-m′-n′|，阵元位置误差假设服从阵元间距5%的均匀分布。基于以上仿真参数，为了验证本文方法的有效性，进行如下仿真实验。

3.1 阵列误差已知

图2(a)给出了理想阵列条件下常规零点波束方向图。从图中可以看出,波束在(0,0)方向值最大，形成了主波束，在(0.5,0.5)方向值最小，形成了深零点。图2(b)给出了阵列误差条件下的零点展宽波束方向图。从图中可以看出，由于误差的影响，阵列虽然在(0,0)方向形成了主波束，但在(0.5,0.5)方向波束失真严重，未能形成理想的宽零点。图2(c)给出了误差校正后的展宽零点波束方向图。从图中可以看出，通过对阵列误差进行补偿，可在期望零点方向形成理想的展宽深零点波束。

为更直观地展现所提方法的有效性，图3给出了v=0.5时的剖面图。从图中可以看出，常规零点波束方向图仅在方位为0.5时具有深零点，误差校正后的展宽零点波束方向图在u为0.4～0.6之间均具有深零点，而误差校正前的展宽零点波束方向图未能形成较深零点。

图2 零点波束方向图对比

图3 v为0.5时零点波束方向图剖面对比图

3.2 阵列误差未知

图4给出了采用干扰源法形成的波束零点方向图。从图中可以看出，不同的干扰源数量对形成的宽零点波束有很大影响。1个干扰源可在1个方向形成深零点，2个干扰源可在2个方向形成深零点，3个干扰源可在一定的区间范围形成零点，但零点深度受限。4个或4个以上干扰源才能在理想的方向形成展宽深零点波束。在实际应用中该方法会受到测试条件、实施成本以及环境因素等影响，实用性有待商榷。

图4 不同干扰源数的宽零点波束方向图

作为一种次最优方法，图5给出了式(29)求解的权值形成的波束方向图在v=0.5时的剖面图。从图中可以看出，由于受阵列误差影响，在u为0.4～0.6之间形成了低于-35 dB的零点，能在一定程度上提高雷达的低截获性能以及避免对其他设备电磁频谱的干扰。

图5 本文方法宽零点波束方向图

4 结束语

阵列误差下稳健的宽零点发射波束能够有效减小特定方向的发射能量，避免对己方设备的电磁频谱干扰及被敌方接收机捕获，一定程度上提高了雷达的低截获性能。本文分析了阵列误差已知和未知情况下的稳健宽零点波束产生方法。当阵列误差已知时，通过对误差的精确校正可以形成理想的展宽深零点波束。当阵列误差未知时通过远场干扰源法，利用收发天线的互易性可以得到接收宽零点波束权值，应用于发射波束形成稳健发射宽零点波束。针对实际应用场景，本文也提出了一种次最优的宽零点发射波束权值产生方法。仿真分析结果表明所提方法能在一定程度上形成展宽的零点波束，能够改善多设备间的电磁频谱干扰及低截获性能，具有较好的工程实际应用价值。