自溯源光栅标准物质及其应用

邓 晓，李同保，程鑫彬

（同济大学 物理科学与工程学院 精密光学工程技术研究所，先进微结构材料教育部重点实验室，上海市数字光学前沿科学研究基地，上海市全光谱高性能光学薄膜器件与应用专业技术服务平台，上海 200092）

1 引 言

纳米科技研究0.1～100 nm尺度的物质世界，通过操纵原子和分子制造具有特定功能的产品[1］。在21世纪先进制造的时代背景下，纳米科技 涉 及 纳 米 材 料[2-3］、纳 米 电 子 学[4］、纳 米 动 力学[5］、纳米生物学[6］和纳米药物[7］等前沿科技领域，可以说几乎所有现代科学领域的创新和技术进步都离不开纳米科技[8］。

纳米计量在纳米科技中起着信息采集和分析的重要作用。随着原子力显微镜（Atomic Force Microscope，AFM）、扫 描 电 子 显 微 镜（Scanning Electron Microscope，SEM）、透射电子 显 微 镜（Transmission Electron Microscope，TEM）等纳米测量技术的出现，人们得以在纳米尺度研究物质表面原子、分子和几何微观结构。当前，纳米计量需要迫切解决的问题包括[9］：超精密加工中线宽、台阶、膜厚等的测量[10］、纳米材料中的粒子特征[11］、作为纳米科技主要测量和操作工具的AFM，SEM等的特性表征和测量准确度评定等[12-13］。解决上述问题的关键是保证纳米尺度几何量值测试的统一和准确性，即要求纳米测量通过一条连续的、不间断的长度溯源链链接到“米”定义[14］。然而，溯源于“米”定义的计量型或校准型测量仪器要求工作环境严苛，难以满足现场或一般实验室条件下的校准需求。因此，在纳米尺度计量方面急需发展高可靠性测量技术，同时必须建立可溯源的纳米计量传递标准。

2 纳米长度计量传递标准

溯源性是纳米测量中的基础性问题[15］。溯源链的缺失或者长度量值传递过程中的误差积累会导致纳米测量仪器的测量准确性、一致性和可比性降低，从而限制纳米制造的发展[16］。纳米长度计量标准主要包括：线宽、阶高、线纹尺、节距（1D栅）和网格（2D栅）等。标准物质的纳米传递标准一般具备均匀性、稳定性和量值准确统一的特征。因此，建立基于量值统一的纳米级标准物质的长度计量溯源体系，是纳米测量溯源链传递过程（图1）中的关键环节。

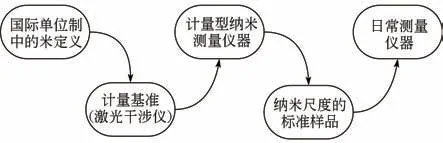
图1 纳米测量溯源性传递链[17］Fig.1 Nano-measurement traceability transfer chain

研制准确适用的纳米节距计量标准主要沿3类技术路线发展[1］。第一类技术路线是继续利用微纳米加工技术刻蚀各种纳米结构。制备纳米标准样板的微纳加工技术主要有：传统光刻技术[18］、电子束刻蚀技术[19］、X射线光刻技术[20］、纳米压印技术[21］和多层膜沉积技术[22］等。然而，基于此路线制备的标准物质不具备溯源性，需要将该标准物质的特征值溯源到国家计量机构计量器具，经过国家计量机构计量定值后，再使用该标准物质校准商用仪器。

第二类技术路线是利用原子晶格研制自然标准。其原理是利用某些表面已知的晶体结构，例如，硅的晶格常数通过X射线干涉仪可以非常准确的测定，因此通过特殊的扫描隧道显微镜（Scanning Tunnel Microscope，STM）或者扫描透射电子显微镜（Scanning Tunnel Electron Microscope，STEM）等制备溯源于晶格常数的标准物质。此技术路线的优势是可以刻蚀10 nm及以下的栅格结构，并且具备自溯源特征，但目前缺乏比较有效的样品循迹方法，同时在刻蚀过程中是否能完美保留原子结构存在巨大挑战。

第三类技术路线是利用激光汇聚原子沉积技术，该技术又称之为原子光刻技术。作为基于原子光学的中性原子束沉积技术，一般有两种方案：金属原子束原子沉积技术和亚稳态惰性气体原子沉积技术[23-24］。金属原子束原子沉积技术利用激光与原子间的偶极力控制原子的运动，从而在基板上制备特定的纳米图案；亚稳态惰性气体原子沉积，使用光抽运作用使原子束形成空间强度分布，进而破坏基板上的特殊膜层形成特定纳米图案。由于激光汇聚原子沉积技术光栅结构溯源于光场波长，因此，此技术路线制备的光栅具备长度自溯源特征。

3 原子光刻技术

原子光刻技术又称为激光会聚原子沉积[25］技术，是一种基于光与原子相互作用，制造一维光栅和二维光栅的技术。一维光栅的节距值由原子的跃迁频率决定，而原子的跃迁频率是一个自然常数，因此，原子光刻制备的一维光栅是一种自溯源节距标准。自原子光刻技术发明以来，学者们已经研制出铬[25］、铁[26］、铝[27］、镱[28］和氩[29］等原子的一维光栅。以铬原子为例，一系列不同节距的一维光栅已经成功研制，例如衍射法测得光栅的节距不确定度为0.006 9 nm[32］，与计算得到的节距不确定度0.004 9 nm基本符合[32］。制备二维原子光刻光栅的方法有二维驻波场原子光刻[33］和分步沉积原子光刻[34］，分步沉积原子光刻制备的二维原子光刻光栅两个方向的节距相等，可以形成对角线完全垂直的菱形结构，因此，分步沉积制备的二维原子光刻光栅是一种自溯源角度标准。同济大学制备的二维铬自溯源光栅的正交角度经德国PTB测量，得到的不确定度为0.003°与计算值0.002 7°基本一致[34］。

3.1 原子光刻技术原理

原子光刻基于激光和原子的相互作用，激光和原子相互作用产生的力分为自发辐射力和偶极力，因此原子光刻技术的主要制备原理为：（1）利用自发辐射力对铬原子束进行激光冷却；（2）利用偶极力对铬原子束进行激光会聚形成光栅结构。

3.1.1 激光冷却

在原子光刻光栅制备中，激光冷却时激光与原子相互作用的力为自发辐射力[25］。设一个光子的动量为P=ℏk=h/λ，ℏ为约化普朗克常数，k为激光的波数。当速度为v的原子与动量为ℏk的光子相遇时，由于两者动量方向相反，原子在吸收该光子后速度降低ℏk/m。为进一步吸收光子，原子需要自发辐射光子回到基态，由于自发辐射光子方向随机，自发辐射累计总动量为0。因此，经过N次受激吸收与自发辐射过程后，原子总动量变化为Nℏk，并且方向沿激光的传播方向，从而可以对原子进行减速，这就是利用自发辐射力对原子横向减速冷却的过程。

3.1.2 激光会聚

激光会聚原子的过程可以看作是激光驻波场的物化过程，激光驻波场中的原子受到交变电场的感应产生振荡偶极矩。该偶极矩与电场相互作用，感受到与电场强度梯度成正比的偶极力。根据半经典理论，偶极力可表达为：

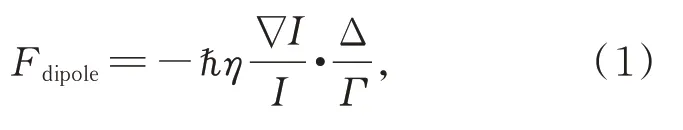
其中：η为能级跃迁几率，Γ为原子的自然线宽，I为激光驻波场的光强。偶极力与光强度的梯度成正比，因此偶极力亦称作梯度力。红失谐情况下，偶极力方向朝着∇I的方向，原子向光强度较大的方向移动，激光驻波场中原子会聚在波腹位置处；蓝失谐情况下，偶极力方向与∇I相反，原子向光强度较弱的方向移动，激光驻波场中原子会聚在波节位置处。

3.1.3 原子光刻光栅的自溯源特性

原子光刻中驻波场的物化过程如图2所示。以铬原子光刻为例，激光能与铬原子作用的前提是激光的频率与铬原子能级跃迁的频率相等，而铬原子7S3→7P40跃迁频率的自然线宽为（2π×5）MHz，与自身跃迁频率705 THz相比可忽略不计，因此铬的7S3→7P40可以看作一个自然常数。原子光刻光栅的周期为激光波长的一半，因此，其节距能溯源到自然界常数。

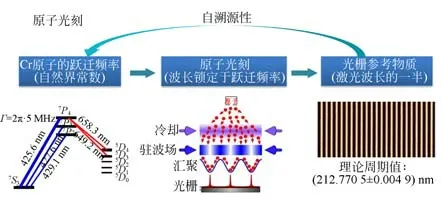
图2 原子光刻光栅的自溯源特性Fig.2 Self-traceability characteristics of atom lithography grating

3.2 一维铬自溯源光栅的制备

同济大学采用自主搭建的原子光刻2.0系统制备一维自溯源光栅，系统实物及光路如图3所示。根据原子与光的作用顺序，铬原子的产生可以分为铬原子束的形成、激光稳频、激光冷却和激光会聚4个部分。这些相互作用的过程均在高真空环境中。激光波长为425.55 nm，对应铬原子的跃迁谱线为7S3→7P40。

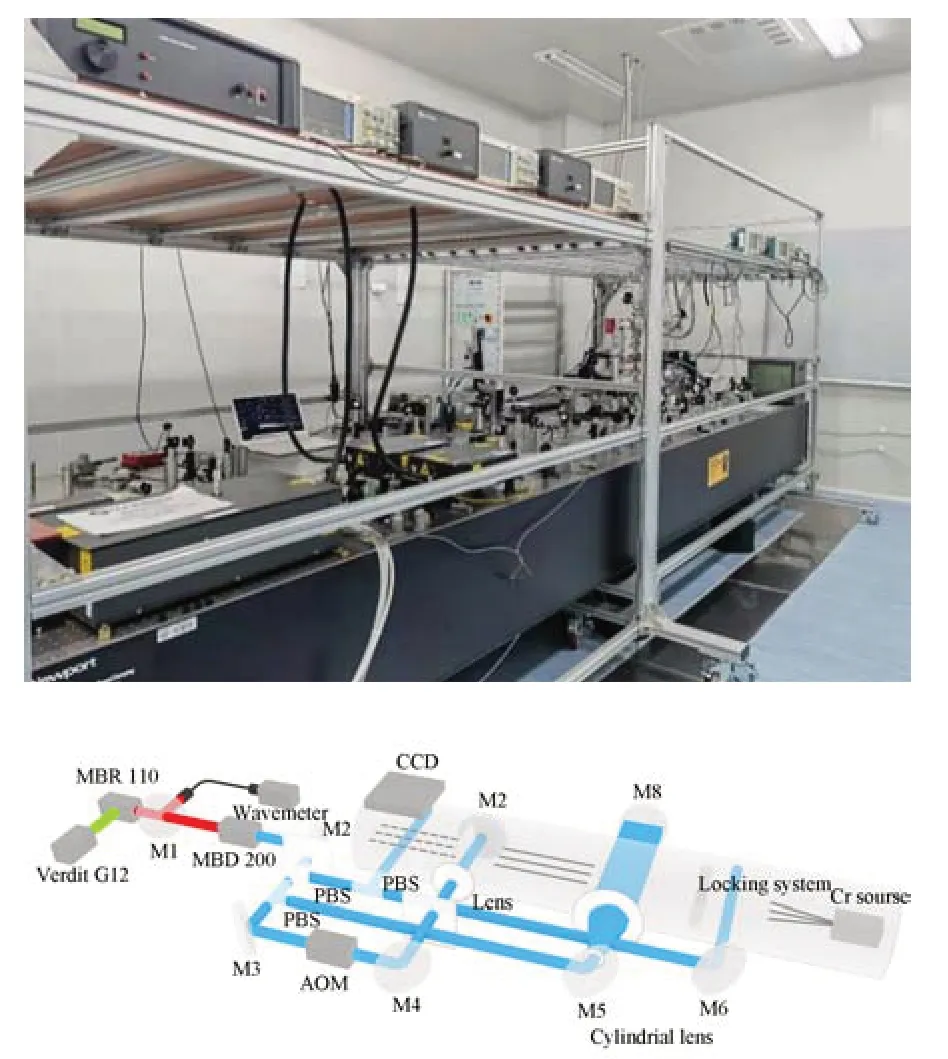
图3 同济大学原子光刻2.0系统及其光路Fig.3 Atom lithography 2.0 system of Tongji university and its light path

3.2.1 铬原子束的形成

在激光会聚原子沉积实验系统中，使用机械泵与分子泵结合的方法可实现高真空（真空度处于10-5Pa量级以上），然后在真空系统内部将金属材料加热至升华状态，并以泄流方式引出金属原子束铬。

3.2.2 激光稳频

原子在近共振激光场中时，因多普勒效应会吸收一定频率范围内的光子，这就是光感生荧光现象。实验中利用激光感生荧光的现象，设计了一套系统实现激光穏频[35-36］。某一激光频率下产生的荧光，通过4f成像系统清晰地成像在二象限光电探测器上，光电探测器将接收荧光的亮度转为电信号，在上下两块探测器上产生两个电信号。稳频电路对这两个信号进行放大后差分处理，处理后的结果反馈至激光器MBR，MBR调整自身的输出频率，就能将激光频率锁定在原子跃迁频率附近。目前，频率稳定性优于0.26 MHz[37］。

3.2.3 自溯源光栅准确性

同济大学纳米计量课题组研制的一维212.8 nm自溯源光栅在2021年成功获批了国家一级标准物质（编号：GBW13982），标准物质证书如图4所示。为验证自溯源光栅的准确性，随机挑选了2个样品到德国联邦物理技术研究院（PTB）进行测量定值，测量结果见表1。由表1可知，任意两个自溯源光栅平均节距的差异为0.001 nm，不确定度为0.008 nm，具有极高的均匀性和一致性。

图4 一维212.8 nm铬光栅国家一级标准物质定级证书Fig.4 Gradation certificate of national certified first-class reference material of one-dimensional 212.8 nm chromium grating

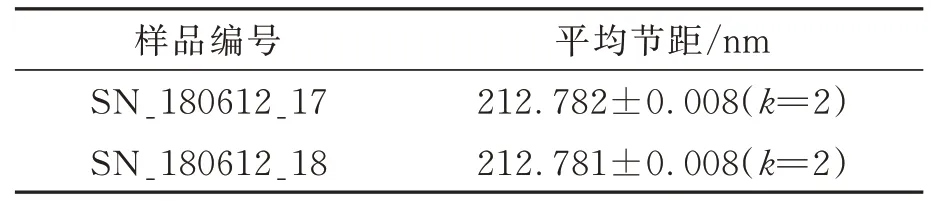
表1 自溯源光栅在PTB的测量结果Tab.1 Self-traceable grating measurement results in PTB

3.2.4 一维自溯源光栅的应用

由于一维铬自溯源光栅节距能到达皮米级，因此，一维铬自溯源光栅在校准现代精密测量仪器有很广阔的应用前景。以一维铬自溯源光栅校准AFM[12］为例来说明自溯源光栅在校准现代精密测量仪器的应用。以212.78 nm节距为标准，通过扫描不同大小的区域，如表2所示，用重心法计算出AFM扫描出来的平均节距与标准值对比，从而表征AFM扫描图的非线性误差。

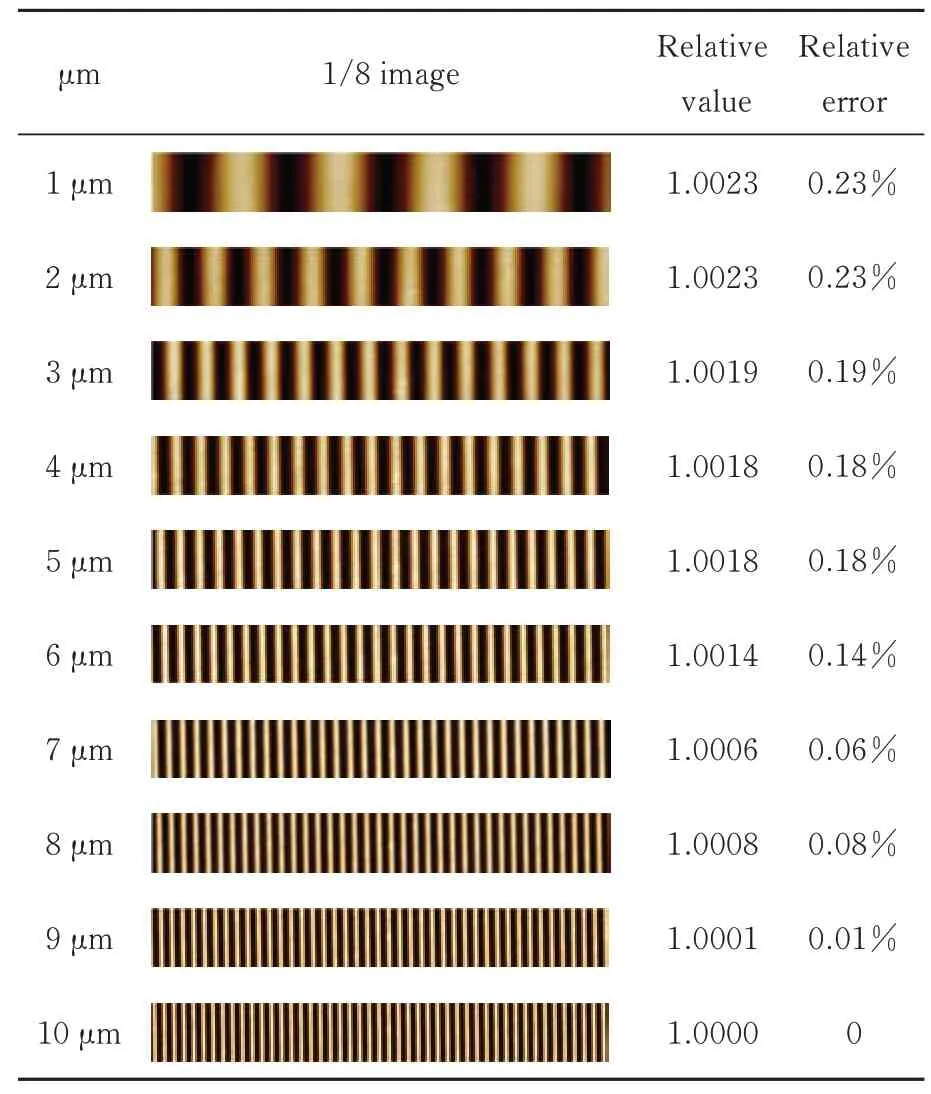
表2 AFM扫描不同面积的自溯源光栅的非线性Tab.2 Nonlinearity of a self-traceable raster with different areas by AFM

3.3 大面积一维铬光栅的实验制备

原子光刻光栅具备自溯源特征，准确性与一致性极高。以铬原子光刻光栅为例，周期为212.78 nm的一维自溯源铬光栅经验证准确性与一致性均在0.001 nm量级，极高的准确性对于精密仪器校准具有重要意义。然而，原子光刻光栅结构面积受到激光驻波场和原子束的限制，导致其应用受到限制。1993年，McClelland等制备的铬原子光刻光栅面积为0.4 mm×1 mm[25］。1995年，Gupta等制备的铬原子光刻光栅面积为0.1 mm×0.2 mm[33］。1997年，Drodofsky等制备的铬原子光刻光栅面积为0.16 mm×1 mm[38］。2004年，Myszkiewicz等制备的铁原子光刻光栅面积为0.4 mm×1.6 mm[39］。2012年，邓晓等制备的铬原子光刻光栅面积为0.7 mm×1.8 mm[40］。2018年，张彤等利用激光扩束的方法，把圆形激光整形扩束为椭圆激光，铬原子光刻光栅面积增加到1.5 mm×1.5 mm[41］。但由于原子光刻对驻波场功率密度有一定的要求，激光扩束的方法存在很大的局限性。

原子光刻光栅的面积直接由激光驻波场决定，激光会聚原子根据激光的功率密度不同可分为3种模型：薄透镜模型，厚透镜模型，以及沟道化模型[42］。其中，沟道化模型的功率密度要求最高，这种激光会聚原子模型的节距最精确，光栅的半高宽最小，线边缘粗糙度最低。由于功率密度的要求限制了驻波场的宽度，原子束的发散角限制了光栅驻波场方向的长度，因此需要拓展自溯源光栅的面积。

3.3.1 扫描原子光刻

为了解决自溯源光栅高斯方向宽度受限的问题，本课题组提出了扫描原子光刻技术[43-44］，其基本原理如图5所示。由激光会聚原理可知：原子会聚于驻波场的波腹（红失谐）或者波节处（蓝失谐），光强I可以表示为[45］：

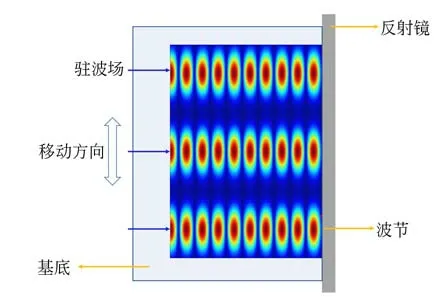
图5 扫描原子光刻原理[44］Fig.5 Scanning atom lithography principle

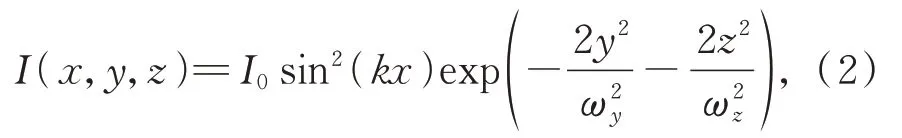
其中：激光入射方向为x负方向，I0为驻波场波腹处的光强，ωy为高斯激光y方向的束腰半径，ωz为高斯激光z方向的束腰半径。由式（2）可知，x=0时，即反射镜的表面处有I(x，y，z)=0。因此，反射镜的表面始终是驻波场的波节，当上下扫描驻波场时，不同位置的光栅线是完全重合的。通过在真空系统外的道威棱镜来扫描驻波场，在保证驻波场功率密度的同时实现操作的可行性和便捷性。目前，使用扫描原子光刻的方法将原子光刻光栅的高斯方向宽度从0.25 mm扩展到1.5 mm（见图6）。扫描原子光刻技术在保持光栅线完全重合的同时，保证自溯源光栅的均匀性。

图6 扫描原子光刻光栅10μm×10μmAFM图像以及光栅峰谷高度在高斯方向的分布[44］Fig.6 Scanning atom lithography grating 10μm×10μm AFM image，and peak to valley height in the Gaussian direction

3.3.2 拼接原子光刻

为了解决自溯源光栅驻波场方向长度受原子束和发散角限制的问题，本课题组提出了拼接原子光刻技术[44］，如图7（a）所示。

图7 （a）拼接原子光刻示意图；（b）拼接原子光刻原理；（c）两次拼接原子光刻光学像和P1～P7的AFM图像；（d）驻波场方向上光栅的峰谷从左到右的高度分布[44］Fig.7（a）Schematic diagram of splicing atom lithography；（b）Splicing atom lithography schematic；（c）Two splicing atom lithography optical images and AFM images of P1 to P7；（d）Peaks to valleys height along grating in direction of standing wave field from left to right

拼接原子光刻的原理和扫描原子光刻的原理相同，同样是利用形成驻波场的反射镜表面始终是驻波场的波节这个关键结论，在进行一次原子光刻之后，移动相对固定的反射镜和基底一段距离，使第二次原子光刻和第一次原子光刻有部分重叠；然后，保持实验条件和第一次完全相同的条件下进行第二次原子光刻，可根据需要调整拼接次数。由于基底和反射镜是相对固定的，且反射镜的镜面始终是波节，因此，基底上的光栅线是固定的，也就是第二次原子光刻和第一次原子光刻的重叠部分，光栅线是完美重合的，如图7（b）所示。

两次拼接得到的光学像和P1～P7点的AFM图像如图7（c）所示，驻波场方向光栅的峰谷高度从左到右随位置的变化如图7（d）所示。重叠部分的AFM图像表明，第一次沉积和第二次沉积的光栅线是完全重合的，光栅重叠部分的峰谷高度最高也说明了这一点。两次拼接原子光刻实验将光栅的驻波场方向长度拓展到4.8 mm，可根据需要调整拼接次数从而得到自溯源光栅尺长度。

3.3.3 大面积自溯源光栅制备的误差分析

对比单次自溯源光刻，除节距误差外[32］，大面积自溯源光栅的制备过程还会引入以下误差[44］：

（1）反射镜表面非平行性的误差；

（2）道威棱镜的插入会导致形成驻波场入射激光和反射激光不完全重合的误差；

（3）道威棱镜的引入和拼接距离的增加引起高斯激光相移误差。

3种额外误差见表3。单次自溯源光栅在22℃节距的理论最佳值为（212.770 5±0.004 9）nm，即使加上大面积自溯源光栅的额外误差（4.5×10-4nm），使用拼接原子光刻和扫描原子光刻技术制备大面积自溯源光栅的方法在保证光栅的均匀性和一致性的条件下，仍可以保证自溯源光栅极高的准确性。

表3 大面积自溯源光栅的制备过程中引起的额外误 差[44］Tab.3 Additional errors caused during preparation of large-area self-traceable gratings

3.4 二维铬光栅实验制备

利用二维驻波场和分步沉积技术可以获得二维原子光刻光栅，由于高斯光束相移[46］，二维驻波场的一致性会因为会聚激光的束腰离镜面位置的不同而变化。为了保证二维原子光刻光栅在两个方向的均匀性和一致性，并简化实验流程，本课题组提出了分步沉积制备二维自溯源光栅的方法[34，47］。分步沉积是用一维驻波场进行两次沉积，相对于二维驻波场的方法，实验操作简单且能保证两次沉积节距完全相同，因此成为我们制备二维原子光刻光栅的主流方法。

3.4.1 分步沉积制备二维铬光栅

3.4.1.1 实验原理

分步沉积制备二维铬原子光刻光栅是基于原子光刻技术，在一次原子光刻的基础上，旋转基板一定的角度之后再进行二次原子光刻，其基本原理如图8所示。

图8 分步沉积原子光刻示意图[34］Fig.8 Schematic diagram of two-step deposition of atom lithography

3.4.1.2 二维铬原子光刻光栅的自溯源特性

分步沉积制备铬原子光刻光栅的实验结果如图9（a）所示。由于两次原子光刻形成的光栅节距相等，因此二维原子光刻光栅相邻4个点形成的四边形是菱形结构，如图9（b）所示。由于菱形的对角线是天然垂直的，因此，分步沉积制备的二维原子光刻光栅对角线夹角具有溯源性，能直接溯源到标准图形的天然正交特征。

图9 （a）分步沉积制备的原子光刻光栅AFM图；（b）二维原子光刻光栅形成的菱形结构[34］Fig.9（a）AFM image of atom lithography grating prepared by two-step deposition；（b）Diamondshaped structure formed by two-dimensional atom lithography grating

3.4.1.3 二维铬自溯源光栅的准确性

分步沉积制备的二维铬自溯源光栅的自溯源角度溯源于一维铬自溯源光栅的长度。其中，一维铬自溯源光栅的理论最佳值为（212.077 05±0.004 9）nm（22℃），因此二维铬自溯源光栅的对角线夹角的理论最佳值为（90±0.002 7）°[34］（22℃）。为验证二维铬自溯源光栅的准确性，随机挑选了两个二维铬自溯源光栅到世界权威计量院PTB的测量结果，见表4。样品1的对角线夹角测量结果为（90.001±0.003）°（k=2），样品2的对角线夹角测量结果为（90.000±0.003）°（k=2）。与理论最佳值（90±0.002 7）°高度符合，且两样品的对角线夹角之差仅为0.001°。而二维光栅国际对比NANO5[48］，节距为300 nm二维光栅的非正交误差为0.5°。因此，使用自溯源光栅研制纳米尺度下的角度标准，对于确保角度的准确性来讲具有重要的意义。

表4 随机样品1和样品2的PTB测量结果Tab.4 PTB measurements for random samples 1 and 2 （°）

4 自溯源特性的传递和空间倍频

4.1 原子光刻技术结合软X射线干涉光刻技术

为进一步发展原子光刻自溯源光栅的优势，提出原子光刻结合软X射线干涉光刻制备自溯源光栅标准物质的技术方案。该方案不仅能精确缩短自溯源光栅的节距并扩展维度，而且融合了软X射线干涉光刻技术的特点，可以实现自溯源标准物质的大批量制造和光栅材质转移。

4.1.1 实验原理

图10为软X射线干涉光刻示意图。入射光经过衍射光栅后形成±m级的衍射光，掩模版后面某一位置处，-m和+m衍射光相交形成干涉条纹，衍射角θ为：

图10 软X射线干涉光刻示意图[49］Fig.10 Schematic diagram of soft X-ray interference lithography

其中：m为衍射级次，P0表示衍射光栅周期。两束衍射光干涉形成的条纹周期P1为：

其中θ为两束衍射光的夹角，满足几何关系。由式（3）和式（4）可得：

由式（5）可知，对于衍射光栅分束型装置，其曝光图案的周期仅和衍射光栅的周期以及衍射级次有关，与使用光源波长无关。

4.1.2 干涉光刻衍射效率分析

光栅衍射效率越高，干涉条纹对比度就越高，对曝光过程抗杂散光和背景光的干扰能力越强。因此，根据严格耦合波分析(RCWA）理论[50］，利用MATLAB程序计算透射光的衍射效率。综合考虑本底层和光栅高度，优化铬光栅的衍射效率。对于理想光栅，即无本底层情况下，本底层和光栅高度比值R=0，一级衍射效率在光栅高度为80 nm时最大，为9.4%，二级衍射效率在光栅高度为144 nm时最大，为3.0%；对于真实光栅（R=1），一级衍射效率在光栅高度35 nm时最大，为1.4%，二级衍射效率在光栅高度66 nm时最大，为0.09%[51］，如图11所示。

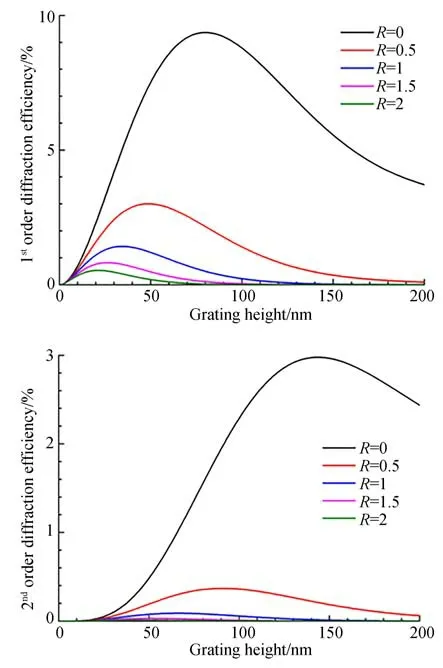
图11 光栅高度及光栅结构比值R对衍射效率的影响[51］Fig.11 Influence of grating height and grating structure ratio R on diffraction efficiency

4.2 一维干涉光刻和二维干涉光刻

使用原子光刻技术制备软X射线干涉光刻掩模版，须考虑两种技术的兼容性。采取掩膜光栅制备和基板开窗处理分离的方案。第一步，设计掩模版基板并对基板进行开窗处理；第二步，通过原子光刻技术在设计的基板上制备铬光栅。掩模版基板由100 nm的氮化硅膜层和0.29 mm的硅衬底组成。开窗处理采用湿法刻蚀，将硅衬底材料的一部分区域完全刻蚀至氮化硅膜层，只留下氮化硅膜层，氮化硅膜层区域称为“窗口”。X射线在窗口部分可以通过，挡光区域由于硅衬底的遮挡完全不能通过。

光栅掩模版的质量是决定曝光图形好坏的重要因素，不仅要考虑条纹结构质量，如线边缘粗糙度、均匀性等，还要考虑衍射效率和背景光的影响。考虑到其他衍射级次的光会影响曝光区域，一级干涉基板需要满足D≥L，二级干涉基板需要满足D≥3L。如图12所示，红色、蓝色和绿色分别表示一级、二级和三级衍射光（彩图见期刊电子版）。掩模版示意图如图13所示。

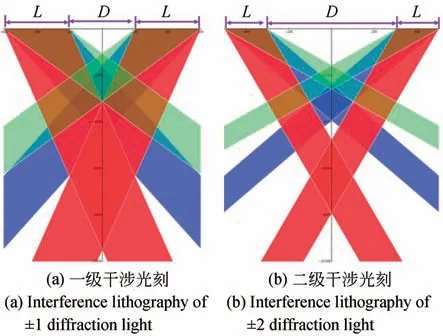
图12 掩膜版基板尺寸设计Fig.12 Size design of mask substrate

图13 掩模版示意图Fig.13 Schematic diagram of mask

4.2.1 基于一级衍射光干涉光刻

硅光栅样品的制备要经过清洗基板、涂胶、前烘、曝光、显影、后烘、刻蚀等阶段。样品准备流程主要包括：

（1）清洗基板表面：为清除表面可能的有机物，使用丙酮清洁基板表面，通过高速旋转的方式，转速为4 000 r/min，清洗1 min；

（2）旋转涂胶：将光刻胶缓慢滴在中心处，然后扩散至整个边缘，匀速转动使光刻胶在基板表面形成均匀的薄膜。转速为4 000 r/min，旋转时间为60 s；

（3）烘烤基板：旋涂完毕后，为去除残余溶剂和膜层，对基板进行烘烤，温度为180℃，共90 s。

将铬光栅掩膜和准备好的光刻胶样品放入曝光腔中，整个曝光过程需要在高真空环境下完成。涂有PMMA的样品曝光结束后，使用MIBK∶IPA=1∶3的显影液显影45 s后，用95%的无水乙醇清洗30 s，然后用氮气缓慢吹干样品表面。在使用ICP刻蚀前，样品在90℃烘烤30 s，除去残存的水渍。

硅的刻蚀通常依靠含氟气体与硅反应[52］生成挥发性物质，选择SF6和C4F8为反应气体对曝光样品进行刻蚀。PMMA属于有机物，主要由C和H两种元素构成，C和H的化学键相对较弱，物理轰击有一定的刻蚀作用，通入O2会生成挥发性的CO2气体和H2O提高刻蚀速率。利用一级衍射光进行干涉光刻可以得到节距为106.4 nm的硅光栅标准物质[53］，如图14所示。

图14 一维106.4 nm光栅的AFM图像Fig.14 AFM image of one dimensional 106.4 nm grating

4.2.2 基于二级衍射光干涉光刻

根据衍射效率的研究，高度约为50 nm掩模板已成功制备，接近理论的最佳值，使用二级干涉光刻的掩膜版基板，L=0.15 mm，D=0.45 mm，减弱了0级、1级、3级衍射光对干涉条纹的影响，提高干涉条纹的对比度。使用PMMA光刻胶在经过820 s的曝光时间后，经显影、后烘以及刻蚀后，成功制备了节距为53.2 nm的硅光栅，如图15所示。

图15 一维53.2 nm光栅Fig.15 One dimensional 53.2 nm grating

4.3 一维硅光栅的准确性

4.3.1 PTB测量结果

经权威计量机构德国PTB测量验证，随机两个106.4 nm硅光栅的节距分别为（106.449 6±0.004 9）nm（k=2），（106.450 7±0.006 3）nm（k=2），不确定度小于0.01 nm。表5展示了PTB的测量结果。

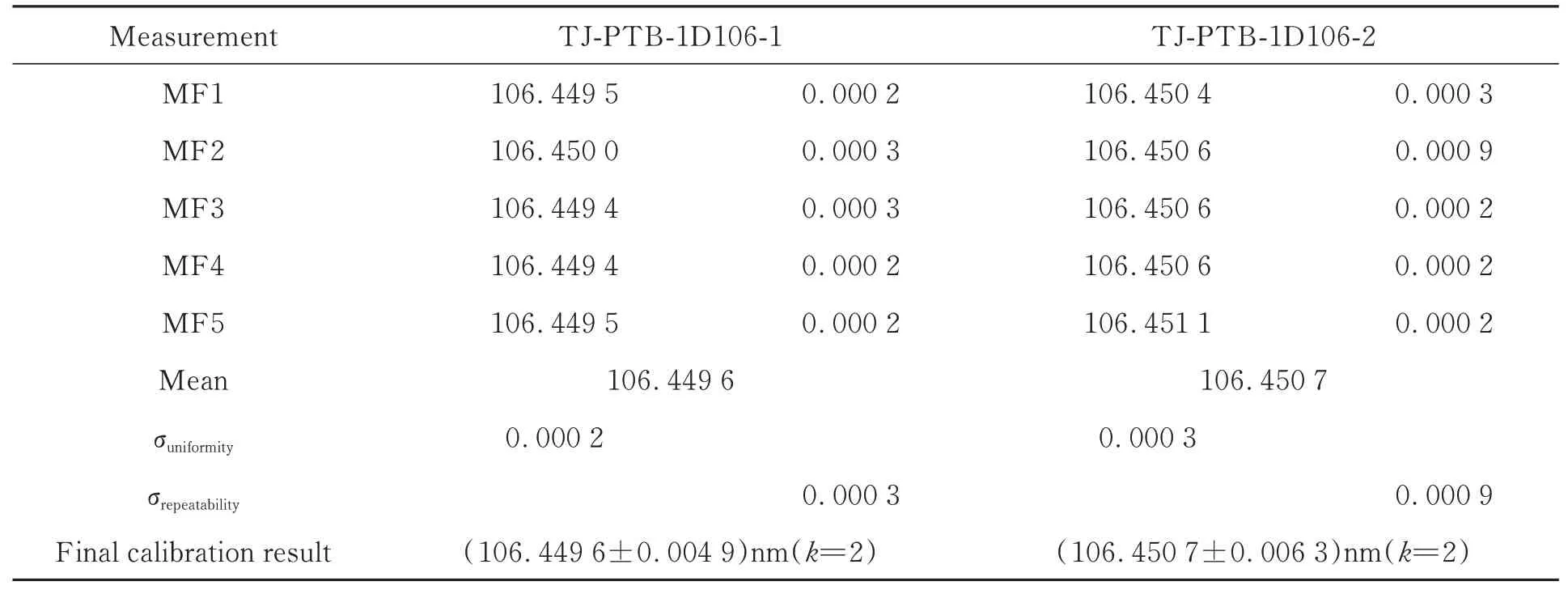
表5 一维106.4 nm硅光栅PTB的测量结果Tab.5 Measurement results of one-dimensional 106.4 nm silicon grating by PTB

4.3.2 国家一级标准物质

经过长达一年的均匀性检验与稳定性检验，一维106.4 nm硅光栅目前已成功申报为国家一级标准物质，图16为国家市场监督管理总局颁发的标准物质证书。

图16 一维106.4 nm硅光栅国家标准物质定级证书Fig.16 Gradation certificate of national certified reference material of one-dimensional 106.4 nm silicon grating

4.3.3 校准SEM

SEM的放大倍数和非线性校正是一项重要的工作。利用原子光刻技术和X射线干涉光刻技术结合制备得到的一维106.4 nm硅光栅，可以作为扫描电子显微镜的横向校准标准[13］。

为了校准其性能，样品由德国联邦科学技术研究院开发的计量型大范围原子力显微镜（Met.LR-AFM）测量。标定后的光栅平均节距为106.457 nm，与理论值吻合较好。使用标定光栅校准商业扫描电镜，放大50kX获得的典型扫描电镜图像如图17（a）所示。在计算如图17（b）所示的图像剖面的平均强度之后，使用阈值法确定每个结构的中心位置。图17（c）是数据拟合后的位置偏差曲线，该位置偏差曲线反映了扫描电镜的场畸变。如图17（d）所示，在SEM测量中这种场畸变表明像素大小在SEM图像中不均匀。由于扫描电镜在扫描场的前1/3处具有很强的非线性特性，因此在校准放大倍数时，只计算图17（c）中灰色框中标记的扫描区域的最后2/3。通过对图17（c）中最后2/3的数据进行线性拟合，利用仪器的实际放大倍数计算出该位置的扫描电镜测量的平均节距值107.177 6 nm。扫描电镜得到的节距值与计量工具得到的节距值之间存在偏差，所以有必要修正扫描电镜的标度。

通过比较从SEM得到的平均节距值PSEM和Met.LR-AFM得到的校准值PRef，扫描电镜测量的标度修正系数k可计算为：

参数k既可以应用于扫描电镜测量软件中，也可以应用于数据评估软件中进行修正。

图17（e）给出了从10个不同测量位置确定的k，误差条指示每个位置10次重复测量的标准偏差。由图可见，k的最大变化小于0.05%，证实了用这种新标准校准扫描电镜的优越性。

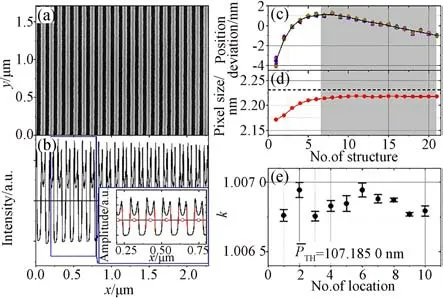
图17 （a）光栅样品的SEM图像；（b）光栅SEM图像剖面的平均强度分布；（c）扫描电镜场畸变的位置偏差曲线；（d）沿快速扫描方向SEM的校准像素，虚线表示SEM给出的标称像素；（e）在光栅的10个不同随机位置校准的SEM的比例因子k[13］Fig.17（a）SEM image with of grating sample；（b）Averaged profile of the SEM image along the y direction；（c）Position deviation curve indicating the scanner distortion of the SEM；（d）Calibrated pixel size of the SEM along the fast scan direction（x）；The dashed line indicates the nominal pixel size given by SEM；（e）Scaling factor，k=PSEM/PRef，of SEM calibrated at 10 different randomly selected locations of gratings

由于自溯源光栅图形同时具有大范围和小范围的均匀性，只要随机选择一个或几个测量位置，就可以很好地标定扫描电镜。常规校准过程中两个重要问题得以解决，即重新定位预先定义的测量位置所需的巨大努力；以及避免由于重复扫描电镜测量的污染问题而导致的特征图样损坏。

5 基于硅晶格常数的线宽量值测量

5.1 引入硅晶格常数的意义

单晶硅的晶格间距是许多重要物理常数测量的基础。硅的d220晶格间距已被广泛测量，其值为192.015 571 4×10-12m[54］，标准不确定性为0.000 003 2×10-12m。在纳米尺度，硅晶格间距被国际计量局（BIPM）批准成为新的纳米尺度下“米”定义的补充复现形式[55］。随着2019年国际单位制的修订，对米的实践方法的一个重要补充是引入了基于硅晶格参数的米。在长度测量中引入硅晶格常数便于建立测量的溯源体系，也有利于推动纳米几何量测量的溯源体系的研究。

5.2 标准线宽样品的制备

5.2.1 线宽的定义

线宽是指线条两侧平均线边缘之间的距离[56］。

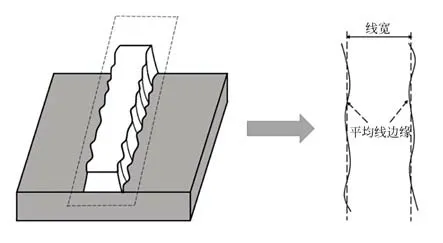
图18 线宽示意图Fig.18 Line width diagram

5.2.2 制备流程

标准线宽样品的制备采用多层膜沉积技术，将沉积膜层的厚度值转化为线条结构的名义线宽值，该方法可以保证样品线宽量值的一致性和样品整体的稳定性。针对多层膜材料，以Si/SiO2为基础，将线宽引入硅晶格常数便于建立测量的溯源体系，采用磁控溅射方法，根据沉积速率制备不同的多层膜结构。制备流程如图19所示，将两块样品进行键合、切割和研磨抛光处理，并选择湿性刻蚀方法制备与半导体工艺相兼容的多层膜线宽结构。

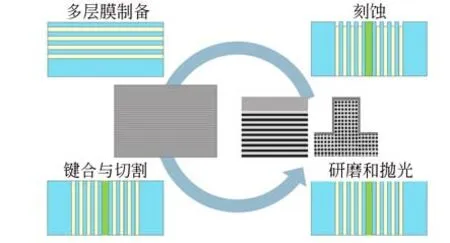
图19 多层膜线宽制备流程Fig.19 Multilayer film line width preparation process

5.2.3 制备结果

制备后的线宽样品如图20～图22所示。2021年，同济大学制备的多结构硅纳米线宽由国家市场监督管理总局发文批准成为国家二级标 准 物 质。具体线宽为（44.9±3.8）nm（k=2）；（84.2±5.1）nm（k=2），三是线宽为（165.4±8.9）nm（k=2），如 图23所示，其 标 号 为GBW（E）130744。上述标准物质增加了我国有证线宽标准物质的种类，为实现我国在纳米长度计量方面的多尺寸测量提供了标准物质。

图20 硅片切割效果图Fig.20 Image of cut silicon wafer

图21 热压键合样品的AFM图像Fig.21 AFM image of thermocompression bonded sample

图22 Si/SiO2多层膜光栅样品Fig.22 Si/SiO2 multilayer grating sample

图23 多结构硅纳米线宽国家标准物质定级证书Fig.23 National standard substance classification certificate for multi-structured silicon nanowire width

5.3 基于硅晶格常数对线宽的测量表征

研制高精度的关键尺寸标准物质是纳米计量学的一项重要任务，晶体晶格校准是一种很好的校准线宽样品的方法，可以作为一种新方法来实现纳米尺度线宽量值计量的自溯源性测量[57］。

根据精确的X射线测量，未掺杂的Si（111）的间距为313.560 11（17）pm[57］，由于单晶硅的晶胞排布方式为立方金刚石型，故使用Si（111）作为测量标准在溯源性上和国际上常用的Si（220）基本等同，如图24所示。在硅晶格关键尺寸的测量与校准中，我们将非晶态线宽结构与晶体硅线宽结构一同扫描，使之在同一帧图像中被检测到，如图25与图26所示。

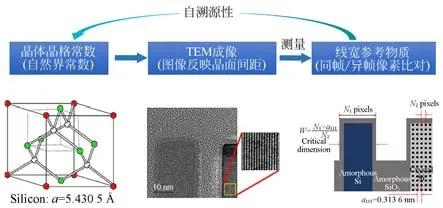
图24 非晶硅线宽校标的自溯源性测量Fig.24 Self-traceability of amorphous silicon linewidth calibration

图25 非晶硅线宽校准示意图Fig.25 Calibration diagram of amorphous silicon line width

在TEM的扫描图样下可以清晰地看到样品内硅晶面间距的排布，待测线宽样品的像素值为N1，单一硅晶格间距的像素值为N2，则样品的实际测量值为。即完成非晶硅线宽尺寸的可溯源性测量与校准。

如图26所示，利用右侧Si（111）衬底的硅晶格常数以及在同一帧图像上像素点的比值，能够较为精确地对标准线宽临界尺寸进行定值。

图26 多层结构线宽不同部分的TEM图像Fig.26 TEM images of different part of multilayer structures

我们计算临界维度的像素数N1，首先得到两个相邻的Si（111）平面之间的像素数。沿Y轴的指定线的CD值由计算，其中a111相当于0.313 6 nm的 常 数。图27中，Y=400，500，600，700和800处 的CD值 分 别 为20.9，21.0，21.2，20.8和21.3 nm，得出平均CD为（21.0±0.2）nm。该结果与已有的研究很一致，即均匀性可以控制在0.3 nm以下。因此，以硅晶格常数来对非晶硅进行自溯源测量定值的方法是可行的。

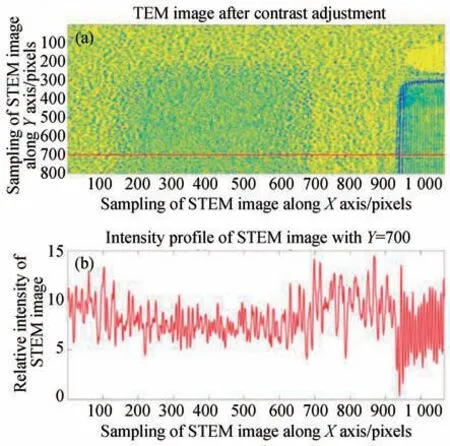
图27 （a）对比度调整后CD的TEM图像再现；（b）TEM图像沿（a）中Y轴的指定线的图像强度曲线Fig.27（a）Reproduction of TEM image of CD after contrast adjustment；（b）Image intensity profile of TEM image at specified line along Y axis in（a）

5.4 探针校准器

在AFM对线宽样品进行扫描时，由于扫描针尖的膨胀效应，对纳米结构的测量值往往会大于实际值，所以需要对AFM探针进行定值与校准。由于前文中的线宽量值可以用硅晶格常数精确地标定，同时线宽也近似一个矩形，因此该线宽标准物质非常适合作为一个标准的探针校准器对AFM探针进行校准，如图28所示。基于Si/SiO2多层膜光栅技术的探针校准器主要包含两个部分，第一部分是5～20 nm的线宽结构，用于提取探针的轮廓信息；第二部分是10～50 nm的凹槽结构，用于提取探针的深宽比信息。综合两个部分，对探针进行反复测量可以得到较为精确的探针表面信息。测量结果表明，校准器样品整体比较均匀，线宽测量值与名义值较为接近。对多层膜探针校准器线宽部分和凹槽部分的关键参数进行详细表征及等效性测量，能够有效地评估样品间的均匀性，同时也能够找出目前结构的不足之处并进一步优化。这一研究有助于多层膜探针校准器的广泛应用。

图28 多层膜探针校准器的膜层设计和线宽区域AFM图像Fig.28 Film layer design and linewidth area AFM images of multilayer film probe calibrator

6 结 论

研制一维节距、二维栅格、线宽等纳米计量标准物质是实现纳米尺度长度溯源性传递，保证几何量值测试的统一性和准确性的关键环节。本文总结了原子光刻技术及原子光刻与软X射线干涉技术相结合的原理及关键实验流程，制备了节距为212.8 nm和106.4 nm的一维自溯源光栅，并获批国家一级标准物质。后续基于自溯源光栅的AFM、SEM等精密计量仪器的校准研究，也充分证明了自溯源光栅是作为一维纳米节距标准的理想物质。扫描原子光刻技术和拼接原子光刻技术的研究，实现了自溯源光栅的尺寸从微米量级向毫米至厘米量级尺度的拓展，进一步为自溯源标准物质在位移测量、加工校准等后续的应用奠定了基础。在纳米角度计量领域，基于分步原子光刻沉积方法制备的二维自溯源标准物质也展示出角度天然正交的特点，这为纳米尺度下精密仪器的角度校准和正交性判断提供了新的思路。另一方面，通过多层膜沉积技术研制的多结构硅纳米线宽标准物质进一步增加了我国线宽标准物质的种类。线宽校准器等相关研制工作的开展，也为后续探针重建及精密测量仪器的修正等应用提供了重要的标准样品。