全息光栅实验的教学研究
2022-07-27赵康鑫郎赤诚陶冠奇康秀英彭宇帆王引书
赵康鑫,于 昊,郎赤诚,陶冠奇,康秀英,彭宇帆,王引书,,d
(北京师范大学 a.未来教育学院,广东 珠海 519087;b.实验与实践创新教育中心,广东 珠海 519087;c.物理学系,北京 100875;d.文理学院,广东 珠海 519087)
任何具有空间周期性的衍射屏都可以称为衍射光栅,光栅是极为重要的分光元件[1],广泛用于单色仪、摄谱仪、光谱仪、光纤通讯、光计算机技术、光信息处理系统等领域[2]. 全息光栅的制作原理是相干光干涉条纹在全息干板上的记录,制备方法有菲涅耳双棱镜法、阿贝成像原理法、杨氏双缝干涉法、菲涅耳双面镜法、迈克耳孙干涉法、马赫-曾德尔干涉法等[3-6]. 全息光栅的制作与表征涉及光的干涉、衍射原理,通过全息光栅的制作与表征,可以将全息技术、夫琅禾费衍射原理与技术、光谱仪及分光计的应用等实验内容有机结合,学生可以学习如何应用相关知识,从不同角度,用不同分析技术综合研究特定问题,建立严谨对待实验结果的科学态度;同时以光栅技术为切入点,可以了解与之相关的光刻等高端技术. 因此,全息光栅的制作与其参量测量在大学物理实验教学中占据重要地位,对培养学生自主探索、综合应用相关知识等有一定意义.
本文利用不同光路的激光全息方法制作了多组光栅常量各不相同的一维、二维全息光栅,用不同的方法测量了所制作光栅的光栅常量和衍射强度分布,结合Matlab软件模拟分析了影响正弦型光栅衍射强度分布的因素,给出了制备全息光栅参量可控的实验条件,探索了将多个光学实验进行有机结合,培养学生从不同角度研究同一物理问题的思维方法,提高学生综合分析问题和解决问题的能力.
1 实验仪器与方法
在光学平台上完成全息光栅的制作,采用655 nm的半导体激光器作为光源,分别采用了如图1所示的三角形光路和马赫-曾德尔干涉光路来制作一维全息光栅,二维全息光栅的制作是在一维光栅的基础上,通过将全息干板旋转90°进行二次曝光制作完成. 制作光栅的条件如表1所示. 实验首先用光纤光谱仪测量激光器的光谱来校准激光的波长;然后用光学显微镜观察光栅的结构,并用分光计准确测量光栅的衍射角;最后用夫琅禾费衍射实验仪测量光栅衍射的强度分布,计算光栅常量并进行对比分析. 采用Matlab软件模拟正弦型光栅的衍射强度分布,综合分析全息光栅的衍射特性.

(a)三角形光路 (b)马赫-曾德尔干涉光路图1 实验光路

表1 光栅制作的设计参量及测量的光栅常量
2 实验原理
2.1 全息光栅制作原理
图1中的三角形光路和马赫-曾德尔干涉光路的工作原理相同. 下面以三角形光路图为例来说明工作原理. 图1(a)中激光经过扩束镜与准直镜后,得到1束平行光,平行光经分束镜分束后,得到2束相干光,经反射镜反射后,2束相干光在感光板处发生干涉.
图2所示为三角形光路图中经过反射镜后的光路简化图. 图中M1和M2反射出的2束相干光的波矢为k1和k2,两波矢与接收面法线(z方向)的夹角分别为θ1和θ2.2束相干光之间的夹角为φ=θ1+θ2,入射光波长为λ,则光栅常量为[4]
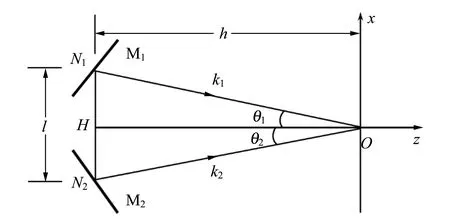
图2 三角形干涉光路简化图
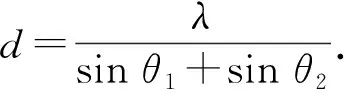
(1)
当θ1=θ2=θ时,
2dsinθ=λ,
(2)
式(2)即为制作全息光栅时的光栅方程.实验上通过测量图2中光栅制作时的干涉角可以得到设计光栅的光栅常量.
2.2 全息光栅的衍射原理
激光照射平面衍射光栅时,会发生夫琅禾费衍射.如图3所示,在光屏P1和P2处分别出现±1级的衍射光斑,更高级次的衍射光斑距离光屏中心更远.

图3 光栅衍射示意图
平面衍射光栅方程为[1]
dsinθj=jλ,j=0,±1,±2,…
(3)
其中,θj为衍射角,d为光栅常量,l±1为±1级亮条纹至0级光斑的距离.根据衍射光路的几何关系,即可在实验上测量光栅常量d.
3 实验结果与分析
3.1 全息光栅的结构


(a)一维(100×) (b)二维(100×)图4 显微镜观察光栅表面图像
3.2 衍射光斑的几何关系及光栅常量测量
图5为光栅A的一维、二维全息光栅衍射图. 实验中只观察到0级、±1级衍射斑点. 夫琅禾费衍射图频谱的亮点数量反映了光栅的类型. 如果夫琅禾费衍射图的频谱只有0级和±1级,则表明此光栅是正弦型光栅;如果其频谱出现2级、3级…亮点,则表明此光栅是非正弦型光栅;当亮点很多时,表明该光栅接近矩形光栅[7-8]. 本文采用激光全息法制得的全息光栅频谱只有0级和±1级,表明所制备的光栅是标准的正弦型透射光栅. 可以使用光栅方程式(3)计算其光栅常量. 为保证实验结果的精确,用光纤光谱仪测量了实验中所使用的半导体激光器的光谱,如图6所示,中心波长为λ=655.77 nm.

(a)一维 (b)二维图5 光栅A的夫琅禾费衍射图样

图6 激光器的光谱图

显然,三角形干涉光路的误差大于马赫-曾德尔干涉光路. 但是三角形干涉光路搭建简便,干涉现象直观,更有利于学生理解实验原理,且制得的光栅正弦性好,因此在课时少的实验中推荐使用三角形光路干涉法.
3.3 用分光计测量全息光栅的衍射角和光栅常量
用衍射光路几何关系测量光栅常量,一般存在较大误差. 采用分光计能够精确测量出衍射角θj以计算光栅常量. 表2为分光计测量的光栅A和B的0级与±1级衍射角对应的刻度盘读数. 目镜由-1级转至+1级时所转过的角度为
(4)


表2 分光计测量光栅衍射角的数据
显然,三角形干涉光路所得光栅常量的相对偏差小于马赫-曾德尔干涉光路,且通过解三角形的方法预测出的光栅常量较测量衍射角计算光栅常量有更大的偏差. 分光计测量光栅常量的可信度更高,是精确测量光栅常量的方法,本文将分光计测定的光栅常量作为此实验的理论值. 但是,分光计法的缺点是载物台与目镜距离的限制,在衍射角较小,即光栅常量较大时,使用分光计测量衍射角可能会使0级条纹与±1级条纹重合,导致测量结果不准确.
比较显微镜图像和分光计方法的结果,显微镜图像的测量值相对于分光计法测量值的相对偏差为:δA=0.4%,δB=1.3%.显然相对偏差较小,测量的光栅常量准确度较高.当衍射角较小,即光栅常量较大时,显微镜法则是更好的测量光栅常量的方法.
3.4 全息光栅衍射强度的分布
全息光栅是平面衍射光栅的一种,其衍射光强的分布可一定程度上反映光栅的质量. 用夫琅禾费衍射仪测量了全息光栅A和B的衍射强度的分布. 光栅B的衍射强度分布如图7所示. 从图7中可以看出,±1级的衍射强度远远小于0级的衍射强度,所制作的其他光栅的衍射强度的分布与之类似. 由双光束干涉原理知,2束振幅相同的相干光发生干涉时,在干涉位置的光强分布可以写为
(5)


图7 全息光栅B衍射光强随位置x的分布图
由衍射透过率函数可知正弦型光栅的夫琅禾费衍射在x方向上的光强分布为[8]
(6)
其中,L为有效光栅边长,表征激光通过有效光栅面积的大小;z为光栅至接收屏的距离;m≤1,表示透过率函数呈正弦变化的幅度.则中央主极大位置的光强为
(7)
可得0级和±1级3个亮点的相对光强为1和m2/4,在全息光栅的频谱中只能观察到这3个亮点,表明此光栅正弦型良好.对于光栅A和B,在衍射距离z=11.50 cm时,±1级相对光强约为0.33%和0.78%,则mA=0.19,mB=0.10.用Matlab模拟做出正弦型振幅光栅夫琅禾费衍射强度的理论分布如图8所示,正弦型振幅光栅的夫琅禾费衍射频谱半角宽度由有效光栅大小L决定,相对强度由m决定.从图8中可以看出,随着L逐渐变小,衍射频谱展宽,但相对位置和幅值不变,展宽是由于光栅尺寸变小产生的.由图9可知m会大幅影响衍射相对强度,这也是图7中把±1级位置放大50倍才能看到的原因.

图8 正弦型振幅光栅衍射强度的理论分布(m=1)

图9 正弦型振幅光栅衍射强度的理论分布 (L=0.05 mm)
在制作全息光栅时,可以通过控制光路得到正弦性非常好的全息光栅,但对于此光栅的衍射光强和斑点特征,并不由光路决定,而是由m和L同时影响[8],最终导致全息光栅衍射0级与±1级光强之比较大.同时,光源距离接收屏越远,接收到的光强就越小,即使示波器积分区间调整至最大,观察到的波峰变化也会非常小.故实验中需将整体光路距离适当减小,使衍射强度分布更加明显.

(8)
由测量的衍射谱中±1级的峰位,计算出光栅A和B的光栅常量dA=8.02 μm,dB=6.56 μm,与分光计法测量值的相对偏差为δA=1.5%,δB=1.0%,相对偏差较小.
3.5 全息光栅的可控制作方法分析
从理论上讲,只要在制备操作中做到足够精确,就能得到预期光栅常量的全息光栅,但从图10光栅常量随干涉角、衍射角的变化图中可以看出,在干涉角度较小(d>10 μm,φ=1.88°<0.033 rad)时,曲线斜率的绝对值会非常大,对干涉角度控制的精确度要求会迅速提高,故在小角度干涉时对光栅规格的控制会变得十分困难.同理,衍射角较小(θj=3.76°<0.066 rad)时,通过观察频谱来确定光栅常量会有更大误差.
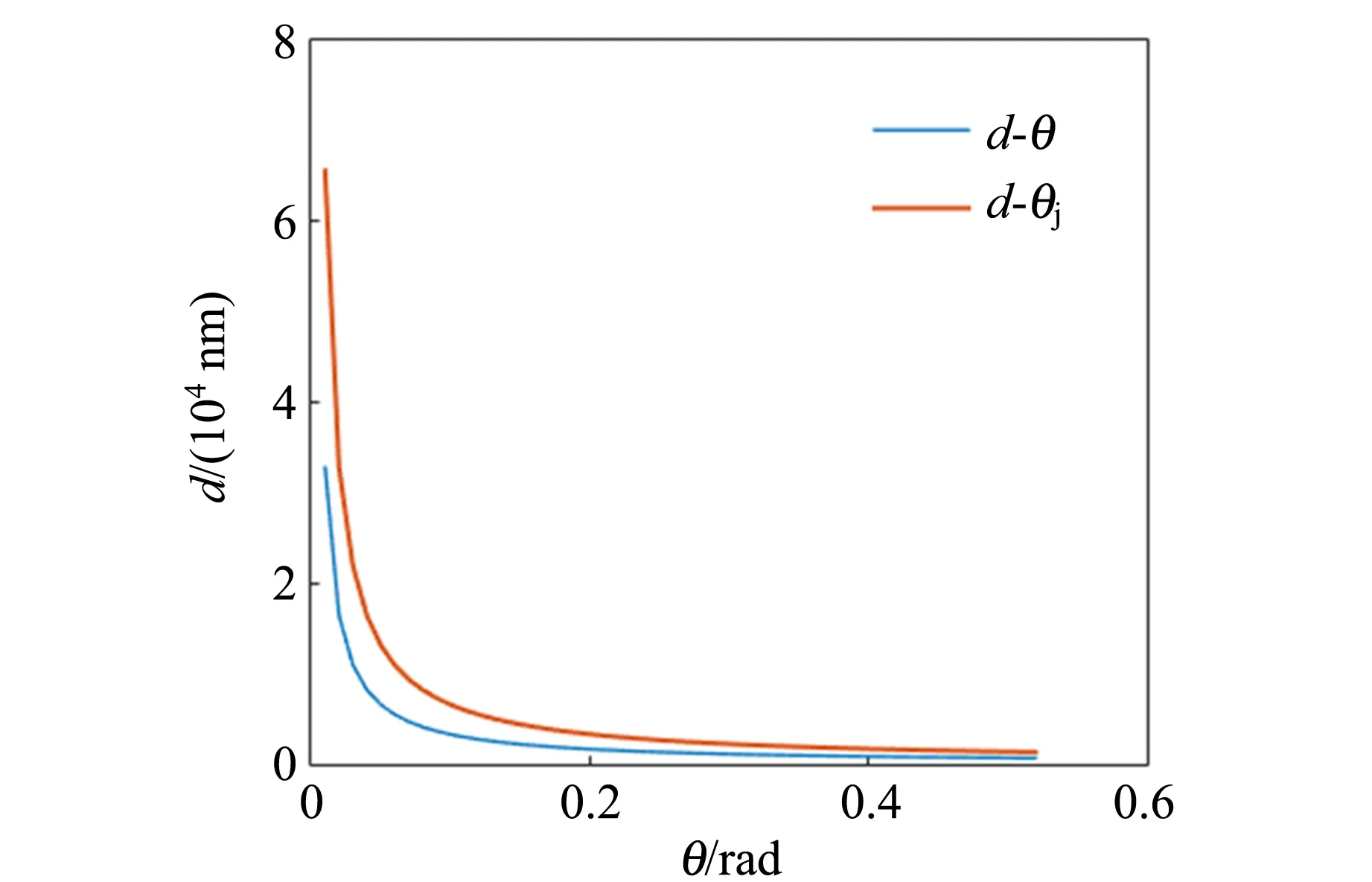
图10 光栅常量随干涉角和衍射角的变化曲线
d=ky.
(9)
图11所示为d随y的变化关系,可以得出λ=687.86 nm,与光谱仪测量的激光波长655.77 nm的相对偏差δλ=4.9%,R2=0.999 3.显然,通过控制干涉角来测量光栅常量的误差很大,由图11中最后1个实验点可以看出,当干涉角过小,即值过大时,预测值误差则会更大.在干涉角φ>3.76°时,通过控制φ来控制光栅常量的大小是可行的.制作较大光栅常量的光栅时,使用马赫-曾德尔干涉光路更方便,由于其良好的“平行四边形”特性,可以使得双光束干涉角度较小.三角形干涉光路无法满足此时足够小的角度,这也是马赫-曾德尔光路的优势所在.

图11 通过干涉角预测光栅常量的实验点拟合
在一次测量的情况下,不涉及重复测量,不考虑A类不确定度,则ul=uh=uB=0.29 mm,uA=0,则光栅常量的不确定度ud=2×10-8m;即对于光栅A,其理论预测光栅常量值d=(8.20±0.02) μm. 由以上分析可知,仪器精度对预测光栅常量的影响较小,可采用多次测量的方法降低人为测量误差.
4 结束语
通过光栅制备及表征实验,将全息技术、分光计应用、光谱仪技术及应用和夫琅禾费衍射等实验有机结合成光学模块体系,不仅可以使学生对光学知识有更深入地理解,还能够让学生深入体会自主探究性学习的思路和方法,提高学生创新思维和科学素养.
