“双碳”背景下核电收益权资产证券化定价研究

马智胜， 孟寒雪

(东华理工大学 经济与管理学院，江西 南昌 330013)

核电作为目前唯一能够大规模替代化石能源基荷电源的绿色能源，是保障我国新型电力系统持续稳定供电的重要清洁能源之一，也是“双碳”目标下我国实现能源绿色转型的重要选项[1]。相较于水力、风能、光伏等能源，核电能量密度高、换料周期长、单机功率大且运行稳定，可以有效弥补上述可再生能源因具有随机性、波动性、周期性而无法满足常年高比例消纳需求的不足。同时，核电具备突出的低碳甚至“零碳”属性，全寿期碳排放水平是光伏发电的五分之一，整体比煤电低两个数量级[2]。因此，在我国实施“双碳”目标战略、构建低碳化能源体系的总体要求下，核能在我国未来能源体系中的比重将稳步提升，我国核电建设规模与速度也将有所上升。

核电建设需要长期、巨额的资金前期投入，行业杠杆率居高不下，建设资金缺口压力严峻。国家发改委和国家能源局发布《“十四五”现代能源体系规划》(发改能源〔2022〕210号)指出：计划2025年实现核电运行装机容量达7 000万千瓦，在建达到3 000万千瓦以上,争取2030年实现核电占比8%[3]。根据发展规划与项目核准情况，以三代核电总投资200亿元/台(2亿元/万千瓦)估算[2]，实现规划装机容量所需资金达5 000亿元，按每年新增6～8台核电机组计算，年总投资额为1 200～1 600亿元，加上研发及环保设施建设成本，年总资金需求将超2 000亿元。有专家预测，鉴于减排压力及能源低碳转型，我国核电项目核准速度将会加快。

如何创新融资渠道与方法，利用“高能资金”[4]破解核电建设资金缺口和高杠杆率的双重约束？ 通过核电全寿期资金投入与收益分析，结合我国高速公路、水电、城建等大基建项目的融资实践，我们认为，通过资产证券化模式，将核电收益权资产转化为可在资本市场交易的金融商品进而获得低成本融资，是一种积极的尝试。核电售电收益现金流稳定且保障程度极高，是优质的证券化基础资产，关键是如何结合收益权资产及核电行业特点，推出证券化产品并对其客观合理定价，实现低成本融资。

我国资产证券化研究起步相对较晚，早期的应用也仅针对银行不良资产等，随后才逐渐扩大至企业债权、消费金融贷款等各类资产。近年来，针对资产证券化在能源领域的应用研究逐渐增多，Joshi从法律逻辑和信用评级角度分析了可持续性能源证券化融资问题[5]。Alafita等通过设计太阳能发电证券化运作模式及定价方法进一步拓展了证券化融资在清洁能源发电领域的应用[6]。澜沧江水力发电、黄河上下游电投资产证券化可行性也得到了论证。针对核电资产证券化，目前既无相关运营模式设计，也没有定量资产定价分析。由于核电资产的特殊性，事故危害性极大，在运营管理及产品定价方面需结合其固有特点进行专门研究。基于此，以核电收益权定价为切入点，寻求合适的核电收益权资产证券化的定价方法与产品设计思路，以期为我国核电融资实践创新提供参考。

1 资产证券化定价方法研究综述与选择

目前，学界对于证券化定价方法的研究可归纳为两大领域：基于价值评估的现金流折现法和函数模拟法。现金流折现法主要包括静态现金流折现法、静态利差法及期权调整利差法三种。静态现金流折现法假定贴现率在产品存续期内保持不变，对不同期间现金流使用单一固定利率折现。该方法计算简便，但对于精确定价适用性较差，目前大多用于定性分析。田庆锋等通过构建核电收益静态现金流折现模型，利用敏感性分析识别出影响核电资产证券化融资成本的主要影响因子[7]。静态利差法在此基础上考察利率期限结构，不同时点现金流对应不同贴现率，以市场各信用等级债券平均风险溢价作为固定利差。这在很大程度上改进了静态现金流法的缺陷，使得计算结果更贴近实际价值。闫妍和鲁皓均采用静态利差法对高速公路通行收入进行证券化定价，分别构建Nelson-Siegel和ARIMA-GARCH模型并结合实际算例验证方法的可行性[8,9]。针对港口资产，王思远利用GARCH-M模型量化权益类证券化产品风险溢价并论证了静态利差法的适用性[10]。静态利差法更适合偿付现金流固定，基本不存在提前偿付和主动违约的资产支持证券定价。期权调整利差法在静态利差法的基础上进一步确定证券化产品内嵌主动违约及提前偿付的期权价值，通过估算各利率变动路径下履行早偿和违约期权的概率，确定产品价格的期权固定利差后进行现金流贴现。McConnell于1981年首次提出期权定价概念[11]。Hürlimann假定利率固定，通过二叉树模型确定银行抵押贷款资产证券化期权价值[12]。目前，期权调整法主要运用于住房抵押贷款、融资租赁等存续期较长、偿付现金流对利率变化比较敏感且资产违约和早偿数据完备的基础资产定价[13-16]。函数模拟法的定价思路是基于已有资产价格函数，通过随机抽样模拟不同时点证券价格。该方法要求利率完全市场化，否则无法保证模拟效果。目前，函数模拟仅运用于现金流预测阶段。赵亮等以单因子Gaussian Copula模型对“第一期开元信贷资产证券化”产品进行现金流及利率模拟[17]。张勇假设信贷资产现金流服从布朗运动[18]，基于最优资本结构计算债券定价解析解。曹宏铎等构造了嵌入Gamma过程的Bass随机扩散模型模拟文化资产收益，并用大陆票房数据验证模型预测效果[19]。因此，函数模拟法更适用于完善金融体系下现金流具有强路径依赖的ABS产品。

通过对证券化定价方法及实践的梳理显示，静态利差法更加契合核电收益权资产全寿期长、现金流固定、利率敏感性低的特点，是目前最合适的定价方法。一方面，核电基础资产提前偿付和违约率等历史数据缺失，进行利率路径模拟和期权价值估计误差较大。虽然许多收费收益权产品发行项目书中均规定了发行人有权赎回一定比例资产支持证券，但该回购行为并不构成实质提前偿付期权，而是作为一种降低认购者投资风险的增信措施。另一方面，我国利率市场化程度不高，尚无成熟普适性资产价格函数，不具备函数模拟实践前提。此外，现阶段我国核电实行全额消纳政策，无补贴情况下项目ROE也在10%以上，收益现金流稳定[20]，资产违约风险与利率敏感性极低，因此进行核电收益权资产证券化定价时，应重点考量利率期限结构及各信用风险溢价影响。采用静态利差法对核电收益权资产证券化定价进行进一步探讨，结合蒙特卡洛模拟算法和NSS利率模型提出具体定价思路，以确定证券化产品融资规模及各信用等级产品理论价格和结构比例。

2 理论模型

基于静态利差法对核电收益权资产证券化进行定价及产品设计。假定以核电站某机组售电收入收益权为基础资产，发行期限为N年的ABN产品，按年付息，到期还本。总体定价步骤分为四步。

2.1 预测基础资产未来净现金流(NCFt)

核电站主要现金流入为售电收益，核电站实现商业运行并网后与电网公司达成一系列售电协议并以实际发电量结算发电收入。我国核电现阶段实行标杆电价机制，且核电尚未参与电量调峰，故核电站售电收益=发电量×核电标杆上网电价。核电机组实际发电量=机组额定容量×负荷因子×运行期限。在不考虑机组退役处置费用的情况下，运营期间现金流出主要包括资产折旧费、燃料费用、乏燃料处理费、机组运维费、财务费用及相关税费。该模型中假定核电站机组资产余值为0，折旧额采用年限平均法计算。根据财政部发布的《国家税务总局关于核电行业税收政策有关问题的通知》，核力发电企业享受增值税先征后退政策，故不考虑增值税影响，模型中仅考虑企业所得税。当核电站尚未进入运营期，其现金净流量为初始投资成本。将净现金流影响因素汇总为税后口径如下：

(1)

P为核电上网电价，θ为电价增长率，W0为核电装机额定容量，σt为核电机组负荷因子，Tyear为机组设计寿命，Cinv为初始投资成本，Cdis为乏燃料处理费用，Cope为运维成本，Cfin为财务费用，Cons为燃料消耗量，Uprice为铀价，ti为所得税税率。

2.2 拟合到期收益率曲线

依据闫妍分析国债利率期限结构得出改进后的Svensson模型拟合效果更佳的结论[8]，采用NSS模型进行期限结构分析。拟合数据选择方面，虽然现有研究多采用国债作为样本数据，但考虑到我国国债利息免征企业所得税，国债收益率实质隐含免税效应；而政策性金额债收益无相关税收优惠，其中占比九成的国开债信用评级与主权国家信用评级保持一致，契合市场基准地位要求。故使用国开行金融债数据拟合无风险收益率曲线。

Nelson Siegel Svensson模型表达式：

(2)

由即期利率为远期利率积分后求均值，则r(t)关于剩余期限t的函数为：

(3)

其中，β0、β1、β2、β3为待估参数，t为剩余年限，f(t)为远期利率函数。

目标函数为：

(4)

其中，CFij为第i支债券在第j期的现金流，rij为第i支债券在第j期的即期利率，tij为第i支债券在第j期距定价时点的时间差，NPi为第i支债券的净价，AIi为第i支债券的应计利息，ωi为第i支债券的权重。ωi= 1/Di，其中Di为债券的久期[5]。根据目标函数拟合结果得到待估参数值，将其带入公式(2)计算可得不同年限t债券到期收益率。

信用利差计算公式为：

(5)

其中，m为票面利率，N为到期日，P为债券市价，rt为债券第t期的即期收益率，Z表示债券信用利差Z-spread。

2.3 确定总体及各信用等级融资规模

资产池总体发债规模通过贴现现金流法进行计算，由(1)式可得基础资产的净现金流(NCFt)及到期收益率rt，故总体发债规模NAV为：

(6)

利用NSS模型拟合的对应等级债券到期收益率曲线，将步骤一中模拟的不同保障程度现金流数额根据公式(6)，利用贴现现金流法可计算确定各级债券发行规模。

2.4 确定各等级债券票面利率

假定除次级产品外，AAA及AA+证券化产品均为平价发行，发行价格与票面面值一致，为100元，年末付息，到期还本，发行期限与基础资产未来现金流期限一致，到期日为T，票面利率为R，票面利率确定公式为：

(7)

其中，N为产品期限期数，rt及rn为根据相同信用等级债券利率期限结构曲线确定的即期收益率。

3 实证分析

为检验上述数学模型及定价过程设计的可行性，以大亚湾核电站一期工程为例，进行实证算例分析。大亚湾核电站是我国大陆首座大型商用核电站，也是核电央企现代企业制度的首个成功实践单位。其一期工程的两台百万级核电机组自1994年首次并网已稳定运行27年，平均发电负荷因子(1)负荷因子历史数据来源：IEAE Power Reactor Information System-Country Statistics(https://pris.iaea.org/PRIS/CountryStatistics/CountryDetails.aspx?current=CN)。达86.38%，75%WANO(2)WANO指标是全球核电行业通用的指标体系，包含14个单项指标和一个综合指数。其主要量化评价核电厂在核安全、发电管理、维修优化、设备可靠性和工业安全等方面的综合表现。指标达世界卓越水平，运营管理及数据完备性一流，是我国“样板”核电机组，具备研究代表性。因为1号机组在并网之初负荷因子存在异常低值，故仅计算2号机组数据。预测机组现金流的基本假设为：

(1)核电机组所在地区社会、经济环境无重大变化；

(2)核电机组在资产专项计划期间收益权利、收费标准保持不变；

(3)核电机组在资产专项计划期间的经营环境及市场行情无重大变化。

3.1 未来现金流模拟预测

根据上文定价步骤，首先确定售电收入预期净现金流。我国电价受国家管控，相对稳定，发电量是影响核电收益的主要因素，机组负荷因子决定实际发电量。对大亚湾2号机组负荷因子历史数据进行分析发现，负荷因子系数维持在稳定的范围内波动，对其进行单因素正态检验，由于样本数为27，小于50，额外对样本进行了Shapiro-Wilk检验，结果如表1所示，显著通过正态性检验。其中，正态Q-Q图如图1所示，散点均匀分布在45°斜线两侧，故该2号机组负荷因子符合正态分布，经计算在算例中设定σt～N(86.3%，8.3%)。

图1 负荷因子正态Q-Q图

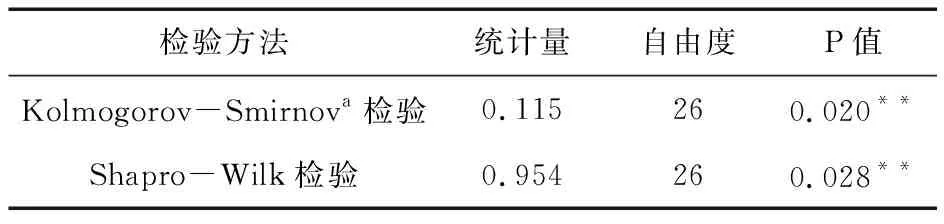
表1 负荷因子单因素正态检验结果

现阶段我国核电采取标杆电价制，此处以核电标杆电价0.43元/kWh作为售电收入单价，机组年运行期限以中电联公布的7 000小时为估算标准。核电初始投资成本主要包括核设备成本、基础建设成本、土地租赁费用、财务成本以及其他业主成本等，算例以中广核披露数据2 222美元/KW[16]作为初始单位建设成本，核电站设计寿命为60年，以剩余服役期40年进行资产折旧。核电站运行燃料费用主要为天然铀成本，铀价格受市场供需及政治因素双重影响，模型中天然铀消耗量以行业平均值20t/GW计算，铀价设定为近3年国际市场均价30美元/磅。乏燃料处理费依据2010年财政部、国家发改委等联合印发的《核电站乏燃料处理处置基金征收使用管理暂行办法》规定，按核电站上网电量征收，征收标准为0.026元/kWh。核电站运维费用按机组现金流入量的8%估算。核电属于重资产行业，建设期资本化财务费用比重大，运营期费用化财务费用占比较高，结合中核集团2018—2020年的3年年报数据(3)年报数据来源：巨潮资讯网(http://www.cninfo.com.cn/new/commonUrl/pageOfSearch?url=disclosure/list/search&lastPage=index)。，此处按机组现金流入量2%比例估算。因核电行业享受增值税先征后退的税收优惠，且土地使用税数额影响不大，故只考虑企业所得税，优惠税率为15%。此外，算例机组建设期(取1993年数据)美元与人民币汇率按3∶1计算，定价期(2021年)汇率为6∶1。将上述影响核电站未来现金流的基础数据汇总，算例机组各项参数指标如表2所示。

表2 基本参数表

根据机组负荷因子σt的分布函数生成随机数，将现金流各参数带入式(1)计算各期净现金流数据，运用Monte Carlo法模拟大亚湾2号机组未来3年售电收益净现金流分布情况，记录数据均值，最小值及10%分位数点。图2为模拟100 000次后的现金流预测数值分布结果。

图2 机组净现金流模拟分布结果

3.2 拟合到期收益率曲线

首先，选取定价日2021年11月30日当月国开债交易数据，获取票面利率、收盘价、付息频率、到期日等信息，根据NSS模型拟合到期收益率曲线，得到基准利率期限结构曲线。其次，确定信用利差。现有研究多使用企业债及公司债交易数据计算利差均值。为真实反映核电行业投资风险状况，通过手工收集现有核电上市企业(核电业务占比80%以上)近3年发行的固定收益类债券信息，因符合要求的核电行业上市公司信用评级均为AAA级，故计算AA+级债券利差时采用非核电企业债及公司债数据。由公式(5)计算利差结果如表3所示，AAA级债券Z-spread均值为1.3% ，AA+级债券Z-spread均值为2.79%。

表3 各评级债券信用利差计算数据表

续表

3.3 产品信用增级、总体发债规模与票面利率的确定

根据基础资产未来现金流可靠性程度进行产品分级，并设计顺序偿付结构进行内部信用增级：优先级证券对标AAA级债券即期收益率，对应偿付现金流为预测现金流最小值，所有模拟值均大于该数值，现金流保障程度最高；次优级证券对标AA+级债券即期收益率，发行规模为模拟净现金流90%置信区间下限现值和优先级产品发行规模之差。基于瀑布式偿还结构，AAA级信用等级最高，优先享有获得全部偿付现金流的权利，AA+仅次于AAA级，次级产品由发起人自持，不参与市场交易，用以为优先级和中间级证券产品提供信用支持。当较高等级证券完成本期现金偿付后，剩余现金流全额分配给次级债券，故发行人自持的次级债券为总体发行规模减去各优先级证券融资规模。表4和表5分别为优先级和次优级产品发行规模计算结果。

假定除次级证券外均为平价发行，每年付息一次，根据公式(6)计算可得未来三年净现金流均值现值(NAV)为66.12 亿元。假定证券发行费用、专项计划管理人及托管人的佣金支出费率为2%，故总体资金募集额为64.80亿元。由公式(7)计算得AAA级证券票面利率为3.44%，AA+级为4.92%。证券化市场现有收费收益权产品利率集中在3%至5.5%。该算例结果基本符合同类证券化产品平均价格水平。因此，该定价思路具有一定可行性，能够对核电收益权资产证券化进行客观合理定价。表6为大亚湾一期2号机组收益权资产证券化分级产品利率和发行规模信息表。

表4 优先级证券化产品发行规模

表5 次优级证券化产品发行规模

表6 大亚湾一期2号机组收益权证券化产品发行情况

4 结论与建议

4.1 研究结论

核电证券化定价准确与否直接影响证券化成败，因此合理定价是实施资产证券化过程中最关键的环节，也是极为困难的一环。通过比较分析证券化定价方法特点及核电资产的适用性，结合售电收益权现金流特征和行业特点提出三步法定价思路。以大亚湾核电站一期2号机组为例，建立静态利差模型并结合Monte Carlo算法测算单一机组核电收益权的理论价格和融资规模，得到如下结论。

第一，静态利差法更适合现阶段核电收益权资产定价。核电收益权资产现金流保障程度极高，现有收费收益权类产品发行书约定的提前偿付权实质为增信措施，并不构成实质期权。因此，设计定价思路时应重点考虑收益现金流变化、利率期限结构、风险溢价利差等因素的影响。通过对比市场同类产品价格和实证结果可知，静态利差法能对我国核电收益权进行客观合理的定价。

第二，负荷因子是定价现金流的关键控制点。通过算例机组负荷因子的正态性检验及售电现金流Monte Carlo模拟可知，核电站现金流呈“尖峰厚尾”形态，机组负荷因子波动率大小决定现金净流量模拟均值与极端低值，进而影响资产证券化价格。

第三，无风险利率拟合时选择国开债等政策性金融债能够消除国债利率内含的免税效应影响。国开行等政策性银行被标准普尔、穆迪等多家知名评级机构认定信用评级与主权国家信用评级一致；同时我国政策性金融债收益不享受任何企业所得税税收优惠，实证分析中NSS模型拟合效果也较好，故发行占比最高的国开债利率更适合作为基准利率分析样本。

第四，实施售电收益权资产证券化将有效缓解核电建设资金缺口。实证算例中一台百万级核电机组三年售电收益证券化融资规模达64.8亿，目前我国在运核电机组超50台，充分利用行业存量资产，以三年期收益权计算总融资额将超3 000亿元。鉴于我国减排压力及能源低碳转型需求，核电项目核准持续加速，资金问题将更加严峻，证券化融资方法将在很大程度上缓解核电建设资金缺口问题。

4.2 启示建议

通过上述定价研究，现针对证券化定价优化提出以下三点建议。

第一，建立政府担保机制，提高核电资产证券化价格抗风险能力。在未发生重大核事故的前提下，核电收益权资产融资价值稳定。虽然重大核事故实际发生概率极低，但潜在证券购买人对事故风险预期较高。考虑到核电行业重资产特征和政治敏感性，企业不具备担保能力，建议尝试由中央或地方政府通过差额补足、重大风险兜底等形式对核电资产收益进行事故风险担保，提升投资者信心的同时降低证券价格风险溢价成本。

第二，重视数据积累，多方合作加快推进构建行业资产定价参考数据库。鉴于核电定价参考数据缺失现状，为提升证券化基础数据完备性，金融监管机构方应明确规范披露主体、内容及频率，强化资产证券化信息披露制度的执行与完善。数据完备性建设方面，建议行业协会、金融机构、核电企业三方协作，推动实现传统数据库的分布式转变，逐步建立以信用等级、行业资产分类的定价基础信息数据库，完善市场定价基础，提高定价结果的准确性与公允性。

第三，进一步探究非系统性风险量化，设计风险导向的动态产品价格机制。风险量化方面主要研究了异质性信用等级风险溢价，总体局限宏观层面的系统风险，后续定价模型优化应进一步拓展考量证券化发起人内生性风险，如流动性风险、违约与早偿风险；针对行业风险如核安全风险，核政策风险、核燃料价格波动风险等非系统性风险，可考虑设计基于基础收益的固定利率叠加风险浮动利率的动态产品价格机制。